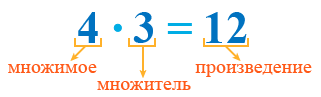Как узнать второй множитель
Нахождение неизвестного слагаемого, множителя, и т.п., правила, примеры, решения
Долгий путь наработки навыков решения уравнений начинается с решения самых первых и относительно простых уравнений. Под такими уравнениями мы подразумеваем уравнения, в левой части которых находится сумма, разность, произведение или частное двух чисел, одно из которых неизвестно, а в правой части стоит число. То есть, эти уравнения содержат неизвестное слагаемое, уменьшаемое, вычитаемое, множитель, делимое или делитель. О решении таких уравнений и пойдет речь в этой статье.
Здесь мы приведем правила, позволяющие находить неизвестное слагаемое, множитель и т.п. Причем будем сразу рассматривать применение этих правил на практике, решая характерные уравнения.
Навигация по странице.
Чтобы найти неизвестное слагаемое, надо…
Женя с Колей решили покушать яблок, для чего начали их сшибать с яблони. Женя добыл 3 яблока, а в конце процесса у мальчиков оказалось 8 яблок. Сколько яблок сшиб Коля?
Для этого существует следующее правило: чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
Озвученное правило позволяет по одному известному слагаемому и известной сумме определить другое неизвестное слагаемое. При этом не имеет значения, какое из слагаемых неизвестно, первое или второе. Рассмотрим его применение на примере.
Чтобы убедиться в правильности полученного ответа, желательно сделать проверку. Для этого полученный корень уравнения надо подставить в исходное уравнение и посмотреть, дает ли это верное числовое равенство.
Как найти неизвестное уменьшаемое, вычитаемое?
Связь между сложением и вычитанием чисел, про которую мы уже упоминали в предыдущем пункте, позволяет получить правило нахождения неизвестного уменьшаемого через известное вычитаемое и разность, а также правило нахождения неизвестного вычитаемого через известное уменьшаемое и разность. Будем формулировать их по очереди, и сразу приводить решение соответствующих уравнений.
Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Можно переходить к нахождению неизвестного вычитаемого. Оно находится с помощью сложения по следующему правилу: чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
И прежде чем переходить к следующему правилу заметим, что в 6 классе рассматривается правило решения уравнений, которое позволяет выполнять перенос любого слагаемого из одной части уравнения в другую с противоположным знаком. Так вот все рассмотренные выше правила нахождения неизвестного слагаемого, уменьшаемого и вычитаемого с ним полностью согласованы.
Чтобы найти неизвестный множитель, надо…
Желательно еще сделать проверку результата: подставляем в исходное уравнение вместо буквы найденное значение, получаем 4·3=12 – верное числовое равенство, поэтому мы верно нашли значение неизвестного множителя.
И еще один момент: действуя по изученному правилу, мы фактически выполняем деление обеих частей уравнения на отличный от нуля известный множитель. В 6 классе будет сказано, что обе части уравнения можно умножать и делить на одно и то же отличное от нуля число, это не влияет на корни уравнения.
Как найти неизвестное делимое, делитель?
В рамках нашей темы осталось разобраться, как найти неизвестное делимое при известном делителе и частном, а также как найти неизвестный делитель при известном делимом и частном. Ответить на эти вопросы позволяет уже упомянутая в предыдущем пункте связь между умножением и делением.
Чтобы найти неизвестное делимое, надо частное умножить на делитель.
Заметим, что разобранное правило можно трактовать как умножение обеих частей уравнения на известный делитель. Такое преобразование не влияет на корни уравнения.
Переходим к правилу нахождения неизвестного делителя: чтобы найти неизвестный делитель, надо делимое разделить на частное.
Проверим этот результат для надежности: 18:6=3 – верное числовое равенство, следовательно, корень уравнения найден верно.
Совместное использование правил
Последовательное применение правил нахождения неизвестного слагаемого, уменьшаемого, вычитаемого, множителя, делимого и делителя позволяет решать и уравнения с единственной переменной более сложного вида. Разберемся с этим на примере.
Как найти множитель
Как найти неизвестный множитель? Способ первый — применить правило нахождения неизвестного множителя:
Как быть, если нужно решить уравнение, а правило позабылось? В этом случае можно придумать пример на умножение, чтобы разобраться с его помощью, что следует сделать, чтобы найти множитель, и так же найти неизвестный множитель в своем уравнении.
Как найти неизвестный первый множитель — 2? Надо 6 разделить на 3. Вывод: чтобы найти первый множитель, нужно произведение разделить на второй множитель.
Как найти второй множитель — 3? Надо 6 разделить на 2. Значит, чтобы найти второй множитель, нужно произведение разделить на первый множитель.
Так как от перемены мест множителей произведение не меняется, для нахождения неизвестного множителя порядок множителей можно не учитывать.
Рассмотрим на примерах, как найти неизвестный множитель.
1)
| 8 | · | x | = | 72 |
| 1мн. | 2мн. | пр. |
Чтобы найти неизвестный множитель, делим произведение на известный множитель:
| y | · | 10 | = | 280 |
| 1мн. | 2мн. | пр. |
Чтобы найти множитель, надо произведение разделить на известный множитель:
Более сложные примеры, в которых умножение — только одно из действий, мы рассмотрим позже.
Поиск множителей числа на определенном интервале чисел
Алгоритм поиска множителей числа, то есть представление какого либо числа в виде двух других чисел, при умножении которых мы получил непосредственно то число, которое нам нужно. Эта статья не рассказывает о каких либо идеальных/лучших алгоритмов, это своего рода оптимизация перебора чисел, и далеко не стоит по сравнению с тем же методом факторизации Ферма ну или Ро-алгоритмом Полларда.
В чем заключается данный алгоритм?
В первую очередь, берем интервал чисел, который представляем в виде двух целых чисел, это конец интервала и его начало. Так же нам нужно число, с которого мы хотим получить множители на интервале.
Теперь перейдем к самому алгоритму. Чтобы не идти вглубь математики, мы будем рассматривать этот метод исключительно на человеческом языке.
Для начала, нам нужны сами пределы интервала, их мы пусть присвоим ‘x‘ и ‘y‘, начало и конец соответственно.
Теперь мы, умножаем эти два числа: z = x*y, и если число, которое мы получили, будет меньше, чем число которое мы планируем факторизовать, то прибавляем к ‘x‘ — единицу(1), и снова умножаем: z = (x+1)*y, и так до тех пор, пока мы не получим (z > N), где ‘N‘ — число которое нужно факторизовать.
Если же, число которое мы получили больше N, то:
1. Мы ищем разницу между ‘z‘ и ‘N‘, то есть между числом которое мы получили и число которое мы хотим факторизовать.
2.1. Число, которое мы получили после вычитания(q), делим на число которое символизирует начало интервала(x). После чего, проверяем условие: Если получается число, не целого типа, то множителей не будет, а следовательно мы увеличиваем начальное значение(x) на единицу и продолжаем поиск.
2.2. Если же, число которое мы получили при делении — целого типа, тогда мы: От конца интервала отнимаем число которое мы получили(пусть будет ‘l‘), в следствии чего мы получаем один из множителей, второй же множитель — это ‘x‘.
Есть интервал чисел от 14 к 28, и число которое мы хотим разложить на множители, пусть будет 450.
Для начала нам нужно два числа, это начало и конец интервала, в данном случаи это 14 и 28. Дальше мы согласно алгоритму, эти два числа умножаем и получаем результат:
Число, которое мы получили, меньше чем число, которое нам нужно разложить на множители, то есть 450, тогда мы увеличиваем 14 на единицу, и начинаем все с начала.
Опять же, 420 504-450 = 54
Теперь главная проверка, делим полученное число на 18, получаем результат:
А вот и число целого типа, то есть уже на этом этапе понятно что множители мы нашли, теперь согласно пункту 2.2 нам нужно их точно высчитать:
По такому принципу работает этот алгоритм, на самом деле он далеко не хороший, так как во первых при очень большом интервале поиск множителей может идти довольно долго, и вообще я без документации, без сторонней помощи вышел на него, возможно он уже и был где-то описан, но этот алгоритм можно назвать «ради идеи», ну и чтобы не деградировать.
Of course, winning is one of the main goals, but we must remember that there is no ideal, and if you think that you have achieved this ideal — you have lost.
Умножение натуральных чисел
Умножение — это арифметическое действие, с помощью которого находят сумму одинаковых слагаемых.
Пример. Во дворе посадили 3 ряда ёлок, по 4 ёлки в каждом ряду. Сколько ёлок посадили во дворе?
Чтобы ответить на этот вопрос, надо найти сумму 3 слагаемых, каждое из которых равно 4.
Складывая 3 раза по 4 ёлки, мы получим общее количество ёлок во всех трёх рядах.
Умножить – значит повторить одно число слагаемым столько раз, сколько в другом содержится единиц.
Для записи умножения используется знак х (косой крест) или · (точка), который ставится между числами. Например:
Эта запись означает, что 4 надо умножить на 3. Справа от записи умножения ставится знак = (равно), после которого записывается полученный результат:
Умножение – это краткая запись сложения одинаковых слагаемых.
Пример. Умножить 6 на 5 — это значит найти сумму пяти слагаемых, каждое из которых равно шести:
Сократим запись, заменив сложение на умножение:
Оба выражения равны:
6 + 6 + 6 + 6 + 6 = 6 · 5 = 30,
но для краткости записей лучше всегда использовать умножение, когда число одинаковых слагаемых больше двух.
Множимое, множитель и произведение
Множимое — это число, которое умножают. Множитель — это число, на которое умножают. Например, в записи:
4 — это множимое, 3 — множитель. Множимое является числом, которое выступает в качестве слагаемого. Множитель — это число, которое указывает количество одинаковых слагаемых.
Произведение — это число, которое получается в результате умножения. Например, в записи:
12 — это произведение. При этом сама запись 4 · 3 тоже называется произведением.
Множимое и множитель иначе называются множителями или сомножителями.
Проверка умножения
Умножение двух чисел можно проверить делением, для этого произведение делят на один из сомножителей, если частное окажется равно другому сомножителю, то умножение выполнено верно.
Умножение
В этом разделе познакомимся с умножением и узнаем, что сложение одинаковых слагаемых можно заменить умножением.
Например, 6 + 6 + 6 + 6 = 24 можно записать по-другому: 6 • 4 = 24
Смысл действия умножения состоит в том, что при умножении находится сумма одинаковых слагаемых.
Первое число при умножении показывает, какое слагаемое повторяют несколько раз.
Второе число при умножении показывает, сколько раз повторяют это слагаемое.
Результат умножения показывает, какое число получается.
6 • 4 значит, что число 6 повторяют 4 раза: 6 + 6 + 6 + 6 = 24
Числа при умножении
Результат умножения, или Произведение
Чтение числовых выражений
Этот пример можно прочитать по-разному.
Умножение на 1
4 • 1 = 4, потому что это значит, что число 4 повторяют только 1 раз.
23 • 1 = 23, потому что это значит, что число 23 повторяют только 1 раз.
Умножение на 0
8 • 0 = 0, потому что это значит, что число 8 повторяют 0 раз.
26 • 0 = 0, потому что это значит, что число 26 повторяют 0 раз.
Умножение на 10
8 • 10 = 80, потому что число 8 повторяют 10 раз.
15 • 10 = 150, потому что число 15 повторяют 10 раз.
Связь деления и умножения
8 • 3 = 24, потому что 8 повторяют 3 раза.
24 : 3 = 8, потому что в 24 по 3 содержится 8 раз.
24 : 8 = 3, потому что в 24 по 8 содержится 3 раза.
В несколько раз больше
Решим задачу:
В магазине было 2 лисички, а котят в 4 раза больше. Сколько было котят?
Это значит, что котят было 4 раза по 2.
Заменяем сложение умножением и получаем:
Во сколько раз больше? Во сколько раз меньше?
Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?
Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?
Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.
Поделись с друзьями в социальных сетях: