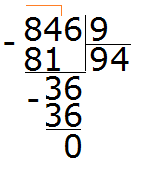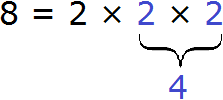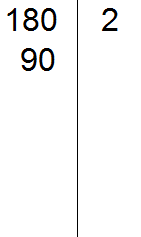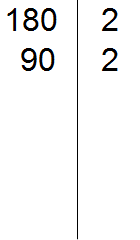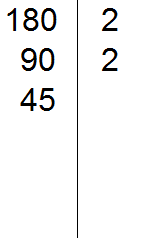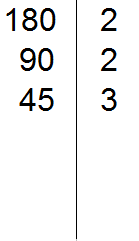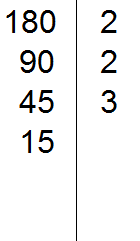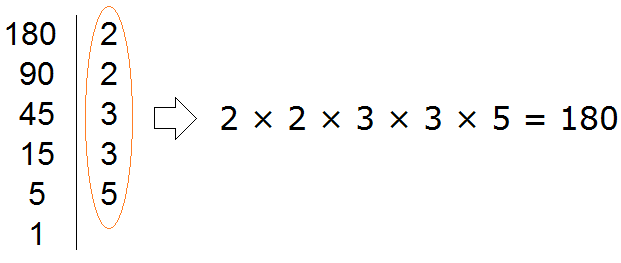Как узнать кратность числа
Делитель и кратное в математике
Что такое делители и кратные числа
Деление — математическое действие, которое определяет, сколько раз одно число содержится в другом. Обратной операцией является умножение.
Выделяют следующие компоненты деления:
Делимое — число, которое делят на несколько частей.
Делитель — число, которое показывает, на сколько частей нужно разделить делимое.
Частное — число, которое является результатом деления.
Умножение частного на делитель дает делимое.
Чтобы получить делитель, нужно делимое разделить на частное.
Д е л и м о е = ч а с т н о е * д е л и т е л ь Д е л и т е л ь = д е л и м о е / ч а с т н о е
Например, нужно поровну разделить 16 мандаринов между двумя детьми. Для этого 16:2=8. Таким образом, каждый ребенок получит по 8 мандаринов.
16 в этом примере является делимым, 2 — делителем, 8 — частным. Шестнадцать поделили на две части, по восемь в каждой. Или восемь содержится в 16 два раза. Или 2 содержится в 16 восемь раз. Деление прошло без остатка — нацело. Тогда число 2 является делителем числа 16.
Делителем числа a называется такое число b, на которое a делится нацело.
Например, 9 : 4 = 2 (остаток 5 ).
В примере 9 — делимое, 4 — делитель, 2 — неполное частное, 5 — остаток.
Остаток от деления — число, которое меньше делителя. Образуется при делении с остатком. Значит, в примере 9 : 4 = 2 (остаток 5 ) — число 4 не является делителем числа 9.
Задание: найдите такую пару делителей числа 144, если один из делителей равен 2.
Пусть неизвестный делитель равен x. Чтобы найти еще один делитель, если какой-то известен, нужно данное нам число разделить на известный делитель.
Тогда представим решение данной задачи в виде уравнения:
72 — целое число, без остатка.
Произведение делителей должно дать в результате 144:
72 * 2 = 144 — верно, значит, 72 — корень уравнения и делитель 144.
Ответ: числа 2 и 72 — делители 144.
Число называют кратным, если оно делится на данное число нацело, без остатка.
Например, 15:3 нацело.
Тогда число 15 является кратным 3.
Слово «кратно» синонимично слову «делится».
Фразу «15 кратно 3» можно в уме заменить на «15 делится на 3 нацело».
Основные понятия и определения
Делитель — это число, на которое данное число делится нацело. Делитель всегда меньше или равен числу.
Делится нацело = без остатка.
Наименьшим делителем любого числа является единица.
Наибольшим делителем числа является само число.
Делителем нуля будет любое число, но сам 0 делителем не будет.
При делении нуля на любое число получаем 0. А делить на ноль нельзя.
У единицы только один делитель — единица.
Другие числа, кроме 1, имеют не меньше двух делителей.
Кратное — число, которое делится на данное число нацело. Всегда больше или равно числу.
Наименьшее кратное числа является равным самому числу.
Наибольшее кратное подобрать нельзя, потому что ряд натуральных чисел бесконечен. У любого натурального числа бесконечное множество кратных.
Ноль является кратным для любого числа. При умножении на ноль всегда получается ноль.
Когда одно число делится нацело на другое, то первое число — кратное второго, а второе — делитель первого.
Чем отличаются друг от друга, как найти
Делитель отличается от кратного тем, что:
Чтобы найти делители числа, нужно данное число разложить на множители.
Разложить на множители — представить число в виде произведения целых чисел.
Чтобы проверить, является ли одно число делителем другого, нужно разделить число на данное нам.
Для нахождения кратного числа заданному числу, нужно это число последовательно умножать на натуральные числа. Каждое полученное число будет кратно — будет делиться — заданному.
Делители и кратные связаны между собой. Например, делителем числа 15 является 3 и число, кратное 3, равно 15.
Примеры решения задач
Необходимо найти делители числа 14.
Решить задание можно двумя способами.
Последовательно делим 14 на натуральные числа от 1 до 14. Помним, что делитель всегда меньше или равен заданному числу.
Выбираем такие числа в качестве делителя, при делении на которые мы не получили остаток: 1, 2, 7, 14.
Ответ: делители числа 14: 1, 2, 7, 14.
Представим 14 в виде произведения чисел:
Делителями будут множители, так как можем разделить 14 нацело на каждый из них.
Ответ: делители 14: 1, 2, 7, 14.
Найдите три числа, кратных 7.
Чтобы найти число, кратное данному, нужно это число умножить на любое натуральное число.
7 * 1 = 7 — семь кратно семи;
7 * 2 = 14 — 14 кратно 7;
7 * 3 = 21 — 21 кратно 7.
Ответ: числа, кратные 7: 7, 14, 21.
Самостоятельно проверьте, 225 кратно 3 или нет.
Чтобы проверить, кратно ли одно число другому, нужно разделить числа друг на друга.
75 — целое число, при делении нет остатка. Тогда 225 кратно 3.
Найдите любое число, делителями которого являются числа 7 и 8.
Самый простой способ, если в задании не оговорены еще какие-либо условия, просто перемножить эти делители:
Признаки делимости на 2, 3, 4, 5, 6, 9, 10, 11
Признак делимости на 2
Число делится на 2 тогда и только тогда, когда его последняя цифра делится на 2, то есть является чётной.
2, 8, 16, 24, 66, 150 — делятся на 2, так как последняя цифра этих чисел четная;
3, 7, 19, 35, 77, 453 — не делятся на 2, так как последняя цифра этих чисел нечетная.
Признак делимости на 3
Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3.
75 — делится на 3, так как 7+5=12, и число 12 делится на 3 (12:3=4);
471 — делится на 3, так как 4+7+1=12, и число 12 делится на 3 (12:3=4);
532 — не делится на 3, так как 5+3+2=10, а число 10 не делится на 3 (10:3=3 1 3 ).
Признак делимости на 4
Число делится на 4 тогда и только тогда, когда две его последние цифры составляют число, которое делится на 4. Двузначное число делится на 4 тогда и только тогда, когда удвоенное число десятков, сложенное с числом единиц делится на 4.
4576 — делится на 4, так как число 76 делится на 4 (7·2+6=20, 20:4=5);
9634 — не делится на 4, так как число 34 не делится на 4 (3·2+4=10, 10:4=2 1 2 ).
Признак делимости на 5
Число делится на 5 тогда, когда последняя цифра делится на 5, т.е. если она 0 или 5.
375, 5680, 233575 — делятся на 5, так как их последняя цифра равна 0 или 5;
9634, 452, 389753 — не делятся на 5, так как их последняя цифра не равна 0 или 5.
Признак делимости на 6
Число делится на 6 тогда и только тогда, когда оно делится и на 2, и на 3, то есть если оно четное и сумма его цифр делится на 3.
462 — делятся на 6, по признаку делимости на 2 оно делится на 2 (последняя цифра 2 делится на 2), по признаку делимости на 3 оно делится на 3 (сумма цифр числа делится на 3: 4+6+2=12, 12:3=4);
3456 — делятся на 6, по признаку делимости на 2 оно делится на 2 (последняя цифра 6 делится на 2), по признаку делимости на 3 оно делится на 3 (сумма цифр числа делится на 3: 3+4+5+6=18, 18:3=6);
24642 — делятся на 6, по признаку делимости на 2 оно делится на 2 (последняя цифра 2 делится на 2), по признаку делимости на 3 оно делится на 3 (сумма цифр числа делится на 3: 2+4+6+4+2=18, 18:3=6);
861 — не делятся на 6, так как по признаку делимости оно не делится на 2;
3458 — не делятся на 6, так как по признаку делимости оно не делится на 3;
34681 — не делятся на 6, так как по признаку делимости оно не делится на 2.
Признак делимости на 9
Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9.
468, 4788, 69759 — делятся на 9, так как сумма их цифр делится на девять (4+6+8=18, 4+7+8+8=27, 6+9+7+5+9=36);
861, 3458, 34681 — не делятся на 9, так как сумма их цифр не делится на девять (8+6+1=15, 3+4+5+8=20, 3+4+6+8+1=22).
Признак делимости на 10
Число делится на 10 тогда и только тогда, когда оно оканчивается на нoль.
460, 24000, 1245464570 — делятся на 10, так как последняя цифра этих чисел равна нулю;
234, 25048, 1230000003 — не делятся на 10, так как последняя цифра этих чисел не равна нулю.
Признак делимости на 11
Число делится на 11 если сумма цифр стоящих на четных местах равна сумме цифр стоящих на нечетных местах или отличается от нее на число кратное 11.
Признаки делимости чисел
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Что такое «признак делимости»
Признак делимости числа — это такая особенность числа, которая еще до выполнения деления позволяет определить, кратно ли число делителю.
Истинный путь джедая, чтобы зря не пыхтеть над числами, которые в конечном итоге не делятся.
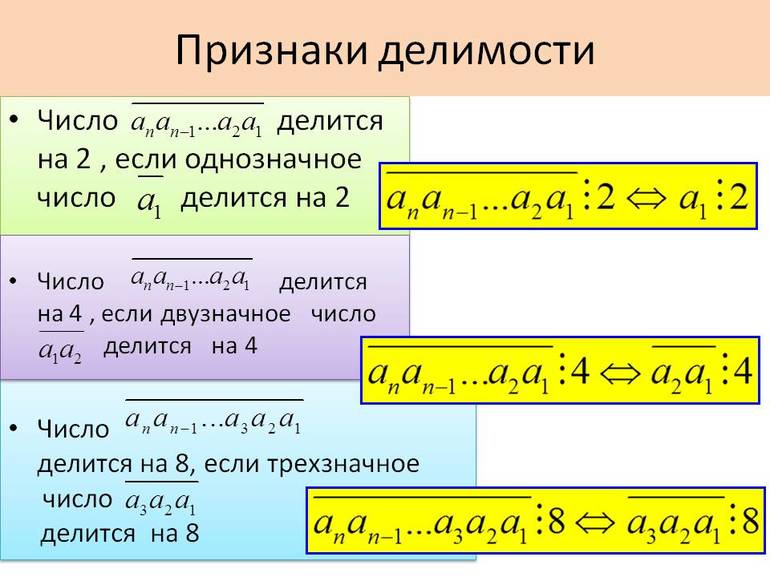
Однозначные, двузначные и трехзначные числа
Однозначное число — это такое число, в составе которого один знак (одна цифра). Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Двузначные числа — такие, в составе которых два знака (две цифры). Цифры могут повторяться или быть различными.
Трехзначные числа — числа, в составе которых три знака (три цифры).
Чётные и нечётные числа
Число называют четным тогда, когда оно делится на два без остатка. А нечетные числа — те, что на два без остатка не делятся. Все просто!
Признаки делимости чисел
Признак делимости на 2. Сразу можно сказать, что число делится на 2, если последняя цифра четная.
Признак делимости на 3. Сумма цифр числа должна делиться на 3.
Признаки делимости на 4. Число делится на 4, если две последние цифры — 0 или если они образуют цифру, которая делится на 4.
Признаки делимости на 5. Число делится на 5, если заканчивается на 0 или 5.
Признак делимости на 6. На 6 делятся те числа, которые могут одновременно делится на 2 и на 3.
Признаки делимости на 8. Число делится на 8, если три последних цифры — 0 или если они образуют число, которое делится на 8.
Признак делимости на 9. Число делится на 9, если сумма цифр делится на 9.
Признаки делимости на 10, 100. Числа, которые заканчиваются на 0, 00, 000 делятся на 10, 100, 1000 и так далее.
Дроби с кратными от 1 до 5
На единицу делится любое целое число.
Самым простым правилом является делимость на число два: если натуральное число оканчивается на четную цифру, то оно кратно двум. Если в конце стоит нечетная цифра, какими являются 1, 3, 5, 7, 9, то число на два не делится. То есть чтобы поделить многозначное число на два, в конце числа должна стоять одна из таких цифр: 2, 4, 6, 8, 0.
Пример: 6942 является четным, поскольку в конце четная цифра, поэтому оно кратно двум; число 19678456 также кратно двум, так как в конце стоит четная цифра 6. А вот число 6796345 не делится на 2, поскольку оно нечетное. Также нельзя получить ответ без остатка с такой суммы, как 398573 по этой же причине.
Деление на три имеет свое правило: нужно сложить все цифры, а затем проверить, делится ли сумма на три. Если да, то и данность разделится на три. Если нет, значит, не делится.
Например, возьмем 3576. Складываем 3+5+7+6=21. Полученную сумму 21 делим на три, получается семь. Значит, оно кратно трем без остатка. Проведем разложение шестизначного номера 353388. Оно раскладывается на три, поскольку сумма равна тридцати (3+5+3+3+8+8=30). Еще возьмем, например, 5819. Складываем: 5+8+1+9=23, полученная сумма не делится на три без остатка. Также и 2947 невозможно разделить, поскольку остаются тройки.
Правило делимости на четыре звучит так: если две последние цифры номера кратны четырем либо оно в конце имеет два нуля, то отношение получится без остатка.
Например, 1000 делится на четыре, поскольку в конце 00. Делится также и 3824, так как в конце 24, которое кратно этому делителю. А вот 2986 не делится на четыре, так как 86 не кратно четырем, и 29087 тоже не может остаться целым, поскольку с 87 нельзя произвести расчета. Еще пример: четырехзначный номер 2648 можно разделить на этот делитель, так как 48:4=12.
Довольно простым правилом является делимость на пять. Частное получается без остатка, если в конце заданного числа стоит 5 или 0. Если оно не заканчивается одной из этих цифр, то при делении возникнет остаток.
Проверим правило, взяв пятизначное число 45765. Оно кратно пяти без остатка, так как заканчивается на пять. Также 45030 можно разделить, поскольку в конце ноль. А вот четырехзначное число 4321 без остатка не делится.
Свойства делителей от 6 до 10
Составное шесть состоит из произведения двух последовательных чисел — 2 и 3. Теория кратности такова: число 6 составное, поэтому необходимо, чтобы одновременно действовали два правила признака делимости. Нужно, чтобы число было кратно и двум, и трем сразу.
Например, проверке подвергаются трехзначные числа 756 и 168. Они четные, поэтому делятся на два. Теперь нужно сложить 7+5+6=18, становится ясно, что сумма 18 делится на 3. Число 165 при разложении на однозначные цифры с последующим сложением превращается в 12, которое может разделиться на три. Оба числа кратны одновременно 2 и 3, значит, кратны шести.
Определение отношения с делимостью на семь довольно сложное: число делится, если при удвоении последней цифры и полученной разности результат кратен семи или равен нулю.
Пример, трехзначное число 679 кратно 7. (Калькулятор выдал 97). Узнать можно так:
Из примера видно, что удвоилось последнее число, затем получена разность, после чего — отношение-доказательство.
В классе было дано задание доказать, что число 497 делится на семь. Порядок решения:
Найти признак делимости на 8 очень легко. Формулировка закона такова: последние три цифры должны быть 000 или 888. Легко можно произвести вычисления с 789000: оно делится на 8, так как оканчивается на 000. Множество 289673888 тоже кратно 8, поскольку заканчивается на 888.
Свойство при делителе 9 похоже на правило с 3. Формула делимости на 9 довольно простая: сумма цифр должна быть кратна девяти. Маленький пример: из 46980 возможно получить целое, 4+6+9+8+0= 27. Получившаяся сумма кратна 9. Еще одно задание: найти отношение с использованием признака кратности 9 при делимом 29565. Рассуждение: 2+9+5+6+5=27. Полученная сумма может разделиться на девять.
Разрядные единицы
Любое число можно разделить на разрядную единицу, если у него одинаковое или большее количество нулей в конце. Например, 5790 можно поделить на 10, так как в конце один ноль. Еще примеры:
Невозможно разделить 128700 на 1000, так как у разрядной единицы нулей больше, а также 237480 на 100 и другие подобные.
Делители от 11 и выше
Чтобы получилось деление на 11, необходимо сложить четные по счету номера, а затем нечетные, затем произвести вычитание. Если в процессе вычислений получился ноль или одиннадцать, то остатка не будет.
Онлайн-задание с ответом: 7535, 74019 и 50486.
Нечетные в первом случае 7 и 3, четные 5 и 5. Считаем:
Четные во втором примере 4 и 1, нечетные — 7, 0, 9. Вычисление:
В третьем примере нечетные 5, 4, 6, четные 0 и 8. Решаем:
Ответ: в первом и втором примере десятых, сотых, тысячных и так далее не останется, а в третьем — останется.
Чтобы разделить на двузначный делитель 12, нужно произвести общие вычисления, характерные для делителей 3 и 4 одновременно. К примеру, 900 и 3432. Сначала следует разложить на слагаемые 9+0+0=9, значит, можно поделить на 3. В конце стоит два нуля — можно делить на 4. Проверка: 900:12=75. Первая часть задания решена, теперь делаем вторую: 3+4+3+2=12, 12:3=4. Таким образом проверяется кратность трем. Теперь четырем: в конце стоит 32, что указывает на кратность 4, значит, остатка не будет. Таким образом, оба примера кратны 12.
Дробь, кратная 13, разрешится без остатка, если последнюю цифру умножить на 4, после чего сложить число и последнюю цифру. Если полученная сумма кратна 13 или равно 0, то деление получится.
Например, 6942:
Еще пример — 754:
Признак делимости на составное число
Если делитель составной, необходимо его разложить на простые множители, которые не имеют общих кратных, кроме единицы. Пример: 15 раскладывается на 3 и 5. Любое неизвестное кратно 15, если одновременно кратно трем и пяти.
Также и с другим составным: 18 раскладывается на 2 и 9. Нельзя брать множители 3 и 6, так как они не простые, у них общее кратное 3. Например, 456 кратно трем, проверка: 4+5+6=15, также кратно 6 (при разложении на 2 и 3). Однако калькулятор выводит запятую. Если взять множители 2 и 9, будет видно, что двум — кратно, а девяти — нет, ведь сумма равна 15, которая не кратна 9.
Таблица кратных от 2 до 10
Для удобства школьникам и их родителям предлагается таблица признаков делимости чисел от 2 до 10. Она наглядно и кратко демонстрирует всю вышеизложенную теоретическую часть:
| Делимость на: | Признак числа: |
| 2 | Оканчивается четной цифрой: 0, 2, 4,6, 8 |
| 3 | Сумма цифр, их которой оно состоит, делится на 3 |
| 4 | Две последние цифры делятся на 4 |
| 5 | Окончание на 5 или 0 |
| 6 | Одновременная кратность 2 и 3 |
| 8 | Три последние цифры кратны 8 |
| 9 | Сумма цифр кратна 3 |
| 10 | Окончание равно нулю |
Вышеизложенное доказывает, что к любому натуральному числу можно подобрать простой или составной признак кратности. На практике выходит, что чем больше число, тем сложнее его признак. Часто не хочется тратить время на проверку делимости, ведь за этот промежуток уже можно выполнить само деление. Поэтому любой школьник может воспользоваться простейшими признаками делимости.
Делители и кратные
В данном уроке мы рассмотрим такие понятия как делители и кратные.
Что такое делитель?
Мы знаем, что делитель это число, показывающее на сколько частей нужно разделить делимое. Например, в выражении 8 : 2 = 4, делителем является число 2. Это число показывает на сколько частей нужно разделить число 8. После разделения получается ответ 4. Как видно из примера, число 8 делится на число 2 без остатка. Говорят, что число 2 является делителем числа 8.
Пример 1. Число 2 является делителем числа 8, поскольку 8 делится на 2 без остатка:
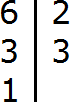
Пример 2. Число 3 является делителем числа 9, поскольку 9 делится на 3 без остатка:
Пример 3. Число 4 не является делителем числа 10 поскольку 10 не делится на 4 без остатка:
10 : 4 = 2 (2 в остатке)
Определение. Делителем числа а называется число, на которое число а делится без остатка.
Делителем числа 12 называется число, на которое 12 делится без остатка.
Попробуем перечислить эти числа:
Все эти числа являются делителями числа 12, поскольку число 12 делится на них без остатка. Покажем это:
12 : 1 = 12
12 : 2 = 6
12 : 3 = 4
12 : 4 = 3
12 : 6 = 2
12 : 12 = 1
Кратные числа
Если какое-нибудь число без остатка разделилось на другое, то его называют кратным этого числа. Например, 6 без остатка делится на 3. Поэтому 6 является кратным числа 3
Определение. Кратным числа а называется число, которое делится без остатка на а.
Кратным числа 5 называется число, которое делится без остатка на 5 .
У любого числа бесконечно много кратных. Например, первыми кратными числа 5, являются числа 5, 10, 15, 20, 25. Все они кратны 5, поскольку делятся на 5 без остатка:
5 : 5 = 1
10 : 5 = 2
15 : 5 = 3
20 : 5 = 4
25 : 5 = 5
Признаки делимости чисел
Признаки делимости чисел используются для того, чтобы ускорить процесс деления чисел. Существует множество признаков делимости и других интересных алгоритмов, значительно ускоряющих решение и освобождающих от излишней волокиты. Рассмотрим наиболее популярные из них.
Признак делимости на 10
Любое число, которое оканчивается нулем, делится без остатка на 10. Чтобы получить частное, достаточно отбросить цифру 0 в делимом.
Например, 380 : 10 = 38. Мы просто отбросили последний ноль в числе 380.
В случае, если мы имеем выражение такого вида 385 : 10, то получится 38 и 5 в остатке, поскольку 380 : 10 = 38, а пятерка это остаток, который не разделился.
Таким образом, если число оканчивается цифрой 0, то оно делится без остатка на 10. Если же оно оканчивается другой цифрой, то оно не делится без остатка на 10. Остаток в этом случае равен последней цифре числа. Действительно, в примере 385 : 10 = 38 (5 в остатке), остаток равен последней цифре в числе 385, то есть пятерке.
Признак делимости на 5 и на 2
Любое число, которое оканчивается нулем, делится без остатка и на 5, и на 2.
Признак делимости на 5
Если число оканчивается цифрой 0 или 5, то оно делится без остатка на 5.
Признак делимости на 3
Число делится на 3, если сумма цифр этого числа делится на 3. Например, рассмотрим число 27, сумма его цифр 2 + 7 = 9. Девять, как мы знаем делится на 3, значит и 27 делится на 3:
Признак делимости на 9
Число делится на 9, если сумма его цифр делится на 9. Например, рассмотрим число 18. Сумма его цифр 1 + 8 = 9. Девять делится на девять, значит и 18 делится на 9
Рассмотрим число 846. Сумма его цифр 8 + 4 + 6 = 18. Восемнадцать делится на девять, значит и 846 делится на 9:
Чётные и нечётные числа
Чётным называется число, которое делится без остатка на 2. Например, число 20 является четным, поскольку оно делится без остатка на 2:
Нечётным называется число, если при его делении на 2, остаётся остаток 1. Например число 21 является нечетным, поскольку после его деления на 2 остается остаток 1:
21 : 2 = 10 (1 в остатке)
Как распознать чётное число от нечетного, не выполняя деления на 2? Очень просто. Из однозначных чисел чётными являются числа 0, 2, 4, 6, 8, а нечетными являются 1, 3, 5, 7, 9. Если число оканчивается чётной цифрой, то это число является чётным. Если число оканчивается нечетной цифрой, то это число является нечетным.
Например, число 308 чётно, поскольку оно оканчивается чётной цифрой. Число 1024 тоже четно, поскольку оканчивается четной цифрой.
А числа 305 и 1027 являются нечётными, поскольку они оканчиваются нечётными цифрами.
Простые и составные числа
Простым называется число, которое делится без остатка на единицу и на само себя. Другими словами, имеет только два делителя. Например, число 5 делится без остатка на единицу и на само себя:
Значит, число 5 является простым числом.
Составным же называется число, которое имеет два и более делителя. Например, число 4 составное, поскольку у него два и более делителя: 4, 2 и 1
Значит, число 4 является составным числом.
Разложение составного числа на простые множители
Любое составное число можно разложить на простые множители. Чем-то похожим мы занимались в уроке замены в выражениях. Из этого урока мы узнали, что любое число, входящее в выражение, можно заменить на то же самое, но записанное в другом виде.
Суть разложения числа на простые множители заключается в том, чтобы представить это число в виде произведения нескольких простых множителей.
Разложим число 4 на простые множители. Для этого соберем данное число из других чисел, при этом соединим их знаком умножения (×). Число 4 состоит из чисел 2 и 2. Эти два числа и являются простыми множителями, из которых состоит число 4
Разложим на множители число 6. Число 6 можно собрать из чисел 2 и 3. Эти два числа и являются простыми множителями, из которых состоит число 6
Большие числа раскладываются таким же образом. Сначала их раскладывают на большие множители, затем эти большие множители раскладывают на маленькие. И так до тех пор, пока каждый множитель не станет простым числом.
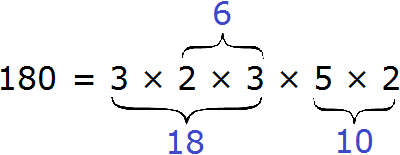
Например, разложим число 180 на простые множители. Число 180 это два множителя 18 и 10
Теперь раскладываем множители 18 и 10 на другие множители:
Теперь раскладываем выделенную синюю шестерку. Это последний большой множитель, который можно разложить на простые множители:
Теперь собираем все простые множители вместе:
На множители можно разложить только составное число. Простое число на множители не раскладывается. Именно поэтому, когда разложение доходит до простых чисел, мы эти простые числа дальше не раскладываем.
Есть и второй способ разложения на простые множители. Он проще и хорошо подходит для больших чисел. Суть этого способа заключается в том, что сначала проводится вертикальная линия. Затем слева от этой линии записываются делимые, а справа — делители, которые впоследствии собирают во множители.
При разложении числа этим способом, используют признаки делимости, такие как: признаки делимости на 2, на 3, на 5 и другие.
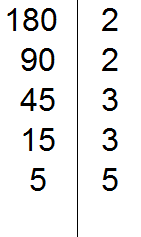
Например, разложим предыдущее число 180 этим способом.
Проводим вертикальную линию и слева записываем первое делимое 180
Теперь применяем признаки делимости. В первую очередь проверяем делится ли 180 на 2. Если делится, то нужно записать эту двойку справа от вертикальной линии.
180 делится на 2, поскольку 180 оканчивается нулём. Записываем двойку справа от вертикальной линии:
Теперь делим 180 на 2 и получаем второе делимое 90. Записываем это делимое слева от вертикальной линии:
Теперь делим 90. Снова применяем признаки делимости. Проверяем делится ли 90 на 2.
90 делится на 2, поскольку 90 оканчивается нулём. Записываем двойку справа от вертикальной линии:
Теперь делим 90 на 2, получаем третье делимое 45. Записываем это делимое слева от вертикальной линии:
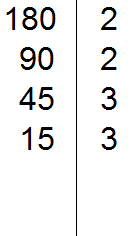
Теперь делим 45. Снова применяем признаки делимости. Проверяем делится ли 45 на 2.
45 на 2 не делится. Тогда проверяем делится ли 45 на 3.
45 делится на 3, поскольку сумма цифр 4 и 5 делится на 3. Записываем тройку справа от вертикальной линии:
Делим 45 на 3, получаем четвёртое делимое 15. Записываем это делимое слева от вертикальной линии:
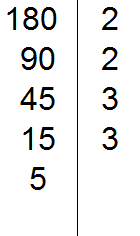
Теперь делим 15. Проверяем делится ли 15 на 2.
15 не делится на 2. Тогда проверяем делится ли 15 на 3.
15 на 3 делится, поскольку сумма цифр 1 и 5 делится на 3. Записываем тройку справа от вертикальной линии:
Делим 15 на 3, получаем пятое делимое 5. Записываем пятёрку слева от вертикальной линии:
Теперь делим 5. Проверяем делится ли 5 на 2.
5 не делится на 2. Тогда проверяем делится ли 5 на 3.
5 не делится на 3. Тогда проверяем делится ли 5 на 5.
5 делится на 5. Записываем эту пятёрку справа от вертикальной линии:
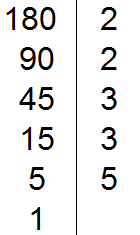
Делим 5 на 5, получаем шестое делимое 1. Записываем эту единицу слева от вертикальной линии:
На этом деление завершается, поскольку мы достигли единицы. Делители, которые записывают справа от вертикальной линии должны быть простыми числами. Поэтому, когда делимое 5 не разделилось на 2, а затем не разделилось на 3, мы попробовали разделить его на 5, не пробуя разделить на 4, поскольку 4 является не простым, а составным числом.
Теперь переписываем в один ряд все делители, которые записаны справа от вертикальной линии. Они и будут разложением числа 180 на простые множители. Желательно записывать их, начиная с самых малых. Это позволяет упорядочить их по возрастанию:
Не расстраивайтесь, если будете испытывать затруднения при разложении чисел на простые множители. Эта тема требует немного практики. Для тренировки можете разложить на простые множители следующие числа: 256, 378, 512.
Нахождение делителей числа
В начале данного урока было сказано, что делителем называется число, на которое другое число делится без остатка.
Например, число 2 является делителем числа 6, поскольку число 6 можно без остатка разделить на 2
6 : 2 = 3
Ещё делителем числа 6 является число 3
6 : 3 = 2
Ещё делителем числа 6 является число 1
6 : 1 = 6
Наконец, делителем числа 6 является само это число
6 : 6 = 1
Перечислим все делители числа 6
1, 2, 3, 6
Иногда возникает необходимость найти все делители какого-нибудь числа. Чтобы понять, как это делается, рассмотрим несколько примеров.
Пример 1. Найти делители числа 12
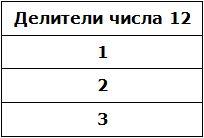
Во-первых, единица является делителем любого числа. Пусть и у нас первым делителем числа 12 будет 1
Теперь раскладываем число 12 на простые множители:
Получили разложение 2 × 2 × 3.
В процессе разложения числа 12 на простые множители, мы делили его на числа 2 и 3. На них число 12 разделилось без остатка, значит они тоже являются делителями числа 12. Внесём эти два числа в нашу таблицу делителей:
Чтобы получить остальные делители числа 12, нужно найти все возможные произведения его простых множителей между собой. Получаемые в результате ответы и будут остальными делителями числа 12.
Число 12 мы разложили на простые множители 2 × 2 × 3. Найдём все возможные произведения этих простых множителей между собой. Первое произведение это 2 × 2. Это произведение равно 4
Занесём число 4 в нашу таблицу делителей
Следующее возможное произведение из простых множителей числа 12 это произведение 2 × 3. Данное произведение равно 6. Занесём число 6 в нашу таблицу делителей:
Последнее возможное произведение из простых множителей числа 12 это произведение из всех его множителей, а именно 2 × 2 × 3. Это произведение равно 12. Занесём число 12 в нашу таблицу делителей:
Таким образом, делителями числа 12 являются числа 1, 2, 3, 4, 6, 12.
На основании приведённого примера можно сформировать правило для нахождения делителей числа:
Чтобы найти делители числа, нужно:
Пример 2. Найти делители числа 6
Первым делителем числа 6 запишем единицу:
Теперь разложим число 6 на простые множители:
Выпишем из полученного разложения те множители, которые являются делителями числа 6. Видим, что это множители 2 и 3. Они будут следующими делителями числа 6. Допишем их к нашим делителям:
1, 2, 3
1, 2, 3, 6