Как упростить выражение информатика
Как упростить выражение информатика
Логические операции (конъюнкция, дизъюнкция, инверсия)
Таблица истинности: К онъюнкция (логическое умножение, логическое И) обозначается /\
(например, А /\ В) либо & (например, А & В); в языках программирования обозначение «And».
Таблица истинности: Дизъюнкция (логическое сложение, логическое ИЛИ) обозначается \/ (например, А \/ В);
в языках программирования обозначение «Or».
Инверсией двух высказываний называется новое высказывание, которое истинное тогда и только тогда, когда исходное высказывание ложно.
Название логической операции
Конъюнкция, логическое умножение
Дизъюнкция, логическое сложение
тогда и только тогда, когда
эквивалентность, эквиваленция, равнозначность
Соединим оба утверждения в одно высказывание:
Составим таблицу истинности на полученное высказывание:
Учитывая то, что предположения двух друзей подтвердились, а предположения третьего неверны, запишем и упростим истинное высказывание
Высказывание 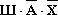
Пусть дана таблица истинности для некоторой логической функции Z(X,Y):
Построим истинностную таблицу сложного высказывания :
Очевидно, истинностная таблица будет содержать 


Информатика. 10 класс
Конспект урока
Информатика, 10 класс. Урок № 12.
Тема — Преобразование логических выражений
Перечень вопросов, рассматриваемых в теме: основные законы алгебры логики, преобразование логических выражений, логические функции, построение логического выражения с данной таблицей истинности и его упрощение, дизъюнктивная и конъюнктивная нормальная форма, совершенная дизъюнктивная нормальная форма (СДНФ), совершенная конъюнктивная нормальная форма (СКНФ).
Глоссарий по теме: основные законы алгебры логики, логические функции, дизъюнктивная и конъюнктивная нормальная форма, совершенная дизъюнктивная нормальная форма (СДНФ), совершенная конъюнктивная нормальная форма (СКНФ)
Основная литература по теме урока:
Л. Л. Босова, А. Ю. Босова. Информатика. Базовый уровень: учебник для 10 класса
— М.: БИНОМ. Лаборатория знаний, 2017 (с.197—209)
Открытые электронные ресурсы по теме:
Теоретический материал для самостоятельного изучения.
Способ определения истинности логического выражения путем построения его таблицы истинности становится неудобным при увеличении количества логических переменных, т.к. за счет существенного увеличения числа строк таблицы становятся громоздкими. В таких случаях выполняются преобразования логических выражений в равносильные. Для этого используют свойства логических операций, которые иначе называют законами алгебры логики.
Основные законы алгебры логики
Справедливость законов можно доказать построением таблиц истинности.
Пример 1. Упростим логическое выражение
Последовательно применим дистрибутивный закон и закон исключенного третьего:
В общем случае можно предложить следующую последовательность действий:
Пример 2. Упростим логическое выражение 
Здесь последовательно использованы замена операции импликация, закон де Моргана, распределительный закон, закон противоречия и операция с константой, закон идемпотентности и поглощения.
Аналогичные законы выполняются для операции объединения, пересечения и дополнения множеств. Например:
Пример 3. На числовой прямой даны отрезки B = [2;12] и C = [7;18]. Каким должен быть отрезок A, чтобы предикат 
Преобразуем исходное выражение, избавившись от импликации:
A, B, C — множества. Для них можно записать 
Будем считать, что
Тогда 
Так как множество B — это отрезок [2;12], а множество 



Пример 4. Для какого наименьшего неотрицательного целого десятичного числа а выражение

Перепишем исходное выражение в наших обозначениях и преобразуем его:
Рассмотрим предикат 

Рассмотрим предикат 

Рассмотрим предикат 
По условию задачи надо, чтобы 
Запишем это выражение для рассмотренных множеств истинности:
Так как 

Объединением множеств M и N являются все двоичные числа, у которых хотя бы один из битов с номерами 5, 4, 3, 2, 0 содержит единицу. Пересечением этого множества с множеством K будут все двоичные числа, у которых биты с номерами 4 и 0 будут заняты нулями, т.е. такие двоичные числа, у которых хотя бы один из битов с номерами 5, 3, 2 содержит 1. Все эти числа образуют множество А.
Искомое число a должно быть таким, чтобы при любом неотрицательном целом значении переменной х: 
Значение любого логического выражения определяется значениями входящих в него логических переменных. Тем самым логическое выражение может рассматриваться как способ задания логической функции.
Для n=2 существует 16 различных логических функций. Рассмотрим их подробнее.
Как упростить выражение информатика
При упрощении сложных высказываний рекомендуется использовать основные законы преобразования логики и свойства констант.
Пример 1.
(вынесем А за скобки и далее по закону исключения третьего)
1 способ:
Применим закон дистрибутивности:
2 способ:
Перемножим скобки (как в алгебре чисел) и далее на основании закона дистрибутивности.
1 способ:
представим Х как Х *1, а 1 распишем как У + не У.
законы идемпотентности позволяют добавлять в выражение любое из уже имеющихся в нем слагаемых, добавим к полученному выражению Х&У
2 способ:
Так как умножение выполняется первым, то можно поставить скобки, а далее по закону дистрибутивности:
Х + не Х * У = Х + (не Х * У) = (Х + не Х) * (Х + У) = 1 * (Х + У) = Х + У
2 способ:
Применим закон де Моргана
Попробуйте упростить высказывания:
Как упростить выражение информатика
Изучить основы алгебры логики.
Задачи лабораторной работы
В результате прохождения занятия студент должен:
Общие теоретические сведения
Основные понятия алгебры логики
Логической основой компьютера является алгебра логики, которая рассматривает логические операции над высказываниями.
Алгебра логики – это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.
Логическое высказывание – это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.
Не всякое предложение является логическим высказыванием.
Пример. предложение «Давайте пойдем в кино» не является высказыванием. Вопросительные и побудительные предложения высказываниями не являются.
Высказывательная форма – это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями.
Высказывания, образованные из других высказываний с помощью логических связок, называются составными (сложными). Высказывания, которые не являются составными, называются элементарными (простыми).
Чтобы обращаться к логическим высказываниям, им назначают имена.
Пример. Обозначим через А простое высказывание «число 6 делится на 2», а через В простое высказывание «число 6 делится на 3». Тогда составное высказывание «Число 6 делится на 2, и число 6 делится на 3» можно записать как «А и В». Здесь «и» – логическая связка, А, В – логические переменные, которые могут принимать только два значения – «истина» или «ложь», обозначаемые, соответственно, «1» и «0».
| Обозначение операции | Читается | Название операции | Альтернативные обозначения | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ¬ | НЕ | Отрицание (инверсия) | Черта сверху | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ИЛИ | Дизъюнкция (логическое сложение) | + | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| → | Если … то | Импликация | Пример. Пусть А=«Сегодня пасмурно», тогда ¬А=«Сегодня не пасмурно». И Операция, выражаемая связкой «и», называется конъюнкцией (лат. conjunctio – соединение) или логическим умножением и обозначается точкой « • » (может также обозначаться знаками (или плюсом). Высказывание А . Высказывание А↔В истинно тогда и только тогда, когда значения А и В совпадают. ЛИБО … ЛИБО Операция, выражаемая связками «Либо … либо», называется исключающее ИЛИ или сложением по модулю 2 и обозначается XOR или Пример. Высказывание «Число 6 либо нечетно либо делится без остатка на 2» является истинным, а высказывание «Либо число 6 четно либо число 6 делится на 3» – ложно, так как истинны оба высказывания входящие в него.
Порядок выполнения логических операций задается круглыми скобками. Но для уменьшения числа скобок договорились считать, что сначала выполняется операция отрицания («не»), затем конъюнкция («и»), после конъюнкции – дизъюнкция («или») и исключающего или и в последнюю очередь – импликация и эквиваленция. С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением). Пример.
Опираясь на данные таблицы истинности основных логических операций можно составлять таблицы истинности для более сложных формул. 3. Заполнить столбцы с учетом таблиц истинности логических операций (табл. 3).
3. Заполнить столбцы с учетом таблиц истинности логических операций (табл. 5).
Поскольку любая логическая операция может быть представлена в виде комбинации трех основных, любые устройства компьютера, производящие обработку или хранение информации, могут быть собраны из базовых логических элементов, как из “кирпичиков”. Логические элементы компьютера оперируют с сигналами, представляющими собой электрические импульсы. Есть импульс – логический смысл сигнала – 1, нет импульса – 0. На входы логического элемента поступают сигналы-значения аргументов, на выходе появляется сигнал-значение функции. Алгоритм построения логических схем.Логические законы и правила преобразования логических выражений
|
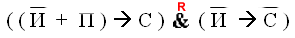
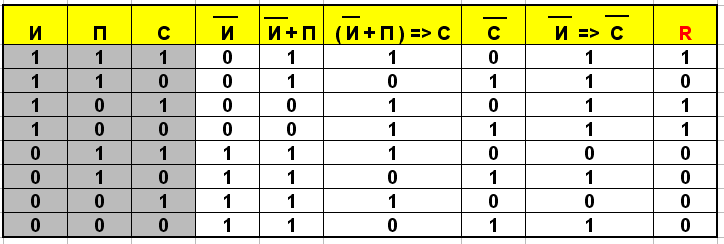
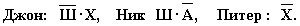
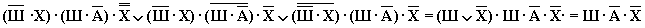


















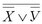





 .
. – логическая функция двух переменных A и B.
– логическая функция двух переменных A и B.











