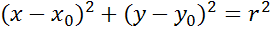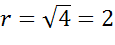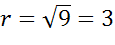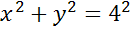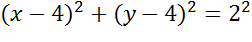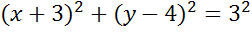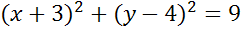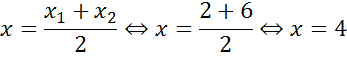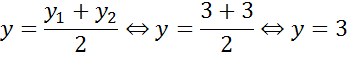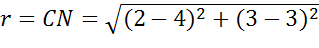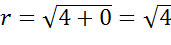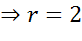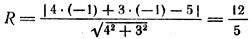уравнение окружности что такое

Уравнение окружности.

Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.

В формулировке окружности упоминается расстояние между точкой окружности и центром.

Формула расстояния между двумя точками М₁(х₁; у₁) и М₂(х₂; у₂) имеет вид:

,

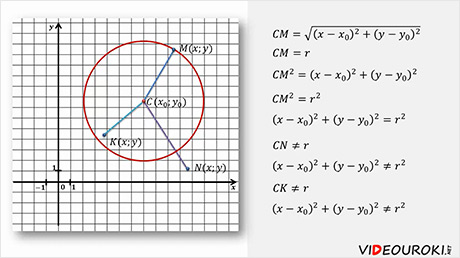
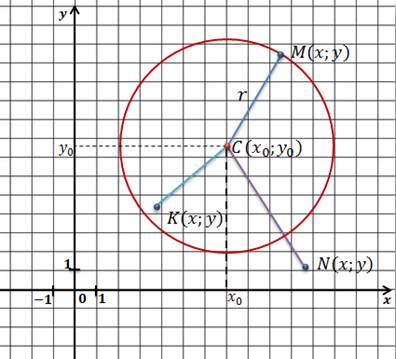
Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х₀; у₀) и радиусом r.

Отметим произвольную точку М(х; у) на этой окружности.

.

Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.

Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х₀ ) 2 +(у – у₀ ) 2 = r 2 .

Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х₀; у₀) и радиусом r имеет вид:

В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):

Источник

Уравнение окружности

Урок 16. Геометрия 9 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Уравнение окружности»

Прежде всего, давайте вспомним, формулу расстояния между двумя точками и еще, повторим, что уравнение с двумя переменными x и y называется уравнением линии l, если этому уравнению удовлетворяют координаты любой точки линии l и не удовлетворяют координаты никакой точки, не лежащей на этой линии.

Сегодня на уроке мы попробуем по геометрическим свойствам линии найти ее уравнение.

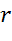
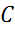
В качестве линии рассмотрим окружность радиуса с центром в точке .

Задача. Записать уравнение окружности с радиусом 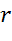и центром в начале координат.

Начало координат имеет координаты (0;0). Подставим их в уравнение окружности и получим, что уравнение окружности с радиусом r и центром в начале координат имеет вид

.

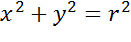
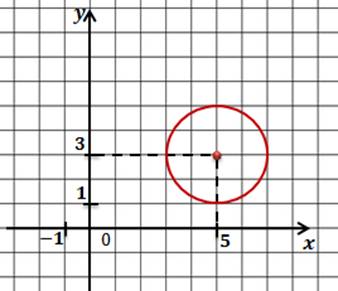
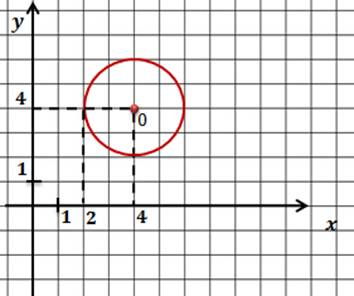
Задача. Начертить окружность, заданную уравнением .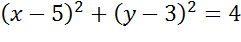

Запишем общее уравнение окружности и проанализируем исходное уравнение. Прежде всего, определимся с координатами центра окружности. Это будут числа 5 и 3. Теперь давайте определим величину радиуса окружности.

Поскольку в правой части формулы стоит квадрат радиуса, то для того, чтобы найти радиус надо извлечь квадратный корень из 4. Получим 2.

Значит наша формула задает окружность с центром в точке с координатами пять три и радиусом равным двум.

Задача. Начертить окружность, заданную уравнением .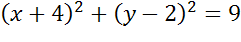

Запишем общее уравнение окружности и проанализируем исходное уравнение. Прежде всего определимся с координатами центра окружности.

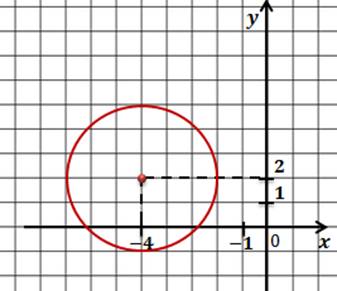
Задача. Начертить окружность, заданную уравнением .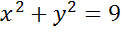

Решение. Уравнениями такого типа описываются окружности с центром в начале координат. Теперь давайте определим величину радиуса окружности. Поскольку в правой части формулы стоит квадрат радиуса, то для того, чтобы найти радиус надо извлечь квадратный корень из 9.

Значит наша формула задает окружность с центром в точке с координатами (0;0) и радиусом равным 3.

Теперь давайте попробуем решить задачу обратную данным.

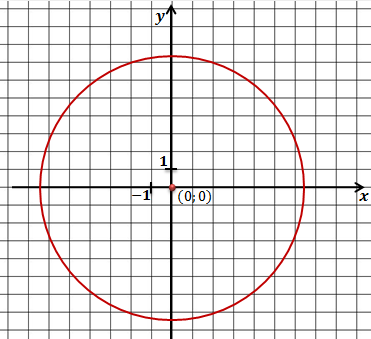
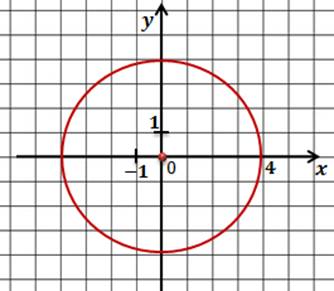
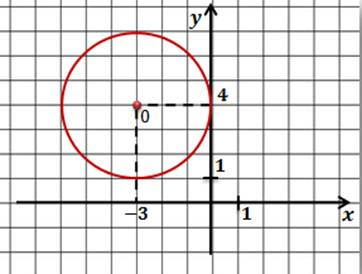
Задача. Составить уравнение окружности, которая показана на рисунке.

Как и в предыдущих задачах мы начнем с определения координат центра окружности. Сделать это нетрудно. Центр этой окружности совпадает с началом координат, поэтому центр окружности имеет координаты (0;0).

Нетрудно заметить, что радиус окружности равен 4.

Запишем уравнение окружности и подставим найденные значения.

Ответ: .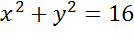

Решим еще одну задачу.

Задача. Составить уравнение окружности, которая показана на рисунке.

– центр окружности

– радиус окружности

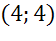
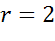
Ответ:.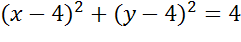

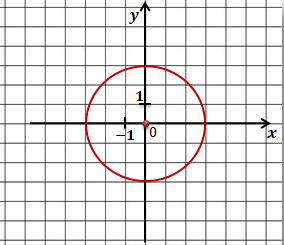
Задача. Составить уравнение окружности, которая показана на рисунке.

– центр окружности

– радиус окружности

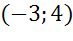
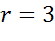
Ответ:.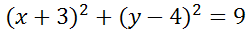

Решая задачи, мы с вами выполняли один и тоже порядок действий. Давайте еще раз повторим этот порядок.

Для того, что бы составить уравнение окружности и построить ее надо:

1. Найти координаты центра окружности.

2. Найти длину радиуса этой окружности.

3. Записать уравнение окружности.

4. Подставить полученные значения в уравнение окружности.

5. Построить окружность, если это требуется для решения задачи.

Рассмотрим еще одну задачу.

Написать уравнение окружности с диаметром эм эн, если точка эн имеет координаты два три, точка эм имеет координаты шесть три.

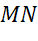
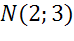
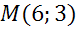
Задача. Написать уравнение окружности с диаметром , если , .

Найдем координаты центра окружности. Центр окружности является серединой диаметра. Воспользуемся формулами для нахождения координат середины отрезка.

Получим, что центр окружности имеет координаты .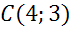

Теперь определим радиус окружности. Для этого найдем расстояние от центра окружности до концов диаметра.

Запишем общее уравнение окружности и подставим в него найденные значения. Тогда получим, что уравнение данной окружности имеет вид:

Ответ: .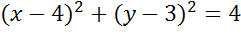

Подведем итоги урока.

На сегодняшнем уроке мы познакомились с формулой, которая задает окружность с центром в точке С (x₀; y₀) и радиусом r.

Также мы познакомились с формулой, которая задает окружность с центром в начале координат и радиусом r.

Мы рассмотрели задачи на составление уравнения окружности по рисунку и на построение окружности по заданному уравнению.

Источник

Геометрия. Урок 5. Окружность

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Определение окружности

Окружность – геометрическое место точек, равноудаленных от данной точки.

Отрезки в окружности

Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.

Хорда a – отрезок, соединяющий две точки на окружности.

Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).

O A – радиус, D E – хорда, B C – диаметр.

Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.

Касательная к окружности – прямая, имеющая с окружностью одну общую точку.

Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.

Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).

Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.

Дуга в окружности

Теорема 4:
Равные хорды стягивают равные дуги.

Углы в окружности

В окружности существует два типа углов: центральные и вписанные.

Центральный угол – угол, вершина которого лежит в центре окружности.

∠ A O B – центральный.

Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.

Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.

∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2

∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °

Длина окружности, длина дуги

Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.

Длина окружности находится по формуле:

Площадь круга и его частей

Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.

Круг – часть пространства, которая находится внутри окружности.

Иными словами, окружность – это граница, а круг – это то, что внутри.

Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.

Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.

Площадь круга находится по формуле: S = π R 2

Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Примеры сектора в реальной жизни: кусок пиццы, веер.

Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α

Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.

Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.

Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.

S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α

Теорема синусов

Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:

a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с окружностями.

Источник

Уравнение окружности

Окружностью называется множество точек плоскости, равноудаленных от данной точки, называемой центром.

Если точка С — центр окружности, R — ее радиус, а М — произвольная точка окружности, то по определению окружности

Равенство (1) есть уравнение окружности радиуса R с центром в точке С.

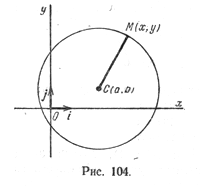
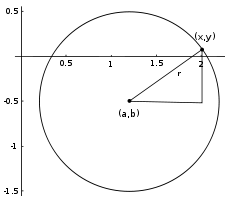
Пусть на плоскости задана прямоугольная декартова система координат (рис. 104) и точка С(а; b) — центр окружности радиуса R. Пусть М(х; у) — произвольная точка этой окружности.

Так как |СМ| = \( \sqrt <(x — a)^2 + (у — b)^2>\), то уравнение (1) можно записать так:

(x — a) 2 + (у — b) 2 = R 2 (2)

Уравнение (2) называют общим уравнением окружности или уравнением окружности радиуса R с центром в точке (а; b). Например, уравнение

есть уравнение окружности радиуса R = 5 с центром в точке (1; —3).

Если центр окружности совпадает с началом координат, то уравнение (2) принимает вид

Уравнение (3) называют каноническим уравнением окружности.

Задача 1. Написать уравнение окружности радиуса R = 7 с центром в начале координат.

Непосредственной подстановкой значения радиуса в уравнение (3) получим

Задача 2. Написать уравнение окружности радиуса R = 9 с центром в точке С(3; —6).

Подставив значение координат точки С и значение радиуса в формулу (2), получим

(х — 3) 2 + (у — (—6)) 2 = 81 или (х — 3) 2 + (у + 6) 2 = 81.

Задача 3. Найти центр и радиус окружности

Сравнивая данное уравнение с общим уравнением окружности (2), видим, что а = —3, b = 5, R = 10. Следовательно, С(—3; 5), R = 10.

Задача 4. Доказать, что уравнение

является уравнением окружности. Найти ее центр и радиус.

Преобразуем левую часть данного уравнения:

Это уравнение представляет собой уравнение окружности с центром в точке (—2; 1); радиус окружности равен 3.

Задача 5. Написать уравнение окружности с центром в точке С(—1; —1), касающейся прямой АВ, если A (2; —1), B(— 1; 3).

Напишем уравнение прямой АВ:

или 4х + 3y —5 = 0.

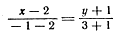
Так как окружность касается данной прямой, то радиус, проведенный в точку касания, перпендикулярен этой прямой. Для отыскания радиуса необходимо найти расстояние от точки С(—1; —1) — центра окружности до прямой 4х + 3y —5 = 0:

Напишем уравнение искомой окружности

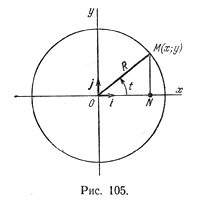
Пусть радиус-вектор OM > точки М образует угол величины t с положительным направлением оси Ох, тогда абсцисса и ордината точки М изменяются в зависимости от t

(0 2 = 3 cos 2 t, у 2 = 3 sin 2 t. Складывая эти равенства почленно, получаем

Источник

Окружность

Окружность — геометрическое место всех точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное неотрицательное расстояние, называемое её радиусом.

Содержание

Другие определения

Окружность диаметра AB — это фигура, состоящая из точек A, B и всех точек плоскости, из которых отрезок AB виден под прямым углом.

Окружность — это фигура, состоящая из всех точек плоскости, для каждой из которых отношение расстояний до двух данных точек равно данному числу, отличному от единицы. (см. Окружность Аполлония)

Также фигура, состоящая из всех таких точек, для каждой из которых сумма квадратов расстояний до двух данных точек равна заданной величине, большей половины квадрата расстояния между данными точками.

Связанные определения

Свойства

Основные формулы

Площадь круга радиуса R:

Площадь сектора, ограниченного углом α, измеряемым в градусах, радиусом R:

Площадь сегмента, ограниченного дугой окружности углом α, хордой:

Уравнения

Декартовы координаты

Общее уравнение окружности записывается как:

Точка — центр окружности, — её радиус.

Уравнение окружности радиуса с центром в начале координат:

Уравнение окружности, проходящей через три точки (с помощью определителя) и

Окружность также можно описать с помощью параметрического уравнения:

В декартовой системе координат окружность не является графиком функции, но она может быть описана как объединение графиков двух следующих функций:

Если центр окружности совпадает с началом координат, функции принимают вид:

Полярные координаты

Окружность радиуса с центром в точке :

Если полярные координаты центра окружности то проходящая через начало координат окружность описывается уравнением:

Если же центр является началом координат, то уравнение будет иметь вид:

Комплексная плоскость

На комплексной плоскости окружность задаётся формулой:

или в параметрическом виде

Касательные и нормали

Уравнение касательной к окружности в точке определяется уравнением

Уравнение нормали в той же точке можно записать как

Концентрические и ортогональные окружности

Две окружности, заданные уравнениями:

являются концентрическими (то есть имеющими общий центр) в том и только в том случае, когда и

Две окружности являются ортогональными (то есть пересекающиеся под прямым углом) тогда и только тогда, когда выполняется условие

См. также

Литература

Циклоида • Эпициклоида • Гипоциклоида • Трохоида (Удлинённая + Укороченная циклоида) • Эпитрохоида (Удлинённая + Укороченная эпициклоида • («Роза») • Гипотрохоида • Скорейшего спуска (Брахистохрона, дуга циклоиды)

Конические сечения
Главные типы	Эллипс • Гипербола • Парабола
Вырожденные	Точка • Прямая • Пара прямых
Частный случай эллипса	Окружность
Геометрическое построение	Коническое сечение • Шары Данделена
См. также	Коническая константа
Математика • Геометрия

Полезное

Смотреть что такое «Окружность» в других словарях:

окружность — кольцо, эпицикл, кривая, местность, околоток, окрестность, деферент, круг, округа Словарь русских синонимов. окружность 1. см. круг. 2. см. окрестность … Словарь синонимов

ОКРУЖНОСТЬ — ОКРУЖНОСТЬ, замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра). Отрезок R, соединяющий центр окружности с какой либо её точкой (а также длина этого отрезка), называется радиусом; отрезок, соединяющий две точки… … Современная энциклопедия

ОКРУЖНОСТЬ — замкнутая плоская кривая, все точки которой одинаково удалены от ее центра O. (рис.). Расстояние R каждой точки окружности до ее центра называется радиусом. Прямая АВ, соединяющая любые две точки окружности, называется ее хордой, хорда CD,… … Большой Энциклопедический словарь

ОКРУЖНОСТЬ — ОКРУЖНОСТЬ, расстояние, измеряемое по краю плоской геометрической фигуры, именуемой кругом, для которого это расстояние определяется как 2pr, где r радиус. Изредка этот термин применяют также к другим фигурам … Научно-технический энциклопедический словарь

ОКРУЖНОСТЬ — ОКРУЖНОСТЬ, окружности, жен. 1. Замкнутая кривая, все точки которой равно удалены от точки, называемой центром; замкнутая кривая, ограничивающая плоскость круга (мат.). 2. Линия измерения кругообразных поверхностей и предметов. Яма метров десяти… … Толковый словарь Ушакова

ОКРУЖНОСТЬ — ОКРУЖНОСТЬ, и, жен. 1. В математике: замкнутая на плоскости кривая, все точки к рой равно удалены от центра. 2. Линия измерения округлых, кругообразных поверхностей и предметов. О. водоёма. Воронка пяти метров в окружности. 3. Окружающая… … Толковый словарь Ожегова

Окружность — кривая линия, все точки которой находятся на одинаковомрасстоянии от одной внутренней точки, называемой центром. Прямые,проведенный из центра к точкам О., называются paдиуcaми. Прямая,проходящая чрез две точки О. и ограниченная этими точками,… … Энциклопедия Брокгауза и Ефрона

окружность — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN round … Справочник технического переводчика

ОКРУЖНОСТЬ — замкнутая плоская кривая, все точки которой находятся на одинаковом расстоянии от некоторой точки О, лежащей в плоскости этой кривой и называемой её центром. Расстояние от любой точки окружности до её центра измеряется отрезком, называемым… … Большая политехническая энциклопедия

окружность — и; ж. 1. Матем. Замкнутая на плоскости кривая, все точки которой равно удалены от центра. 2. Линия измерения округлых, кругообразных поверхностей и предметов. О. озера. Воронка трёх метров в окружности. 3. Устар. Окружающая местность, округа. ◁ В … Энциклопедический словарь

Источник