тетраэдр это что такое фото
Значение слова «тетраэдр»
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
ТЕТРА’ЭДР [тэ], а, м. [от греч. tetra- — четырех- и hedra — основание] (мат.). Четырехгранник, каждая грань к-рого представляет собой треугольник, напр. пирамида.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
тетра́эдр
1. геометр. многогранник с четырьмя треугольными гранями ◆ Рассмотрим двумерный симплициальный комплекс, состоящий из четырех граней тетраэдра. М. Кац, С. Улам, «Математика и логика», 1971 г.
Фразеологизмы и устойчивые сочетания
Делаем Карту слов лучше вместе

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова белозерец (существительное):
Ассоциации к слову «тетраэдр»
Синонимы к слову «тетраэдр»
Предложения со словом «тетраэдр»
Сочетаемость слова «тетраэдр»
Каким бывает «тетраэдр»
Понятия со словом «тетраэдр»
Отправить комментарий
Дополнительно
Предложения со словом «тетраэдр»
Кристаллическая чёрная гора в форме тетраэдра обладала колоссальной массой, притягивая к себе все предметы.
Квадраты, формирующие кубический атом земли, могут быть составлены из двух равнобедренных прямоугольных треугольников, а треугольные грани тетраэдра, октаэдра и икосаэдра, представляющих атомы огня, воздуха и воды (в указанном порядке), могут быть составлены из двух других прямоугольных треугольников.
Чтобы разобраться с этим вопросом, заметим, что вершины тетраэдра, октаэдра и икосаэдра объединяют три, четыре и пять треугольников, сходящихся вместе, и зададим вопрос: «Что произойдёт, если мы продолжим и их будет шесть?» Тогда мы поймём, что шесть равносторонних треугольников, имеющих общую вершину, будут лежать на плоскости.
Ортоцентрический тетраэдр
Тетраэдр, все высоты которого, опущенные из вершин на противоположные грани, пересекаются в одной точке, называется ортоцентрическим.
Другие определения ортоцентрического тетраэдра, равносильные друг другу
Использованные материалы
Полезное
Смотреть что такое «Ортоцентрический тетраэдр» в других словарях:
Тетраэдр — (греч. τετραεδρον четырёхгранник) простейший многогранник, гранями которого являются четыре треугольника. У тетраэдра 4 грани, 4 вершины и 6 рёбер. Содержание 1 Связанные определения … Википедия
Правильный тетраэдр — Тетраэдр Тип Правильный многогранник Грань Правильный треугольник Вершин … Википедия
Равногранный тетраэдр — Тетраэдр называется равногранным, если все его грани равные между собой треугольники. Существует ряд эквивалентных определений: описанный около него параллелепипед прямоугольный; его развёртка, полученная при разрезании его по трём… … Википедия
Правильный многогранник — Додекаэдр Правильный многогранник или платоново тело это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией … Википедия
Звёздчатый многогранник — Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей. Звёздчатый многогранник (звёздч … Википедия
Правильные многомерные многогранники — Правильный n мерный многогранник многогранники n мерного евклидова пространства, которые являются наиболее симметричными в некотором смысле. Правильные трёхмерные многогранники называются также платоновыми телами. Содержание 1 Определение 2 … Википедия
Куб — У этого термина существуют и другие значения, см. Куб (значения). Куб Тип Правильный многогранник Грань квадрат … Википедия
Двойственный многогранник — Многогранник, двойственный (или дуальный) к заданному многограннику многогранник, у которого каждой грани исходного многогранника соответствует вершина двойственного, каждой вершине исходного грань двойственного и каждому ребру… … Википедия
Икосаэдр — анимация Тип Правильный многогранник Грань Правильный треугольник Граней 20 … Википедия
Полуправильный многогранник — Полуправильные многогранники в общем случае это различные выпуклые многогранники, имеющие определённые признаки правильных, такие как одинаковость всех граней или являемость всех граней правильными многоугольниками, а также пространственная … Википедия
Правильный тетраэдр
| Тетраэдр | |
|---|---|
 | |
| Тип | Правильный многогранник |
| Грань | Правильный треугольник |
| Вершин |  |
| Рёбер |  |
| Граней |  |
| Граней при вершине |  |
| Длина ребра |  |
| Площадь поверхности |  |
| Объём |  |
| Высота |  |
| Радиус вписаной сферы |  |
| Радиус описанной сферы |  |
| Угол наклона ребра |  |
| Угол наклона грани |  |
| Группа симметрий | Тетраэдральная (Th) |
| Двойственный многогранник | Тетраэдр |
Тетраэдр называется правильным, если все его грани — равносторонние треугольники.
У правильного тетраэдра все двугранные углы при рёбрах и все трёхгранные углы при вершинах равны.



 Многогранники
Многогранники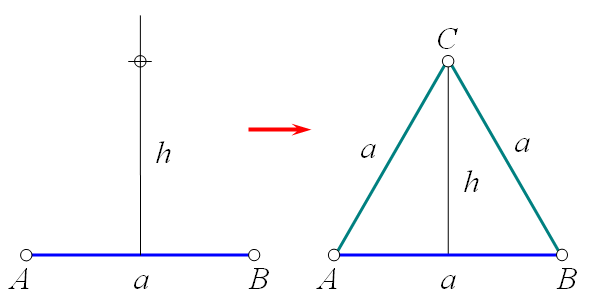
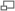

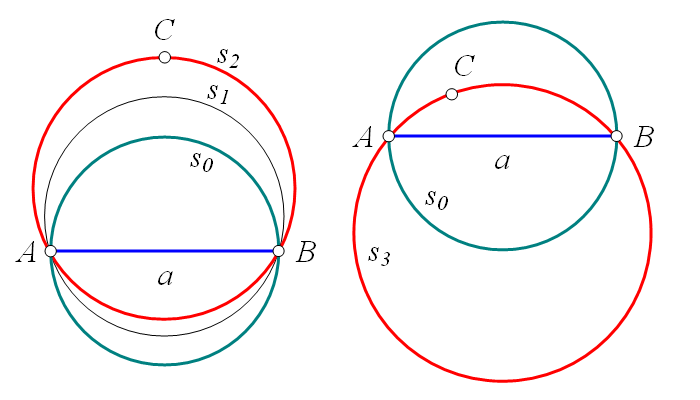







 – число сочетаний из n по m.
– число сочетаний из n по m.







