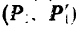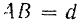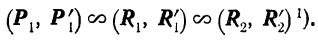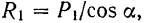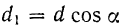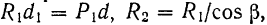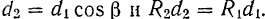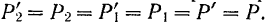теорема об эквивалентных парах сил формулируется так

Инструменты пользователя

Инструменты сайта

Боковая панель

Теория вероятностей и математическая статистика
Строительная механика для строительных специальностей
Матанализ. Дифференциальное и интегральное исчисление
economics

Теоретическая механика. Статика:

Контакты

Теоремы об эквивалентности пар

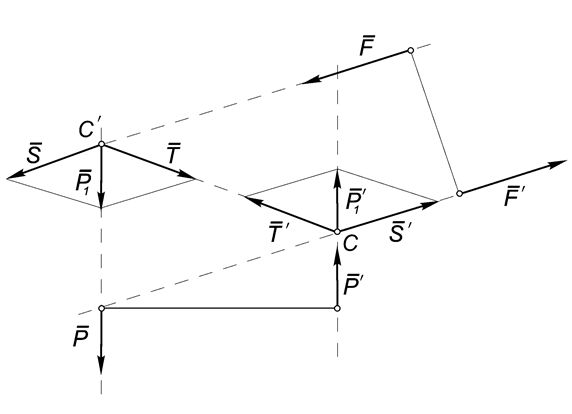
Теорема 1. ( Об эквивалентности пар на плоскости ). Две пары, лежащие в одной плоскости и имеющие равные по величине и по знаку моменты, эквивалентны.

Продолжим линии действия сил пар до их пересечения в точках С и С’.

В силу теоремы Вариньона:

Рассмотрим следствия этой теоремы, которые также можно рассматривать как свойства пар сил в дополнение к свойствам, рассмотренным в «Пара сил и ее свойства».

Следствия:

Таким образом, термин «момент» имеет в ТМ два значения:

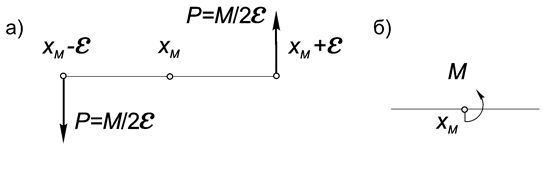
Отметим, что при таком предельном переходе плечо пары стремится к нулю, а силы пары – к бесконечности. Полученный в соответствии с определением 1 момент фактически является таким же самостоятельным объектом в механике, как и сила, и в дальнейшем мы будем обозначать его так, как показано на рис.2б.

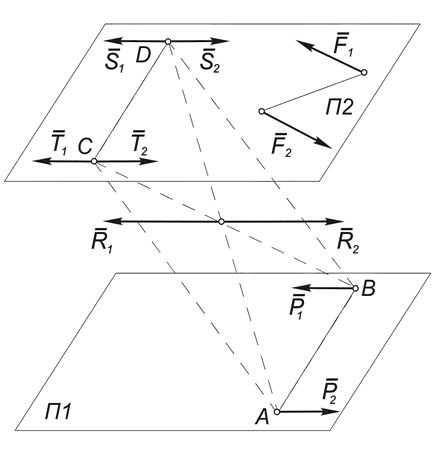
Теорема 2. ( Об эквивалентности пар в пространстве ). Две пары, лежащие в параллельных плоскостях и имеющие равные по величине и по знаку моменты, эквивалентны.

Для доказательства этой теоремы нам понадобится следующая:

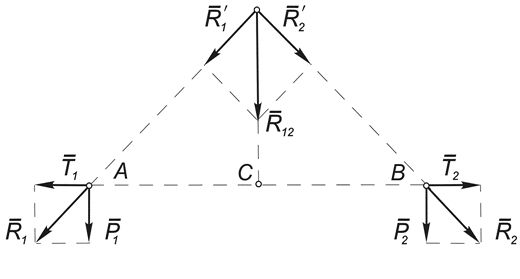
Лемма. Равнодействующая двух параллельных и равных по модулю сил равна их сумме, а ее линия действия проходит посредине между точками их приложения ( Рис.3 ).

На основании аксиом 2, 3 и последней леммы:

Следствие. Действие пары сил на ТТ не изменится при ее перемещении в параллельную плоскость, расположенную в пределах этого тела.

Источник

Основные свойства пары

Основные свойства пары характеризуются следующими тремя теоремами.

Теорема I. Пара сил не имеет равнодействующей.

Это значит, что при F₁=F₂ равнодействующая не существует.

Из этой теоремы следует, что пара сил не может быть уравновешена одной силой; пара сил может быть уравновешена только парой.

Теорема II. Алгебраическая сумма моментов сил, составля­ющих пару, относительно любой точки плоскости действия пары есть величина постоянная, равная моменту пары.

Из этой теоремы следует, что при любом центре моментов пара сил войдет в уравнение моментов с одним и тем же знаком и одной и той же величиной.

Теорема III. Алгебраическая сумма проекций сил пары на ось всегда равна нулю.

Из этой теоремы следует, что пара сил не входит ни в уравнение сил, ни в уравнение проекций сил.

Теорема о сложении пар

Теорема. Всякая плоская система пар эквивалента одной результирующей паре, момент которой равен алгебраической сумме моментов данных пар.

Эквивалентные пары

Две пары называются эквивалентными, если одну из них можно заменить другой, не нарушая механического состояния свободного твердого тела.

Теорема об эквивалентных парах формулируется так: если моменты двух пар алгебраически равны, то эти пары эквивалентны.

Из доказанной теоремы об эквивалентных парах вытекает четыре следствия:

1. не изменяя механического состояния тела, пару можно
перемещать как угодно в плоскости ее действия;

2. не изменяя механического состояния тела, можно менять
силы и плечо пары, но так, чтобы ее момент остаются неизменным;

3. чтобы задать пару, достаточно задать ее момент, поэтому иногда слово «пара» заменяют словом «момент» и условно изображают его так, как показано на рис. 4.6;

4. условия равновесия плоской системы па­раллельных сил будут справедливы, если вместе с такой системой действуют и пары сил, так как их можно повернуть в плоскости действия и поставить силы пары параллельно другим силам системы.

Условие равновесия плоской системы пар

Применяя доказанную в предыдущем параграфе теорему к плоской системе пар, находящейся в равновесии, запишем

Поэтому условие равновесия плоской системы пар в общем виде будет выглядеть так:

а формулируется следующим образом: для равновесия плоской системы пар необходимо и достаточно, чтобы алгебраическая сумма моментов данных пар равнялась нулю/

Различные случаи приведения плоской системы произвольно расположенных сил

Изучив свойства главного вектора и главного момента, укажем четыре возможных случая приведения плоской системы произвольно расположенных сил:

1. F_гл≠0, М_гл≠0, т. е. главный вектор и главный момент
не равны нулю. В этом случае система сил эквивалентна
равнодействующей, которая равна по модулю главному век­
тору, параллельна ему, направлена в ту же сторону, но по
другой линии действия (см. § 5.3, п. 3).

2. F_гл≠0, М_гл=0. В этом случае система сил эквивалентна
равнодействующей, линия действия которой проходит через
центр приведения и совпадает с главным вектором.

3. F_гл=0, М_гл≠0. В этом случае система эквивалентна
паре. Так как модуль и направление главного вектора во
всех случаях не зависят от выбора центра приведения, то
в рассматриваемом случае величина и знак главного момента
тоже не зависят от центра приведения, ибо одна и та же
система сил не может быть эквивалентна различным парам.

4. F_гл=0, М_гл=0. В этом случае система сил эквивалентна
нулю, т. е. находится в равновесии.

Источник

1. Не изменяя действия пары сил на твердое тело, ее можно перемещать в плоскости действия, поворачивать, менять модули сил, составляющих пару, и ее плечо, так чтобы момент пары не изменялся

Таким образом момент пары сил равен моменту исходной пары сил. В тоже время модули сил, составляющих эти пары разные, так же как и плечи этих пар.

2. Не изменяя действия пары сил на твердое тело, ее можно пере-

мещать в другую плоскость, параллельную исходной плоскости дей-

момент которой равен сумме вектор моментов исходных пар.

9. Систему сил, приложенных к телу, можно упростить, используя теорему о параллельном переносе силы. В результате приведения произвольной пространственной системы сил к данному центру в общем случае получаем главный вектор, равный геометрической сумме всех сил системы, и главный момент, равный геометрической сумме моментов всех приводимых сил относительно центра приведения (рис. 1.33). Сложим и т.д., получим силовой многоугольник, где

Затем векторно сложим векторы моментов

Главный вектор инвариантен по отношению к центру приведения. Главный момент зависит от вы-бора центра приведения. По модулю главный вектор вычисляется

Где

Направление находим по направляющим косинусам

Главный момент

Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех этих сил на каждую из координатных осей равнялась нулю, и чтобы алгебраическая сумма моментов всех сил системы относительно каждой из трех координатных осей равнялась нулю.

Система параллельных сил. Если ось OZ параллельна силам, то три уравнения (1.23) обращаются в тождества, так как проекции сил на оси OX и OY и их моменты относительно оси OZ равны нулю. Оставшиеся три уравнения явля-ются уравнениями равновесия параллельных сил в пространстве (рис. 1.34).

Для параллельных сил расположенных в плоскости XOY (рис. 1.35), имеем два уравнения равновесия:

Теорема Пуансо: Не изменяя действие силы на тело её можно перенести в любую точку тела добавив при атом пару сил с моментом, равным моменту переносимой силы относительно новой точки приложения.

10. Если силы, действующие на твердое тело, параллельны между собой, то можно выбрать такую систему координат, когда одна из ее осей, например Oz, параллельна направлению действия сил (рис.). Тогда из шести аналитических условий равновесия три выполняются тождественно, и система параллельных сил будет иметь только три условия равновесия:

Условия равновесия плоской системы сил.

Для плоской системы сил условия равновесия будут частным

, определяющих условия равновесия пространственной системы сил. Например, если силы расположены в плоскости Оху, то аналитические условия равновесия можно записать в виде:

Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из двух координатных осей и сумма алгебраических моментов этих сил относительно любого центра О были равны нулю. Алгебраическим моментом силы относительно точки называют момент силы относительно оси, проходящей через данную точку перпендикулярно плоскости, в которой расположена сила и точка .

Вместо иногда удобно применить условия равновесия в виде уравнений трех моментов: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы алгебраических моментов всех этих сил относительно любых трех центров А, В, С, не лежащих на одной прямой, были равны нулю:

равенствам .

13. Докажем следующую теорему Вариньона: момент равнодействующей плоской системы сходящихся сил относительно любого центра равен алгебраической сумме моментов слагаемых сил относительно того же центра.

Источник

Теоретическая механика

9. Плоская система сил. Пара сил. Момент пары сил.

Плоская система сил

Система сил, действующих на плоскости, называется плоской системой сил. Особенностью плоской системы сил заключается в том, что линии действия этих сил уже не пересекаются в одной точке.

Одним из важнейших понятий плоской системы сил является понятие пары сил.

Парой сил называется система двух, равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело.

Согласно аксиоме №1 пара сил не находится в равновесии и не имеет равнодействующую.

Вычисление алгебраического момента пары сил. Для вычисления алгебраического момента пары сил, удобно воспользоваться результатом следующей теоремы.

Теорема. Алгебраическая сумма моментов сил, составляющих пару, относительно любого центра, лежащего в плоскости действия пары сил не зависит от выбора этого центра. Момент пары сил равен произведению одной из сил, составляющих пару на плечо пары.

Пусть в плоскости действует пара сил, как показано на рис.С.24.

Тогда, согласно определению алгебраического момента пары сил и в соответствии с правилом знаков для момента силы относительно центра можно записать

Таким образом, алгебраический момент пары сил не зависит от расстояния до центра и равен произведению модуля силы на плечо пары.

Что и требовалось доказать.

В дальнейшем необходимо рассмотреть следующие теоремы, выражающие основные свойства пар сил и устанавливающие условие эквивалентности двух пар сил.

Теорема. Две пары сил, лежащие в одной плоскости и имеющие численно равные моменты и одинаковое направление вращения, эквивалентны.

Доказательство теоремы проведем в несколько этапов.

4. Согласно теореме Вариньона

Из доказанной теоремы вытекают два важных следствия.

Следствие 1. У данной пары сил, не изменяя оказываемого действия, можно менять величину и направление сил, а также длину плеча, сохраняя при этом величину момента силы.

Следствие 2. Данную пару сил, не изменяя оказываемого действия, можно переносить куда угодно в плоскости действия пары. Следовательно, действие пары на тело не зависит от положения пары в ее плоскости. Таким образом, момент пары является свободным вектором!

Источник

Теоремы об эквивалентности пар

Теоремы об эквивалентности пар

Теорема 1. Всякую пару, не изменяя ее действия на абсолютно твердое тело, можно заменить другой парой, расположенной как угодно в той же плоскости и имеющей одинаковое с данной парой направление вращения и равный по абсолютной величине момент.

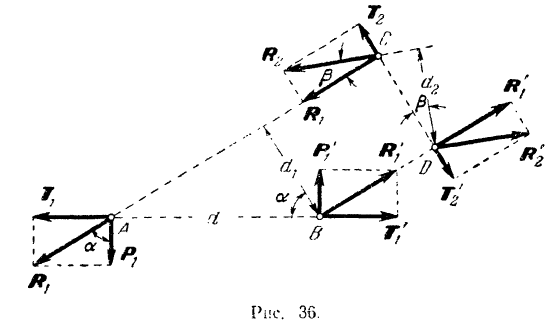
Доказательство. Пусть на тело действует пара

и две равные по модулю и направленные но одной прямой в противоположные стороны силы и . Складывая попарно силы и и силы и , мы, очевидно, придем к новой паре .Так как система сил — уравновешенная, то полученная пара эквивалентна данной.

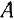
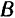
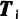
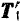
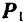
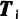
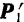
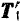
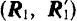
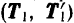
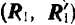
Если перенести силы этой пары в любые другие две точки, лежащие на линиях их действия (например, и , рис. 36) и вновь присоединить к силам данной пары любую уравновешенную систему сил то вновь будет получаться пара , эквивалентная данной:

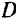
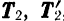
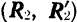
Нетрудно убедиться в том, что все полученные эквивалентные пары имеют одинаковое направление вращения (в данном случае противоположное ходу стрелки часов) и одинаковый по абсолютной величине момент.

В самом деле, как это видно из рис. 36,

Переносом сил пары по линиям их действия и повторением операций, подобных сделанным выше, можно, очевидно, перенести пару в любое положение в плоскости ее действия и любым образом изменять модули сил пары. При этом будет соответственно изменяться длина плеча пары, но модуль момента пары и направление ее вращения будут оставаться неизменными.

Как показывает опыт и как это доказывается в динамике, пара сил, как бы она не была расположена, всегда сообщает свободному телу вращение вокруг оси, проходящей через центр тяжести тела и перпендикулярной плоскости действия пары.

Нужно заметить, что перенос пары в ее плоскости действия, так же как и перенос силы по линии ее действия, безоговорочно применим лишь для абсолютно твердого тела. Мы можем пользоваться этим свойством пары при решении задач на равновесие внешних сил, приложенных и к деформируемому телу, так как это равновесие не нарушается от того, что такое тело станет абсолютно твердым (принцип отвердевания). Но деформация тела и возникающие в результате ее в теле внутренние силы, противодействующие этой деформации, зависят от места расположения пары, и поэтому в задачах сопротивления материалов всегда указывают сечение тела, на которое действует пара.

На рис. 37 в качестве примера изображены две балки, заделанные одним своим концом в стену и нагруженные парами. Ясно, что пара, приложенная к концевому сечению (рис. 37, о), будет деформировать (изгибать) всю балку, тогда как пара, приложенная к среднему сечению (рис. 37,6), будет изгибать только левую часть балки.

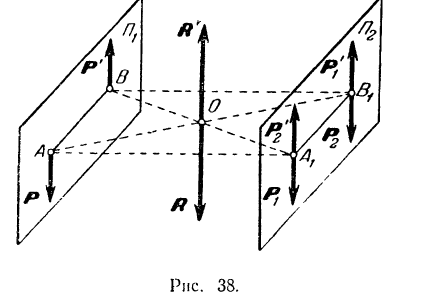
Теорема 2. Не изменяя действия пары на твердое тело, ее можно переносить в любую плоскость, параллельную плоскости действия данной пары.

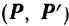
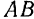
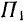
Доказательство. Пусть на тело действует пара с плечом , лежащая в плоскости (рис. 38).

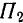
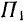
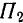
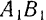
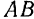
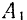
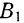
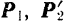
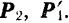
Предположим, что мы хотим эту пару перенести в какую-либо другую плоскость , связанную с данным телом и параллельную плоскости . Возьмем в плоскости отрезок и равный и параллельный отрезку

, и приложим в точках и по две взаимно уравновешивающиеся силы и . Эти силы возьмем параллельными силам заданной пары и равными им по модулю, так что

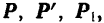
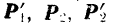
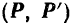
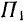
Так как добавленные силы взаимно уравновешиваются, то получившаяся система шести сил эквивалентна заданной паре , расположенной в плоскости .

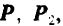
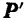
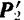
Но из новой системы шести сил четыре силы и также представляют собой уравновешенную систему и потому могут быть отброшены.

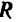
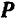
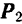
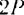
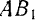
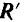
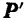
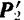
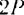
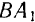
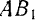
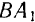
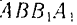
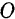
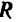
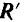
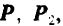
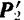
В самом деле, равнодействующая параллельных, направленных в одну сторону и равных сил и им параллельна, равна по модулю , направлена в ту же сторону и проходит через середину отрезка . Равнодействующая параллельных, направленных в одну сторону и равных сил и также им параллельна, равна по модулю , направлена в сторону действия этих сил и проходит через середину отрезка . Отрезки же и как диагонали параллелограмма , взаимно делятся пополам в точке их пересечения. Таким образом, равнодействующие и равны но модулю и направлены по одной прямой в противоположные стороны. Следовательно, эти равнодействующие взаимно уравновешиваются, и система сил (.) эквивалентна пулю.

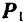
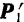
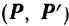
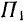
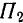
Остаются только две силы и , образующие пару, которая представляет собой, очевидно, заданную пару , перенесенную из плоскости в плоскость . Теорема доказана.

Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:

Возможно вам будут полезны эти дополнительные темы:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник