теорема ферма что это такое
Теорема Ферма
Существует Малая теорема Ферма́ и Великая теорема Ферма́.
Малая теорема Ферма: если p — простое число, то для любого целого числа a, не делящегося на p, делится на p число:
Великая теорема Ферма утверждает, что данная формула не имеет решений в натуральных числах x, y, z для n > 2 :
Доказательство Великой теоремы Ферма для всех простых чисел было найдено в 1993 году англо-американским математиком Сэром Эндрю Джоном Уайлсом (детально, формально и окончательно в 1995).
Применение уравнения Ферма (Великой теоремы Ферма): в процессе его изучения была создана вся система современного шифрования и кодирования (кодовые замки, банковские карты и т. д.).
Малая теорема Ферма
Малая теорема Ферма — это частный случай теоремы Эйлера и используется в элементарной теории чисел (это раздел теории чисел).
Малая теорема Ферма гласит, что если p — простое число, то для любого целого числа a, не делящегося на p, это число делится на p:
Формально Малая теорема Ферма часто обозначается так:
Это то же самое, что и предыдущая формулировка.
Пример Малой теоремы Ферма
Великая теорема Ферма
Уравнение Великой теоремы Ферма:
для n > 2, оно не имеет решений в натуральных числах x, y, z.
Для n = 2 мы знаем теорему Пифагора, где существует целое множество решений (формула c² = a² + b²), а с n > 2 многие самые великие умы математики боролись больше 300 лет, пока в 1993 году доказательство для всех n > 2 не было найдено Сэром Эндрю Джоном Уайлсом.
Узнайте подробнее про теорему Пифагора.
Доказательство Великой теоремы Ферма (Уайлса)
Доказательство Сэра Эндрю Джона Уайлса сформировано на идее изучения уравнений типа y² = x³ + αx + β. Оно даёт фигуру на графике примерно такой формы:
Потом изучается пересечение рациональных точек с этими графиками. Обе координаты должны являться дробями и две эти порождают третью, таким образом:
Кем был математик Ферма?
Француз Пьер де Ферма́ (1601–1665) по профессии был юристом, а математика была больше его увлечением. Он открыл основной принцип аналитической геометрии. Ферма является соучредителем теории вероятностей. Ещё он считается изобретателем дифференциального исчисления из-за его методов нахождения касательных к кривым и их точек максимума и минимума.
Существует легенда о том, что около 1630 года Ферма написал заметку примерно такого содержания на полях одной книги «Я обнаружил поистине замечательное доказательство, но поля книги слишком узки, чтобы его можно было вместить.»
Ферма великая теорема
Вели́кая теоре́ма Ферма́ (или последняя теорема Ферма) — одна из самых популярных теорем математики; её условие формулируется на понятийном уровне среднего общего образования, а доказательство теоремы искали многие математики более трёхсот лет. Окончательно доказана в 1995 году Уайлсом.
Содержание
Формулировка
Теорема утверждает, что:
История
Для случая n = 3 эту теорему в X веке пытался доказать среднеазиатский математик ал-Ходжанди, но его доказательство не сохранилось.
В общем виде теорема была сформулирована Пьером Ферма в 1637 на полях «Арифметики» Диофанта с припиской, что найденное им остроумное доказательство этой теоремы слишком длинно, чтобы его можно было здесь поместить:
Наоборот, невозможно разложить куб на два куба, биквадрат на два биквадрата и вообще никакую степень, большую квадрата, на две степени с тем же показателем. Я нашел этому поистине чудесное доказательство, но поля книги слишком узки для него.
Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duas ejusdem nominis fas est dividere; cujus rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.
Над полным доказательством Великой теоремы работало немало выдающихся математиков, и эти усилия привели к получению многих результатов современной теории чисел. Считается, что теорема стоит на первом месте по количеству неверных доказательств.
В 1908 году немецкий любитель математики Вольфскель завещал 100000 марок тому, кто докажет теорему Ферма. После Первой мировой войны премия обесценилась.
В 1980-х годах появился новый подход к решению проблемы. Из гипотезы Морделла, доказанной Фальтингсом в 1983 году, следует, что уравнение a n + b n = c n при n > 3 может иметь лишь конечное число взаимно простых решений.
Последний, но самый важный, шаг в доказательстве теоремы был сделан в сентябре 1994 года Уайлсом. Его 130-страничное доказательство было опубликовано в журнале «Annals of Mathematics». [2] Доказательство основано на предположении немецкого математика Герхарда Фрая о том, что Великая теорема Ферма является следствием гипотезы Таниямы — Симуры (это предположение было доказано Кеном Рибетом при участии Ж.‑П.Серра. [3] ).
Первый вариант своего доказательства Уайлс опубликовал в 1993 году (после 7 лет напряжённой работы), но в нём вскоре обнаружился серьёзный пробел; с помощью Ричарда Лоуренса Тейлора пробел удалось достаточно быстро ликвидировать. [4] В 1995 году был опубликован завершающий вариант. [5]
«Ферматисты»
Простота формулировки теоремы Ферма (доступная в понимании даже школьнику), а также сложность единственного известного доказательства (или неведение о его существовании), вдохновляют многих на попытки найти другое, более простое доказательство. Людей, вопреки здравому смыслу пытающихся доказать теорему Ферма элементарными методами, называют «ферматистами» или «ферматиками». [6] Ферматисты зачастую не владеют основами математической культуры и допускают ошибки в арифметических действиях или логических выводах, хотя некоторые представляют весьма изощренные «доказательства», в которых трудно найти ошибку. Положительным примером неудавшего доказательства теоремы Ферма могут служить результаты Куммера, которые хотя и содержали ошибку, в то же время дали толчок развитию алгебраической теории чисел.
Доказывать теорему Ферма в среде любителей математики было настолько популярно, что в 1972 году журнал «Квант», публикуя статью о теореме Ферма, сопроводил ее следующей припиской: [6]
Редакция «Кванта» со своей стороны считает необходимым известить читателей, что письма с проектами доказательств теоремы Ферма рассматриваться (и возвращаться) не будут.
Примечательно, что отдельные ферматисты добиваются публикации своих (неверных) «доказательств» в ненаучной прессе, которая раздувает их значение до научной сенсации. [7] [8]
Теорема Ферма в культуре и искусстве
См. также
Примечания
Литература
На русском
На английском
Полезное
Смотреть что такое «Ферма великая теорема» в других словарях:
Ферма великая теорема — утверждение П. Ферма о том, что диофантово уравнение (См. Диофантовы уравнения) xn + yn = zn, где n – целое число, большее двух, не имеет решений в целых положительных числах. Ф. в. т. установлена для ряда частных значений n, однако… … Большая советская энциклопедия
Ферма малая теорема — Малая теорема Ферма классическая теорема теории чисел, которая утверждает что Если p простое число и целое a не делится на p, то a p 1 ≡ 1 (mod p) (или a p 1 1 делится на p). Иная формулировка: Для любого простого … Википедия
ВЕЛИКАЯ ТЕОРЕМА ФЕРМА — ВЕЛИКАЯ ТЕОРЕМА ФЕРМА, гипотеза, впервые высказанная ФЕРМА, что для всех целых чисел n2 не существует таких натуральных чисел х, у и z, которые удовлетворяли бы уравнению хn+уn=zn. На полях одной из принадлежавших ему книг («Арифметика» Диофанта) … Научно-технический энциклопедический словарь
Великая теорема Ферма — Издание 1670 года «Арифметики» Диофанта включает комментарий Ферма, в частности его «последнюю теорему» (Observatio Domini Petri de Fermat). Великая теорема Ферма … Википедия
Ферма Пьер — Ферма (Fermat) Пьер (17.8.1601, Бомон де Ломань, √ 12.1.1665, Кастр), французский математик. По профессии юрист: с 1631 был советником парламента в Тулузе. Автор ряда выдающихся работ, большинство из которых было издано после смерти Ф. его сыном … Большая советская энциклопедия
Теорема Ферма — Теоремы Ферма были сформулированы Пьером Ферма: Великая теорема Ферма Малая теорема Ферма Лемма Ферма о локальном экстремуме … Википедия
Ферма — I Ферма (Fermat) Пьер (17.8.1601, Бомон де Ломань, – 12.1.1665, Кастр), французский математик. По профессии юрист: с 1631 был советником парламента в Тулузе. Автор ряда выдающихся работ, большинство из которых было издано после смерти Ф.… … Большая советская энциклопедия
ФЕРМА ТЕОРЕМА — великая теорема Ферма, знаменитая теорема Ферма, большая теорема Ферма, последняя теорема Ферма, утверждение, что для любого натурального числа п>2 уравнение xn+yn=zn (уравнение Ферма) не имеет решений в целых ненулевых числах х, у, z. Она была… … Математическая энциклопедия
ФЕРМА — • ФЕРМА (Fermat) Пьер де (1601 65), французский математик. Вместе с Блезом ПАСКАЛЕМ сформулировал теорию вероятности и, доказав, что свет перемещается по самой короткой оптической траектории (принцип Ферма), стал основателем геометрической оптики … Научно-технический энциклопедический словарь
ТЕОРЕМА — ТЕОРЕМА, утверждение или предложение, которое доказывается логическими рассуждениями, основанными на фактах и АКСИОМАХ. см. также ВЕЛИКАЯ ТЕОРЕМА ФЕРМА … Научно-технический энциклопедический словарь
Великая теорема Ферма
Вели́кая теоре́ма Ферма́ (или Последняя теорема Ферма) — одна из самых популярных теорем математики. Её условие формулируется на понятийном уровне среднего общего образования, а доказательство теоремы искали многие математики более трёхсот лет. Окончательно доказана в 1995 году Эндрю Уайлсом.
Содержание
Формулировка
Теорема утверждает, что:
Для любого натурального числа
2″ border=»0″ /> уравнение
не имеет натуральных решений 


История
Для случая 
В общем виде теорема была сформулирована Пьером Ферма в 1637 году на полях «Арифметики» Диофанта. Дело в том, что Ферма делал свои пометки на полях читаемых математических трактатов и там же формулировал пришедшие на ум задачи и теоремы. Теорему, о которой ведётся речь, он записал с припиской, что найденное им остроумное доказательство этой теоремы слишком длинно, чтобы его можно было поместить на полях книги:
Наоборот, невозможно разложить куб на два куба, биквадрат на два биквадрата и вообще никакую степень, большую квадрата, на две степени с тем же показателем. Я нашел этому поистине чудесное доказательство, но поля книги слишком узки для него.
Cubum autem in duos cubos, aut quadrato-quadratum in duos quadrato-quadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duas ejusdem nominis fas est dividere; cujus rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.
Несколько позже сам Ферма опубликовал доказательство частного случая для 
Над полным доказательством Великой теоремы работало немало выдающихся математиков и множество дилетантов-любителей; считается, что теорема стоит на первом месте по количеству некорректных «доказательств». Тем не менее эти усилия привели к получению многих важных результатов современной теории чисел. Давид Гильберт в своём докладе «Математические проблемы» на II Международном конгрессе математиков (1900) так отозвался об этой проблеме [2] :
Проблема доказательства этой неразрешимости являет разительный пример того, какое побуждающее влияние на науку может оказать специальная и на первый взгляд малозначительная проблема. Ибо, побуждённый задачей Ферма, Куммер пришёл к введению идеальных чисел и к открытию теоремы об однозначном разложении чисел в круговых полях на идеальные простые множители — теоремы, которая теперь, благодаря обобщениям на любую алгебраическую числовую область, полученным Дедекиндом и Кронекером, является центральной в современной теории чисел и значение которой выходит далеко за пределы теории чисел в область алгебры и теории функций.
В 1908 году немецкий любитель математики Вольфскель завещал 100 000 немецких марок тому, кто докажет теорему Ферма. Однако после Первой мировой войны премия обесценилась.
В 1980-х годах появился новый подход к решению проблемы. Из гипотезы Морделла, доказанной Фальтингсом в 1983 году, следует, что уравнение 

«Ферматисты»
Простота формулировки теоремы Ферма (доступная в понимании даже школьнику), а также сложность единственного известного доказательства (или неведение о его существовании), вдохновляют многих на попытки найти другое, более простое, доказательство. Людей, пытающихся доказать теорему Ферма элементарными методами, называют «ферматистами» или «ферматиками». [7] Ферматисты зачастую не владеют основами математической культуры и допускают ошибки в арифметических действиях или логических выводах, хотя некоторые представляют весьма изощренные «доказательства», в которых трудно найти ошибку.
Доказывать теорему Ферма в среде любителей математики было настолько популярно, что в 1972 году журнал «Квант», публикуя статью о теореме Ферма, сопроводил ее следующей припиской: [7]
 | Редакция «Кванта» со своей стороны считает необходимым известить читателей, что письма с проектами доказательств теоремы Ферма рассматриваться (и возвращаться) не будут. |  |
Немецкому математику Эдмунду Ландау очень докучали «ферматисты». Чтобы не отвлекаться от основной работы, он заказал несколько сот бланков со следующим текстом:
 | Уважаемый …! Благодарю Вас за присланную Вами рукопись с доказательством Великой теоремы Ферма. Первая ошибка находится на стр. … в строке … |  |
Находить ошибку и заполнять пробелы в бланке он поручал своим аспирантам.
Примечательно, что отдельные ферматисты добиваются публикации своих (неверных) «доказательств» в ненаучной прессе, которая раздувает их значение до научной сенсации. [8] [9] Впрочем, иногда такие публикации появляются и в уважаемых научных изданиях, [10] как правило, с последующими опровержениями. [11] Среди других примеров:
Теорема Ферма в культуре и искусстве
Великая теорема Ферма стала символом труднейшей научной проблемы и в этом качестве часто упоминается в беллетристике. Далее перечислены некоторые произведения, в которых теорема не просто упомянута, но является существенной частью сюжета или идеологии произведения.
Почему доказательство Великой теоремы Ферма не нуждается в улучшениях
В течение десятилетий, прошедших после появления знакового доказательства великой теоремы Ферма, появилось несколько идей по поводу того, как сделать его ещё более надёжным. Однако эти попытки отражают глубокое непонимание того, что делает доказательство важным.
23 июня исполнилось 25 лет с момента взбудоражившего всех объявления от Эндрю Уайлса, в котором он заявил о получении доказательства великой теоремы Ферма – наиболее известной в математике задачи возрастом 350 лет. История, окружающая доказательство Уайлса – семь лет он тайно работал над этим проектом, разрыв в доказательстве, обнаружившийся после июньского объявления, элегантное решение, опубликованное год спустя в совместной работе, написанной Уайлсом вместе с его бывшим студентом Ричардом Тэйлором, получение рыцарского звания в 2000 – вошло в анналы математических легенд.
После прорыва Уайлса часто можно услышать рассуждения о наступлении новой «золотой эры» в математике, особенно в теории чисел – области, к которой и принадлежит теорема Ферма. Методы, представленные Уайлсом и Тейлором, сегодня являются частью инструментария специалистов по теории чисел, считающих историю Великой теоремы закрытой. Но эта история тронула не только специалистов по теории чисел.
Мне неожиданно напомнили об этом события 2017 года, когда в промежуток из нескольких дней два логика, делавших доклад на двух разных континентах, указали на способы улучшения доказательства Теоремы – и рассказали о том, насколько удивились их коллеги, когда специалисты по теории чисел не выказали к их идеям никакого интереса.
Логики выражали эти идеи на языках своих соответствующих специальностей – теории множеств и теоретической информатики. Сделанные ими предложения по сути своей были истинными, и, возможно, когда-нибудь поднимут новые вопросы, не менее интересные, чем у Ферма. Однако мне сразу же стало ясно, что эти вопросы не имеют отношения к специалистам по теории чисел, и любые иные предположения отражают глубокое непонимание природы доказательства Уайлса и целей теории чисел в целом.
Корни этого непонимания можно обнаружить в простоте утверждения Теоремы, которая и отвечает за большую часть её привлекательности: если n – любое положительное целое число, большее 2, то невозможно найти три таких положительных числа, a, b и c, что:
Однако математики никогда не записывают доказательства таким способом. Логический анализ доказательства Уайлса указывает на множество шагов, не учитывающих ZFC, тая в себе потенциал для скандала: если математики придумывают правила, не проверяя их на конституционность, откуда они знают, что все они имеют в виду одно и то же?
Автоматическая проверка доказательств, кажется, предлагает решение этой проблемы. Она подразумевает переформулировку доказательства через набор раздельных заявлений, каждое из которых записано непротиворечивым языком, который компьютер может считать, а затем и подтвердить конституционную верность каждого шага. Этот трудоёмкий метод с успехом применялся ко многим длинным и сложным доказательствам, наиболее известное из которых – доказательство гипотезы Кеплера о наиплотнейшей упаковке сфер, сделанное Томасом Хейлсом. Проверка доказательства Уайлса давно считалась одной из главных целей. Поэтому мой друг, специалист по информатике, был искренне разочарован, что поиски «чистых математиков, безапелляционно поддерживающих использование автоматических инструментов в построении их аргументов», как он это сформулировал, пока не дают результатов.

«Арифметика» Диофанта издания 1670 года, в котором в основной текст включена и печально известная заметка Ферма. В переводе она звучит так: «Кубу невозможно быть суммой двух кубов, четвёртой степени невозможно быть суммой двух четвёртых степеней, или, в общем, любому числу, представляющему собою степень, большую второй, невозможно быть суммой двух таких же степеней. Я открыл воистину чудесное доказательство этого предположения, для размещения которого здесь эти поля слишком узки».
Первое, что не учитывает это разочарование — что доказательство Уайлса, пусть сложное, имеет простую основу, которую легко объяснить обывательской аудитории. Допустим, что, в противоречие с утверждением Ферма, существует тройка положительных целых чисел a, b, c таких, что
для некоего нечётного простого p (а достаточно рассматривать только простые числа). В 1985 году Герхард Фрей показал, что a, b и c можно перегруппировать в
(B) новое уравнение, под названием «эллиптическая кривая»
со свойствами, которые, как все считали, невозможны. Точнее говоря, уже давно было известно, как выразить эту эллиптическую кривую через
(С) представление Галуа
которое является бесконечным набором уравнений, связанных как с эллиптической кривой, так и друг с другом чёткими правилами.
Связь между этими шагами была хорошо известна в 1985 году. К тому времени большинство специалистов по теории чисел были убеждены – хотя доказательства пока не было – что каждому представлению Галуа можно назначить, опять-таки, по чётким правилам,
(D) модулярную функцию,
что-то вроде двумерного обобщения знакомых из тригонометрии функций синуса и косинуса.
Итоговое звено было получено, когда Кен Рибет подтвердил предположение Жан-Пьера Сера о том, что свойства модулярной функции, заданные формой эллиптической кривой Фрея, подразумевают существование
(E) ещё одной модулярной функции веса 2 и уровня 2.
Однако таких функций существовать не может. Следовательно, не существует ни модулярной функции (D), ни представления Галуа (С), ни уравнения (B), ни решения (A).
Оставалось лишь найти отсутствующее звено между (С) and (D), которое математики назвали гипотезой модулярности.
Это звено было объектом семилетних поисков Уайлса. С нашей текущей точки зрения тяжело в полной мере оценить отважность этого рискованного предприятия. Через двадцать лет после того, как Ютака Танияма и Горо Шимура в 1950-х впервые сообщили о связи между (B) и (D) через (С), математики постепенно пришли к выводу, что это должно быть так. Именно эту надежду высказал в очень популярной работе Андре Вейл, которая идеально вписалась в крайне влиятельную программу Ленглендса, названную в честь канадского математика Роберта Ленглендса. Эта связь была слишком хорошей для того, чтобы не быть правдой. Однако гипотеза модулярности казалась совершенно недостижимой. Объекты типов (С) и (D) были слишком разными.
Специалист по информатике не пояснил, связано ли его разочарование с тем, что специалистам по теории чисел было неважно, что доказательство было ограничено поисками критически важного звена между (С) и (D), или что оно простиралось на всём промежутке от (A) до (E). Не буду пытаться разобраться в этом. Но если логикам нужно было только формально подтвердить опубликованное доказательство связи между (С) и (D), то их ожидания были слишком завышенными. Во-первых, Уайлс доказал лишь чуть более, чем достаточно для того, чтобы гипотеза модулярности завершала дедукцию «от (A) до (E)». Полную гипотезу модулярности установили несколько лет спустя Кристоф Бройль, Брайан Конрад, Фред Даймонд и Ричард Тэйлор. Но это не бросает тень на работу Уайлса! Наоборот, то, что такое большое количество ведущих мировых специалистов по теории чисел пошли по стопам работы Уайлса всего через несколько месяцев после её появления, говорит о её богатстве.
К примеру, чуть позже, осенью 2016 года, 10 математиков встретились в Институте передовых исследований в Принстоне, Нью-Джерси, и смогли доказать наличие связи между эллиптическими кривыми и модулярными функциями в новых условиях. Все они использовали разные пути для понимания структуры доказательства Уайлса, появившегося, когда некоторые из них ещё были детьми. Если бы их попросили описать это доказательство в виде последовательности логических выводов, они, несомненно, выдали бы 10 разных его вариантов. Каждый из них напоминал бы путь от (A) до (E), описанный выше, но был бы гораздо более детальным.
Тем не менее – и это всегда упускают из философского взгляда на доказательства – каждый из этих десяти приписал бы авторство своего доказательства Уайлсу. Они бы ссылались на них тем же образом, что и на другие доказательства, изучаемые ими в разъяснительных статьях или на учебных курсах, которые они посещали или которые преподавали. И хотя каждый из десяти опустил бы какие-нибудь детали, в целом все они были бы правы.
Что же такое доказательства Уайлса, если оно может иметь так много разных вариантов? В математической философии принято относиться к опубликованному доказательству, как к приближению к идеальному формализованному доказательству, которое в принципе можно проверить на компьютере, применяющем правила формальной системы. Идеальное доказательство не загрязняется ничем, что находится за пределами формальной системы – так, будто бы каждый закон нёс на себе метку, подтверждающую его конституциональную оправданность.
Но такой подход противоречит тому, что сами математики говорят о своих доказательствах. Математики не применяют идеологических или философских лакмусовых тестов, но я убеждён, что большинство моих коллег согласятся с Майклом Фрэнсисом Атья, заявившим, что доказательство – «это итоговая проверка, но не основа чего-либо». Опубликованное доказательство явно не является основой чего-либо.
Уайлс и специалисты по теории чисел, уточнявшие и расширявшие его идеи, несомненно не ожидали получить предложения от двух логиков. Но – в отличие от многих людей, наблюдающих за теорией чисел издалека – они определённо понимали, что к такому доказательству, как к тому, что опубликовал Уайлс, не стоит относиться, как к некоему артефакту в себе. Наоборот, доказательство Уайлса – это стартовая точка открытого диалога, который является слишком неуловимым и живым, чтобы ограничивать его серьёзными пределами, чуждыми данной теме.






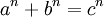


 2″ border=»0″ /> уравнение
2″ border=»0″ /> уравнение

