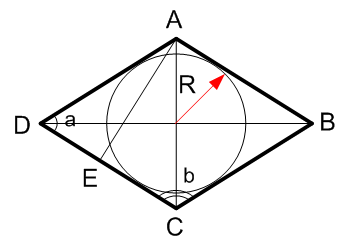
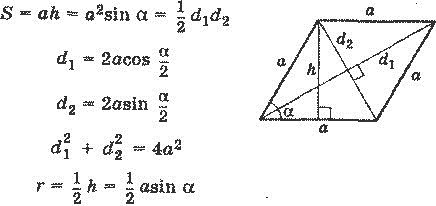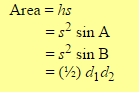Как узнать высоту ромба
Сторона и высота ромба
Свойства
Ромб – это геометрическая фигура, у которой все стороны равны, поэтому ее периметр, как и периметр квадрата равен стороне, умноженной на 4. Площадь ромба зависит не только от его стороны, но и высоты, так как ромб является параллелограммом, эта формула заимствована от него. Чтобы вычислить площадь ромба необходимо умножить высоту на его сторону. P=4a S=ah
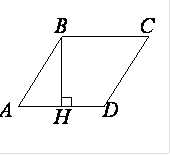
Углы ромба также связаны с высотой, так как она образует внутри ромба прямоугольный треугольник. Синус угла α в ромбе равен отношению высоты, как катета, к стороне ромба, как гипотенузе. Угол β можно найти через разность 180 градусов и угла α. (рис.115.1) sinα=h/a β=180°-α
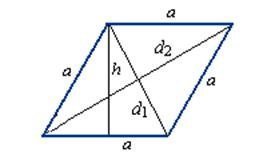
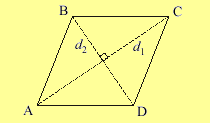
Зная любой угол ромба, можно найти его диагонали. Поскольку диагонали ромба пересекаются под прямым углом, они делят ромб на четыре конгруэнтных прямоугольных треугольника, катетами которых являются половины диагоналей и гипотенузой – сторона ромба. Соответственно в каждом таком треугольнике, углы равны половинам углов ромба. Вычислить диагонали через угол α можно, приравняв их к стороне ромба умноженной на синус или косинус α соответственно. (рис.115.2) d_1=a sin〖α/2〗 d_1=a cos〖α/2〗
Так как ромб является равносторонним многоугольником, следовательно, в него можно вписать окружность. Радиус вписанной окружности соединяет ее центр в точке пересечения диагоналей и сторону ромба перпендикулярным ей отрезком. Поскольку единственным перпендикуляром в ромбе является высота, то в совокупности с вышеописанным свойствами можно сделать вывод, что радиус равен половине высоты ромба. (рис.115.3) r=h/2
Чему равна высота ромба по формуле?
В школе учили чему равна высота ромба. А теперь, когда нужно, забыла формулы по которым можно посчитать высоту ромба. Пожалуйста подскажите, какие существуют формулы для расчета высоты?
Варианты определения высоты
Если вам известно, чему равна сторона ромба (обозначается буквой а) и его площадь (S), вычислить высоту можно по простой формуле: h=S:a. Основная формула служит для определения площади: S=a*h.
Если для определения высоты по указанной выше формуле у вас не достает данных, вы можете воспользоваться некоторыми другими. Найдя с их помощью нужные значения, вы сможете подставить их в ту, по которой можно определить высоту.
Если вам известна длина диагоналей, вы легко найдете площадь. S=(d1*d2)/2.
Зная периметр ромба, можно найти длину его стороны: P=4a.
Еще одна формула для определения площади. S=a*a*sin (a).
Важно: существуют еще более сложные формулы, которые помогут определить дополнительные параметры. Как правило, в школьных задачах никто не предоставляет данные, по которым легко определить высоту ромба. Чтобы дать правильный ответ на поставленный вопрос, требуется применение нескольких формул. Совет: нарисуйте небольшую шпаргалку (ромб с обозначение сторон + формулы).
Как найти высоту ромба, если известны диагонали?
Чтобы вычислить высоту, нам придется посчитать площадь ромба и размер одного катета (в ромбе, как известно, они одинаковые).
Итак, наши действия:
Как найти высоту ромба, если известна площадь и периметр (какая формула)?
Ознакомьтесь со всеми формулами расчета площади ромба:
Чтобы узнать высоту, нам нужна самая первая формула (Площадь = Высота умножить на Длину стороны).
Чтобы подсчитать высоту ромба, нужно узнать размер катета. Вот какие действия помогут в решение задачи:
Как найти высоту ромба, если известна сторона и угол?
Чтобы посчитать размер высоты, используем формулу площади ромба (сторона в квадрате умножить на синус угла). Чтобы узнать синус любого градуса, воспользуйтесь таблицей в моем ответе. Синус 90 градусов равняется 1, потому найти высоту будет очень просто. Получается, что площадь равна квадрату длины стороны (3) умножить на синус 90 гр. (1), что в итоге дает ответ- 3 см кв.
Как посчитать высоту ромба, если известна сторона и диагональ?
В этой задаче нужно использовать прямоугольный треугольник, который образован пересечением диагоналей.
Высота ромба онлайн
С помощю этого онлайн калькулятора ромба можно найти высоту ромба по известным элементам. Для нахождения высоты ромба введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.
| Открыть онлайн калькулятор |
1. Высота ромба через сторону и площадь
Пусть задан ромб (Рис.1).
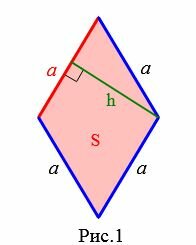 |
Формула площади ромба через сторону и высоту имеет следующий вид:
Откуда легко вывести формулу высоты ромба через сторону и площадь:
2. Высота ромба через сторону и угол
Рассмотрим ромб со стороной a и углом α между сторонами (Рис.2). Выведем формулу вычисления высоты ромба через сторону и угол.
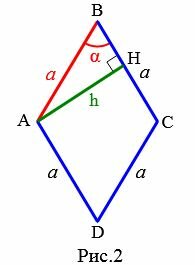 |
Проведем высоту AH. Для прямоугольного треугольника AHB применим теорему синусов:
Откуда получим формулу вычисления высоты ромба через сторону и угол между сторонами:
Заметим, что формула (2) справедлива для любого угла ромба, как для острого, так и для тупого угла. Действительно. Из четвертого свойста ромба (см. статью Ромб) следует, что сумма соседних углов ромба равна 180°. Тогда для угла C можно записать: \(\small \angle C=180°-\alpha.\) Следовательно \(\small \sin \angle C=\sin(180°-\alpha)=\sin \alpha.\) Получили, что синусы углов ромба равны. Поэтому в качестве угла между сторонами ромба можно выбрать любой угол ромба.
3. Высота ромба через диагонали
Выведем формулу вычисления высоты ромба через диагонали. Плошадь ромба через диагонали вычисляется формулой (см. статью Площадь ромба):
а через сторону и высоту, формулой
Из формул (3) и (4) следует:
Выразим сторону a ромба через диагонали. Поскольку диагонали ромба перпендикулярны и делятся пополам точкой их пересечения (свойства 5 и 6 ромба), то диагонали делят ромб на четыре равных прямоугольных треугольника (Рис.3).
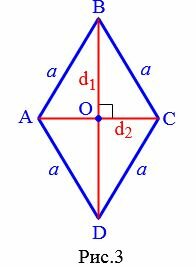 |
Применим к прямоугольному треугольнику AOB теорему Пифагора:
Подставим (7) в (5) и найдем h:
4. Высота ромба через угол и противолежащую диагональ
Пусть известны один из углов α=∠ABC ромба и противолежащая диагональ d=AC (Рис.4). Выведем формулу вычисления высоты ромба.
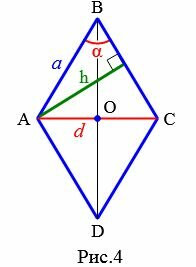 |
Проведем другой диагональ BD. Как было отмечено выше, диагонали ромба разделяют его на четыре равных прямоугольных треугольников. Применим теорему синусов для прямоугольного треугольника AOB:
С другой стороны (см. параграф 2):
Применяя формулу двойного угла для \(\small \sin \alpha, \) имеем: \(\small \sin \alpha=2 \cdot \sin \frac<\alpha> <2>\cdot \cos \frac<\alpha> <2>. \) Подставляя это равенство в формулу (11), получим формулу высоты ромба через угол и противолежащую диагональ:
5. Высота ромба через угол и диагональ из данного угла
Пусть известны один из углов α=∠ABC ромба и диагональ из данного угла d=BD (Рис.5). Выведем формулу вычисления высоты ромба.
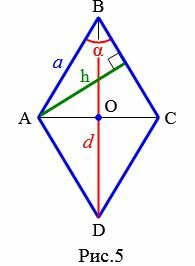 |
Проведем другой диагональ AC. Как было отмечено в выше, диагонали ромба разделяют его на четыре равных прямоугольных треугольников. Для прямоугольного треугольника AOB, имеем:
Учитывая, что \( \small BO=\frac<\large d><\large 2>\) и \( \small \angle ABO=\frac<\large \alpha><\large 2>\), формулу (13) можно записать так:
или, учитывая что \(\small \sin \alpha=2 \cdot \sin \frac<\alpha> <2>\cdot \cos \frac<\alpha> <2>, \) получим:
6. Высота ромба через радиус вписанной в ромб окружности
Покажем, что высота ромба через радиус вписанной окружности вычисляется по формуле:
В статье Площадь ромба показали, что площадь ромба через сторону и высоту вычисляется формулой
а площадь ромба через сторону и радиус вписанной окружности − формулой:
Формулы ромба
Для расчёта всех основных параметров ромба воспользуйтесь калькулятором.
Свойства ромба
Признаки ромба
Формулы стороны ромба
Длина стороны ромба через площадь (S) и высоту (AE)
Длина стороны ромба через площадь (S) и синус угла
Длина стороны ромба через диагонали
Длина стороны ромба через диагональ и угол
Длина стороны ромба через периметр
Формулы диагоналей ромба
Длина большой диагонали ромба через сторону и косинус острого угла(∠CDA) или косинус тупого угла(∠DAB)
Длина малой диагонали ромба через сторону и косинус острого угла(∠CDA) или косинус тупого угла(∠DAB)
Длина диагонали ромба через сторону и другую диагональ
Длина диагонали ромба через площадь и другую диагональ
Длина диагонали ромба через тангенс острого tg(∠CDA) или тупого tg(∠DAB) угла и другую диагональ
Формулы площади ромба
Площадь ромба через высоту (AE) и сторону
Площадь ромба через сторону и синус любого угла
Площадь ромба через две диагонали
Площадь ромба через большую диагональ и тангенс острого угла(∠CDA) или малую диагональ и тангенс тупого угла(∠DAB)
Формулы радиуса круга вписанного в ромб
Радиус вписанного круга в ромб через высоту ромба (AE)
Радиус вписанного круга в ромб через площадь и сторону ромба
Радиус вписанного круга в ромб через сторону и синус любого угла
Радиус вписанного круга в ромб через диагональ и синус угла
Радиус вписанного круга в ромб через две диагонали
Ромб. Формулы, признаки и свойства ромба
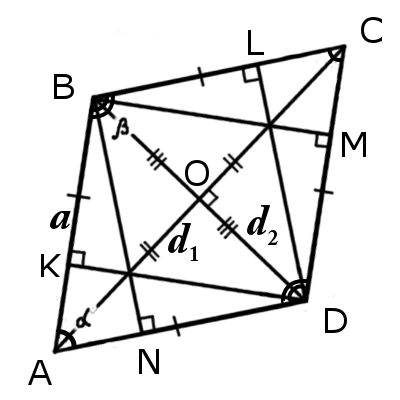 | 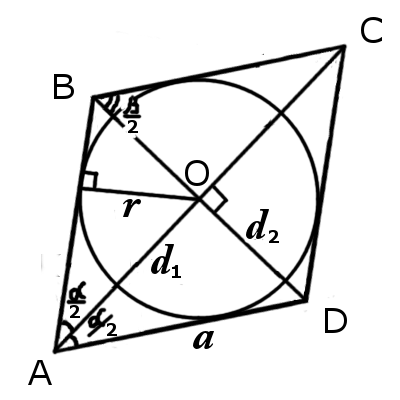 |
| Рис.1 | Рис.2 |
Признаки ромба
∠BAC = ∠CAD или ∠BDA = ∠BDC
Δ ABO = Δ BCO = Δ CDO = Δ ADO
Основные свойства ромба
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
Сторона ромба
Формулы определения длины стороны ромба:
2. Формула стороны ромба через площадь и синус угла:
| a = | √ S |
| √ sinα |
| a = | √ S |
| √ sinβ |
3. Формула стороны ромба через площадь и радиус вписанной окружности:
| a = | S |
| 2 r |
6. Формула стороны ромба через большую диагональ и половинный угол:
| a = | d 1 |
| 2 cos ( α /2) |
| a = | d 1 |
| 2 sin ( β /2) |
7. Формула стороны ромба через малую диагональ и половинный угол:
| a = | d 2 |
| 2 cos ( β /2) |
| a = | d 2 |
| 2 sin ( α /2) |
Диагонали ромба
Формулы определения длины диагонали ромба:
d 1 = a √ 2 + 2 · cosα
d 2 = a √ 2 + 2 · cosβ
d 1 = 2 a · cos ( α /2)
d 1 = 2 a · sin ( β /2)
d 2 = 2 a · sin ( α /2)
d 2 = 2 a · cos ( β /2)
7. Формулы диагоналей через площадь и другую диагональ:
| d 1 = | 2S |
| d 2 |
| d 2 = | 2S |
| d 1 |
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
| d 1 = | 2 r |
| sin ( α /2) |
| d 2 = | 2 r |
| sin ( β /2) |
Периметр ромба
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Площадь ромба
Формулы определения площади ромба:
4. Формула площади ромба через две диагонали:
5. Формула площади ромба через синус угла и радиус вписанной окружности:
6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):
| S = | 1 | d 1 2 · tg ( α /2) |
| 2 |
| S = | 1 | d 2 2 · tg ( β /2) |
| 2 |
Окружность вписанная в ромб
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
| r = | a · sinα |
| 2 |
| r = | a · sinβ |
| 2 |
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
| r = | d 1 · sin ( α /2) |
| 2 |
| r = | d 2 · sin ( β /2) |
| 2 |
6. Формула радиуса круга вписанного в ромб через две диагонали:
| r = | d 1 · d 2 |
| 2√ d 1 2 + d 2 2 |
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.