Как узнать сложность алгоритма
Оценка сложности алгоритмов, или Что такое О(log n)
Авторизуйтесь
Оценка сложности алгоритмов, или Что такое О(log n)
Наверняка вы не раз сталкивались с обозначениями вроде O(log n) или слышали фразы типа «логарифмическая вычислительная сложность» в адрес каких-либо алгоритмов. И если вы хотите стать хорошим программистом, но так и не понимаете, что это значит, — данная статья для вас.
Оценка сложности
Сложность алгоритмов обычно оценивают по времени выполнения или по используемой памяти. В обоих случаях сложность зависит от размеров входных данных: массив из 100 элементов будет обработан быстрее, чем аналогичный из 1000. При этом точное время мало кого интересует: оно зависит от процессора, типа данных, языка программирования и множества других параметров. Важна лишь асимптотическая сложность, т. е. сложность при стремлении размера входных данных к бесконечности.
Примеры
O(n) — линейная сложность
Такой сложностью обладает, например, алгоритм поиска наибольшего элемента в не отсортированном массиве. Нам придётся пройтись по всем n элементам массива, чтобы понять, какой из них максимальный.
O(log n) — логарифмическая сложность
Простейший пример — бинарный поиск. Если массив отсортирован, мы можем проверить, есть ли в нём какое-то конкретное значение, методом деления пополам. Проверим средний элемент, если он больше искомого, то отбросим вторую половину массива — там его точно нет. Если же меньше, то наоборот — отбросим начальную половину. И так будем продолжать делить пополам, в итоге проверим log n элементов.
O(n 2 ) — квадратичная сложность
20–22 декабря, Онлайн, Беcплатно
Бывают и другие оценки по сложности, но все они основаны на том же принципе.
Аналогично проводят оценку и по памяти, когда это важно. Однако алгоритмы могут использовать значительно больше памяти при увеличении размера входных данных, чем другие, но зато работать быстрее. И наоборот. Это помогает выбирать оптимальные пути решения задач исходя из текущих условий и требований.
Наглядно
Время выполнения алгоритма с определённой сложностью в зависимости от размера входных данных при скорости 10 6 операций в секунду:
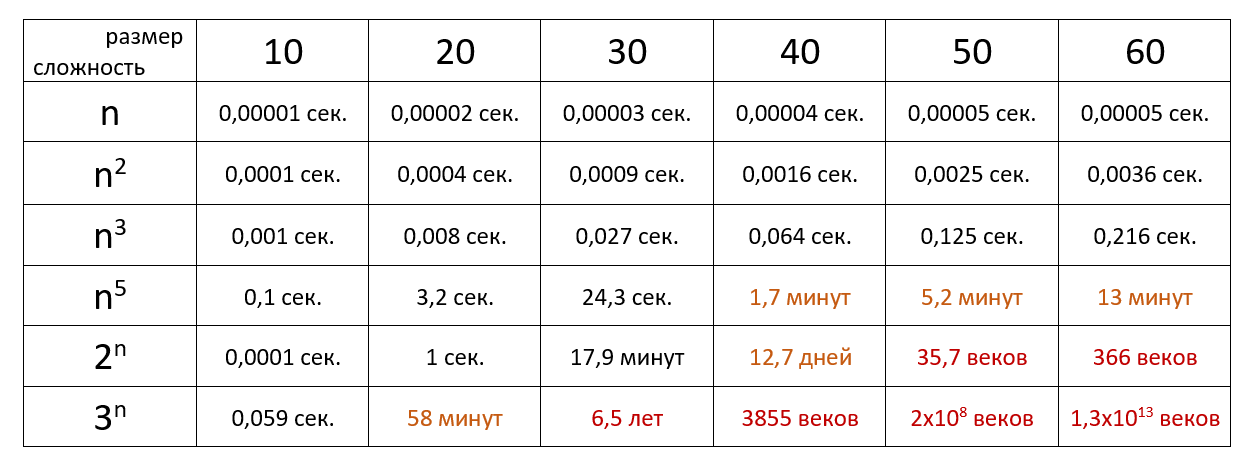
Если хочется подробнее и сложнее, заглядывайте в нашу статью из серии «Алгоритмы и структуры данных для начинающих».
Введение в анализ сложности алгоритмов (часть 2)
От переводчика: данный текст даётся с незначительными сокращениями по причине местами излишней «разжёванности» материала. Автор абсолютно справедливо предупреждает, что отдельные темы могут показаться читателю чересчур простыми или общеизвестными. Тем не менее, лично мне этот текст помог упорядочить имеющиеся знания по анализу сложности алгоритмов. Надеюсь, что он окажется полезен и кому-то ещё.
Из-за большого объёма оригинальной статьи я разбила её на части, которых в общей сложности будет четыре.
Я (как всегда) буду крайне признательна за любые замечания в личку по улучшению качества перевода.
Сложность
Такой метод поиска значения внутри массива называется линейным поиском. Это обоснованное название, поскольку программа имеет f( n ) = n (что означает «линейный» более точно, мы рассмотрим в следующем разделе). Инструкция break позволяет программе завершиться раньше, даже после единственной итерации. Однако, напоминаю, что нас интересует самый неблагоприятный сценарий, при котором массив A вообще не содержит заданное значение. Поэтому f( n ) = n по-прежнему.
Давайте рассмотрим программу на Python, которая складывает два значения из массива и записывает результат в новую переменную:
Следующая программа на C++ проверяет, содержит ли вектор (своеобразный массив) A размера n два одинаковых значения:
Нотация «большое О»
В реальной жизни иногда проблематично выяснить точное поведение алгоритма тем способом, который мы рассматривали выше. Особенно для более сложных примеров. Однако, мы можем сказать, что поведение нашего алгоритма никогда не пересечёт некой границы. Это делает жизнь проще, так как чёткого указания на то, насколько быстр наш алгоритм, у нас может и не появиться, даже при условии игнорирования констант (как раньше). Всё, что нам нужно — найти эту границу, а как это сделать — проще объяснить на примере.
Наиболее известной задачей, которую используют при обучении алгоритмам, является сортировка. Даётся массив A размера n (звучит знакомо, не так ли?), и нас просят написать программу, его сортирующую. Интерес тут в том что, такая необходимость часто возникает в реальных системах. Например, обозревателю файлов нужно отсортировать файлы по имени, чтобы облегчить пользователю навигацию по ним. Или другой пример: в видеоигре может возникнуть задача сортировки 3D объектов, демонстрируемых на экране, по их расстоянию от точки зрения игрока в виртуальном мире. Цель: определить, какие из них будут для него видимы, а какие — нет (это называется Visibility Problem). Сортировка также интересна тем, что для неё существует множество алгоритмов, одни из которых хуже, чем другие. Так же эта задача проста для определения и объяснения. Поэтому давайте напишем кусок кода, который будет сортировать массив.
Перед вами совершенно неэффективный способ реализации сортировки массива на Ruby. (Конечно, Ruby поддерживает сортировку массивов с использованием встроенных функций, которые и следует использовать. Они несомненно быстрее, чем код выше, представленный исключительно для иллюстрации.)
Заметьте также, что хотя Ω и даёт нам нижний предел поведения нашей функции (т.е. мы улучшаем программу, чтобы она вычисляла меньшее количество инструкций), мы всё ещё ссылаемся на анализ наихудшего случая. Это происходит потому, что мы подаём на вход программы наихудший набор данных и анализируем её поведение.
В следующей таблице собраны символы, которые мы представили выше, и их связь с обычными математическими значками для сравнения чисел. Причина, по которой мы пользуемся греческими буквами вместо привычной математической нотации, в необходимости показать, что мы имеем дело со сравнением асимптотических оценок, а не с обычным.
| Оператор сравнения асимптотических оценок | Оператор сравнения чисел |
|---|---|
| Алгоритм является o( что-то ) | Число чего-то |
Экспресс-оценка сложности алгоритма (+разбор задачи c Joker 2017 и DotNext 2017 Moscow)
Для любого практического применения log(n) можно считать константой. Просто в некоторых компаниях эта константа больше, чем у вас. © народная мудрость
Половину жизни я учу программировать. В том числе учу разработчиков делать быструю оценку вычислительной сложности алгоритма. Зачем?!
На первый взгляд, это довольно академический навык, который не нужен за рамками экзамена по алгоритмам. Однако опытные разработчики используют его ежедневно, не задумываясь, на уровне рефлексов. Делают они это для грубого анализа кода, который читают, пишут или только собираются написать. Обычно быстрого анализа асимптотики достаточно, чтобы исключить случайное появление сильно неэффективного кода.
Сначала разберёмся, как делать оценку сложности, на примере короткой, но нетривиальной задачи. Потом я расскажу, как научится делать экспресс-оценку, и покажу статистику о том, как решали задачу-пример участники конференций Joker и DotNext.
Задача на Joker 2017 и DotNext 2017 Moscow
Коллеги, которые были прошлой осенью на конференциях Joker в Питере и DotNext в Москве, попросили меня придумать какую-нибудь задачку про сложность для стенда Контура.
Сначала я решил, что сложность — плохая тема, скучная. Но всё таки решил попробовать, и по-моему в результате получилось довольно красиво! Идея родилась легко, по пути домой, а дальше я почти час за клавиатурой пытался оформить её в короткий, но эффектный кусочек кода на C#. Вот что получилось:
Предлагалось, изучив этот код, ответить на три вопроса:
Наиболее точный ответ на последний вопрос предлагалось выбрать из внушительного списка вариантов:
Здесь самое время налить чашку кофе, прочитать фрагмент кода снова, порассуждать пять минут и выбрать ответ. Дальше будут спойлеры.
Решение
Но можно проявить чуть больше дотошности и вспомнить про неизменяемость строк в C# и Java. Действительно, конкатенация строк будет приводить к копированию, а значит работать будет за O(длина строки). А значит общая сложность будет чуть хуже логарифма. O(log²(x)) — наш выбор! Конечно, с практической точки зрения разница почти не заметна (см. эпиграф), но для задачки — самое то!
Получается, чтобы решить задачу, нужно довольно много:
Воу! Похоже, довольно круто получилось для такого маленького кусочка кода 🙂
Что вообще происходит?
Пора понять, что вообще делает этот странный код? Присмотритесь! Это же поиск списка простых чисел — методом недоделанного решета Эратосфена. Действительно, внутренний цикл удаляет каждое второе число, каждое третье и так далее. В итоге останутся только те, которые ни на что не делятся, кроме 1 и себя.
Тут не применены всем известные оптимизации (например, разумный выбор количества итераций циклов), а также добавлена пессимизация в виде ToBinaryString, чтобы совсем запутать. В итоге от исходной сложности O(n log(log(n))) и следа не осталось.
А вот некоторые интересные советы по оптимизации от участников конференций:
Участники Joker vs. участники DotNext
На Joker задачку решало 86 человек. Из них 8 дали верный ответ O(n log³(n)), а ещё 8 попались на уловку с конкатенацией и ответили O(n log²(n)).
На DotNext задачку решало 69 человек. Из них 10 ответили верно, а ещё 17 человек дали ответ O(n log²(n)). Но далеко идущих холиварных выводов о превосходстве дотнетчиков над джавистами по этой статистике сделать не получится. Мы точно знаем, что на DotNext приехали 49 контуровцев, и у них было преимущество.
Курс по оценке сложности за 2 часа
Вы ещё не забыли, что я учу программировать?
Прошлой осенью я запустил на ulearn.me, «нашей маленькой Курсере», миникурс по экспресс-оценке сложности алгоритмов. Его можно пройти всего за пару часов, он почти не содержит теории, зато придется решить 3 десятка задачек, ведущих вас от простых техник к более сложным. Если разбор этой задачи вам было понять сложновато — курс для вас.
Возможно, этот курс и повлиял на результаты. Тем более, что после Joker я добавил в него разбор элементов этой самой задачки — не пропадать же добру 🙂
Сложность алгоритмов. Big O. Основы.
Развитие технологий привело к тому, что память перестала быть критическим ресурсом. Поэтому когда говорят об анализе сложности алгоритма, обычно подразумевают то, насколько быстро он работает.
Но ведь время выполнения алгоритма зависит от того, на каком устройстве его запустить. Один и тот же алгоритм запущенный на разных устройствах выполняется за разное время.
Big O показывает верхнюю границу зависимости между входными параметрами функции и количеством операций, которые выполнит процессор.
Распространённые сложности алгоритмов
Здесь рассмотрены именно распространённые виды, так как рассмотреть все варианты врядли возможно. Всё зависит от алгоритма, который вы оцениваете. Всегда может появится какая-то дополнительная переменная (не константа), которую необходимо будет учесть в функции Big O.
Означает, что вычислительная сложность алгоритма не зависит от входных данных. Однако, это не значит, что алгоритм выполняется за одну операцию или требует очень мало времени. Это означает, что время не зависит от входных данных.
Пример № 1.
У нас есть массив из 5 чисел и нам надо получить первый элемент.
Насколько возрастет количество операций при увеличении размера входных параметров?
Нинасколько. Даже если массив будет состоять из 100, 1000 или 10 000 элементов нам всеравно потребуется одна операция.
Пример № 2.
Сложение двух чисел. Функция всегда выполняет константное количество операций.
Пример № 3.
Размер массива. Опять же, функция всегда выполняет константной количество операций.
Означает, что сложность алгоритма линейно растёт с увеличением входных данных. Другими словами, удвоение размера входных данных удвоит и необходимое время для выполнения алгоритма.
Такие алгоритмы легко узнать по наличию цикла по каждому элементу массива.
Пример № 3.
Означает, что сложность алгоритма растёт логарифмически с увеличением входных данных. Другими словами это такой алгоритм, где на каждой итерации берётся половина элементов.
К алгоритмам с такой сложностью относятся алгоритмы типа “Разделяй и Властвуй” (Divide and Conquer), например бинарный поиск.
Означает, что удвоение размера входных данных увеличит время выполнения чуть более, чем вдвое.
Примеры алгоритмов с такой сложностью: Сортировка слиянием или множеством n элементов.
Означает, что удвоение размера входных данных увеличивает время выполнения в 4 раза. Например, при увеличении данных в 10 раз, количество операций (и время выполнения) увеличится примерно в 100 раз. Если алгоритм имеет квадратичную сложность, то это повод пересмотреть необходимость использования данного алгоритма. Но иногда этого не избежать.
Такие алгоритмы легко узнать по вложенным циклам.
Пример № 1.
В функции есть цикл в цикле, каждый из них проходит массив длиной n, следовательно сложность будет: O(n * n) = O(n 2 )
Зачем изучать Big O
Шпаргалка
Небольшие подсказки, которые помогут определить сложность алгоритма.
Полезные ссылки
Оценка сложности и эффективности алгоритмов
У всех алгортимов есть 2 главные характеристики:
Их используют для того, чтобы сравнивать алгоритмы между собой. Одни алгоритмы работают быстрее, но требуют больше памяти, а другие наоборот.
Для большинства алгоритмов время выполнения и количество памяти нельзя выразить одним числом. Чем больше элементов будет во входящем массиве, тем дольше будут выполняться поиск и сортировка.
Для описания эффективности алгоритмов придумали нотацию Big-O.
Самый эффективный алгоритм в теории работает за постоянное время и расходует постоянное количество памяти. Как ни увеличивай объем входящих данных, сложность алгоритма не повысится. Эффективность (или сложность) такого алгоритма называют константным и записывают как O(1).
Пример алгоритма с постоянной сложностью:
Скорость выполнения и объем требуемой памяти этого алгоритма не зависит от длины входящего массива, поэтому сложность считается постоянной.
Сложность многих алгоритмов растет прямо пропорционально изменению количества входящих данных.
Если поиск в массиве из 10 элементов занимает 5 секунд, то в массиве из 100 элементов мы будем искать 100 секунд. В 10 раз дольше.
Такую сложность (эффективность) называют линейной и записывают как О(n).
Простые алгоритмы сортировки, такие как сортировка пузырьком или сортировка выбором имеют сложность О(n^2^).
Это не очень эффективно. При росте длины массива в 10 раз, время выполнения алгоритма увеличится в 10^2^ (в 100) раз!
Так происходит из-за того, что в алгоритме используется вложенный цикл. Сложность одного прохода мы оцениваем как O(n). Но проходим мы его не один раз, а **n **раз. Поэтому и получается сложность O(n * n) = O(n^2^).
В качестве примера можно представить двоичный поиск. На каждой итерации мы можем отбросить половину данных и работать только с оставшимися.