Как узнать площадь пятиугольника

Площадь правильного и неправильного пятиугольника: как рисовать, упражнения

Содержание:

В этом случае есть формула для вычисления точной площади правильного многоугольника, зная некоторые из его основных характеристик, которые мы выведем позже.

Если многоугольник не правильный, то есть имеет стороны разных размеров и неравные внутренние углы, единой формулы не существует.

Однако математики нашли методы вычислений, такие как разделение фигуры на другие с меньшим количеством сторон, такие как треугольники, квадраты и прямоугольники, размеры которых легко узнать или вычислить.

Как найти площадь правильного пятиугольника?

Мы собираемся взять правильный пятиугольник со стороной a и разделить его на 5 равных треугольников, как показано на рисунке, проведя отрезки от центра (красный) до вершин (синий).

В свою очередь, треугольники, как и тот, который выделен желтым справа на рисунке выше, делятся на два равных прямоугольных треугольника благодаря зеленому сегменту, который называется апофема.

Апофема определяется как перпендикулярный сегмент, который соединяет центр многоугольника с центром одной из сторон. Его длина L_К.

Площадь прямоугольного треугольника с основанием a / 2 и высотой L_К это:

Пентагон состоит из 10 таких треугольников, поэтому его площадь равна:

Но периметр п пятиугольника равно P =10а, поэтому площадь определяется как произведение периметра и длины апофемы:

Площадь правильного пятиугольника, знающая сторону a

Выражая длину апофемы L_К как функция стороны a, зная, что указанный угол составляет половину центрального угла, то есть 36º, что эквивалентно:

Методом элементарной тригонометрии через тангенс острого угла 36º:

загар (π / 5) = (a / 2) ÷ L_К

L_К= (а / 2) ÷ загар (π / 5)

Подставив в область, выведенную в предыдущем разделе, и зная, что P = 5a:

Площадь правильного пятиугольника, зная его радиус

cos 36º = cos (π / 5) = L_К ÷ R

sin 36º = sin (π / 5) = (a / 2) ÷ R

А = P x L_К / 2 = 5р. sin (π / 5) x R. cos (π / 5) = 5R 2 [sin (π / 5) x cos (π / 5)]

Используя формулу двойного угла:

грех (2θ) = 2 греха θ. cos θ

[sin (π / 5) x cos (π / 5)] = (1/2) sin 72º

Итак, подставив это значение, мы получим следующую формулу для площади правильного пятиугольника:

Как рассчитать площадь неправильного пятиугольника?

Триангуляция

Он состоит из деления фигуры на треугольники, площадь которых легче вычислить, или ее также можно проверить с другими фигурами, площадь которых известна, такими как квадраты, прямоугольники и трапеции.

Гауссовские детерминанты

Зная эти координаты, применяется гауссовский метод определителей для вычисления площади, которая определяется следующей формулой:

Полосы, сопровождающие формулу, представляют собой столбцы модуля или абсолютного значения.

Это означает, что даже если результат операции отрицательный, мы должны выразить его положительным знаком, а если он уже положительный, то его нужно оставить с этим знаком. Это потому, что площадь всегда является положительной величиной.

Процедура названа гауссовскими детерминантами в честь ее создателя, немецкого математика Карла Ф. Гаусса (1777-1855). Указанные операции эквивалентны определителю матрицы 2 × 2, например, первый определитель равен:

Чтобы найти площадь пятиугольника, мы должны решить 5 определителей, сложить результат алгебраически, разделить его на 2 и, наконец, выразить площадь всегда с положительным знаком.

Решенные упражнения

Упражнение 1

Решение

Поскольку это правильный пятиугольник, а у нас есть размеры стороны и апофемы, мы используем формулу, полученную выше:

Периметр P равен 5a = 5 x 5,9 см = 29,5 см.

A = 29,5 см x 4 см / 2 = 59 см 2

Упражнение 2.

Найдите площадь неправильного пятиугольника, как показано. Известны следующие размеры:

Решение

EA 2 + EC 2 = AB 2 + BC 2

Поскольку EA и AB измеряют одно и то же, отсюда следует, что:

Поскольку BC = 12, то ED = 12 / √2 = 8,485.

Используя эти значения, мы рассчитаем площадь каждого треугольника и добавим их в конце.

Площадь треугольника EDC

ED x DC / 2 = 8,485 2 / 2 = 36

Площадь треугольника AEC

EA x EC / 2 = EA x √2. ED / 2 = 5 x √2. 8 485/2 = 30

Площадь треугольника ABC

Тогда искомая область:

Это то же самое, что и треугольник AEC, поскольку они оба имеют одинаковые размеры.

Площадь неправильного пятиугольника

Наконец, запрашиваемая площадь представляет собой сумму площадей трех треугольников:

А = 36 + 30 + 30 единиц = 96 единиц.

Ссылки

40 лучших цитат Эдуарда Пансета о счастье и любви

Источник

Площадь многоугольника

Расчет площади многоугольника по введенным сторонами и диагоналям, разбивающим многоугольник на непересекающиеся треугольники

Пример многоугольника

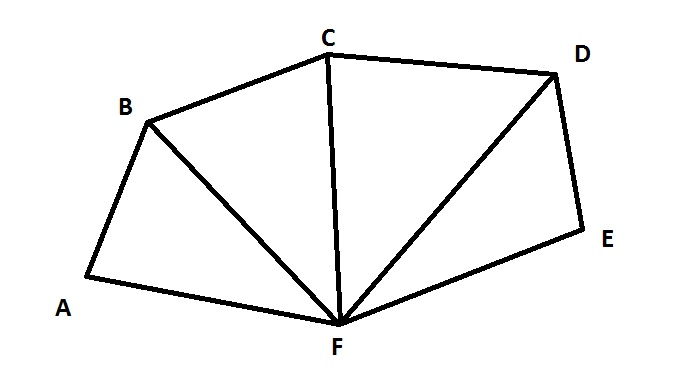
Данный калькулятор обсчитывает площадь многоугольника по введенным сторонами и диагоналям, разбивающим многоугольник на непересекающиеся треугольники.

Смотрим на картинку — площадь многоугольника ABCDE можно вычислить как сумму площадей треугольников ABD, BCD и ADE. Для этого, понятно, помимо длин сторон многоугольника, надо знать еще и длины диагоналей BD и AD, но это и все что нужно — площадь любого треугольника можно вычислить только по длинам его сторон, без измерения углов.

А это довольно удобно, например, при бытовом ремонте — длины-то всяко проще померять, чем углы.

Итак, измеряем длины сторон интересующего нас многоугольника, заносим их в таблицу, мысленно разбиваем многоугольник на треугольники, измеряем нужные диагонали, также заносим их в таблицу, после чего калькулятор рассчитывает площадь всей фигуры. Для проверки также выводятся площади обсчитанных им треугольников. В поле «Ошибка» выводится вершина, которую не удалось сопоставить ни одному треугольнику (если, например, введены еще не все диагонали).

По умолчанию в таблицу введены стороны и диагонали многоугольника на картинке, что легко исправить, нажав кнопку «Очистить таблицу».

Источник

Калькулятор площади пятиугольника

Пятиугольник представляет собой геометрическую фигуру с пятью углами. Существует множество разных пятиугольников, однако если стороны равны, а каждый угол фигуры равен 108 градусам, то многоугольник называется правильным и носит название «пентагон».

Геометрия пятиугольника

Пятиугольник — это фигура, которая состоит из пяти соединенных отрезков. Стороны произвольного многоугольника могут соединяться под разными углами, в результате чего фигура может быть невыпуклой. Наиболее ярким примером невыпуклого многоугольника является звезда, а пятиугольника — проекция зубчатой короны, когда два «зубца» выступают над прямоугольным основанием. Выпуклый многоугольник — это фигура, продолжение отрезков которого не пересекает других сторон. Если же мы продлим отрезки зубцов или лучей звезды, они пересекут другие стороны фигуры.

Пятиугольник в реальности

Невыпуклые геометрические фигуры редко встречаются в человеческой повседневности и обычно представляют собой основания для нестандартных призм. Наиболее распространенным пятиугольником в реальности считается пентагон — правильный многоугольник. Пентагон нашел применение в архитектуре и дизайне, и тезкой фигуры является одно из самых известных зданий Америки — штаб министерства обороны США.

Додекаэдр — платоново тело, каждая из 12 сторон которого является правильным пятиугольником. Додекаэдр используется в различных сферах, но наиболее известным представлением многогранника считается игральная кость d12, которая используется как генератор случайных чисел для настольных ролевых игр.

Несмотря на то, что многие организмы обладают пентасимметрией, например, морские звезды или плоды мушмулы, природные пятиугольные объекты практически не встречаются в природе.

Площадь пентагона

Площадь любой геометрической фигуры — это количественная оценка того, какую часть плоскости ограничивают ее стороны. Площадь правильного пятиугольника рассчитывается по общей для всех правильных многоугольников формуле:

S = n/4 × a 2 × ctg(pi/n),

где n – количество сторон фигуры, a – длина стороны.

Таким образом, если подставить n = 5 и выразить получившееся выражение десятичной дробью, мы получим простую формулу для вычисления площади пентагона:

где a — длина одной стороны.

Сторона пентагона и радиусы вписанной r и описанной окружности R приблизительно соотносятся как:

Программный код калькулятора использует эти соотношения, что позволяет вам найти площадь правильного пятиугольника, зная только один параметр из перечисленных:

Рассмотрим на примерах, как вычислить площадь правильного пятиугольника.

Примеры из жизни

Пентагон

Штаб министерства обороны США — это всемирно известное здание, которое имеет форму правильного пятиугольника. Каждая сторона штаба имеет длину 281 м и мы без проблем можем узнать, какую площадь занимает здание. Для более удобного представления выразим длину в километрах, введем эти данные в форму калькулятора a = 0,281 и получим результат:

Площадь Пентагона составит 0,136 квадратных километров.

Школьная задача

К примеру, необходимо вычислить площадь пентагона, зная, что радиус вписанной окружности составляет 15 см. Мы можем выразить сторону многоугольника через простое соотношение радиуса вписанной окружности и длины стороны a = 1,4131 r, после чего посчитать по формуле его площадь. Проще всего ввести значение радиуса в ячейку «Радиус вписанной окружности r» и получить мгновенный результат:

Кроме непосредственно площади фигуры, калькулятор автоматически подсчитал остальные атрибуты пятиугольника.

Заключение

Пентагон нечасто встречается в реальной жизни, однако при решении производственных вопросов или школьных задач вам может понадобиться рассчитать площадь или периметр правильных многоугольников. Наш каталог калькуляторов к вашим услугам.

Источник

Пятиугольник, виды, свойства и формулы

Пятиугольник, виды, свойства и формулы.

Пятиугольник – это многоугольник, общее количество углов (вершин) которого равно пяти.

Пятиугольник, выпуклый и невыпуклый пятиугольник:

Пятиугольник – это многоугольник, общее количество углов (вершин) которого равно пяти.

Пятиугольник – фигура, состоящая из пяти углов (вершин), которые образуются пятью отрезками (сторонами).

Пятиугольник может быть выпуклым и невыпуклым.

Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.

Соответственно выпуклый пятиугольник – это пятиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Рис. 1. Выпуклый пятиугольник

Сумма внутренних углов любого выпуклого шестиугольника равна 540°.

Невыпуклый пятиугольник – это пятиугольник, у которого одна часть его точек лежат по одну сторону, а другая часть – по другую от любой прямой, проходящей через две его соседние вершины.

Рис. 2. Невыпуклый пятиугольник

Звёздчатый пятиугольник (пентаграмма) – пятиугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного семиугольника многоугольника. Стороны звёздчатого пятиугольника могут пересекаться между собой.

Правильный многоугольник:

Правильный пятиугольник (пентагон) – это правильный многоугольник с пятью сторонами.

В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.

Правильный пятиугольник – это пятиугольник, у которого все стороны равны, а все внутренние углы равны 108°.

Рис. 3. Правильный пятиугольник

Правильный пятиугольник имеет 5 сторон, 5 углов и 5 вершин.

Правильный пятиугольник может быть построен с помощью циркуля и линейки или вписыванием его в заданную окружность, или построением на основе заданной стороны.

Свойства правильного пятиугольника:

1. Все стороны правильного пятиугольника равны между собой.

2. Все углы равны между собой и каждый угол равен 108°.

Рис. 4. Правильный пятиугольник

3. Сумма внутренних углов правильного пятиугольника равна 540°.

4. Все биссектрисы углов между сторонами равны и проходят через центр правильного пятиугольника O.

Рис. 5. Правильный пятиугольник

5. Количество диагоналей правильного пятиугольника равно 5.

Рис. 6. Правильный пятиугольник

6. Центр вписанной окружности O₁ совпадает с центром описанной окружности O₂, что и образуют центр пятиугольника O.

Рис. 7. Правильный пятиугольник

7. Диагонали правильного пятиугольника являются трисектрисами его внутренних углов.

Рис. 8. Правильный пятиугольник

8. Отношение диагонали правильного пятиугольника к стороне равно золотому сечению.

Рис. 9. Правильный пятиугольник

Построение правильного пятиугольника:

Метод построения правильного пятиугольника вписыванием его в заданную окружность:

1. Постройте окружность, в которую будет вписан пятиугольник, и обозначьте её центр как O.

2. Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.

3. Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.

4. Постройте точку C посередине между O и B.

5. Проведите окружность с центром в точке C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.

6. Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.

7. Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.

8. Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.

9. Постройте правильный пятиугольник AEGHF.

Формулы правильного пятиугольника:

Пусть a – сторона пятиугольника, r – радиус окружности, вписанной в пятиугольник, R – радиус описанной окружности пятиугольника, S – площадь пятиугольника, h – высота пятиугольника, d – диагональ пятиугольника, Ф – отношение золотого сечения.

Формулы площади правильного пятиугольника:

Формулы высоты правильного пятиугольника:

Формулы стороны правильного пятиугольника:

Формулы диагонали правильного пятиугольника:

Формулы радиуса окружности, вписанной в правильный пятиугольник:

Формулы радиуса окружности, описанной вокруг правильного пятиугольника:

Правильный пятиугольник в природе, технике и культуре:

Пентасимметрию можно наблюдать в некоторых фруктах (например, у мушмулы германской), у иглокожих (например, у морских звёзд) и у некоторых растений.

Исследования формирования водяного льда на ровной поверхности меди при температурах 100-140 K показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры.

Пентагон — здание Министерства обороны США — имеет форму правильного пятиугольника.

Паркет, тротуарная плитка, мозайки и т.п. может выкладываться элементами, которые имеют вид пятиугольников.

Государственный знак качества СССР имеет форму пятиугольника с выпуклыми сторонами.

Источник

Как рассчитать площадь пятиугольника?

Площадь правильного пятиугольника рассчитывается по общей для всех правильных многоугольников формуле: S = n/4 × a2 × ctg(pi/n), где n – количество сторон фигуры, a – длина стороны.

Как вычислить площадь многоугольника по периметру?

Формула для нахождения площади правильного многоугольника: Площадь = 1/2 х периметр х апофема.

Как правильно посчитать площадь?

Простая комната прямоугольной или квадратной формы

В помещении, которое представляет собой прямоугольник или квадрат, нужно измерить длину и ширину и умножить значения между собой. Вы получите площадь комнаты в квадратных метрах. Формула по которой можно высчитать площадь: S комнаты = А х B, где A – длина, B – ширина.

Как найти площадь шестиугольника?

Как найти площадь шестиугольника при известной длине стороны Запишите формулу. Так как правильный шестиугольник состоит из 6 равносторонних треугольников, то формула образована из формулы нахождения площади равностороннего треугольника: Площадь = (3√3 s2)/ 2 где s — длина стороны правильного шестиугольника.

Как найти площадь пятиугольника вписанного в окружность?

То есть площадь многоугольника, в который вписана окружность известного радиуса, равна произведению этого радиуса на полупериметр многоугольника.

Как найти площадь неправильного многоугольника?

Для нахождения площади какого-нибудь неправильного многоугольника нужно его разбить на треугольники, вычислить площадь каждого треугольника в отдельности и результаты сложить.

Как найти площадь неправильного многоугольника по периметру?

Периметр такого многоугольника равен произведению длины стороны a на общее их количество n. Формула площади правильного многоугольника, зная стороны, представляет собой произведение количества и квадрата длины, деленное на четыре тангенса угла, полученного делением 180 градусов на то же количество.

Как считается 1 квадратный метр?

Умножьте длину на ширину.

Как только переведете все измерения в метры, умножьте длину на ширину и получите площадь измеряемого объекта. При необходимости воспользуйтесь калькулятором. Например: 2.35м x 1.08м = 2.538 квадратных метра (m2).

Как рассчитать квадратный метр стены?

Для начала необходимо измерить высоту и ширину всех стен, после чего воспользоваться достаточно простой математической формулой «S=H×L», где H — это высота стены, L — её длина, ну а S – соответственно необходимая нам площадь.

Как считать квадратные метры пола?

Посчитать квадратные метры можно по формуле:S. = H*B, где S – искомая площадь, единица измерения метр квадратный;H – длина помещения, м;B – его ширина;В случае с квадратной комнатой достаточно длину ее стороны возвести в квадрат, так как длина каждой стены в этом случае будет одинаковой.

Как найти площадь правильного шестиугольника?

Главная особенность шестиугольника заключается в том, что длина радиуса описанной окружности совпадает с длиной стороны многоугольника. Благодаря этому свойству можно легко найти площадь гексагона по формуле: S = 2,59 R2 = 2,59 a2.

Как найти периметр шестиугольника формула?

Чтобы найти периметр шестиугольника, измерьте и сложите длины всех его шести сторон. Р = а1+а2+а3+а4+а5+а6,где P – периметр шестиугольника, а а1, а2 … а6 – длины его сторон. Единицы измерения каждой из сторон приведите к одному виду – в этом случае достаточно будет сложить только числовые значения длин сторон.

Как найти радиус правильного шестиугольника?

Формулы для правильного шестиугольника

Как найти площадь описанной фигуры?

S = (a * b * с) : 4 * R, где a, b и с — стороны треугольника, а R — радиус описанной окружности.

Как найти площадь пятиугольника 4 класс?

В этом случае для вычисления площади пятиугольника используйте следующую формулу: A = (5/2)r2sin72˚, где r — радиус описанной окружности.

Что такое описанный многоугольник?

Вписанным в круг многоугольником называется такой многоугольник, вершины которого лежат на окружности. Описанным около круга многоугольником называется такой многоугольник, стороны которого касаются окружности. Описанной около многоугольника окружностью называется окружность, проходящая через его вершины.

Источник