Как узнать периметр шестиугольника
Формулы для расчета периметра шестиугольника
Иногда возникает необычная для учащегося задача по нахождению периметра шестиугольника. Не всегда на этот вопрос можно ответить сразу. В этой статье мы рассмотрим подробным образом, как найти периметр шестиугольника согласно формулам, а также вычислить и находить его другими способами.
Описание фигуры
Непосредственно шестиугольник представляет собой плоскую фигуру, состоящую из шести отрезков, с расположением под углом 120 градусов относительно друг друга. Имеет научное название гексагон. Вокруг него или внутри можно вписать либо описать окружность. Между собой радиус и сторона многоугольника соотносятся по следующим формулам:
Гексагон является очень популярной фигурой, ее имеют гайки, карандаши, соты, снежинки и многое другое. Является оптимальным вариантом для того, чтобы без пробелов замостить все пространство. Одним из примеров этого является Мостовая гигантов, образовавшаяся в результате соединения более чем 40 тысяч базальтовых колонн в результате извержения древнего вулкана и элегантно замостившая поверхность побережья в Северной Ирландии.
Поиски вышеописанного параметра гексагона являются простой, но в то же время довольно интересной задачей. Найдя периметр, можно убедиться в правильности замощенного пространства и отсутствии пробелов при составлении будущей документации.
До начала вычислений
Всем известно, что периметр плоской фигуры, к которой относится шестиугольник, является ничем иным, как длиной ограничивающей линии. Для нахождения периметра такой фигуры как гексагон, достаточно будет найти и сложить длины всех его сторон. Чтобы произвести эту процедуру, нужно измерить длины всех составляющих его отрезков. Значительно облегчается задача, если данная фигура имеет правильную форму. Разберем далее, как нужно искать периметр шестиугольника.
Первый вариант
Инструментарий достаточно простой. Понадобятся всего лишь циркуль и линейка. Вычислять периметр гексагона нужно следующим образом: измерить линейкой длину каждой из 6 сторон и сложить полученные значения. Все измерения длин сторон должны иметь единую систему единиц, тогда достаточно будет сложить числовые значения. То есть, единица измерения параметра шестиугольника совпадет с аналогичными параметрами длин отрезков.
Например, имеются следующие отрезки: 2 сантиметра, 5,4,3,2 и 1 миллиметр. В этом случае нужно перевести 2 сантиметра в миллиметры из расчета 1 сантиметр равняется 10 миллиметрам и суммируете P=20+5+4+3+2+1=35 миллиметров. Таким образом рассчитывается периметр большинства видов шестиугольников.
Правильный шестиугольник
В случае, если шестиугольник имеет правильную форму, то расчет нужного параметра становится гораздо проще.
Например, известен прямоугольник, вписанный в окружность, имеющую диаметр 20 сантиметров. Тогда радиус будет в два раза меньше и составит 10 сантиметров. Полученную величину умножаем на 6 сторон и получаем периметр.
Иные варианты расчета
Если известен радиус вписанной в многоугольник окружности, рекомендуется использовать формулу P=4sqrt (3)*r, в которой r является радиусом вписанной окружности.
Другие способы измерения периметра шестиугольника можно найти в специализированной литературе и на особых порталах.
Шестиугольник относят к очень эффективной фигуре. Она встречается как в реальности, так и среди природных явлений. Если же вы боитесь, что не сможете правильно сами посчитать заданную величину, на помощь придут специальные онлайн-калькуляторы, в которых можно ввести необходимые данные для вычисления периметра. Удачной математической работы с поисками периметра для гексагона.
Видео
Посмотрите, как рассчитывается площадь правильного шестиугольника.
Калькулятор периметра шестиугольника
Правильный шестиугольник или гексагон — это многоугольник с шестью равными углами и шестью равными сторонами. Это правильная фигура, которая широко встречается как в природе, так и в человеческой повседневности.
Геометрия шестиугольника
Шестиугольник — фигура на плоскости, ограниченная шестью равными отрезками, которые пересекаются под углом 120 градусов. Изучением многоугольников в целом и гексагона в частности занимался отец геометрии Евклид, который в «Началах» предложил способ построения правильного шестиугольника при помощи циркуля и линейки.
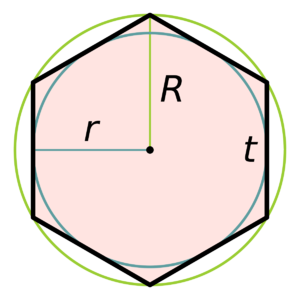
Вокруг любой правильной геометрической фигуры можно описать окружность или вписать ее внутрь. Гексагон не исключение. Сторона фигуры a и радиусы описанной окружности R и вписанной r соотносятся как:
Главная особенность гексагона состоит в том, что сторона многоугольника и радиус описанной окружности абсолютно равны, так как 2sin(pi/6) = 1.
Примеры шестиугольников
Гексагон — довольно распространенная геометрическая фигура. В человеческой повседневности форму шестиугольника принимают грани таких объектов как гайки, карандаши или детали машин. В природе шестиугольную форму имеют пчелиные соты, снежинки, а также кристаллические решетки некоторых соединений углерода. Кроме того, существует уникальное космическое явление на Сатурне — гигантский гексагон, который представляет собой атмосферный вихрь в виде правильного шестиугольника.
Шестиугольник — эффективная фигура, позволяющая замостить поверхность без пробелов или наложений. Кафель или тротуарная плитка часто принимают форму гексагона, однако наиболее выдающимся примером замощения поверхности шестиугольником является Мостовая гиганта — памятник природы, образованный соединением более 40 000 базальтовых колонн. Шестиугольные колонны Мостовой гиганта образовались в результате древнего извержения вулкана и элегантно замостили поверхность североирландского побережья.
Периметр гексагона
Периметр плоской фигуры — это числовая характеристика, показывающая сумму длин всех его сторон. Гексагон — правильная геометрическая фигура, следовательно, все ее стороны равны. Формула для вычисления периметра шестиугольника предельно проста:
Кроме того, благодаря замечательному свойству шестиугольника, периметр можно вычислить, зная радиус описанной окружности:
Наш калькулятор также использует зависимость между стороной гексагона и радиусом вписанной окружности, поэтому вы можете рассчитать периметр геометрической фигуры, зная только одну из трех переменных на выбор. Кроме того, калькулятор автоматически рассчитает не только периметр, но и остальные атрибуты шестиугольника. Рассмотрим пару примеров.
Примеры из реальной жизни
Снежинка
Снежинка представляет собой снежный или ледяной кристалл в форме правильной шестиугольной пластинки. Естественно, снежинка — слишком мала для того, чтобы мы могли измерить ее натуральный размер и посчитать периметр на онлайн-калькуляторе. Однако включим воображение и представим, что одна сторона снежинки имеет длину, равную 12 условных единиц. Для подсчета периметра такого кристалла нам понадобится просто умножить длину стороны на 6 или ввести значение в форму калькулятора «Сторона». Мы получим ответ:
Также мы узнали, что в нашу воображаемую снежинку мы можем вписать окружность с радиусом r = 10,39.
Школьная задача
В задаче по геометрии требуется найти периметр правильного шестиугольника, зная, что радиус вписанной в него окружности составляет 15 см. Мы знаем, что радиус окружности и сторона гексагона соотносятся как r = 0,866 a и можем вручную подсчитать сначала длину стороны, а затем периметр плоской фигуры. Мы можем сэкономить время и просто указать значение радиуса в ячейке калькулятора «Радиус вписанной окружности r» и получить мгновенный результат:
Заключение
Шестиугольник — эффективная фигура, которая встречается как в природе, так и в человеческой повседневности. Используйте наш онлайн-калькулятор для расчета периметра правильных шестиугольников.
Как найти периметр шестиугольника?
Периметр шестиугольника так же вычисляется как и периметр треугольника, четырехугольника. Периметр- это сумма длин всех сторон геометрической фигуры. Измеряйте длину каждой стороны вашего шестиугольника, запишите данные и сложите их.
Чтобы найти периметр многоугольника, нужно сложить длины его сторон.
Чтобы найти периметр шестиугольника, помню еще с уроков математики, надо знать длину каждой его стороны.
Или просто измерить каждую его сторону.
А затем надо сложить все полученные измерения и мы получим периметр.
Периметр правильного шестиугольника равен трём его центральным хордам, соединяющим противоположные вершины(или трём диаметрам описывающей шестигранник окружности).Если этот шестигранник неправильный и находится на пересеченной местности, то можно пройтись по его сторонам с шагомером.
Шестиугольники могут быть разными: выпуклыми, с прямолинейными сторонами или с криволинейными, правильными у которого все стороны равны или неправильными. Периметр любого многоугольника равен сумме длин всех его сторон. Определенный ответ можно дать только о периметре правильного выпуклого прямолинейного шестиугольника вписанного в окружность с радиусом равным 1. Периметр такого шестиугольника равен 6-ти радиусам.
Вопрос о соотношении площади и периметра у меня всегда вызывает некоторое недоумение: ведь эти величины не находятся в некоторой прямой зависимости и одна и та же площадь может быть получена при большом многообразии периметра сторон, ее огораживающих.
Так, например, те же самые 75 соток площади из вопроса будут соответствовать 7 с половиной тысячам квадратных метров, а вот периметр указанного участка (сотка все-таки ассоциируется с землей) может быть:
ну а участок 1 на 7500 метров будет иметь периметр 15002 метра.
А вот площадь участка от формы не зависит. Вот с площади и начнём.
Одна сотка имеет площадь 100 квадратных метров. Стало быть 85 соток имеют площадь 8500 квадратных метров. Для простоты это можно представить в виде прямоугольника 100метров х 85 метров Тогда периметр этого прямоугольника 370 метров.
Как найти периметр шестиугольника с разными сторонами?
Чтобы найти периметр шестиугольника, измерьте и сложите длины всех его шести сторон. Р = а1+а2+а3+а4+а5+а6,где P – периметр шестиугольника, а а1, а2 … а6 – длины его сторон.
Как найти периметр многоугольника с разными сторонами?
Перемножьте значение стороны на количество сторон, чтобы вычислить периметр. Формула для нахождения периметра правильного многоугольника: периметр = количество сторон x длину любой стороны. В нашем примере значение стороны квадрата 6 см и у квадрата 4 стороны. Поэтому 6 х 4 = 24 см — это периметр квадрата.
Как найти периметр шестиугольника если известен радиус?
Если вам известен радиус описанной окружности, то достаточно воспользоваться формулой в виде P=R*6, где R — радиус описанной окружности.
Как найти площадь шестиугольника зная периметр?
Формула площади: S = 1/2*p*m, где p – периметр, m – апофема. Найдём через апофему периметр шестиугольника.
Как найти периметр фигуры с разными сторонами?
периметр равностороннего многоугольника равен длине одной его стороны умноженной на количество сторон. Ну а если известен периметр равностороннего многоугольника, то вычислить длины его сторон очень просто, надо разделить его периметр на количество сторон.
Как найти периметр прямоугольника с разными сторонами?
Как найти периметр многоугольника в окружности?
Периметр — это сумма сторон фигуры. Так как у правильного полигона все стороны равны, то формула для вычисления периметра фигуры предельно проста: P = a × n, где a — длина стороны, n — количество сторон.
…
Периметр многоугольника
Как найти периметр правильного шестиугольника?
Чтобы найти периметр шестиугольника, измерьте и сложите длины всех его шести сторон. Р = а1+а2+а3+а4+а5+а6,где P – периметр шестиугольника, а а1, а2 … а6 – длины его сторон. Единицы измерения каждой из сторон приведите к одному виду – в этом случае достаточно будет сложить только числовые значения длин сторон.
Как найти радиус правильного шестиугольника?
По свойству правильного шестиугольника радиус r вписанной окружности равен перпендикуляру, проведенному из центра правильного шестиугольника (центр вписанной и описанной окружности) к стороне шестиугольника; причем этот перпендикуляр падает в середину стороны.
Как найти сторону шестиугольника через радиус?
При известном радиусе r окружности вписанной в правильный шестиугольник сторона a вычисляется как отношение двух радиусов вписанной в правильный шестиугольник окружности и корня из числа 3.
Как посчитать квадратуру шестиугольника?
Площадь правильного шестиугольника равна площади равностороннего треугольника умноженной на шесть.
Как найти площадь шестиугольника зная длину окружности?
Формула для нахождения площади правильного шестиугольника через радиус вписанной окружности: S = 2 3 ⋅ r 2
Как найти площадь неправильного шестиугольника?
треугольника: S = (3√3)/4 * R2; квадрата: S = 2 * R2; шестиугольника: S = (3√3)/2 * R2.
Как найти периметр неправильной фигуры?
Периметр прямоугольника — сумма длины и ширины, умноженная на два. Формула параллелограмма выглядит соответственно. P = 2 * (a + b), где a — ширина, b — высота.
Как найти периметр квадрата с разными сторонами?
Формула для вычисления периметра квадрата: P = 4s, где s – длина стороны квадрата. Определите длину одной стороны квадрата и умножьте ее на 4, чтобы найти периметр. Чтобы определить длину стороны, измерьте ее линейкой или посмотрите ее значение в учебнике (задаче).
Периметр правильного шестиугольника и формула онлайн
Кредиты
Периметр гексагона
Периметр плоской фигуры — это числовая характеристика, показывающая сумму длин всех его сторон. Гексагон — правильная геометрическая фигура, следовательно, все ее стороны равны. Формула для вычисления периметра шестиугольника предельно проста:
Кроме того, благодаря замечательному свойству шестиугольника, периметр можно вычислить, зная радиус описанной окружности:
Наш калькулятор также использует зависимость между стороной гексагона и радиусом вписанной окружности, поэтому вы можете рассчитать периметр геометрической фигуры, зная только одну из трех переменных на выбор. Кроме того, калькулятор автоматически рассчитает не только периметр, но и остальные атрибуты шестиугольника. Рассмотрим пару примеров.
Правильный шестиугольник
В случае, если шестиугольник имеет правильную форму, то расчет нужного параметра становится гораздо проще.
Например, известен прямоугольник, вписанный в окружность, имеющую диаметр 20 сантиметров. Тогда радиус будет в два раза меньше и составит 10 сантиметров. Полученную величину умножаем на 6 сторон и получаем периметр.
Как найти периметр многоугольника в окружности?
Периметр — это сумма сторон фигуры. Так как у правильного полигона все стороны равны, то формула для вычисления периметра фигуры предельно проста: P = a × n, где a — длина стороны, n — количество сторон.…Периметр многоугольника
Как найти периметр прямоугольника с разными сторонами?
До начала вычислений
Всем известно, что периметр плоской фигуры, к которой относится шестиугольник, является ничем иным, как длиной ограничивающей линии. Для нахождения периметра такой фигуры как гексагон, достаточно будет найти и сложить длины всех его сторон. Чтобы произвести эту процедуру, нужно измерить длины всех составляющих его отрезков. Значительно облегчается задача, если данная фигура имеет правильную форму. Разберем далее, как нужно искать периметр шестиугольника.
Что такое шестиугольник?
Правильный шестиугольник определяется как шестиугольник, который одновременно является равносторонним и равноугольным. Он бицентрический, что означает, что он является как циклическим (имеет описанную окружность), так и касательным (имеет вписанную окружность). Общая длина сторон равна радиусу описанной окружности или описанной окружности, который равен 2 / sqrt (3), умноженным на апофему (радиус вписанной окружности). Все внутренние углы составляют 120 градусов. Правильный шестиугольник имеет шесть симметрий вращения.