Как узнать основание параллелограмма
Основание параллелограмма
Основание параллелограмма — это сторона, к которой можно
провести перпендикуляр из точки, лежащей на противоположной стороне.
У каждого параллелограмма только два основания. От любой
точки, лежащей на основании параллелограмма, можно провести
перпендикуляр только к одной точке на противоположной стороне.
Так, как у параллелограмма два основания, соответственно
перпендикуляры, которые проведены из любого основания,
оканчиваются на противоположном основании.
В параллелограмме все перпендикуляры,
имеют начало и конец на двух основаниях.
Площадь параллелограмма рассчитывается через
основание параллелограмма (a) и его высоту (h):
Основания у параллелограмма параллельны
друг другу и не имеют общих точек.
Если отрезок можно провести из вершины параллелограмма
к его основанию, под углом 90 градусов, то этот отрезок разделит
параллелограмм на две геометрические фигуры — треугольник
и прямоугольную трапецию. Два отрезка уже разделят параллелограмм
на два треугольника и прямоугольник между ними.
Каждое основание параллелограмма имеет две общие точки с
двумя сторонами, которые не являются основаниями.
Как найти основание параллелограмма? Основание легко
найти, зная формулу площади параллелограмма. Исходя из
этой формулы, формула основания следующая:
a — основание
S — площадь
h — высота
Углы, которые прилежат к любому из оснований,
составляют в сумме 180 градусов.
Параллелограмм. Формулы, признаки и свойства параллелограмма
 |  |
| Рис.1 | Рис.2 |
Признаки параллелограмма
AB||CD, AB = CD (или BC||AD, BC = AD)
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°
AC 2 + BD 2 = AB 2 + BC 2 + CD 2 + AD 2
Основные свойства параллелограмма
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°
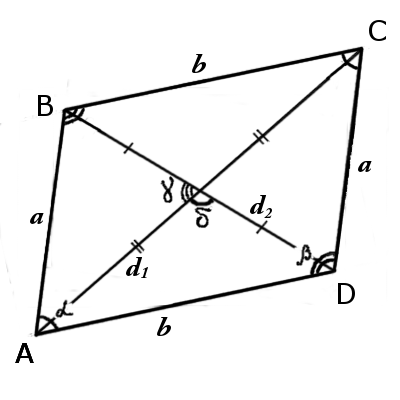
8. Диагонали параллелограмма пересекаются и точкой пересечения делят друг друга пополам:
| AO = CO = | d 1 |
| 2 | |
| BO = DO = | d 2 |
| 2 |
AC 2 + BD 2 = 2AB 2 + 2BC 2
Стороны параллелограмма
Формулы определения длин сторон параллелограмма:
1. Формула сторон параллелограмма через диагонали и угол между ними:
2. Формула сторон параллелограмма через диагонали и другую сторону:
3. Формула сторон параллелограмма через высоту и синус угла:
| a = | h b |
| sin α |
| b = | h a |
| sin α |
4. Формула сторон параллелограмма через площадь и высоту:
| a = | S |
| ha |
| b = | S |
| hb |
Диагонали параллелограмма
Формулы определения длины диагонали параллелограмма:
d 2 = √ a 2 + b 2 + 2 ab·cosβ
d 1 = √ a 2 + b 2 + 2 ab·cosα
4. Формула диагонали параллелограмма через площадь, известную диагональ и угол между диагоналями:
| d 1 = | 2S | = | 2S |
| d 2· sinγ | d 2· sinδ |
| d 2 = | 2S | = | 2S |
| d 1· sinγ | d 1· sinδ |
Периметр параллелограмма
Формулы определения длины периметра параллелограмма:
P = 2 a + 2 b = 2( a + b )
3. Формула периметра параллелограмма через одну сторону, высоту и синус угла:
| P = | 2( b + | h b | ) |
| sin α |
| P = | 2( a + | h a | ) |
| sin α |
Площадь параллелограмма
Формулы определения площади параллелограмма:
3. Формула площади параллелограмма через две диагонали и синус угла между ними:
| S = | 1 | d 1 d 2 sin γ |
| 2 |
| S = | 1 | d 1 d 2 sin δ |
| 2 |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Параллелограмм
Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны. Площадь параллелограмма равна произведению его основания (a) на высоту (h). Также можно найте его площадь через две стороны и угол и через диагонали.
Разновидностями параллелограмма (частные случаи) являются квадрат, прямоугольник и ромб.
Свойства параллелограмма
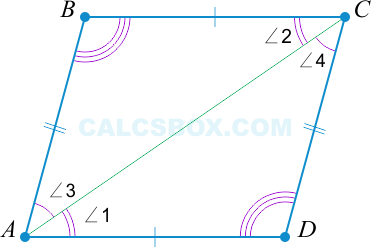
1. Противоположные стороны тождественны
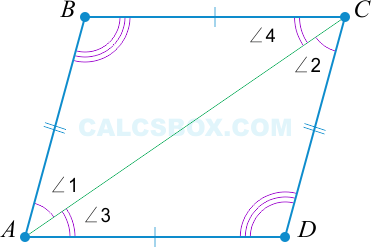
Так как \( ABCD \) — параллелограмм, то справедливо следующее:
\( AD || BC \Rightarrow \angle 1 = \angle 2 \) как лежащие накрест.
\( AB || CD \Rightarrow \angle3 = \angle 4 \) как лежащие накрест.
Следовательно, \( \triangle ABC = \triangle ADC \) (по второму признаку: \( \angle 1 = \angle 2, \angle 3 = \angle 4 \) и \( AC \) — общая).
2. Противоположные углы тождественны
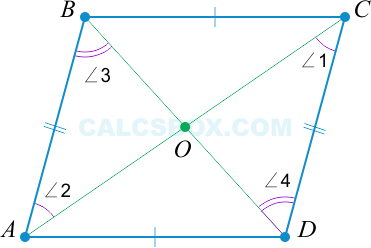
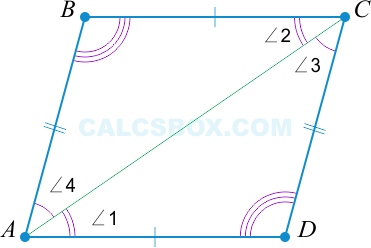
3. Диагонали разделены пополам точкой пересечения
Таким образом видно, что \( \triangle AOB = \triangle COD \) по второму признаку равенства треугольников (два угла и сторона между ними). То есть, \( BO = OD \) (напротив углов \( \angle 2 \) и \( \angle 1 \) ) и \( AO = OC \) (напротив углов \( \angle 3 \) и \( \angle 4 \) соответственно).
Признаки параллелограмма
Если лишь один признак в вашей задаче присутствует, то фигура является параллелограммом и можно использовать, все свойства данной фигуры.
Для лучшего запоминания, заметим, что признак параллелограмма будет отвечать на следующий вопрос — «как узнать?». То есть, как узнать, что заданная фигура это параллелограмм.
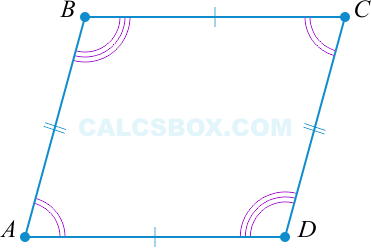
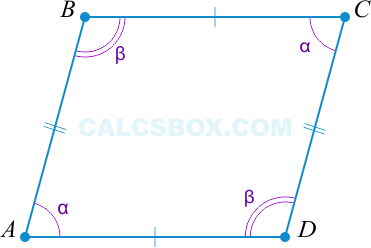
1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны
\( AB = CD \) ; \( AB || CD \Rightarrow ABCD \) — параллелограмм.
Первый признак верен.
2. Параллелограммом является такой четырехугольник, у которого противоположные стороны равны
Второй признак верен.
3. Параллелограммом является такой четырехугольник, у которого противоположные углы равны
Третий признак верен.
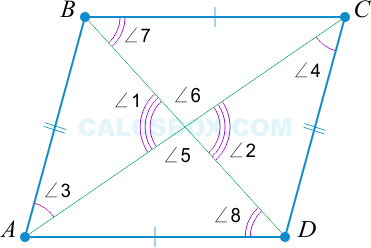
4. Параллелограммом является такой четырехугольник, у которого диагонали разделены точкой пересечения пополам
\( AO = OC \) ; \( BO = OD \Rightarrow \) параллелограмм.
Стороны и высота параллелограмма
Свойства
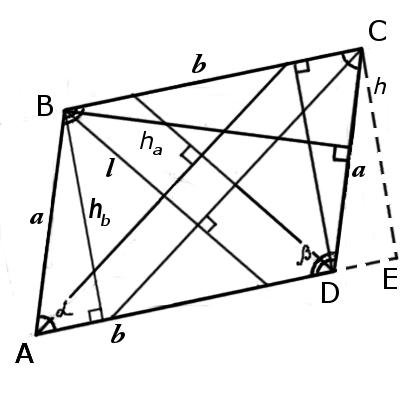
В параллелограмме противоположные стороны друг другу параллельны, а прилежащие находятся образуют определенный угол, поэтому чтобы определить большинство параметров параллелограмма нужно знать кроме сторон высоту или угол, их соединяющий. Если заданы стороны и высота, то одними из первых можно рассчитать периметр и площадь параллелограмма. Периметр параллелограмма, зная стороны, выглядит как их удвоенная сумма, а площадь является произведением высоты и стороны, на которую она опущена. P=2(a+b) S=ah_a=bh_b
Чтобы иметь возможность продолжать расчеты, необходимо найти углы между сторонами α и β. Используя прямоугольный треугольник, образованный высотой со стороной параллелограмма, выводим их взаимосвязь в тригонометрическое отношение. Затем, зная один из углов, в зависимости от того, какая высота была дана, отнимаем его из 180 градусов, чтобы найти второй. (рис.106.1) sinα=h_b/a sinβ=h_a/b α=180°-β β=180°-α
Зная углы и стороны, можно найти диагонали параллелограмма по теореме косинусов в треугольниках, которые они образуют со сторонами. Каждая диагональ будет равна корню из суммы квадратов сторон параллелограмма и разности удвоенного их произведения на косинус угла между ними. (рис.106.2) d_1=√(a^2+b^2-2ab cosβ ) d_2=√(a^2+b^2-2ab cosα )
Используя эту же теорему косинусов, можно найти угол между диагоналями в одном из четырех треугольников, образованных ими, где сторонами являются половины диагоналей и одна из сторон параллелограмма. (рис.106.3) cosγ=(〖d_1/4〗^2+〖d_2/4〗^2-a^2)/((d_1 d_2)/4)=(〖d_1〗^2+〖d_2〗^2-4a^2)/(2d_1 d_2 ) cosδ=(〖d_1〗^2+〖d_2〗^2-4b^2)/(2d_1 d_2 )
Биссектрисы параллелограмма, проведенные из углов α и β, образуют равнобедренные треугольники, в которых сама биссектриса является основанием, а боковыми конгруэнтными сторонами становится меньшая сторона параллелограмма. Треугольник считается равнобедренным, так как из свойств биссектрисы и суммы углов в треугольнике следует, что углы при основании такого треугольника конгруэнтны. Используя теорему косинусов, можно найти биссектрисы параллелограмма через стороны. (рис. 106.4) l_α=√(2a^2-2a^2 cosβ )=a√(2-2 cosβ ) l_β= b√(2-2 cosα )