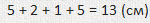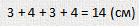Как узнать длину ломаной
Учебник. Моро 2 класс 1 часть. Страница 32
Длина ломаной
Узнаем, как можно найти длину ломаной разными способами.
Будем учиться находить и сравнивать длины ломаных.
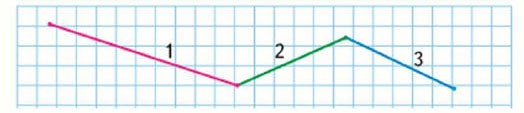
1. Длину ломаной можно узнать двумя способами.
1) Узнать длину каждого звена ломаной и найти сумму этих длин можно так: 5 + 3 + 3=11 (см).
А можно так:
2) Начертить прямую. С помощью циркуля отложить на прямой один за другим отрезки, равные по длине звеньям ломаной, и узнать длину всего получившегося отрезка (11 см).
Сравни эти два способа: сколько измерений сделали в первом случае? во втором?
В первом случае я сделал три измерения — измерил 3 звена ломаной. Во втором случае я измерял только 1 раз — получившейся на прямой отрезок.
Сделай вывод.
Для меня удобнее первый способ потому, что во втором случае надо ещё чертить прямую и работать с циркулем. А в первом случае достаточно только измерить звенья линейкой и сложить получившиеся длины.
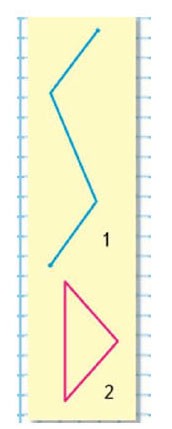
1) Узнай длину каждой ломаной.
Длина ломаной № 1 равна 7 см, а ломаной № 2 — 5 см.
2) Сравни ломаные и их длины.
Отрезок. Ломаная линия
Отрезок представляет собой часть прямой линии, которая находится между двумя точками. Эти точки называют концы отрезка.
Иными словами, отрезок – это множество точек прямой линии, находящиеся между двух известных точек, которые называют концами отрезка.
Рис. 1 Отрезок на прямой
Рис. 2 Несколько отрезков на прямой
Отрезок делит прямую линию на три объекта (смотри рисунок 3):
То есть, два конца отрезка прямой являются соответственно началами двух лучей этой же прямой.
Рис. 3 Отрезок и лучи прямой
Рис. 4 Отрезок без прямой
Рис. 5 Отрезок и принадлежащие ему точки
Так, на рисунке 5 видно, что:
В последнем случае точка F хотя и лежит на одной прямой линии с отрезком AB (если вы мысленно продлите линию от точки B дальше, то увидите это), но не принадлежит ему, потому что находится не между его концами, а справа от отрезка.
Рис. 6 Отрезок и части отрезка
Построение и измерение отрезка
Произвольный отрезок можно построить двумя способами:
Рис. 7 Построение произвольного отрезка
Измерить отрезок можно:
Сравнить отрезки между собой можно при помощи циркуля или циркуля-измерителя. Для этого нужно сперва поставить иглу на один конец отрезка, а затем вторую иглу или грифельный стержень (если используется обычный чертежный циркуль) совместить со вторым концом отрезка (рисунок 8).
Рис. 8 Сравнение отрезков
На рисунке 8 видно, что:
Длину отрезка измеряют линейкой с делениями или другим измерительным инструментом.
Длина отрезка – это расстояние между концами этого отрезка.
Равные отрезки — это такие отрезки, которые имеют одинаковую длину.
На рисунке 9 измерены длины отрезков предыдущего рисунка. Проверьте, правильно ли мы сравнили эти отрезки при помощи циркуля?
Рис. 9 Измерение длины отрезка
Для этого на плоскости обозначают один конец отрезка (ставят точку), а затем при помощи линейки отмеряют необходимую длину отрезка (к примеру, 9 см), ставят точку второго конца отрезка и соединяют оба конца линией.
Рис. 10 Построение отрезка заданной длины
Отрезок — это самое короткое расстояние между двумя точками.
В этом вы можете убедиться самостоятельно на практике. Возьмите любой твердый длинный предмет, например, линейку, и шнурок. Линейка будет играть роль отрезка, а из шнурка сделайте кривую и ломаную линию, наподобие таких, какие показаны на рисунке 11, и соедините ими два конца линейки. После чего выпрямите шнурок и сравните его длину с длиной линейки.
Рис. 11 Кривая, ломаная, отрезок
Ломаная линия
Ломаная линия – это линия, которая состоит из отрезков, принадлежащих разным прямым, и эти отрезки последовательно соединены друг с другом.
Рис. 12 Ломаная линия
На рисунке 12 видно, что:
Количество звеньев у ломаной линии может быть каким угодно, бесконечным, но самое меньшее – это два звена.
Замкнутая ломаная линия – это такая ломаная, у которой совпадают точки начала и конца, то есть, которая начинается и заканчивается в одной точке.
Разомкнутая (не замкнутая) ломаная линия начинается и заканчивается в разных точках.
Рис. 12. Замкнутая и разомкнутая ломаные линии
Самопересекающаяся ломаная линия – это такая ломаная, у которой есть хотя бы два пересекающихся звена.
Самопересекающимися могут быть как замкнутые, так и разомкнутые ломаные.
Рис. 13. Самопересекающиеся ломаные линии
Длина ломаной
Урок 8. Математика 2 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Длина ломаной»
— Привет, Плюс. А чем это ты занимаешься?
— Здравствуй, Минус. Понимаешь, меня пригласила в гости буква И. Ведь мы с ней в какой-то степени родственники.
— Интересно, а что общего может быть между математическим знаком и какой-то там буквой?
— Понял. Ну а вот этот план-то тут при чем?
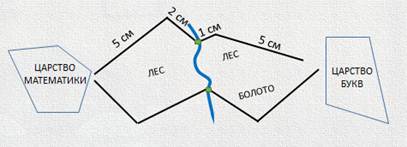
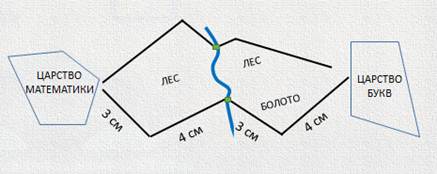
— Видишь ли, буква И живет за пределами нашего царства. Дорога предстоит долгая. Но дело в том, что к букве И можно добраться по двум разным дорогам. Вот посмотри. Передо мной точный подробнейший план местности по дороге в царство букв. И я пытаюсь понять, какая из этих двух дорог наиболее короткая.
— Не поломанными, а ломаными. Такие линии, состоящие из нескольких отрезков, в которых конец первого отрезок является началом второго, конец второго является началом третьего и так далее, называется ломаными линиями.
— Ну вот, ты сам и подсказал себе, как узнать, какая дорога короче. Ведь каждая дорога состоит из отрезков, а находить длину отрезков мы уже умеем.
Итак, можно измерить длины ломаных, используя линейку.
Измерим длину каждого звена:
Получим длину всей дороги:
А вот вторую дорогу я измерю по-другому.
— А что, есть еще какой-то другой способ нахождения длины ломаной?
А теперь измерим линейкой длину получившегося отрезка, составленного из четырех:
— Запомни, Плюсик. Длину ломаной на глазок не определишь. Для того чтобы измерить длину ломаной, надо измерить длину каждого звена, и результаты сложить.
— Да, дорогой Минус. Я это теперь хорошо запомнил. Но вот еще что меня заинтересовало. Если внимательно посмотреть на план, то можно увидеть, что не только дороги, но и контуры царств тоже представляют из себя ломаные линии.
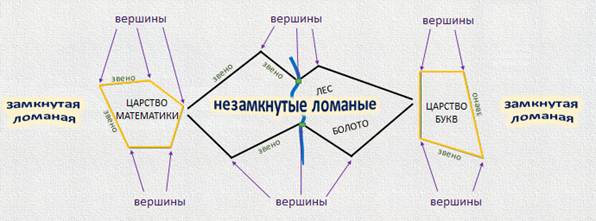
— Ух ты, как много сегодня узнали. Теперь мы знаем, что:
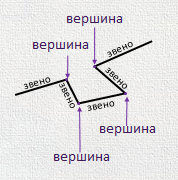
· ломаная состоит из отрезков, которые называются звенья;
· точки, в которых соединяются звенья ломаной, называются вершинами;
· чтобы найти длину ломаной, надо измерить все её звенья и результаты сложить;
· ломаные бывают незамкнутые и замкнутые.
— Ну что же, пора мне в дорогу отправляться. Буква И, наверное, уже заждалась. До свидания, Минус.
Ломаная
Определение 1. Ломаной (ломаной линией) \( \small A_1A_2. A_
Можно дать и другое определение ломаной:
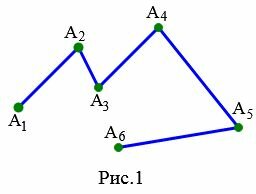 |
Невырожденная ломаная
Ломаная, описанная в определении 1 называется невырожденной ломаной.
На рисунке 1 ломаная \( \small A_1A_2A_3A_4A_5A_6 \) является невырожденной поскольку отрезки \( \small [ A_1A_2 ]\) и \( \small [ A_2A_3 ]\), \( \small [ A_2A_3 ]\) и \( \small [ A_3A_4 ]\), \( \small [ A_3A_4 ]\) и \( \small [ A_4A_5 ]\), \( \small [ A_4A_5 ]\) и \( \small [ A_5A_6 ]\) не лежат на одной прямой.
Вырожденная ломаная
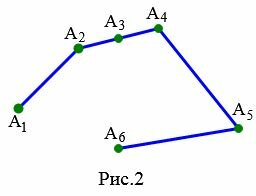 |
На рисунке 2 изображена ломаная \( \small A_1A_2A_3A_4A_5A_6 \). Эта ломаная является вырожденной поскольку отрезки \( \small [ A_2A_3 ]\) и \( \small [ A_3A_4 ]\) лежат на одной прямой.
Внимание! Если явно не указыается вырожденность ломаной, то подразумевается невырожденная ломаная.
Звенья ломаной
Звеньями называют отрезки, из которых состоит ломаная.
Вершины ломаной
Конечные точки звеньев ломаной называются вершинами.
На рисунке 1 изображена ломаная \( \small A_1A_2A_3A_4A_5A_6 \), состоящая из шести вершин: \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5, \ A_6 \).
Смежные звенья ломаной
Смежные звенья ломаной − это звенья имеющие общую вершину.
На рисунке 3 смежными звеньями ломаной \( \small A_1A_2A_3A_4A_5A_6 \) являются звенья: \( \small [ A_1A_2 ]\) и \( \small [ A_2A_3 ]\), \( \small [ A_2A_3 ]\) и \( \small [ A_3A_4 ]\), \( \small [ A_3A_4 ]\) и \( \small [ A_4A_5 ]\), \( \small [ A_4A_5 ]\) и \( \small [ A_5A_6 ]\).
Смежные вершины ломаной
Смежными вершинами ломаной называют вершины одного звена ломаной.
На рисунке 3 смежными вершинами ломаной \( \small A_1A_2A_3A_4A_5A_6 \) являются вершины: \( \small A_1\) и \( \small A_2\), \( \small A_2\) и \( \small A_3\), \( \small A_3\) и \( \small A_4 \), \( \small A_4\) и \( \small A_5\), \( \small A_5\) и \( \small A_6\).
Незамкнутая ломанная
Незамкнутым является ломаная, первая и последняя точки которой не совпадают друг с другом (Рис.3).
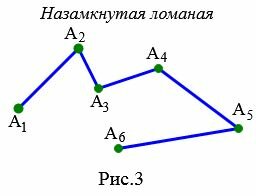 |
Замкнутая ломанная
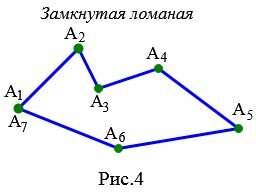 |
На рисунке 4 ломаная \( \small A_1A_2A_3A_4A_5A_6A_7 \) является замкнутым, так как точки: \( \small A_1\) и \( \small A_7\) совпадают и отрезки \( \small A_1A_2\) и \( \small A_6A_7\) не лежат на одной прямой.
Ломаная с самопересечением
Ломаная имеет самопересечение, если хотя бы два ее звена имеют общую точку, помимо общей вершины.
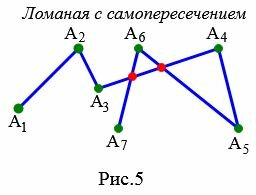 |
Ни рисунке 5 ломаная \( \small A_1A_2A_3A_4A_5A_6A_7 \) имеет самопересечение, так как звенья \( \small A_5A_6 \) и \( \small A_6A_7 \) имеют общие точки со звеном \( \small A_3A_4 \).
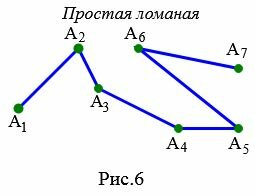
Простая ломаная
Ломаная называется простым, если не имеет самопересечений. Пример простой ломаной изображен на рисунке 6.
 |
Длина ломаной
Длина ломаной равна сумме длин всех звеньев ломаной: \( \small d= A_1A_2+A_2A_3+. +A_
Теорема. Длина ломаной больше расстояния между первым и последним точками.
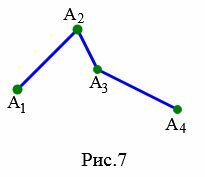 |
Доказательство. Для доказательства теоремы рассмотрим ломаную \( \small A_1A_2A_3A_4 \) с тремя звеньями (Рис.7). Так как ломаная невырождена, то вершины \( \small A_1, \ A_2, \ A_3 \) не лежат на одной прямой. Тогда имеет место неравенство треугольников:
Для точек \( \small A_1, \ A_3, \ A_4 \) имеет место следующее нестрогое неравенство:
В выражении (2) мы не применяли строгое неравенство поскольку вершины \( \small A_1, \ A_3, \ A_4 \) ломаной не являются соседними вершинами и могут лежать на одной прямой.
В неравенстве (2) вместо слагаемого \( \small A_1 A_3\) подставим сумму \( \small A_1A_2+A_2A_3 \) из (1), которая больше, чем \( \small A_1 A_3\). Тогда получим:
Поседнее неравенство означает, что длина невырожденной ломаной больше расстояния между первым и последним точками.
Аналогично доказывается теорема для ломанной с любым количеством звеньев.
Конспект по математике «Определение длины ломаной разными способами»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Конспект урока по математике.
учителя 2 класса Юдиной М.В.
Тема: Определение длины ломаной разными способами.
Тип: урок новых знаний.
Цель: учить находить длину ломаной разными способами.
Общеобразовательные: формировать умения находить длину ломаной разными способами применяя циркуль и линейку; закреплять знания о геометрических фигурах( точка, прямая, отрезок, ломаная); формировать умение работать с линейкой и карандашом, циркулем.
Коррекционно-развивающие: развивать внимание, логическое мышление, математическую речь; активизировать словарный запас; пополнить словарный запас.
Воспитательные: воспитывать интерес к предмету, аккуратность при черчении.
Мотивация. Сообщение темы урока.
Что на столе? (называние предметов для черчения: линейка, карандаш, циркуль)
Будем чертить _______ (слайд).
А) Активизация математического словаря.
Б) Понятие «ломаной».Части ломаной.
Будем учиться измерять длину ломаной.
В) Каллиграфическая минутка.
Открой книгу, страница 32. Прочитай тему урока.
Длина ломаной. Как можно узнать длину?
д) Работа с линейкой. Определение длины ломаной( 1 способ).
Возьми линейку, измерь первое звено, второе, третье.
Что нужно сделать, чтобы узнать длину? сложить.
е) Работа с циркулем. Определение длины ломаной (2 способ).
Возьми линейку и карандаш. Начерти длинную прямую.
Возьми циркуль. Измерь первое звено. Перенеси длину звена на прямую, с помощью циркуля (второе, третье звено). Получился отрезок. Сколько сантиметров отрезок? Измерь линейкой.
Измерь длину разными способами.
б) Индивидуальные карточки.
Решение примеров с именованными числами.
1 дм 3 см + 2 дм 4см =
4 дм 3 см – 1 дм 1 см =
Определяли длину ломаной.
Самооценка деятельности на уроке.
Словесное оценивание учителем.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Скоростное чтение
Курс повышения квалификации
Актуальные вопросы теории и методики преподавания в начальной школе в соответствии с ФГОС НОО
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-1555922
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
В России утвердили новый порядок формирования федерального перечня учебников
Время чтения: 1 минута
МГУ откроет первую в России магистерскую программу по биоэтике
Время чтения: 2 минуты
Время чтения: 2 минуты
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Росприроднадзор призвал ввести в школах курс по экологии
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.