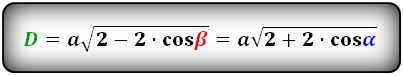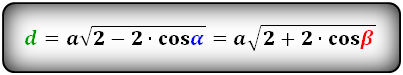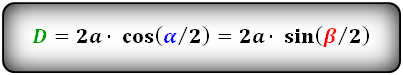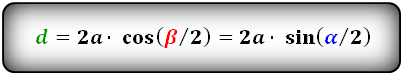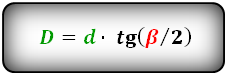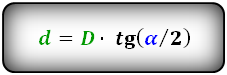Как узнать диагональ ромба
Диагонали ромба
Свойства
Диагонали ромба обладают рядом особенностей, которые позволяют использовать их в вычислениях самих по себе. Во-первых, диагонали ромба пересекаются под прямым углом, что значит, что они образуют прямоугольные треугольники во внутреннем пространстве фигуры со стороной в качестве гипотенузы. Во-вторых, узнать длину катетов этих треугольников достаточно просто, так как точкой пересечения – вершиной прямого угла, диагонали делятся на две равные части. Подставив это в теорему Пифагора, можно найти сторону ромба как половину квадратного корня из произведения диагоналей. (рис.115.2) a=√(〖d_1〗^2+〖d_2〗^2 )/2
Угол напротив каждой диагонали можно найти из равнобедренных треугольников по теореме косинуса, заменив сторону ромба на полученный радикал. (рис.115.4) cosα=(〖2a〗^2-〖d_1〗^2)/〖2a〗^2 =((〖d_1〗^2+〖d_2〗^2)/2-〖d_1〗^2)/((〖d_1〗^2+〖d_2〗^2)/2)=(〖d_2〗^2-〖d_1〗^2)/(〖d_1〗^2+〖d_2〗^2 ) cosβ=(〖2a〗^2-〖d_2〗^2)/〖2a〗^2 =(〖d_1〗^2-〖d_2〗^2)/(〖d_1〗^2+〖d_2〗^2 )
Чтобы найти высоту ромба через диагонали, надо умножить выражение, соответствующее стороне на синус найденного угла, как отношение катета к гипотенузе в прямоугольном треугольнике. (рис.115.1) h=a sinα=sinα √(〖d_1〗^2+〖d_2〗^2 )/2
Периметр ромба будет равен радикалу стороны, умноженному на четыре (коэффициенты сокращаются, и остается два), а площадь – радикалу, возведенному в квадрат и умноженному на синус угла α. P=4a=2√(〖d_1〗^2+〖d_2〗^2 ) S=a^2 sinα=(sinα (〖d_1〗^2+〖d_2〗^2 ))/4
Радиус окружности, вписанной в ромб, представляет собой перпендикуляр стороны, проведенный к точке пересечения диагоналей, при продлении которой ровно в два раза получается высота ромба. Соответственно, чтобы найти радиус вписанной окружности через диагонали ромба, нужно разделить полученную формулу для высоты на два. (рис.115.3) r=h/2=sinα √(〖d_1〗^2+〖d_2〗^2 )/4
Все формулы длины диагоналей ромба
4. Диагонали пересекаются под прямым углом (90°)
5. Диагонали являются биссектрисами
Формулы диагоналей через сторону и угол, ( D d ):
Формулы диагоналей через сторону и половинный угол, ( D d ):
Формулы диагоналей через сторону и другую диагональ, ( D d ):
Формулы диагоналей через угол и другую диагональ, ( D d ):
Формулы диагоналей через площадь ( D d ):
Формулы ромба
Для расчёта всех основных параметров ромба воспользуйтесь калькулятором.
Свойства ромба
Признаки ромба
Формулы стороны ромба
Длина стороны ромба через площадь (S) и высоту (AE)
Длина стороны ромба через площадь (S) и синус угла
Длина стороны ромба через диагонали
Длина стороны ромба через диагональ и угол
Длина стороны ромба через периметр
Формулы диагоналей ромба
Длина большой диагонали ромба через сторону и косинус острого угла(∠CDA) или косинус тупого угла(∠DAB)
Длина малой диагонали ромба через сторону и косинус острого угла(∠CDA) или косинус тупого угла(∠DAB)
Длина диагонали ромба через сторону и другую диагональ
Длина диагонали ромба через площадь и другую диагональ
Длина диагонали ромба через тангенс острого tg(∠CDA) или тупого tg(∠DAB) угла и другую диагональ
Формулы площади ромба
Площадь ромба через высоту (AE) и сторону
Площадь ромба через сторону и синус любого угла
Площадь ромба через две диагонали
Площадь ромба через большую диагональ и тангенс острого угла(∠CDA) или малую диагональ и тангенс тупого угла(∠DAB)
Формулы радиуса круга вписанного в ромб
Радиус вписанного круга в ромб через высоту ромба (AE)
Радиус вписанного круга в ромб через площадь и сторону ромба
Радиус вписанного круга в ромб через сторону и синус любого угла
Радиус вписанного круга в ромб через диагональ и синус угла
Радиус вписанного круга в ромб через две диагонали
Площадь и диагональ «d1» ромба
Свойства
Зная площадь ромба и диагональ, можно вычислить вторую диагональ, используя формулу площади, полученную из прямоугольных треугольников, образованных диагоналями. (рис.115.а) S=(d_1 d_2)/2 d_2=2S/d_1
В тех же прямоугольных треугольниках половины диагоналей являются катетами, а сторона ромба – гипотенузой, поэтому ее можно найти по теореме Пифагора, подставив вместо второй диагонали удвоенную площадь, деленную на первую диагональ. a^2=〖d_1〗^2/4+〖d_2〗^2/4 a^2=〖d_1〗^2/4+(4S^2)/(4〖d_1〗^2 ) a^2=(〖d_1〗^4+4S^2)/(4〖d_1〗^2 ) a=√(〖d_1〗^4+4S^2 )/(2〖d_1〗^2 )
Чтобы вычислить периметр ромба через площадь и диагональ, нужно умножить полученное для стороны выражение на 4 и сократить дробь. P=4a=(2√(〖d_1〗^4+4S^2 ))/〖d_1〗^2
Чтобы найти углы α и β у ромба, необходимо вернуться к прямоугольному треугольнику с диагоналями и стороной. Тангенс половины угла α будет равен отношению половины первой диагонали к половине второй диагонали. Угол β можно найти аналогичным путем, или отняв от 180 градусов угол α. tan〖α/2〗=d_1/2:d_2/2=d_1/d_2 =〖d_1〗^2/2S tan〖β/2〗=2S/〖d_1〗^2
Высота ромба связана с его стороной и углом α в прямоугольном треугольнике отношением синуса. Подставив вместо стороны ромба выражение через площадь и диагональ, можно рассчитать высоту ромба по следующей формуле. (Рис.115.1) h=sinα √(〖d_1〗^4+4S^2 )/(2〖d_1〗^2 )
Радиус окружности, вписанной в ромб, повторяет формулу высоты ромба через его площадь и диагональ, увеличивая коэффициент в знаменателе в два раза. r=sinα √(〖d_1〗^4+4S^2 )/(4〖d_1〗^2 )
Периметр ромба формула и калькулятор онлайн
Основные формулы:
Площадь ромба S можно найти по следующим формулам:
Периметр ромба через сторону
Формула для нахождения периметра ромба через сторону:
, где a — сторона ромба.
Формула вычисления периметра
1. По длине стороны
Периметр (P) ромба равняется сумме длин всех его сторон.
P = a + a + a + a
Т.к. все стороны данной геометрической фигуры равны, формулу можно представить в следующем виде (сторона умноженная на 4):
P = 4*a
Свойства ромба:
Примеры задач
Задание 1
Найдите периметр ромба, если длина его стороны составляет 7 см.
Решение:
Используем первую формулу, подставив в нее известное значение: P = 4 * 7 см = 27 см.
Задание 2
Периметр ромба равен 44 см. Найдите сторону фигуры.
Решение:
Как мы знаем, P = 4*a. Следовательно, чтобы найти одну сторону (a), необходимо периметр разделить на четыре: a = P/4 = 44 см / 4 = 11 см.
Задание 3
Найдите периметр ромба, если известны его диагонали: 6 и 8 см.
Решение:
Воспользовавшись формулой, в которой задействованы длины диагоналей, получаем:
Как найти площадь ромба если извесны его стороны?
Этих данных недостаточно. При стороне а площадь может составлять от а^2 до 0 в зависимости от угла между сторонами. А вот у правильного треугольника со стороной а площадь всегда а²√3/4.
Признаки ромба
Диагонали ромба
Диагональю ромба называется любой отрезок соединяющий две вершины противоположных углов ромба.
Формулы определения длины диагонали ромба:
d 1 = a √ 2 + 2 · cosα
d 1 = a √ 2 – 2 · cosβ
d 2 = a √ 2 + 2 · cosβ
d 2 = a √ 2 – 2 · cosα
d 1 = 2 a · cos ( α /2)
d 1 = 2 a · sin ( β /2)
d 2 = 2 a · sin ( α /2)
d 2 = 2 a · cos ( β /2)
7. Формулы диагоналей через площадь и другую диагональ:
| d 1 = | 2S |
| d 2 |
| d 2 = | 2S |
| d 1 |
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
| d 1 = | 2 r |
| sin ( α /2) |
| d 2 = | 2 r |
| sin ( β /2) |
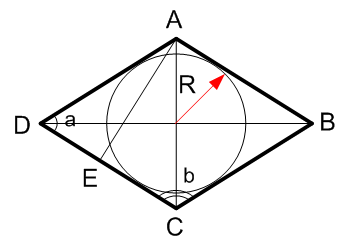
Окружность вписанная в ромб
Кругом вписанным в ромб называется круг, который примыкает ко всем сторонам ромба и имеет центр на пересечении диагоналей ромба.
Формулы определения радиуса круга вписанного в ромб:
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
| r = | S |
| 2 a |
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
| r = | √ S · sinα |
| 2 |
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
| r = | a · sinα |
| 2 |
| r = | a · sinβ |
| 2 |
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
| r = | d 1 · sin ( α /2) |
| 2 |
| r = | d 2 · sin ( β /2) |
| 2 |
6. Формула радиуса круга вписанного в ромб через две диагонали:
| r = | d 1 · d 2 |
| 2√ d 1 2 + d 2 2 |
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
| r = | d 1 · d 2 |
| 4 a |
Формулы площади ромба
Площадь ромба через высоту (AE) и сторону
Площадь ромба через сторону и синус любого угла
Площадь ромба через большую диагональ и тангенс острого угла(∠CDA) или малую диагональ и тангенс тупого угла(∠DAB)
Геометрические фигуры. Параллелограмм.
Периметры геометрических фигур
Формула периметра ромба
Периметр ромба равен произведению длины его стороны на четыре.
Найти периметр ромба
Вводить можно числа или дроби (-2.4, 5/7, …).