Как ускорить обучение нейросети

Batch-normalization

Содержание

Идея [ править ]

Пакет [ править ]

Также существует «золотая середина» между стохастическим градиентным спуском и пакетным градиентным спуском — когда просматривается только некоторое подмножество обучающей выборки фиксированного размера (англ. batch-size). В таком случае такие подмножества принято называть мини-пакетом (англ. mini-batch). Здесь и далее, мини-пакеты будем также называть пакетом.

Ковариантный сдвиг [ править ]

Пакетная нормализация уменьшает величину, на которую смещаются значения узлов в скрытых слоях (т.н. ковариантный сдвиг (англ. covariance shift)).

Ковариантный сдвиг — это ситуация, когда распределения значений признаков в обучающей и тестовой выборке имеют разные параметры (математическое ожидание, дисперсия и т.д.). Ковариантность в данном случае относится к значениям признаков.

Простой способ решить проблему ковариантного сдвига для входного слоя — это случайным образом перемешать данные перед созданием пакетов. Но для скрытых слоев нейронной сети такой метод не подходит, так как распределение входных данных для каждого узла скрытых слоев изменяется каждый раз, когда происходит обновление параметров в предыдущем слое. Эта проблема называется внутренним ковариантным сдвигом (англ. internal covariate shift). Для решения данной проблемы часто приходится использовать низкий темп обучения (англ. learning rate) и методы регуляризации при обучении модели. Другим способом устранения внутреннего ковариантного сдвига является метод пакетной нормализации.

Свойства пакетной нормализации [ править ]

Кроме того, использование пакетной нормализации обладает еще несколькими дополнительными полезными свойствами:

Описание метода [ править ]

Данные параметры настраиваются в процессе обучения вместе с остальными параметрами модели.

Тогда алгоритм пакетной нормализации можно представить так:

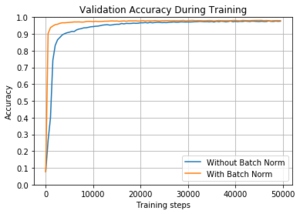
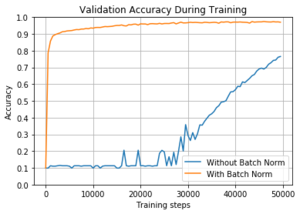
Обучение нейронных сетей с пакетной нормализацией [ править ]

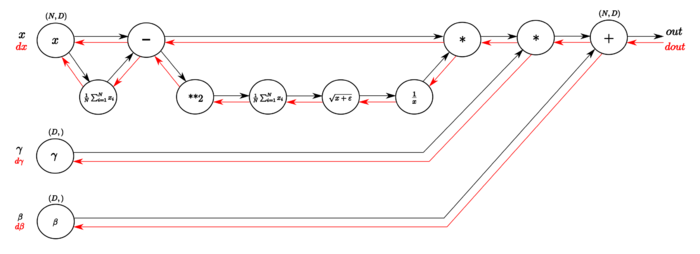
На Рисунке [math]2[/math] изображен граф вычислений слоя пакетной нормализации алгоритмом обратного распространения ошибки.

В обратном направлении вычисляются производные необходимых функций. В следующей таблице подробнее изображены шаги вычисления градиента функции потерь (иллюстрации из статьи, здесь [math]N=m[/math] и [math]D=d[/math] ):

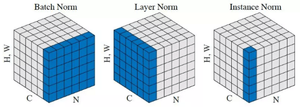
Пакетная нормализация в свёрточных сетях [ править ]

Пакетная нормализация может быть применена к любой функции активации. Рассмотрим подробнее случай аффинного преобразования с некоторой нелинейной функцией:

где [math]BN[/math] применяется отдельно к каждой размерности [math]x=Wu[/math] с отдельной парой параметров [math]\gamma^<(k)>[/math] и [math]\beta^<(k)>[/math] для каждой размерности.

Индивидуальная нормализация [ править ]

Условная пакетная нормализация [ править ]

Описание метода [ править ]

Выбор параметров нормализации [ править ]

В применении к переносу стиля [ править ]

Добавление условности [ править ]

Такой подход имеет много преимуществ по сравнению с наивным:

Когда использовать условную нормализацию? [ править ]

Во-первых, на условную нормализацию стоит обратить внимание, если вы настраиваете много сетей, решающих похожие задачи. Возможно, в этом случае вы можете использовать одну сеть с условными параметрами нормализации, зависящими от конкретной задачи. Например, при переносе стилей вместо [math]S[/math] сетей вы настраиваете одну сеть с [math]S[/math] наборами параметров нормализации.

Во-вторых, если вы подозреваете, что информация о структуре входных векторов имеет значение для выхода. Например, имеет смысл «слить» лингвистическую информацию и характеристики изображения для задачи ответа на визуальные вопросы (англ. Visual Question Answering, VQA).

Однако во всех случаях надо помнить, что полученные алгоритмы для разных задач будут различаться лишь параметрами свёртки и сжатия. Иначе говоря, если ваши задачи нельзя выразить аффинной комбинацией параметров сети после нормализации, условная нормализация не поможет.

Пример [ править ]

Реализации [ править ]

Приведем пример [11] применения пакетной нормализации с использованием библиотеки TensorFlow на языке программирования Python [12] :

Модификации [ править ]

Существует несколько модификаций и вариаций метода пакетной нормализации:

Источник

Ускорение обучения, начальные веса, стандартизация, подготовка выборки

Без знания этих моментов, провести качественное обучение НС практически невозможно. Поэтому, для полноты картины, мне придется дать некоторый теоретический материал, чтобы вы могли ориентироваться в этих вопросах. Возможно, вам это покажется несколько скучным, но, знаете, яркие эффекты – это лишь вершина айсберга, в основании очень много подготовительного материала и кропотливой работы по проектированию и обучению сетей. Так что, если вы решили пойти по этому пути и начать работать в данной области, то без базовой математической подготовки, знания основных моментов и наработки опыта, тут никуда.

Общего решения этой проблемы нет. Поэтому на практике запускают алгоритм обучения с разными начальными значениями весовых коэффициентов. Тем самым мы, как бы выбираем разные отправные точки на функции E в надежде, что одно из решений достигнет глобального минимума. Хотя, точно узнать: достигли мы дна или нет не представляется возможным. Поэтому процесс обучения останавливают, если достигается требуемое качество работы НС.

Отсюда получаем рекомендацию обучения №1:

Запускать алгоритм для разных начальных значений весовых коэффициентов. И, затем, отобрать лучший вариант. Начальные значения генерируем случайным образом в окрестности нуля, кроме тех, что относятся к bias’ам.

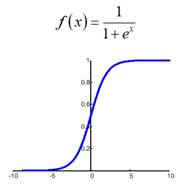
У вас может возникнуть вопрос: почему начальные значения весов нужно брать малыми? Смотрите, допустим, используется логистическая функция активации:

Если веса изначально буду значимыми, то часто суммарный сигнал на входе нейронов будет оказываться большим по модулю:

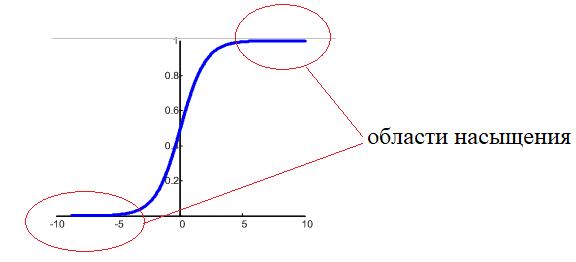
И мы попадаем на пологий участок функции активации. К чему это потом приводит? В процессе обучения градиент этого участка будет мал, а значит, веса будут медленно изменяться, что приведет к торможению обучения НС в целом. Чтобы этого избежать, мы, как раз и выбираем веса с малыми случайными значениями, и оказываемся на более выгодном крутом участке кривой. Bias же (смещения разделяющих гиперплоскостей) могут быть и с большими значениями, т.к. они отвечают именно за смещение разделяющей гиперплоскости и оно может быть значительным.

Другая проблема градиентных алгоритмов – медленная сходимость на пологих участках функции:

О первых двух я рассказывал на занятии по градиентному спуску:

Почему так важно знать об этих методах оптимизации? Дело в том, что многие пакеты реализации и обучения НС, например,

позволяют использовать их для ускорения и улучшения обучения. Чаще всего применяется оптимизация по Нестерову и Adam’у. Позже, когда мы будем рассматривать один из этих пакетов, я покажу где и как настраиваются эти параметры.

Итак, рекомендация обучения №2:

Запускаем алгоритм обучения с оптимизацией по Adam или Нестерову для ускорения обучения НС.

Входные значения

Стоит ли нам подавать значения этой выборки так как они есть? Так делать не рекомендуется. В общем случае, среди этих величин могут оказаться большие значения и они нас сразу переместят в область насыщения функции активации, где производная практически равна нулю:

Поэтому на практике выполняют предварительную стандартизацию входных значений, например, по формуле:

Здесь max, min – максимальное и минимальное значения входных данных по всему обучающему множеству. В результате, входные данные при обучении будут находиться в диапазоне от 0 до 1.

И здесь начинающие нейронщики часто делают одну важную ошибку. После обучения НС в режиме ее эксплуатации забывают о нормализации данных на ее входах. Раз уж сеть обучена на нормированных значениях, то и потом, при ее непосредственной работе, данные также нужно нормировать. Об этом забывать не стоит. И, кроме того, нормировку следует делать через те же самые параметры min и max, которые были использованы в обучающей выборке! А не пересчитывать их заново!

Рекомендация обучения №3:

Выполнять нормировку входных значений и запоминать нормировочные параметры min, max из обучающей выборки.

Как создавать и подавать обучающую выборку

Следующий важный вопрос: что из себя должна представлять обучающая выборка? Какие данные в нее следует поместить? Ответить можно так: чем больше разных наблюдений будет при обучении, тем выше качество работы сети. Здесь ключевое слово – разных, то есть, выборка должна охватывать самые разные «ситуации» в процессе обучения и эти «ситуации» должны появляться с равной частотой. Например, представьте, что вы учитесь водить машину, но ваш инструктор выбирает перекрестки только со светофором. Как думаете, сможете вы себя потом уверенно чувствовать на нерегулируемых перекрестках? Вряд ли. Я бы не смог. С нейросетью также: если в процессе эксплуатации будут попадаться входные данные, сильно отличающиеся от обучающей выборки, то высока вероятность возникновения ошибки. Или, другой пример. Ваш инструктор для «галочки» лишь показал как проезжать нерегулируемые перекрестки, но вы все равно, в основном проезжали по регулируемым со светофором. Здесь качество обучения также будет невысоким, т.к. навыка проезда обычных перекрестков будет недостаточно. Поэтому желательно, чтобы в обучающей выборке с равной частотой встречались самые разные данные, описывающие какие-то характерные, особенные, частные ситуации.

Рекомендация обучения №4:

Помещать в обучающую выборку самые разнообразные данные примерно равного количества.

Хорошо, с этим разобрались, но какой объем обучающей выборки N следует брать? По идее, чем больше, тем лучше. Например, в литературе отмечают, что при классификации картинок (например, на мужчин и женщин, или кошек и собак и т.п.) необходимо по 5 000 000 наблюдений для каждого класса, тогда можно достичь хороших результатов различения. Если увеличить этот объем до 10 000 000, то есть шанс обучить нейросеть распознавать образы лучше человека. Вас, возможно, удивят такие большие цифры? Да, это так, данные для обучения – это как нефть «черное золото» для нашей экономики, они ценятся очень высоко, а их подготовка может потребовать немалых ресурсов и времени. Это еще одна причина, по которой нейронные сети лишь недавно завоевали свое место под солнцем: раньше практически невозможно было получить столько реальных данных. Теперь же, сеть Интернет, в частности, социальные сети, предоставляют весьма богатый материал.

Итак, предположим, что мы создали обучающую выборку и собираемся приступить к обучению. Здесь возникает новый вопрос: как ее подавать на вход сети? В самом простом варианте, мы сначала перемешиваем наблюдения в выборке (чтобы они шли в случайном порядке), а затем поочередно подаем на вход. При этом для каждого наблюдения выполняем корректировку весовых коэффициентов. Именно так мы делали на предыдущем занятии.

Но это не самый лучший вариант. Было замечено, что в процессе обучения часть наблюдений дают небольшой положительный прирост весовых коэффициентов, часть – небольшой отрицательный. В сумме они практически компенсируют друг друга и изменение весов практически не происходит. И лишь некоторая часть наблюдений из выборки приводит к их заметному изменению. Чтобы не «крутить» вхолостую весовые коэффициенты, коррекцию выполняют не сразу для каждого наблюдения, а после прогонки через сеть некоторого их количества. Такое множество получило название batch или, в последнее время чаще стали говорить mini—batch. А вся выборка получила название эпоха. Так вот, прогоняя mini-batch через сеть, суммируют локальные градиенты на каждом нейроне (я думаю вы помните, что это такое из предыдущего занятия), а затем, корректируют веса по результирующей их сумме. В процессе такого суммирования небольшие положительные и отрицательные значения будут скомпенсированы и останется полезное смещение, которое и приведет к изменению весов в пределах mini-batch.

Такая идея позволила сократить время обучения в разы, что очень важно, так как для больших НС общее время обучения составляет иногда дни, недели и даже месяцы. Поэтому сокращение этого времени в несколько раз открывает новые горизонты применения НС.

Когда целесообразно разбивать выборку на серию mini-batch? Считается, что для этого общее число выборки должно составлять от нескольких тысяч и более. Если наблюдений меньше, порядка тысячи, то ее можно воспринимать как один единственный mini-batch.

Итак, мы получаем рекомендацию обучения №5:

Наблюдения на вход сети подавать случайным образом, корректировать веса после серии наблюдений, разбитых на mini-batch.

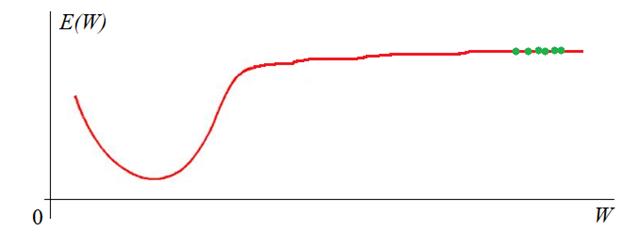
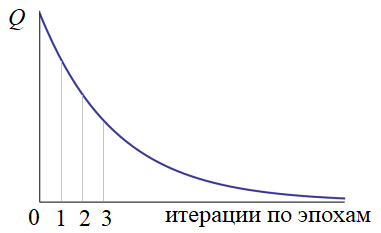
Значение критерия качества вычисляется только после прогонки всей эпохи. Если оно нас не устраивает (как правило, так и есть), то наблюдения снова тасуются случайным образом и обучение продолжается. В конце каждой эпохи снова и снова пересчитывается критерий качества. Получается такой график:

Конечно, это идеализированный график. В реальности он, конечно, не такой гладкий и монотонный. Нередки случаи когда он может внезапно возрастать. Но об этом мы поговорим в другой раз. На следующем продолжим рассматривать эти, достаточно важные вопросы, без знания которых начинать работать с нейросетями не имеет особого смысла.

Источник

Как ускорить обучение нейросети

В докладе, на примере многослойных полносвязных нейронных сетей рассматривается проблема долговременности их обучения. Предложены возможные методы увеличения скорости обучения сетей: управление процедурами вычисления и изменения весовых коэффициентов, реорганизация объектов в распознаваемых классах.

Искусственные нейронные сети находят все более широкое применение в решении задач искусственного интеллекта. Они уже доказали свою способность решать такие задачи как ассоциативный поиск, кластирование и распознавание образов.

На сегодняшний день в распоряжение разработчика предоставлено большое количество различных моделей нейронных сетей и алгоритмов их обучения [1, 2, 3]. И хотя постоянно ведутся научные исследования в области совершенствования существующих и создания новых моделей и обучающих алгоритмов, теория нейронных сетей пока остается слабо формализованной. Однако, уже на данном этапе четко прорисовываются два основных этапа создания нейронного вычислителя: структурный и параметрический синтез. В рамках первого этапа перед разработчиком ставятся задачи: определения модели сети, определение ее структуры, выбор алгоритма обучения. Параметрический синтез включает в себя процессы обучения нейронной сети и верификации полученных результатов. Причем в зависимости от результатов верификации возникает необходимость возврата на различные стадии структурного или параметрического синтеза, т.о. становится очевидной итеративность процесса проектирования нейронного вычислителя.

Слабая формализованность этих этапов приводит к тому, что разработчику, проектирующему нейронный вычислитель, приходится сталкиваться с решением некоторых проблем. Например, на этапе структурного синтеза, при проектировании нейровычислителя, решающего нестандартную задачу, приходится прилагать значительные усилия для выбора модели сети, её внутренней структуры и способа обучения. Проблемой параметрического синтеза сетей является трудоемкость их обучения. Если решать реальные задачи, учитывая все возможные факторы, то время обучения нейронной сети для такой задачи оказывается достаточно продолжительным. Но при решении некоторых задач требуется затратить как можно меньше времени на этот процесс, например, работа в реальном масштабе времени.

Данная статья ставит своей задачей предложить возможные методы уменьшения времени, затрачиваемого на обучение многослойных нейронных сетей с обратным распространением ошибки. В качестве таких методов предлагаются: управление процедурами изменения и вычисления весовых коэффициентов, реорганизация объектов в распознаваемых классах. В [4] были предложены два возможных пути решения этой задачи. Первый основывался на выборе определенного функционального базиса нейронной сети. Второй метод управлял значением шага изменения весов сети, рассматривая его с точки зрения центробежной силы и, корректируя его таким образом, чтобы его вектор всегда был направлен на оптимум множества весовых коэффициентов.

В предлагаемой работе поставленная задача рассматривается с точки зрения переобучения нейронной сети. В большинстве случаев нейронную сеть обучают, пока ее ошибка не станет равной нулю. Это приводит порой к неоправданным затратам драгоценных ресурсов времени, хотя для решения большей части задач достаточно, чтобы эта ошибка не превышала определенного значения.

Иногда степень достаточности определяется исходя из условий задачи и искомого результата. Однако, в большинстве случаев этот процесс протекает на интуитивном уровне и руководствующий принцип не фиксируется сознанием в достаточной мере. На самом деле этот момент является одним из самых важных в решении задач подобного типа, и оптимальное значение варьируемого параметра может зависеть от многих исходных величин и ограничений накладываемых на решение задачи. Таким образом, появляется необходимость в формализации данного принципа; в дальнейшем — Принципа Достаточности (ПД).

Обучение с учетом Принципа Достаточности

Как уже говорилось ранее, нейронные сети используются для решения ряда задач искусственного интеллекта. Рассмотрим обучение многослойной нейронной сети с обратным распространением ошибки в рамках решения задач классификации [5].

В процессе обучения нейронных сетей, в числе прочих, можно выделить два вида ошибки, назовем их глобальной и локальной. Выражение для вычисления локальной ошибки имеет следующий вид:

где e_k – элементарная ошибка k-го нейрона выходного слоя сети, m – число нейронов в выходном слое сети.

Глобальная ошибка сети вычисляется по следующей формуле:

где E_i – локальная ошибка нейронной сети на i-м наборе, n – число обучающих наборов.

Идеально обученной, считается такая сеть, которая полностью повторяет ОВ [6], т.е. ее глобальная ошибка равна нулю. Но обучение нейронной сети до такой степени представляет собой очень трудоемкую задачу, а нередко и вовсе неразрешимую. Эти трудности обычно связаны с тем, что разные классы имеют похожие объекты, и чем таких объектов больше и чем больше они похожи, тем труднее будет обучить нейронную сеть.

Суть ПД заключается в отказе от обязательного стремления к Идеалу при поиске решения конкретной задачи. Рассматривая эту проблему с точки зрения ПД в рамках глобальной и локальной ошибки, можно сказать, что далеко не всегда необходима 100%-я точность распознавания. Иногда, для того чтобы отнести исследуемый объект к заданному классу, достаточно, чтобы ошибка сети на данном наборе не превышала некоторого &delta.

Минимальное значение &delta зависит от характера обучающей выборки. В качестве параметров характеризующих ОВ рассмотрим ее полноту, равномерность и противоречивость. Полнота выборки характеризуется обеспеченностью классов обучающими наборами; количество обучающих наборов для класса должно в 3-5 раз больше, чем используемое в наборе число признаков класса [7]. Пусть величина, характеризующая полноту выборки, вычисляется следующим образом:

где N_F – число классов удовлетворяющих указанному условию, N – общее число классов.

где k – количество классов. Вычислим мат-ожидания для величин &Delta _Ci и [C_i] при условии, что они равновероятны и назовем их соответственно R _&Delta и N_cp :

Тогда равномерность выборки будет вычисляться по формуле:

Противоречивость – это процент противоречивых наборов в ОВ; противоречивыми считаются наборы (объекты), обладающие одинаковыми признаками, но относящиеся к разным классам. Таким образом, противоречивость есть:

где N_ПР – число противоречивых наборов, N – общее число наборов в ОВ.

Очевидно, что чем меньше противоречивость ОВ и выше её равномерность, тем уже может быть интервал &delta.

Однако, в процессе обучения объекты классов, попадая в интервал &delta, ложатся неравноудаленно от Эталона класса (рис. 2.1). Дифференцирование этих ситуаций позволит улучшить качество обучения сети, поскольку позволит корректировать веса с учетом удаленности реакции сети от эталонной. В данном случае, расстояние до эталона будет определять величину градиента изменения веса. Для этого необходимо либо разбить область  на отрезки и каждому из них поставить в соответствие значение градиента (Рис. 2.2), либо задать на этом интервале функцию a(t)=F(x) (Рис. 2.3).

Таким образом, предполагалось уменьшить число итераций обучения нейронной сети при заданной точности распознавания элементов выборки. Результатом применения этого метода стало то, что функция ошибки сети E из колебательной становилась фактически монотонно убывающей.

Коррекция шага изменения весовых коэффициентов

В оригинальном варианте алгоритма обратного распространения ошибки [8] формула изменения весовых коэффициентов, для пары нейронов i, j (Рис. 1), выглядит следующим образом:

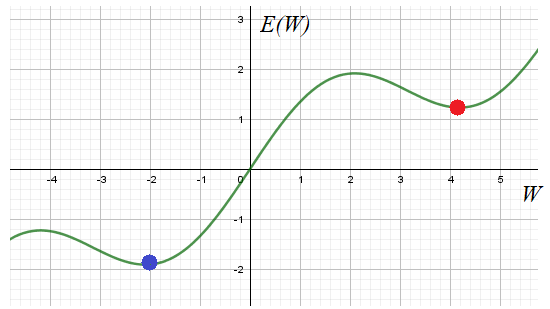
где E_j – ошибка j-го нейрона, A_i – уровень активации i-го нейрона, а &alpha – шаг изменения веса. Здесь &alpha – величина постоянная, однако очевидно, что если он будет слишком мал, то обучение будет проходить очень медленно. Если же &alpha велик — то, в момент достижения точки минимума (глобального или локального) функции ошибки E=f(W) (E – глобальная ошибка сети, W – множество весовых коэффициентов сети) (Рис. 2), сеть не сможет в нее попасть и будет бесконечно долго колебаться вокруг нее, производя бесконечные пересчеты множества весов и ухудшая свои показатели.

Предлагаемый метод динамического управления шагом изменения весовых коэффициентов нейронной сети в процессе ее обучения позволяет обеспечить максимальную скорость уменьшения ошибки сети E на всех участках графика E=f(W).

Реорганизация распознаваемых классов

Еще одним методом ускорения обучения нейронных сетей является реорганизация множества распознаваемых классов. В зависимости от того, на сколько ОВ противоречива и неравномерна мы можем объединять классы между собой либо образовывать новые.

Рассмотрим ситуацию с неравномерной ОВ, здесь параметрами ПД выступают точность интерпретации исходных данных и размерность самой нейронной сети. Точность представления данных обуславливается формируемыми классами.

Для многослойных нейронных сетей типа Back Propagation зависимость этих характеристик заключается в следующем: количество распознаваемых классов однозначно определяет число нейронов в выходном слое сети, что косвенно определяет и количество нейронов в ее скрытых слоях. Таким образом, сокращение числа классов ведет к уменьшению размерности нейронной сети, а чем меньше сеть, тем быстрее она учится.

Однако большинство реальных задач, решаемых на нейронных сетях, не допускают таких потерь в точности классификации. Таким образом, этот метод может быть применен только для задач, не обладающих жесткими ограничениями по точности.

Формирование новых классов производится в седующих случаях:

1. если в классе кроме объектов, приближенных к эталону класса и имеющих низкую дисперсию – Правила, существуют объекты удаленные от эталона и (разрозненно) расположенные вблизи его границ – Исключения;

2. если дисперсия внутри класса велика и невозможно чётко определить эталон.

Исключения и нечёткие классы повышают противоречивость ОВ, их наличие может говорить о неверном разбиении пространства объектов на классы. Решением данной проблемы может быть перемещение Исключений в другие классы либо образование новых классов с меньшей величиной дисперсии.

Таким образом, мы можем повысить скорость обучения нейронной сети либо за счет сокращения числа распозаваемых классов, либо, понижая противоречивость ОВ путем перемещения объектов между классами и образуя новые классы. В первом случае скорость обучения увеличивается из-за уменьшения размерности нейронной сети, во втором – из-за повышения качества ОВ.

Итак, в статье было предложено три возможных способа увеличения скорости обучения многослойных нейронных сетей. Также отметим здесь, что способ [4], основанный на выборе функционального базиса нейронной сети, рассматривает эту проблему с точки зрения увеличения скорости вычислений. Описанные же в статье первые два метода рассматривают задачу ускорения обучения, как задачу уменьшения числа итераций обучения, а последний предполагает оба варианта. Исходя из этих предпосылок, можно сделать вывод о том, что в рамках быстрого развития современного аппаратного обеспечения, предложенные в данной работе методы являются более перспективными в проблеме ускорения обучения нейронных сетей.

Все представленные методы были успешно применены на практике, при решении задачи прогнозирования остатков на банковских счетах. Наибольший выигрыш в количестве итераций дали метод коррекции шага и сокращение числа распознаваемых классов. Так, коррекция величины шага позволила сократить число итераций на порядок, а время обучения практически в два раза.

1. В.А. Крисилов, Д.Н. Олешко, А.В. Трутнев. Применение нейронных сетей в задачах интеллектуального анализа информации. //Труды Одесского политехнического университета, Вып.2 (8). 1999, с. 134

2. Авеньян Э.Д. Алгоритмы настройки многослойных нейронных сетей.//Автоматика и телемеханика-1995-N 5. С.106-118.

3. Минский М., Пейперт С. Персептроны. М.: МИР, 1971. с. 261.

4. P. Patrick. Minimisation methods for training feedforward Neural Networks. //NEUARAL NETWORKS, 1994, Volume 7, Number 1, P. 1-11

Источник