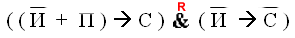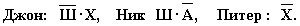Как упростить логическое выражение
Упрощение логических выражений
Основная образовательная задача урока – научить учащихся умению упрощать логические выражения, правильно определять порядок выполнения операций в логическом выражении, устанавливать связи между различными частями сложных логических выражений, умение выбирать лучший вариант решения.
Под упрощением формулы, не содержащей операций импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая либо содержит по сравнению с исходной меньшее число операций конъюнкции и дизъюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных.
Обозначим: X – логическое высказывание, 
– инверсия, & – конъюнкция, 
– дизъюнкция, 
– импликация, 
– эквиваленция.
Применение основных законов логики для упрощения логических выражений.
Представленные примеры демонстрируют основные приемы упрощения логических выражений.
Упростить логическое выражение:
1) 
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций:
Воспользуемся распределительным законом и вынесем за скобки общий множитель, затем операцией переменной с ее инверсией.
Воспользуемся распределительным законом и вынесем за скобки общий множитель, затем операцией переменной с ее инверсией, затем операцией с константами.
2) 
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций. В выражении присутствуют два выражения в скобках, соединенных дизъюнкцией. Сначала преобразуем выражения в скобках.
В первой скобке воспользуемся распределительным законом, во второй скобке – раскроем инверсию по правилу де Моргана и избавимся от инверсии по закону двойного отрицания.
Воспользуемся операцией переменной с ее инверсией.
3) 
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций. В выражении присутствуют два выражения в скобках, соединенных конъюнкцией. Сначала преобразуем выражения в скобках.
Раскроем инверсию по правилу де Моргана, избавимся от инверсии по закону двойного отрицания.
Воспользуемся переместительным законом и поменяем порядок логических сомножителей.
Применим закон склеивания 
Воспользуемся распределительным законом, затем операцией переменной с ее инверсией, затем операцией с константами.
4) 
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций.
В выражении присутствует импликация. Сначала преобразуем импликацию 
.
Воспользуемся правилом де Моргана, затем законом двойного отрицания, затем раскроем скобки.
Применим закон идемпотенции и перегруппируем логические слагаемые.
Воспользуемся распределительным законом и вынесем за скобки общий логический множитель.
Воспользуемся операцией с константами.
5) 
Рассмотрим 3 способа упрощения этого логического выражения.
1 способ. Перепишем выражение с помощью более привычных операций умножения и сложения.
Воспользуемся распределительным законом и раскроем скобки, затем операцией переменной с ее инверсией и законом идемпотенции.
Воспользуемся распределительным законом и раскроем скобки, затем операцией переменной с ее инверсией.
Воспользуемся законом идемпотенции.
2 способ. Перепишем выражение с помощью более привычных операций умножения и сложения.
Воспользуемся законом склеивания 
Воспользуемся операцией переменной с ее инверсией.
3 способ. Перепишем выражение с помощью более привычных операций умножения и сложения.
Повторим второй сомножитель 
, что разрешено законом идемпотенции.
Сгруппируем два первых и два последних сомножителя.
Воспользуемся законом склеивания 
6) 
Рассмотрим 2 способа упрощения этого логического выражения.
1 способ. Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций.
Воспользуемся распределительным законом и вынесем общий логический множитель за скобки.
2 способ. Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций.
Введем вспомогательный логический сомножитель 
Сгруппируем 1 и 4, 2 и 3 логические слагаемые. Вынесем общие логические множители за скобки.
Воспользуемся операцией с константами и операцией переменной с ее инверсией.
Получили два логических выражения:
Теперь построим таблицы истинности и посмотрим, правильно ли упрощено логическое выражение
| X | Y | Z |  |  |  |  |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| X | Y | Z |  |  |  |  |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| X | Y | Z |  |  |  |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 1 |
| X | Y | Z |  |  |  |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Как видно из сравнения таблиц истинности формулы являются равносильными.
Как упростить логическое выражение
Логические операции (конъюнкция, дизъюнкция, инверсия)
Таблица истинности: К онъюнкция (логическое умножение, логическое И) обозначается /\
(например, А /\ В) либо & (например, А & В); в языках программирования обозначение «And».
Таблица истинности: Дизъюнкция (логическое сложение, логическое ИЛИ) обозначается \/ (например, А \/ В);
в языках программирования обозначение «Or».
Инверсией двух высказываний называется новое высказывание, которое истинное тогда и только тогда, когда исходное высказывание ложно.
Название логической операции
Конъюнкция, логическое умножение
Дизъюнкция, логическое сложение
тогда и только тогда, когда
эквивалентность, эквиваленция, равнозначность
Соединим оба утверждения в одно высказывание:
Составим таблицу истинности на полученное высказывание:
Учитывая то, что предположения двух друзей подтвердились, а предположения третьего неверны, запишем и упростим истинное высказывание
Высказывание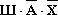 
истинно только при Ш=1, А=0, Х=0.
Пусть дана таблица истинности для некоторой логической функции Z(X,Y):
Построим истинностную таблицу сложного высказывания :
Очевидно, истинностная таблица будет содержать 
строк. Скобки применяются, если нарушаются естественный порядок операций: отрицание, конъюнкция, дизъюнкция, импликация, двойная импликация. Скобки (А ® В) указывают на то, что сначала нужно выполнить импликацию, затем найти (А ® В) Ù С. Скобки в выражении 
можно опустить. Заключительной операцией в построении истинностной таблицы для S будет дизъюнкция двух высказываний: (А ® В) Ù С и .