Как упрощать выражения видеоурок

Как упрощать выражения видеоурок

Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту

В этом занятии познакомимся с понятием «подобные слагаемые» и на примерах научимся выполнять приведение подобных слагаемых, упрощая, таким образом, буквенные выражения.

Выясним смысл понятия «упрощение». Слово «упрощение» образовано от слова «упрости́ть». Упрости́ть – значит сделать простым, проще. Следовательно, упростить буквенное выражение – это сделать его более коротким, с минимальным количеством действий.

Рассмотрим выражение 9х + 4х. Это буквенное выражение, которое является суммой. Слагаемые здесь представлены в виде произведений числа и буквы. Числовой множитель таких слагаемых называется коэффициентом. В этом выражении коэффициентами будут числа 9 и 4. Обратите внимание, множитель, представленный буквой – одинаковый в обоих слагаемых данной суммы.

Вспомним распределительный закон умножения:

Чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и полученные произведения сложить.

В общем виде записывается так: (а + b) ∙ с = ac + bc.

Этот закон выполняется в обе стороны ac + bc = (а + b) ∙ с

Применим его к нашему буквенному выражению: сумма произведений 9х и 4х равна произведению, первый множитель которого равен сумме 9 и 4, второй множитель – х.

9 + 4 = 13, получается 13х.

9х + 4 х = (9 + 4)х = 13х.

Вместо трех действий в выражении осталось одно действие – умножение. Значит, мы сделали наше буквенное выражение проще, т.е. упрости́ли его.

Слагаемые 9х и 4х отличаются только своими коэффициентами – такие слагаемые называют подобными. Буквенная часть у подобных слагаемых одинаковая. К подобным слагаемым относятся также числа и равные слагаемые.

Важно отметить, что слагаемые, у которых равны коэффициенты, а буквенные множители различны, подобными не являются, хотя к ним полезно иногда применить распределительный закон умножения, например, сумма произведений 5х и 5у равна произведению числа 5 и суммы х и у

Упрощая выражение, мы находили суммы подобных слагаемых, в математике это называют приведением подобных слагаемых.

Если приведение подобных слагаемых вызывает затруднение, можно придумать к ним слова и складывать предметы.

Например, рассмотрим выражение:

На каждую букву берем свой предмет: b-яблоко, с-груша, тогда получится: 2 яблока минус 5 груш плюс 8 груш.

Можем из яблок вычесть груши? Конечно, нет. А вот к минус 5 грушам прибавить 8 груш можем.

Приведем подобные слагаемые –5 груш + 8 груш. У подобных слагаемых буквенная часть одинаковая, поэтому при приведении подобных слагаемых достаточно выполнить сложение коэффициентов и к результату дописать буквенную часть:

Возвращаясь к нашему буквенному выражению, имеем –5 с + 8с = 3с. Таким образом, после приведения подобных слагаемых получим выражение 2b + 3с.

Итак, на этом занятии Вы познакомились с понятием «подобные слагаемые» и научились упрощать буквенные выражения путем приведения подобных слагаемых.

Источник

Как упрощать выражения видеоурок

Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту

В этом уроке Вы познакомитесь с буквенной записью различных свойств сложения и вычитания, кроме того узнаете, как можно упростить числовое или буквенное выражение, используя эти свойства.

Все свойства сложения и вычитания можно записать с помощью букв, т.е. в виде буквенных выражений.

1. Переместительное свойство сложения, которое звучит следующим образом: При перестановке слагаемых сумма не меняется.

Можно записать так: а + b = b + а

В этом равенстве буквы а и b могут принимать любые натуральные значения и значение ноль тоже.

2. Сочетательное свойство сложения:

Чтобы к числу прибавить сумму двух чисел, можно к этому числу сначала прибавить первое слагаемое, а затем к полученной сумме прибавить второе слагаемое.

Данное свойство с помощью букв записывается таким образом:

a + (b + c) = (a + b) + c = а + b + с

Здесь а, b, с также могут принимать любые натуральные значения и ноль.

3. Свойство нуля при сложении.

Если к числу прибавить ноль, то получится само число. Если к нулю прибавить какое- либо число, то получится прибавленное число.

С помощью букв это свойство можно записать таким образом a + 0 = 0 + a = а.

И здесь буква а может принимать любое значение.

4. Свойство вычитания суммы из числа.

Чтобы вычесть сумму двух чисел из данного натурального числа, необходимо сначала вычесть из этого числа первое слагаемое, а потом из полученной разности – второе слагаемое.

Данное свойство с помощью букв записывается следующим образом:

Здесь обязательно должно выполняться условие, что сумма в + с меньше или равна а. Данная запись выглядит так: b + с § 2 Упрощение выражений

Давайте выполним несколько заданий, используя буквенную запись свойств сложения и вычитания.

Запишите сочетательное свойство сложения с помощью букв х, у, с.

Замените буквы их значениями х = 12, у = 18, с = 20 и проверьте получившееся числовое равенство.

Сочетательное свойство сложения звучит следующим образом: чтобы к числу прибавить сумму двух чисел, можно к этому числу сначала прибавить первое слагаемое, а затем к полученной сумме прибавить второе слагаемое.

С помощью букв х, у и с, можем записать его в виде: х + (у + c) = (х + у) + c.

Теперь проверим данное равенство, подставив вместо х число 12, вместо у число 18, вместо с число 20, получаем следующую запись:

12 + (18 + 20) = (12 + 18) + 20

Проверим ее: в левой части равенства сумма 18 и 20 равна 38, прибавив к 12 тридцать восемь получим 50.

Теперь вычислим правую часть равенства: 12 + 18 равно 30, затем 30 + 20 получится 50. Т.е. равенство верное.

Упростите выражение 137 – с – 27.

Представим данное выражение в виде: 137 – (с+27).

С помощью переместительного свойства сложения перепишем равенство в виде:

Теперь с помощью свойства вычитания суммы из числа, имеем:

Таким образом, на этом уроке Вы познакомились с буквенной записью свойств сложения и вычитания, а также узнали, как можно упростить числовое или буквенное выражение, используя эти свойства.

Источник

Урок «Упрощение выражений»

Краткое описание документа:

Видеоурок «Упрощение выражений» раскрывает некоторые возможности операций при выполнении преобразования выражений. В ходе видеоурока на примерах подробно раскрывается суть распределительного свойства умножения, а также сочетательного свойства, приводится много примеров, помогающих усвоить материал. С помощью видеоурока учитель имеет возможность наглядно, понятно для учеников представить материал. При этом ему не нужны другие пособия, чтобы сформировать понятие. С помощью видеоурока можно быстрее достичь целей урока, повысить его эффективность.

При составлении видео были использованы инструменты, которые воздействуют на мыслительные процессы ученика, стимулируя запоминание и понимание материала. Представление текста в цвете помогает быстрее его запомнить, выделить важные понятия, формируя понимание. С помощью анимационных эффектов достигается последовательное изложение материала, возможность подчеркнуть важные особенности в решении задач, сделать решения более наглядными. С помощью иллюстраций легче наглядно представить изучаемый материал. Так как видео озвучено, это позволяет дополнить его комментариями учителя, которые помогают лучше усвоить материал.

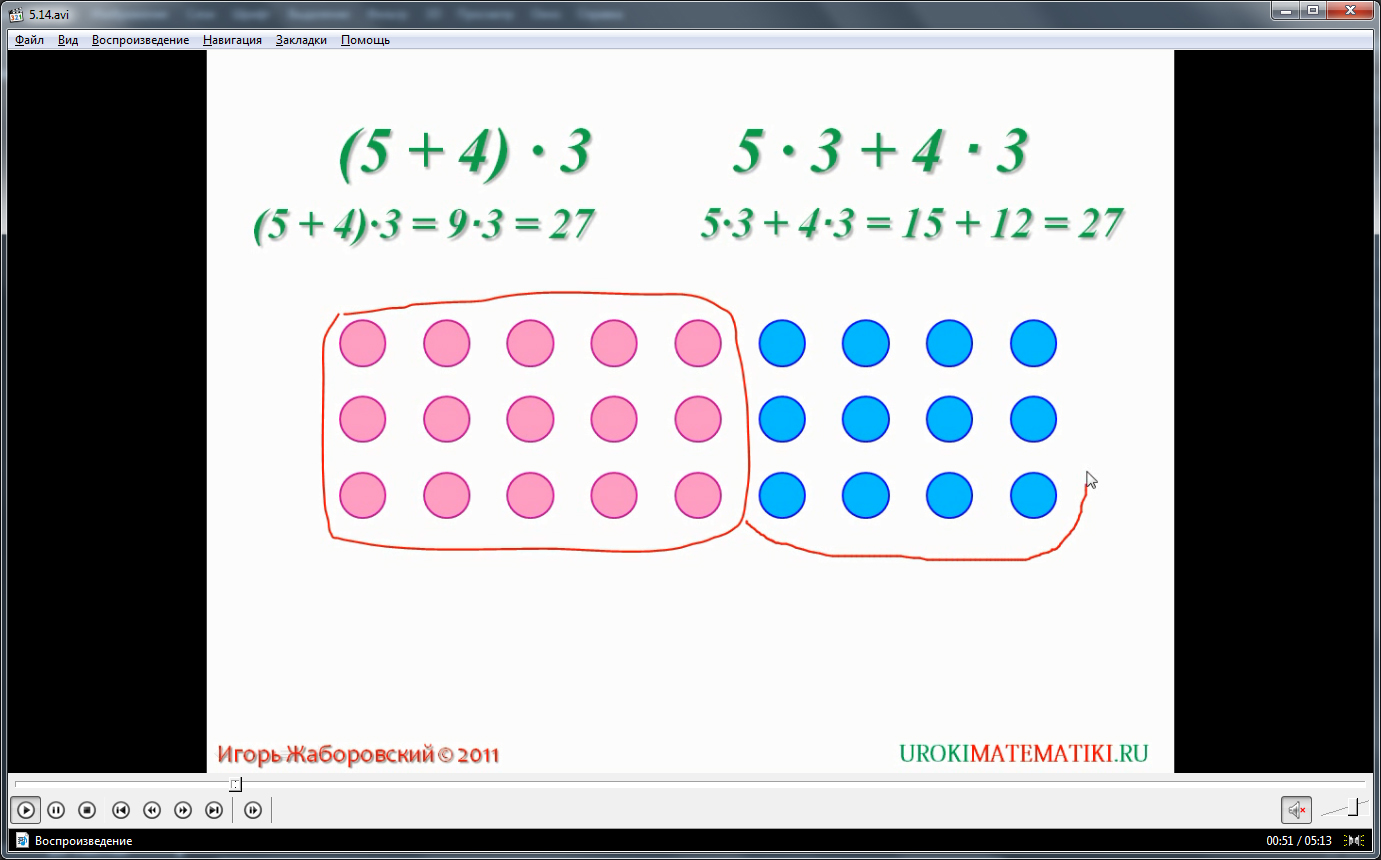
Видеоурок начинается с представление его темы. На экране отображается два выражения (5+4)·3 и 5·3+4·3. Отмечается, что два данных выражения имеют одинаковые ответы. Ниже раскрывается решение данных выражений. Отмечается, что в первом примере при решении выражения в скобках получается 9, которое при умножении на 3 дает 27. Аналогично во втором примере, следуем правилам выполнения операций. При умножении 5 на 3 получается 15, а при умножении 4·3 получается 12. Сложив между собой 12 и15, также можно получить 27.

Объяснение равенства выражений выполняется с помощью рисунка. На экране изображены 27 кружков, при этом 5 столбцов в три ряда – розовые кружки и 4 столбца в три ряда – голубые кружки. Для подсчета общего количества кружков можно выделить количество столбцов розовых кружков – 5 и количество столбцов голубых кружков – 4, а с учетом того, что для обоих цветов одинаковое число рядов – 3, составить выражения поиска решения (5+4)·3. Если же подсчитывать количество кружков отдельно для каждого цвета, а затем сложить вместе, то получим сумму произведения 5·3 с произведением 4·3.

Рассмотренный пример обобщается в общем правиле – чтобы перемножить число с некоторой суммой, необходимо умножить на него каждое слагаемое суммы, а после эти произведения сложить. Отмечается, что данное правило представляет распределительное свойство операции умножения. Формулировка правила, название свойства выделены цветным шрифтом и могут быть рекомендованы учителем к запоминанию. Далее следует буквенное обозначение распределительного свойства (a+b)c=ac+bc.

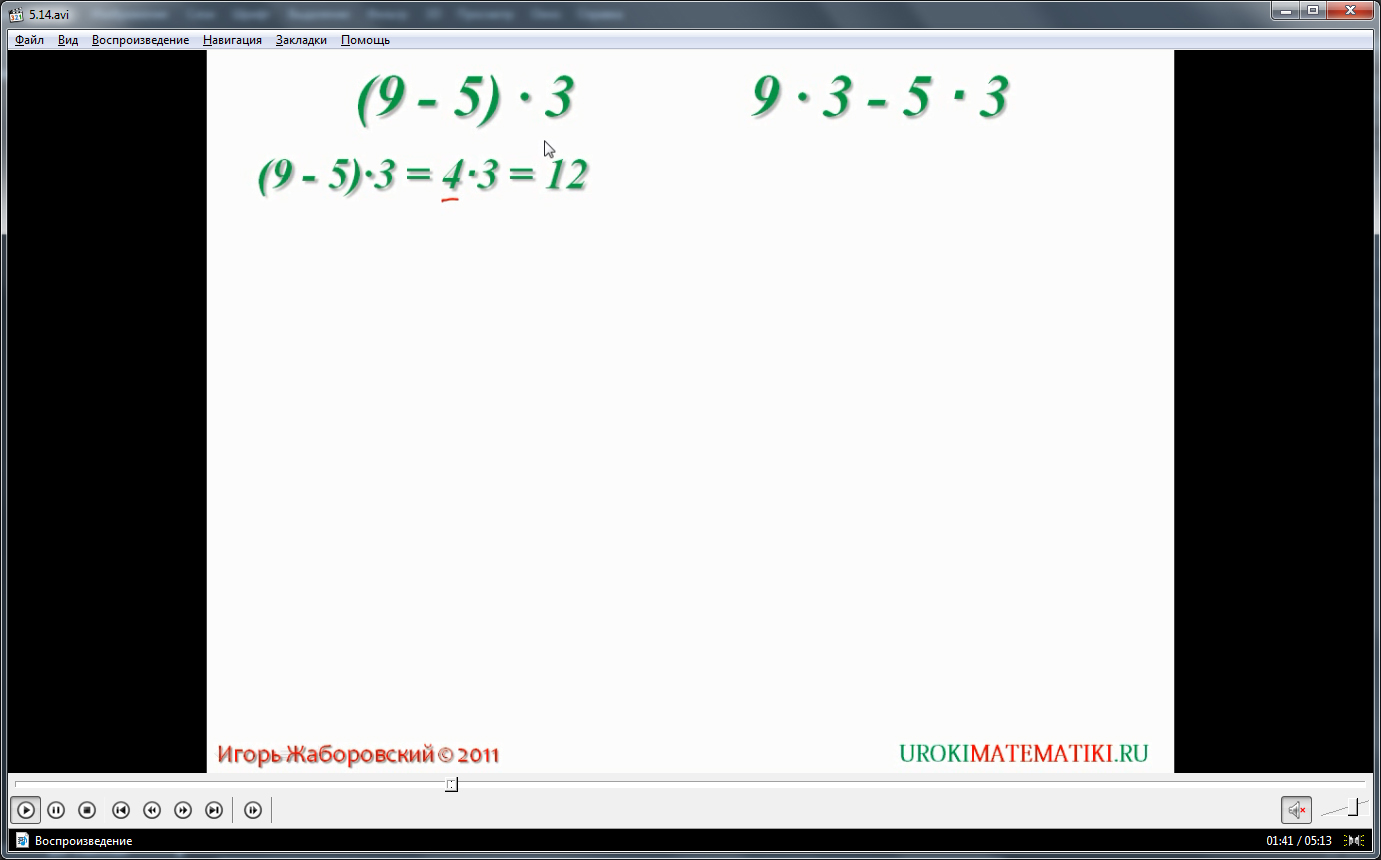
Далее представляется распределительное свойство, когда выражение в скобках представляет собой разность. Сравниваются решение выражения (9-5)·3 с решением 9·3-5·3. Отмечается, что данные выражения также имеют одинаковые значения. При вычислении разности в скобках 9-5 получается 4, то при умножении его на 3 получается 12. Аналогично при решении второго выражения получаем из первого произведения 9·3 значение 27, а из второго произведения получаем 15. Значение в результате вычитания из 27 числа 15 получаем 12. Таким образом, значения выражений равны. Отмечается, что данный пример является подтверждением распределительного свойства операции умножения, выполняемого относительно вычитания. Само свойство в общем виде указано в текстовом виде ниже примера. Сообщается, что для умножения разности чисел на третье число необходимо умножить на него уменьшаемое, а также вычитаемое, после этого от первого найденного произведения следует отнять второе произведение. Название правила выделено цветным шрифтом. Ниже текстового представления свойства дается буквенное его представление.

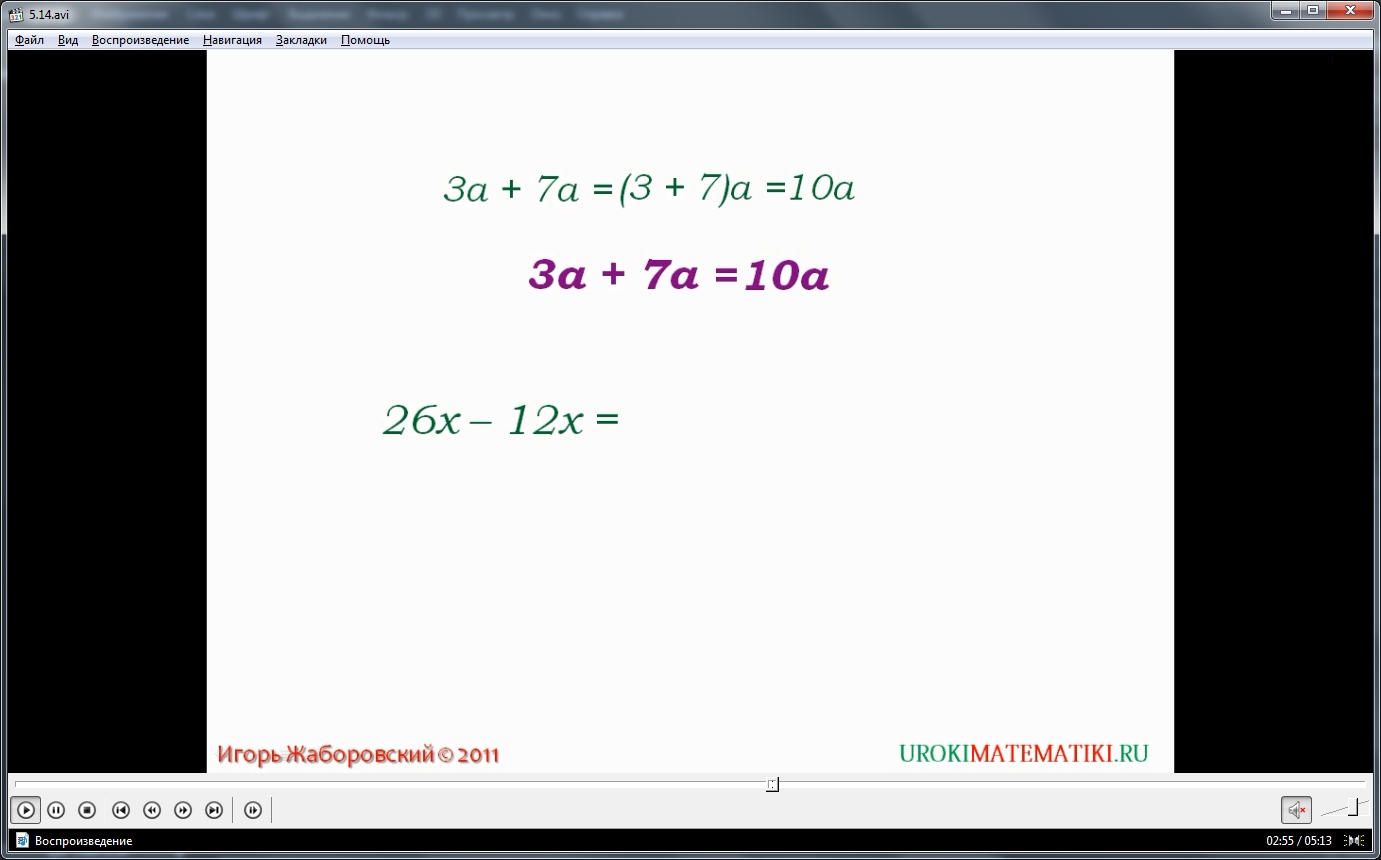
Отмечается, что рассмотренные свойства помогают в упрощении выражений. Представляются примеры, которые можно упростить помощью данного свойства. Используя данное свойство, упрощается 3а+7а. Так как выражение представляет собой сумму произведений, в каждом из которых есть множитель а, сначала в скобки заносится сумма числовых коэффициентов (3+7), а затем это выражение умножается на а. Выражение в скобках можно вычислить, в результате чего получается выражение 10а. Указывается краткая запись вычисления. Оговаривается, что обычно опускается вынесение общего множителя за скобки, записывая 3а+7а=10а. Чтобы объяснить, как получается данное выражение, дается наглядный образ – вместо х предлагается представить конфету. Таким образом, складывая 3 конфеты и 7 конфет, получается 10 конфет.

Таким же образом выполняется упрощение выражения 26х-12х. Сначала в скобки заносится выражение (26-12), а затем умножается на общий множитель х. в результате вычисления выражения в скобках, получаем значение выражения 14х. Так же, как и в предыдущем примере, оговаривается краткая запись упрощения 26х-12х=14х. пример также дополнен наглядным образом, предлагая представить вместо х конфеты. Таким образом, если вычесть из 26 конфет 12 конфет, то получится 14 конфет.

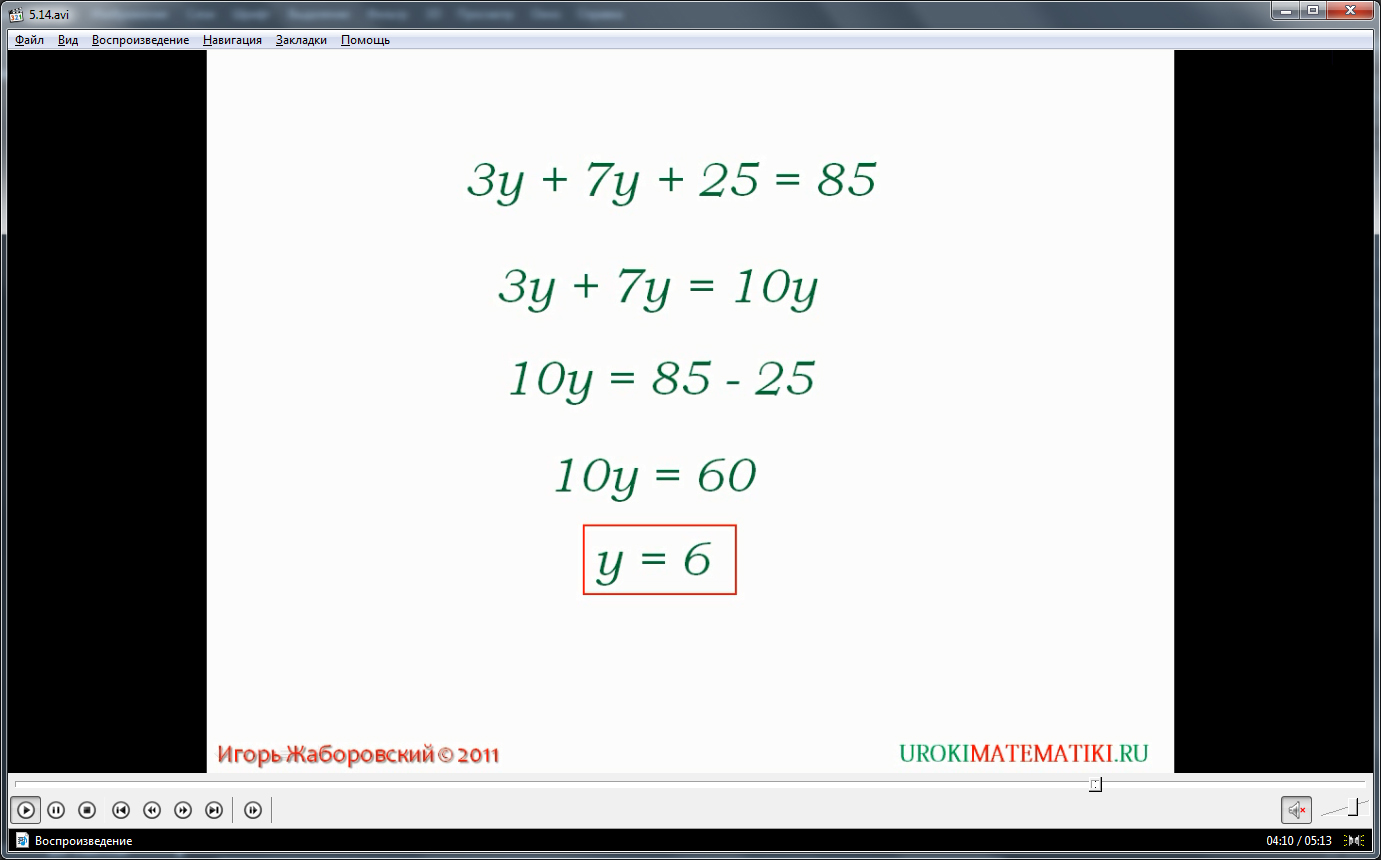
Далее предлагается рассмотреть решение уравнения 3у+7у+25=85. Учитывая возможность упростить уравнение, так как в нем есть выражение 3у+7у, то оно принимает вид 10у+25=85. Чтобы найти 10у, нужно из 85 вычесть 25. В результате получаем упрощенное уравнение 10у=60. Делением 60 на 10 получаем ответ у=6. Справедливость решения проверяем подстановкой 6 вместо у в исходное уравнение 3·6+7·6+25=85. Так как после вычисления выражения в левой части получаем число 85, уравнение решили верно.

Далее рассматривается сочетательное свойство умножения. Предлагается рассмотреть пример 2у·7·10. Чтобы решить данный пример, можно перераспределить множители так, чтобы у остался за скобками (2·7·10)у. после вычисления выражения в скобках, получаем 140у.

В конце видеоурока предлагается ответить на вопросы для проверки, насколько усвоен учебный материал. На первый вопрос необходимо ответить, как формулируется распределительное свойство операции умножения, выполняемого относительно вычитания, сложения. Во втором вопросе следует пояснить с помощью изученных правил упрощение выражений.

Видеоурок «Упрощение выражений» используется на традиционном школьном уроке математики для повышения его эффективности. Также он может использоваться учителем, осуществляющим дистанционное обучение, в качестве наглядного пособия. Материал может быть рекомендован ученикам, которым необходимо дополнительное занятие для усвоения материала, или требуется самостоятельное изучение на дому.

Источник

Как упростить алгебраическое выражение

Некоторые алгебраические примеры одним видом способны наводить ужас на школьников. Длинные выражения не только пугают, но и очень затрудняют вычисления. Пытаясь сходу понять, что и за чем следует, недолго запутаться. Именно по этой причине математики всегда стараются максимально упростить «жуткое» задание и только потом приступают к его решению. Как ни странно, такой трюк значительно ускоряет процесс работы.

Упрощение является одним из фундаментальных моментов в алгебре. Если в простых задачах без него ещё можно обойтись, то более трудные для вычисления примеры могут оказаться «не по зубам». Тут-то и пригодятся эти навыки! Тем более что сложных математических знаний не требуется: достаточно будет всего лишь запомнить и научиться применять на практике несколько базовых приёмов и формул.

Необходимые знания и умения

Вне зависимости от сложности вычислений при решении любого выражения важно соблюдать порядок выполнения операций с числами:

Последние два пункта можно спокойно поменять местами и это никак не отразится на результате. Но складывать два соседних числа, когда рядом с одним из них стоит знак умножения категорически нельзя! Ответ если и получится, то неверный. Поэтому нужно запомнить последовательность.

Применение подобных

К таким элементам относятся числа с переменной одного порядка или одинаковой степени. Существуют и так называемые свободные члены, не имеющие рядом с собой буквенного обозначения неизвестного.

Суть заключается в том, что при отсутствии скобок можно упростить выражение, складывая или вычитая между собой подобные.

Несколько наглядных примеров:

Разложение числа на множители

Эта маленькая математическая хитрость, если научиться её правильно использовать, в будущем не раз поможет справиться с каверзной задачкой. Да и понять, как работает «система», несложно: разложением называют произведение нескольких элементов, вычисление которого даёт исходное значение. Таким образом, 20 можно представить как на 20×1, 2×10, 5×4, 2×5×2 или другим способом.

На заметку: множители всегда совпадают с делителями. Так что искать рабочую «пару» для разложения нужно среди чисел, на которые исходное делится без остатка.

Проделывать такую операцию можно как со свободными членами, так и с цифрами при переменной. Главное, не потерять последнюю во время вычислений — даже после разложения неизвестная не может взять и «уйти в никуда». Она остаётся при одном из множителей:

Простые числа, которые можно разделить лишь на себя или 1, никогда не раскладываются — в этом нет смысла.

Основные способы упрощения

Первое, за что цепляется взгляд:

Алгебраические примеры в школьной программе часто составляются с учётом того, что их можно красиво упростить.

Вычисления в скобках

Внимательно следите за знаком, стоящим перед скобками! Умножение или деление применяется к каждому элементу внутри, а минус — меняет имеющиеся знаки «+» или «-» на противоположные.

Скобки вычисляются по правилам либо по формулам сокращённого умножения, после чего приводятся подобные.

Сокращение дробей

Сокращать дроби тоже несложно. Они сами через раз «охотно убегают», стоит произвести операции с приведением подобных членов. Но упростить пример можно ещё до этого: обращайте внимание на числитель и знаменатель. Они нередко содержат явные или скрытые элементы, которые можно взаимно сократить. Правда, если в первом случае нужно всего лишь вычеркнуть лишнее, во втором придётся подумать, приводя часть выражения к виду для упрощения. Используемые методы:

Когда выражение или его часть находится под корнем, первостепенная задача упрощения практически аналогична случаю с дробями. Необходимо искать способы полностью от него избавиться или, если это невозможно, максимально сократить мешающий вычислениям знак. Например, до ненавязчивого √(3) или √(7).

Верный способ упростить подкоренное выражение — попытаться разложить его на множители, часть из которых выносится за пределы знака. Наглядный пример: √(90)=√(9×10) =√(9)×√(10)=3√(10).

Другие маленькие хитрости и нюансы:

Упрощение степенного выражения

Если в случае простых вычислений на минус или плюс примеры упрощаются за счёт приведения подобных, то как быть при умножении или делении переменных с разными степенями? Их можно легко упростить, запомнив два основных момента:

Единственное условие для такого упрощения — одинаковое основание у обоих членов. Примеры для наглядности:

Отмечаем, что операции с числовыми значениями, стоящими перед переменными, происходят по обычным математическим правилам. И если присмотреться, то становится понятно, что степенные элементы выражения «работают» аналогично:

Как и в любом деле, при упрощении алгебраических выражений необходимо не только знание основ, но и практика. Уже через несколько занятий примеры, когда-то кажущиеся сложными, будут сокращаться без особого труда, превращаясь в короткие и легко решаемые.

Видео

Это видео поможет вам разобраться и запомнить, как упрощаются выражения.

Источник

Упрощения алгебраических выражений

Что значит упростить алгебраическое выражение

Алгебраическое выражение — одна или несколько алгебраических величин (чисел и переменных), которые объединены с помощью знаков арифметических действий в виде сложения, вычитания, умножения, деления, извлечения корня, возведения в степень (при целых значениях показателей корня и степени), знаков последовательности, определяющих порядок применения данных операций (скобки разного вида).

Обязательным условием для алгебраического выражения является конечное число величин, которые его составляют. Данный принцип пригодиться математикам для решения задач в средних классах школы.

Упростить выражение — это значит уменьшить число арифметических действий, необходимых для вычисления значения данного выражения с учетом определенных значений переменных.

Правила упрощения алгебраических выражений

Существуют основные методы в алгебре для того, чтобы упростить алгебраическое выражение:

В процессе приведения выражения в более простую форму следует использовать полезные советы:

Приведение подобных

Приведение подобных слагаемых в теории заключается в сложении их коэффициентов и приписывании буквенной части.

Подобными являются слагаемые (одночлены), которые обладают буквенной частью.

В выражении 2ab+3ab+b одночлены 2ab и 3ab являются подобными слагаемыми.

Привести подобные — значит, выполнить сложение нескольких подобных слагаемых для получения в результате одного слагаемого.

К примеру, приведем слагаемые:

Заметим, что числа в таких слагаемых умножают на буквы. Данные числа носят названия коэффициентов.

Рассмотрим выражение с квадратной степенью:

Здесь число 3 является коэффициентом.

Разложение на множители

Разложить выражение на множители можно, если вынести общий множитель за скобки, применить формулы сокращенного умножения и другие.

a b 2 + a 2 c = a b 2 + a c

В распространенных случаях разложение на множители следует за приведением подобных при упрощении выражений. В итоге получаются произведения. Чтобы это понять, отдельно нужно упомянуть правила действия с дробями, а именно, при сокращении дроби числитель и знаменатель требуется записать, как произведения.

Сокращение дроби

В процессе сокращения дроби допустимо выполнять умножение или деление числителя и знаменателя дроби на одинаковое число, отличное от нуля, в результате чего величина дроби остается прежней.

Объяснение алгоритм действий при сокращении дробей:

a a + b a 2 = a a + b a · a = a + b a

Важно заметить, что сокращению подлежат исключительно множители.

Озвученное правило является следствием ключевого свойства дроби. Оно состоит в допустимости умножения или деления числителя и знаменателя дроби на одно и то же число, которое не равно нулю. В результате значение дроби останется без изменений.

Существует простой способ, руководствуясь которым можно определить, разложено ли выражение на множители. Арифметическое действие, выполняемое в последнюю очередь при вычислении значения выражения, считается «главным».

Данное правило состоит в том, что, когда при подстановке каких-либо чисел на замену буквам и вычислении значения выражения последнее действие представляет собой умножение, можно заключить, что перед нами произведение, то есть выражение разложено на множители. В том случае, когда на последнем шаге в процессе расчетов выполняется сложение или вычитание, разложение выражения на множители не выполнено, то есть сокращение не допускается.

Сложение и вычитание дробей

При сложении и вычитании обыкновенных дробей требуется найти общий знаменатель, умножить каждую из дробей на недостающий множитель и сложить или вычесть числители:

a b + c d = a · d + c · b b · d ;

Разберем правило на конкретных примерах. Вычислим:

Заметим, что знаменатели являются взаимно простыми, то есть не имеют общих множителей. Таким образом, наименьший общий множитель данных чисел соответствует их произведению. В результате:

В данном случае общим множителем является число 24. Выполним преобразования и упростим выражение:

В данном примере следует смешанные дроби записать в виде неправильных. Далее можно упростить выражение по стандартному алгоритму:

Разберем самостоятельный случай, когда знаменатели не содержат буквы. При этом алгоритм действий такой же, как и при действиях с обыкновенными дробями:

Здесь общий множитель равен 12. Тогда:

a 2 b · 3 4 + a · 2 6 = 3 a 2 b + 2 a 12

Далее можно привести подобные в числители, и разложить на множители при их наличии:

a 2 b 4 + a 6 = 3 a 2 b + 2 a 12 = a 3 a b + 2 12

Когда знаменатели содержат буквы, схема действий существенно не меняется:

Рассмотрим пример, когда требуется упростить выражение:

Разложим знаменатели на множители:

a b 2 = a · b · b a 2 b = a · a · b

Вычислим единые множители:

a b 2 = a ¯ · b ¯ ¯ · b a 2 b = a ¯ · a · b ¯ ¯

Затем можно записать общие множители и выполнить умножение:

a ¯ · b ¯ ¯ · a · b = a 2 b 2

1 a b 2 · a + 1 a 2 b · b = a + b a 2 b 2

Умножение и деление дробей

Умножение и деление дробей выполняют таким образом:

a b · c d = a · c b · d ;

a b : c d = a · d b · c

Арифметические действия выполняют в следующем порядке:

Важно заметить, что при наличии скобок, операции, которые в них заключены, необходимо выполнить в первую очередь. Далее можно приступать к раскрытию скобок. Когда имеется несколько скобок с арифметическими действиями, которые нужно умножить или разделить, в начале проводят вычисления в каждой из скобок, а затем умножение или деление полученных результатов. При наличии внутренних скобок, заключенных в скобки, действия в них выполняют в первую очередь.

Используя правило умножения и деления дробей, получим:

Во многих примерах имеются не только цифры, но и буквы. В этом случае выполняются алгебраические действия, в том числе, приведение подобных, сложение, сокращение дробей и другие операции. Отличия можно заметить при разложении многочленов на множители. Для этого следует пользоваться формулами сокращенного умножения или вынесением единого множителя за скобки.

Ключевой задачей при работе с такими выражениями является запись выражений в виде произведения или частного.

Попробуем упростить выражение:

Так как имеются скобки, следует начать преобразования именно с них. Упростим разность дробей, которая в них записана, чтобы получить вместо нее произведение или частное. Приведем дроби к единому знаменателю и определим сумму:

Заметим, что дальнейшие преобразования не приведут к упрощению данного выражения. Причина этого заключается в том, что каждый из множителей является элементарным. В результате:

Пояснения на примерах

Требуется упростить выражения:

Приведем подобные и упростим выражения:

Заметим, что ab и 2ba являются подобными по той причине, что:

В результате можно сделать вывод, что данные слагаемые обладают одинаковой буквенной частью.

Требуется упростить выражения:

Путем разложения на множители упростим данные выражения:

a b 2 + a 2 c = a b 2 + a c

72 30 = 2 · 2 · 2 · 3 · 3 2 · 3 · 5 = 2 · 2 · 2 · 3 · 3 2 · 3 · 5 = 2 · 2 · 3 5 = 12 5

a a + b a 2 = a a + b a · a = a + b a

В первую очередь выполним разложение на множители:

Дано выражение, которое требуется упростить:

В данном случае требуется разложить знаменатели на множители. Первый знаменатель записан так, что можно вынести за скобки х. Второй знаменатель содержит разность квадратов. Выполним преобразования:

Рассмотрим выражение на наличие общих множителей:

Заметим, что при переносе слагаемых, заключенных в скобках, изменился знак перед дробью. Приведем выражения к единому знаменателю:

Воспользуемся формулой сокращенного умножения, а именно, разностью кубов:

Заметим, что в знаменателе дроби расположено выражение, которое называют неполным квадратом суммы:

x 2 + 2 x + 4 = x 2 + 2 · x + 2 2

Второе по счету слагаемое в неполном квадрате суммы является произведением первого и последнего. Неполный квадрат суммы представляет собой множитель, который входит в состав разложения разности кубов:

Требуется упростить выражения:

Дано выражение, которое требуется упростить:

При наличии в знаменателях одного и того же множителя, возведенного в разные степени, то в общем знаменателе данный множитель будет обладать самой большой из имеющихся степеней. Применительно к этой задаче, общий знаменатель будет состоять из следующих выражений:

a во второй степени;

x в третьей степени;

b в третьей степени;

y в четвертой степени.

В результате получим:

Нужно упростить выражение:

Исключить ошибки можно, если расписать заранее порядок операций. В первую очередь целесообразно суммировать дроби, расположенные в скобках. В результате будет получена только одна дробь. Далее можно приступить к делению дробей. Полученный итог следует прибавить к последней дроби.

Выглядит этот алгоритм таким образом:

Источник