Как упрощать выражения тригонометрия

Упрощение тригонометрических выражений. Задание 9

Упрощение тригонометрических выражений. Задание 9.

При упрощении тригонометрических выражений полезно придерживаться такой последовательности действий:

1. С помощью формул приведения привести все тригонометрические функции к углам первой четверти.

2. Посмотреть, как соотносятся между собой полученные углы, чтобы определить, какие формулы использовать для преобразования выражения. В большинстве задач это формулы двойного аргумента или соотношение

Прежде чем читать дальше, очень рекомендую перечитать статью, как пользоваться формулами приведения и не заучивать их.

Рассмотрим несколько примеров решения задач на упрощение тригонометрических выражений из Открытого банка заданий для подготовки к ЕГЭ по математике.

Мы видим, что , поэтому либо разложим знаменатель по формуле косинуса двойного аргумента, либо, наоброт свернем числитель по той же формуле:

Заметим, что

Воспользеумся фомулой приведения:

Ответ: 5.

Преобразуем аргументы тригонометрических функций в знаменателе дроби:

С помощью тригонометрического круга определим значение

и :

Получим:

Воспользуемся формулой приведения:

Снова воспользуемся формулой приведения:

Ответ: 12.

По основному тригонометрическому тождеству:

Косинус в третьей четверти отрицателен, поэтому

Отсюда

Ответ: 5.

Источник

Урок «Упрощение тригонометрических выражений»

Краткое описание документа:

Видеоурок «Упрощение тригонометрических выражений» предназначен для формирования навыков у учеников в решении тригонометрических задач с использованием основных тригонометрических тождеств. В ходе видеоурока рассматриваются виды тригонометрических тождеств, примеры решения задач с их использованием. Применяя наглядное пособие, учителю легче достичь целей урока. Яркое представление материала способствует запоминанию важных моментов. Использование анимационных эффектов и озвучивание позволяют полностью заменить учителя на этапе объяснения материала. Таким образом, применяя данное наглядное пособие на уроках математики, учитель может повысить эффективность обучения.

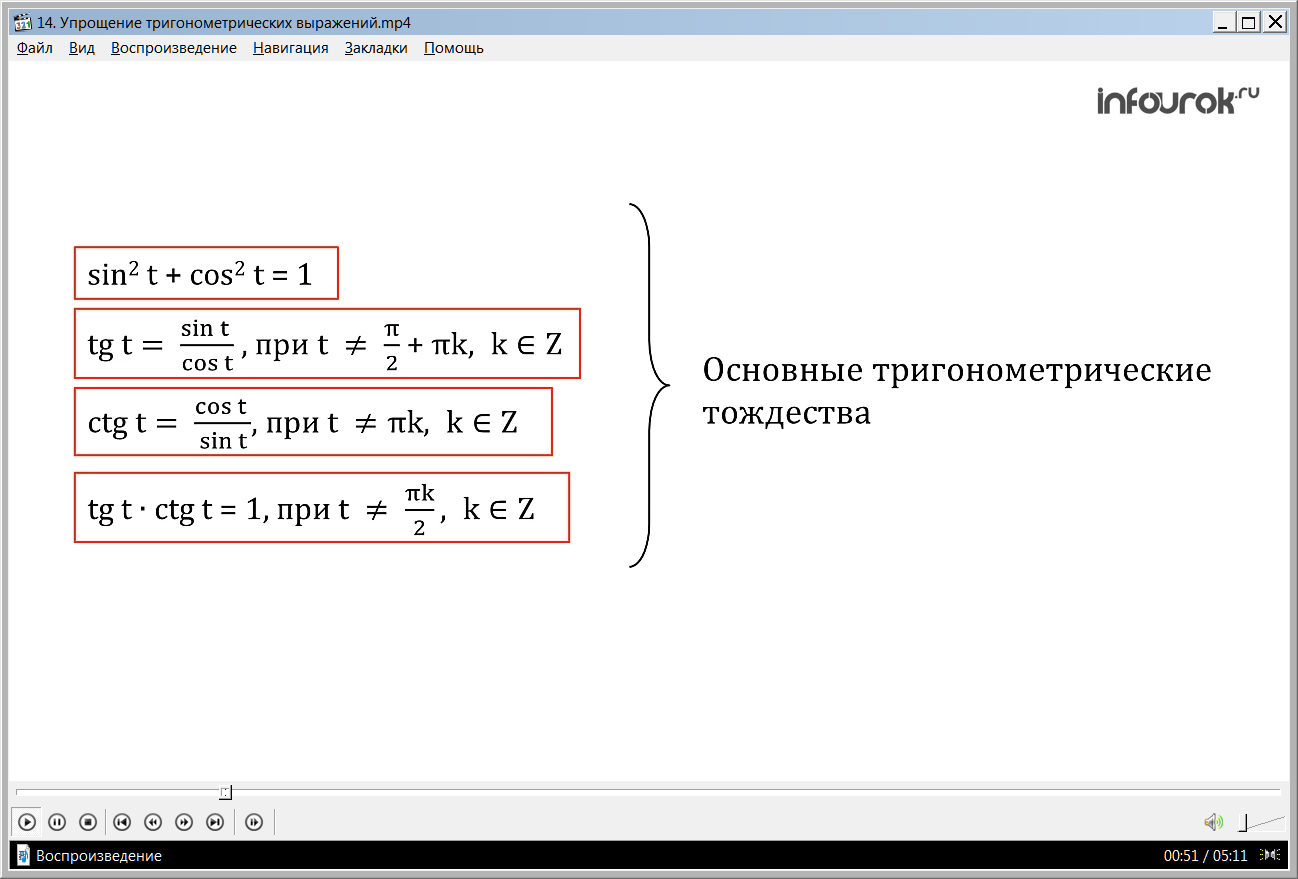
В начале видеоурока объявляется его тема. Затем напоминаются тригонометрические тождества, изученные ранее. На экране отображаются равенства sin 2 t+cos 2 t=1, tg t=sin t/cos t, где t≠π/2+πk для kϵZ, ctg t=cos t/sin t, верное для t≠πk, где kϵZ, tg t· ctg t=1, при t≠πk/2, где kϵZ, названные основными тригонометрическими тождествами. Отмечается, что данные тождества часто применяются в решении задач, где необходимо доказать равенство или упростить выражение.

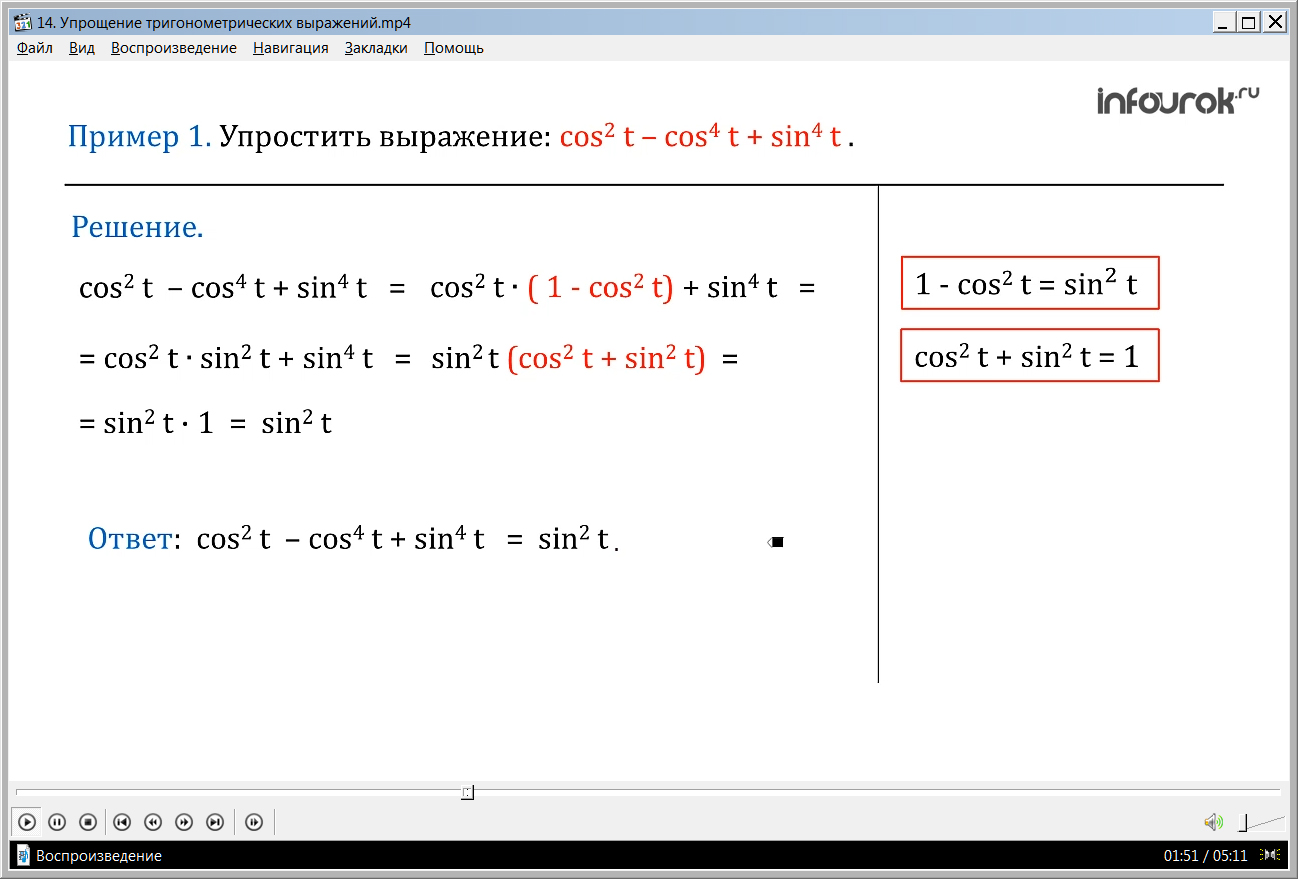
Дальее рассматриваются примеры применения данных тождеств в решении задач. Сначала предлагается рассмотреть решение задач по упрощению выражений. В примере 1 необходимо упростить выражение cos 2 t- cos 4 t+ sin 4 t. Чтобы решить пример, сначала выносится за скобки общий множитель cos 2 t. В результате такого преобразования в скобках получается выражение 1- cos 2 t, значение которого из основного тождества тригонометрии равно sin 2 t. После преобразования выражения очевидна возможность выведения за скобки еще одного общего множителя sin 2 t, после чего выражение приобретает вид sin 2 t(sin 2 t+cos 2 t). Из того же основного тождества выводим значение выражения в скобках, равное 1. В результате упрощения получаем cos 2 t- cos 4 t+ sin 4 t= sin 2 t.

В примере 2 также выражение cost/(1- sint)+ cost/(1+ sint) нужно упростить. Так как в числителях обеих дробей находится выражение cost, его можно вывести за скобки как общий множитель. Затем дроби в скобках приводятся к общему знаменателю перемножением (1- sint)(1+ sint). После приведения подобных слагаемых в числителе остается 2, а в знаменателе 1- sin 2 t. В правой части экрана напоминается основное тригонометрическое тождество sin 2 t+cos 2 t=1. Используя его, находим знаменатель дроби cos 2 t. После сокращения дроби получим упрощенный вид выражения cost/(1- sint)+ cost/(1+ sint)=2/cost.

Видеоурок «Упрощение тригонометрических выражений» рекомендуется применять на традиционном школьном уроке математики. Также материал будет полезен учителю, осуществляющему дистанционное обучение. С целью формирования навыка в решении тригонометрических задач.

«Упрощение тригонометрических выражений».

1)sin 2 t + cos 2 t = 1( синус квадрат тэ плюс косинус квадрат тэ равно одному)

2)tgt =, при t ≠ + πk, kϵZ( тангенс тэ равно отношению синуса тэ к косинусу тэ при тэ не равном пи на два плюс пи ка, ка принадлежит зэт)

называют основными тригонометрическими тождествами.

Часто они используются при упрощении и доказательстве тригонометрических выражений.

Рассмотрим примеры использования этих формул при упрощении тригонометрических выражений.

( вынесем за скобку общий множитель косинус квадрат тэ, в скобках получим разность единицы и квадрата косинуса тэ, что равно по первому тождеству квадрату синуса тэ. Получим сумму синус четвертой степени тэ произведения косинус квадрат тэ и синус квадрат тэ. общий множитель синус квадрат тэ вынесем за скобки, в скобках получим сумму квадратов косинуса и синуса, что по основному тригонометрическому тождеству равно единице. В итоге получим квадрат синуса тэ).

( Вынесем общий множитель косинус тэ за скобки, а в скобках приведем к общему знаменателю, который представляет собой произведение один минус синус тэ на один плюс синус тэ.

В числителе получим: единица плюс синус тэ плюс единица минус синус тэ, приводим подобные, числитель равен двум после приведения подобных.

В знаменателе можно применить формулу сокращенного умножения (разность квадратов) и получить разность единицы и квадрата синуса тэ, что по основному тригонометрическому тождеству

равно квадрату косинуса тэ. После сокращения на косинус тэ получим конечный ответ : два деленное на косинус тэ).

Рассмотрим примеры использования этих формул при доказательстве тригонометрических выражений.

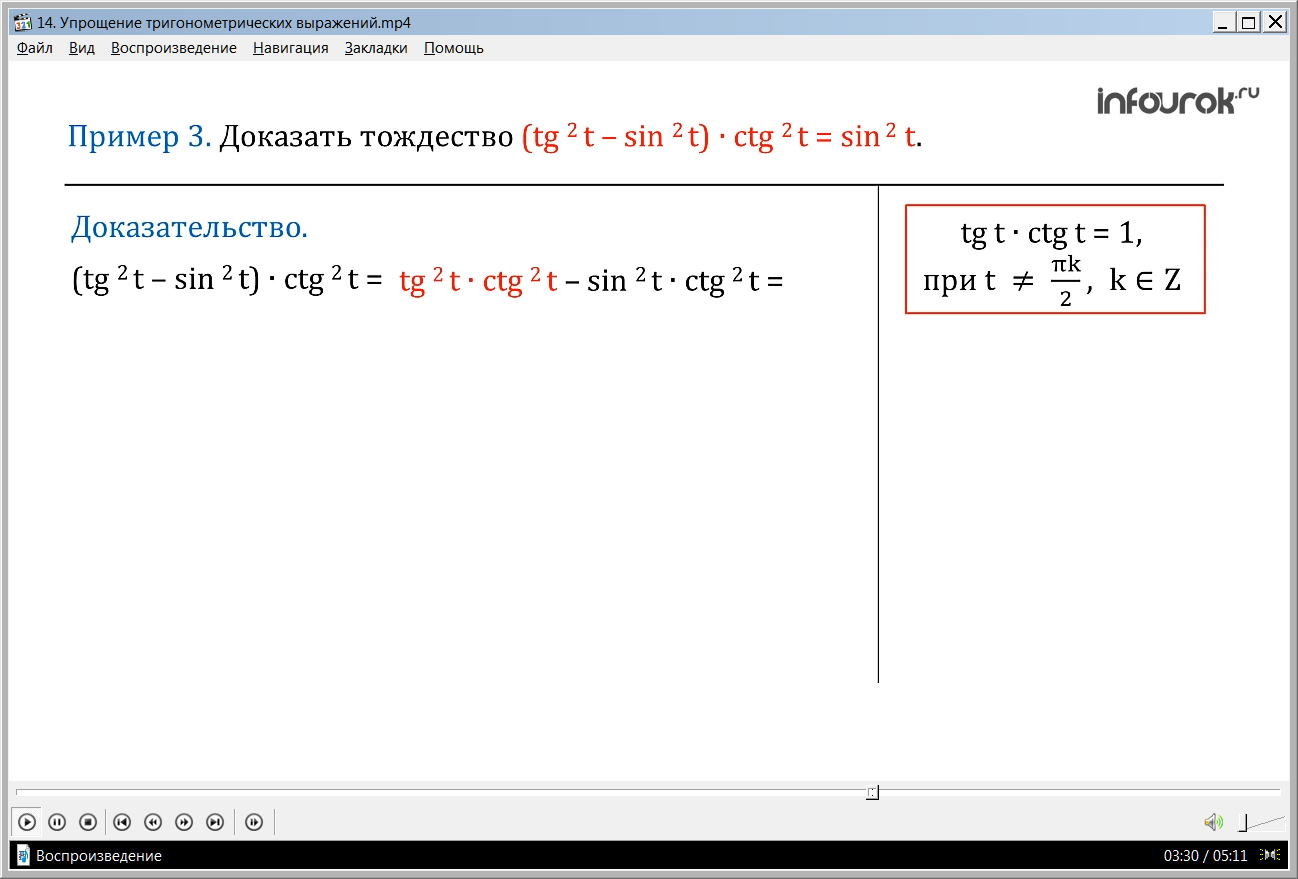
ПРИМЕР 3. Доказать тождество (tg 2 t – sin 2 t) ∙ ctg 2 t = sin 2 t (произведение разности квадратов тангенса тэ и синуса тэ на квадрат котангенса тэ равно квадрату синуса тэ).

Преобразуем левую часть равенства:

( Раскроем скобки, из ранее полученного соотношения известно, что произведение квадратов тангенса тэ на котангенс тэ равно единице. Вспомним, что котангенс тэ равен отношению косинуса тэ на синус тэ, значит, квадрат котангенса это отношение квадрата косинуса тэ на квадрат синуса тэ.

После сокращения на синус квадрат тэ получим разность единицы и косинуса квадрата тэ, что равно синусу квадрату тэ). Что и требовалось доказать.

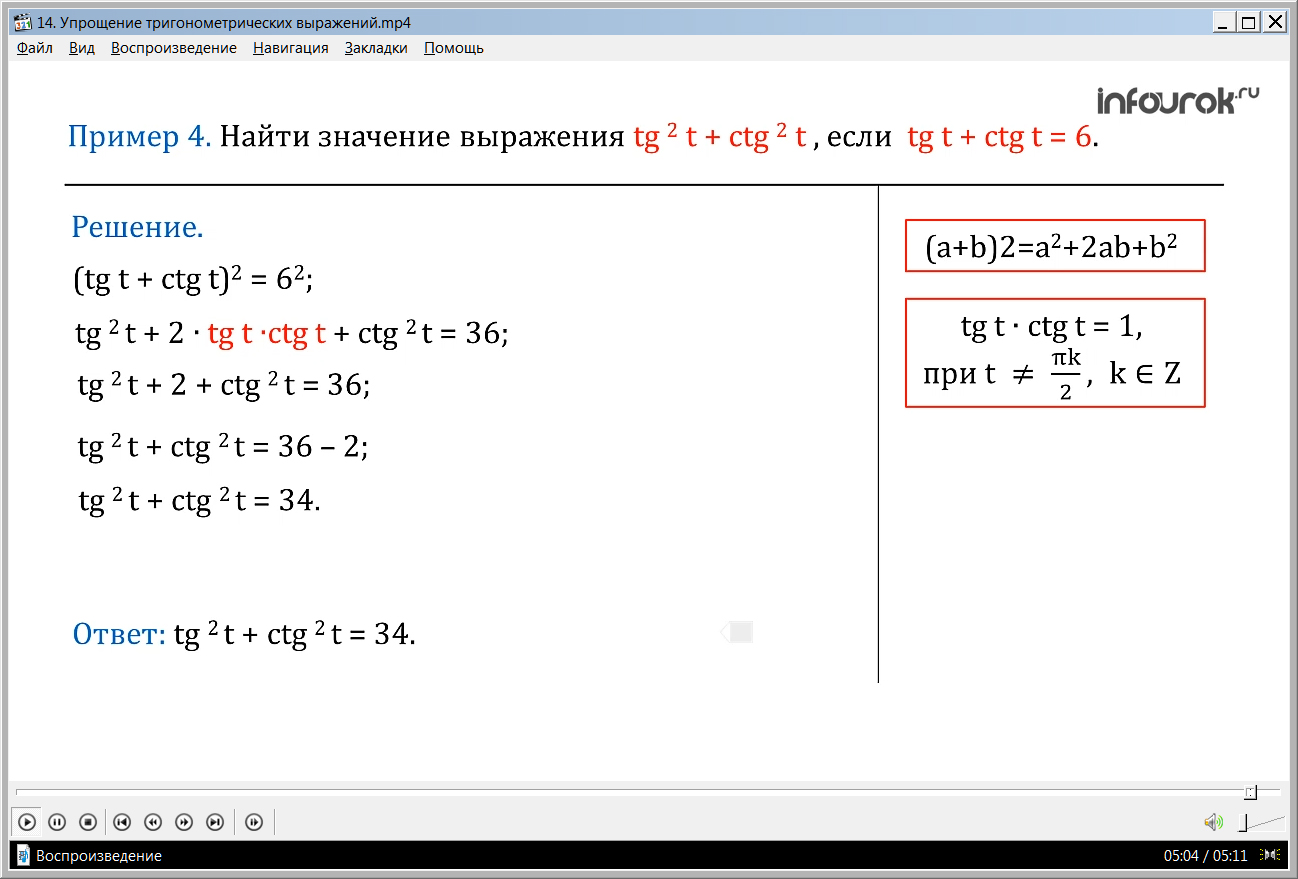
( сумма квадратов тангенса тэ и котангенса тэ, если сумма тангенса и котангенса равна шести).

Решение. (tgt + ctgt) 2 = 6 2

tg 2 t + 2 ∙ tgt ∙ctgt + ctg 2 t = 36

tg 2 t + 2 + ctg 2 t = 36

tg 2 t + ctg 2 t = 36-2

tg 2 t + ctg 2 t = 34

Возведем обе части исходного равенства в квадрат:

(tgt + ctgt) 2 = 6 2 ( квадрат суммы тангенса тэ и котангенса тэ равна шести в квадрате). Вспомним формулу сокращённого умножения: Квадрат суммы двух величин равен квадрату первой плюс удвоенное произведение первой на вторую плюс квадрат второй. (a+b) 2 =a 2 +2ab+b 2 Получим tg 2 t + 2 ∙ tgt ∙ctgt + ctg 2 t = 36 (тангенс квадрат тэ плюс удвоенное произведение тангенса тэ на котангенс тэ плюс котангенс квадрат тэ равно тридцати шести).

Так как произведение тангенса тэ на котангенс тэ равно единице, то tg 2 t + 2 + ctg 2 t = 36 ( сумма квадратов тангенса тэ и котангенса тэ и двух равна тридцати шести),

значит tg 2 t + ctg 2 t = 34 (сумма квадратов тангенса тэ и котангенса тэ равна тридцати четырем). Ответ: 34.

Источник

Упрощение тригонометрических выражений. Решение тригонометрических уравнений различными методами (подготовка к ЕГЭ). 11-й класс

Разделы: Математика

Класс: 11

Занятие 1

Тема: 11 класс (подготовка к ЕГЭ)

Упрощение тригонометрических выражений.

Решение простейших тригонометрических уравнений. (2 часа)

Цели:

Оборудование к уроку: КРМу, ноутбуки на каждого ученика.

Структура урока:

1. Оргмомент. (2 мин.)

Учитель приветствует аудиторию, объявляет тему урока, напоминает о том, что ранее было дано задание повторить формулы тригонометрии и настраивает учащихся на тестирование.

2. Тестирование. (15мин + 3мин. обсуждение)

Вариантов может быть сколько угодно, приведу пример одного их них:

I вариант.

а) основные тригонометрические тождества

1. sin 2 3y + cos 2 3y + 1;

б) формулы сложения

в) преобразование произведения в сумму

г) формулы двойных углов

д) формулы половинных углов

е) формулы тройных углов

ж) универсальная подстановка

з) понижение степени

Учащиеся на ноутбуке напротив каждой формулы видят свои ответы.

Работу мгновенно проверяет компьютер. Результаты высвечиваются на большом экране ко всеобщему обозрению.

Также после окончания работы показываются на ноутбуках учащихся правильные ответы. Каждый ученик видит, где сделана ошибка, и какие формулы ему нужно повторить.

3. Упрощение тригонометрических выражений. (25 мин.)

Цель – повторить, отработать и закрепить применение основных формул тригонометрии. Решение задач В7 из ЕГЭ.

На данном этапе класс целесообразно разбить на группы сильных (работают самостоятельно с последующей проверкой) и слабых учеников, которые работают с учителем.

Задание для сильных учащихся (заранее подготовлены на печатной основе). Основной упор сделан на формулы приведения и двойного угла, согласно ЕГЭ 2011.

Упростить выражения (для сильных учащихся):

Параллельно учитель работает со слабыми учащимися, обсуждая и решая под диктовку учеников задания на экране.

Наступила очередь обсуждения результатов работы сильной группы.

На экране появляются ответы, а также, с помощью видеокамеры выводятся работы 5-ти разных учеников (по одному заданию у каждого).

Слабая группа видит условие и метод решения. Идет обсуждение и анализ. С использованием технических средств это происходит быстро.

4. Решение простейших тригонометрических уравнений. (30 мин.)

Цель – повторить, систематизировать и обобщить решение простейших тригонометрических уравнений, запись их корней. Решение задачи В3.

Любое тригонометрическое уравнение, каким бы способом мы его не решали, приводит к простейшему.

При выполнении задания следует обращать внимание учащихся на запись корней уравнений частных случаев и общего вида и на отбор корней в последнем уравнении.

В ответ записать наименьший положительный корень.

5. Самостоятельная работа (10 мин.)

Предлагается разноуравневая работа на выбор учащегося.

1) Найти значение выражения

3) Решить уравнение

1) Найти значение выражения

2) Решить уравнение В ответе записать наименьший положительный корень.

1) Найти tgα, если

2) Найти корень уравнения В ответ запишите наименьший положительный корень.

6. Итог урока (5 мин.)

Учитель подводит итоги о том, что на уроке повторили и закрепили тригонометрические формулы, решение простейших тригонометрических уравнений.

Задается домашнее задание (подготовленное на печатной основе заранее) с выборочной проверкой на следующем уроке.

9) В ответе указать наименьший положительный корень.

10) В ответе указать наименьший положительный корень.

Занятие 2

Тема: 11 класс (подготовка к ЕГЭ)

Методы решений тригонометрических уравнений. Отбор корней. (2 часа)

Цели:

Оборудование к уроку: КРМу, ноутбуки на каждого ученика.

Структура урока:

1. Оргмомент (2 мин.)

Учитель приветствует аудиторию, объявляет тему урока и план работы.

2. а) Разбор домашнего задания (5 мин.)

Цель – проверить выполнение. Одна работа с помощью видео камеры выдается на экран, остальные выборочно собираются на проверку учителя.

б) Разбор самостоятельной работы (3 мин.)

На экране ответы и решения, у учащихся заранее выданные их работы. Быстро идет анализ.

3. Повторение методов решения тригонометрических уравнений (5 мин.)

Цель – вспомнить методы решения тригонометрических уравнений.

Спросить у учащихся, какие методы решений тригонометрических уравнений они знают. Акцентировать на том, что есть так называемые основные (часто используемые) методы:

и есть прикладные методы:

Также нужно напомнить, что одно уравнение может решаться различными способами.

4. Решение тригонометрических уравнений (30 мин.)

Цель – обощить и закрепить знания и навыки по данной теме, подготовиться к решению С1 из ЕГЭ.

Считаю целесообразным прорешать вместе с учащимися уравнения на каждый метод.

Ученик диктует решение, учитель записывает на планшет, весь процесс отображается на экране. Это позволит быстро и эффективно восстановить в памяти ранее пройденный материал.

2) разложение на множители 3cos(x/3) + 4cos 2 (x/3) = 0

4) преобразование суммы в произведение cos5x + cos7x = cos(π + 6x)

5) преобразование произведения в сумму 2sinx sin2x + cos3x = 0

7) универсальная тригонометрическая подстановка sinx + 5cosx + 5 = 0.

Решая это уравнение, следует отметить, что использование данного метода ведет к сужению области определения, так как синус и косинус заменяется на tg(x/2). Поэтому, прежде чем выписывать ответ, нужно сделать проверку, являются ли числа из множества π + 2πn, n Z конями данного уравнения.

9) умножение на некоторую тригонометрическую функцию cosx cos2x cos4x = 1/8.

5. Отбор корней тригонометрических уравнений (20 мин.)

Так как в условиях жесткой конкуренции при поступлении в ВУЗы решение одной первой части экзамена недостаточно, то следует большинству учащихся обращать внимание на задания второй части (С1,С2,С3).

Поэтому цель этого этапа занятия – вспомнить ранее изученный материал, подготовиться к решению задачи С1 из ЕГЭ 2011 года.

Существуют тригонометрические уравнения, в которых нужно производить отбор корней при выписке ответа. Это связано с некоторыми ограничениями, например: знаменатель дроби не равен нулю, выражение под корнем четной степени неотрицательно, выражение под знаком логарифма положительно и т.д.

Такие уравнения считаются уравнениями повышенной сложности и в варианте ЕГЭ находятся во второй части, а именно С1.

Дробь равна нулю, если тогда с помощью единичной окружности произведем отбор корней (см. рисунок 1)

получим x = π + 2πn, n Z

Ответ: π + 2πn, n Z

На экране отбор корней показывается на окружности в цветном изображении.

Произведение равно нулю когда хотя бы один из множителей равен нулю, а дугой, при этом, не теряет смысла. Тогда

С помощью единичной окружности отберем корни (см. рисунок 2)

тогда ,

Ответ: .

3) (2cos 2 x + 5cosx + 2) log₅(tgx) = 0

Вспоминаем когда произведение равно нулю и переходим к системе:

отметим на единичной окружности корни уравнений и выберем из них те, которые удовлетворяют неравенствам (см. рисунок 3),

получим

Ответ:

Вспоминаем когда дробь равна нулю и переходим к системе:

решив первое уравнение, получаем

с помощью единичной окружности выбираем корни (см. рисунок 4),

получаем x = π/6 + 2πn, n Z

Ответ: π/6 + 2πn, n Z.

Переходим к системе:

В первом уравнении системы сделаем замену log₂(sinx) = y, получим уравнение тогда , вернемся к системе

с помощью единичной окружности отберем корни (см. рисунок 5),

6. Самостоятельная работа (15 мин.)

Цель – закрепить и проверить усвоение материала, выявить ошибки, наметить пути их исправления.

Работа предлагается в трех вариантах, заготовленных заранее на печатной основе, на выбор учащихся.

Решать уравнения можно любым способом.

2) (2sinx + √3)log₈(cosx) = 0

7. Итог урока, домашнее задание (5 мин.)

Учитель подводит итог урока, еще раз обращается внимание на то, что тригонометрическое уравнение можно решить несколькими способами. Самый лучший способ для достижения быстрого результата это тот, который лучше всего усвоен конкретным учеником.

При подготовке к экзамену нужно систематически повторять формулы и методы решения уравнений.

Домашнее задание (приготовлено заранее на печатной основе) раздается и комментируются способы решений некоторых уравнений.

1) cosx + cos5x = cos3x + cos7x

3) 4sin 2 x + sin2x = 3

5) cos3x cos6x = cos4x cos7x

7) 3sin2x + 4 cos2x = 5

8)cosx cos2x cos4x cos8x = (1/8)cos15x

11)

Источник