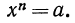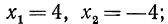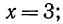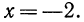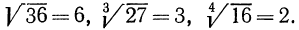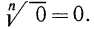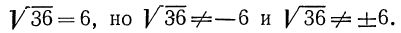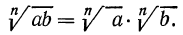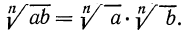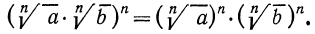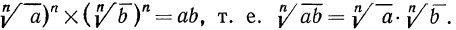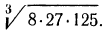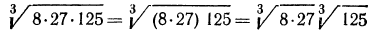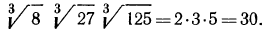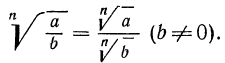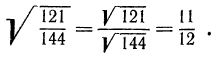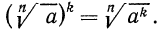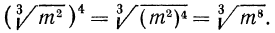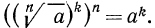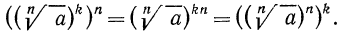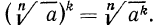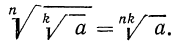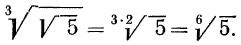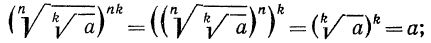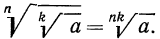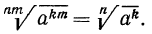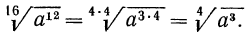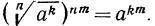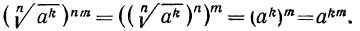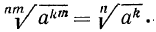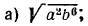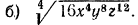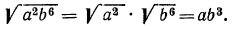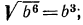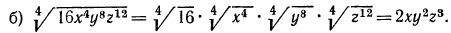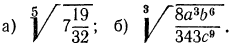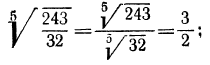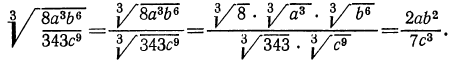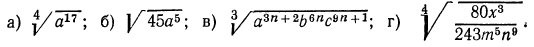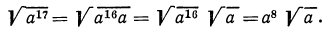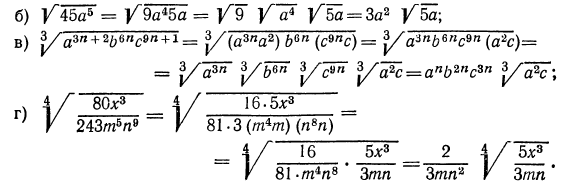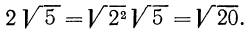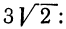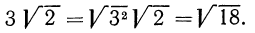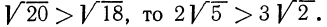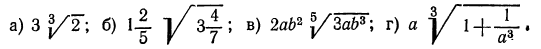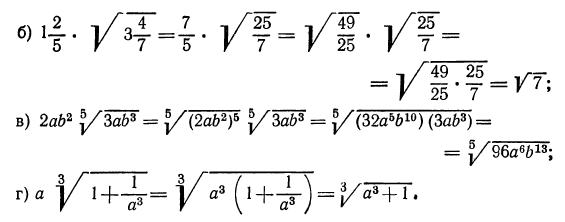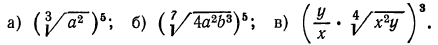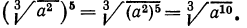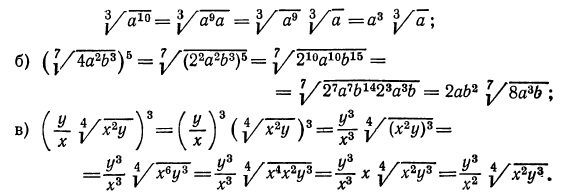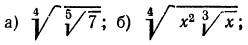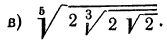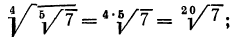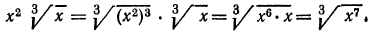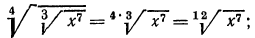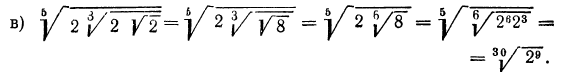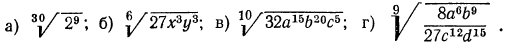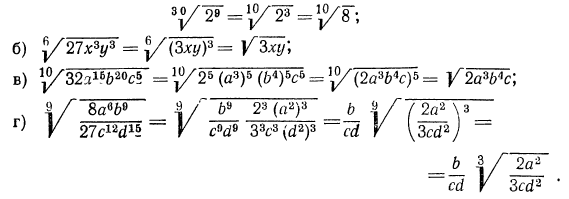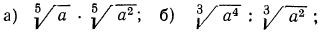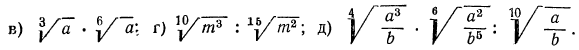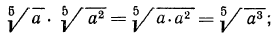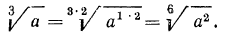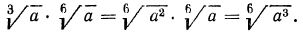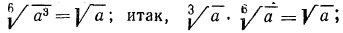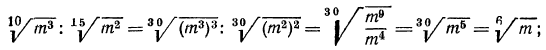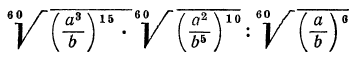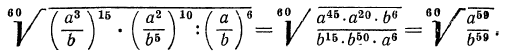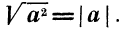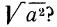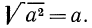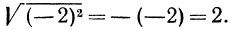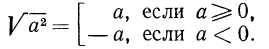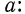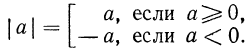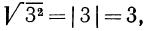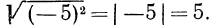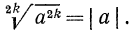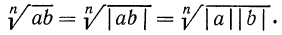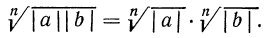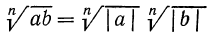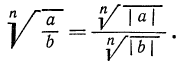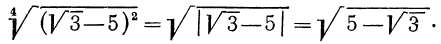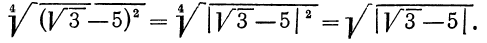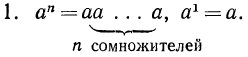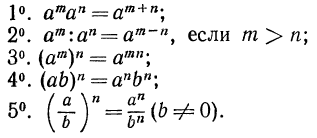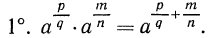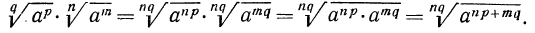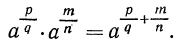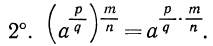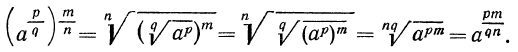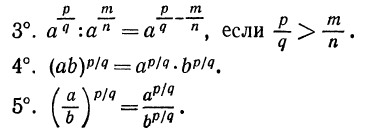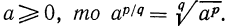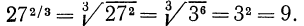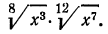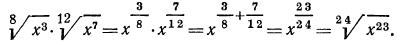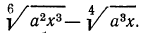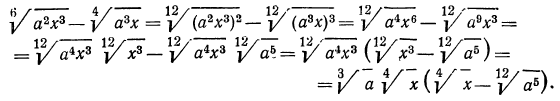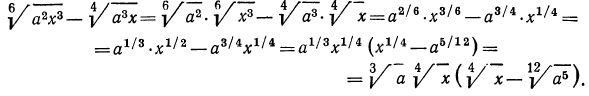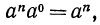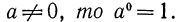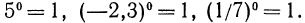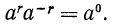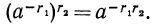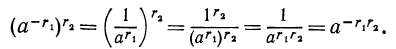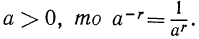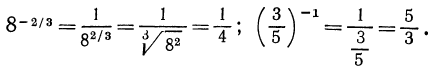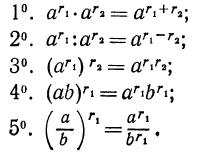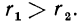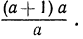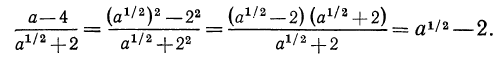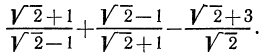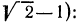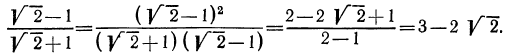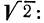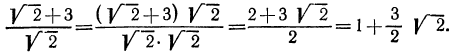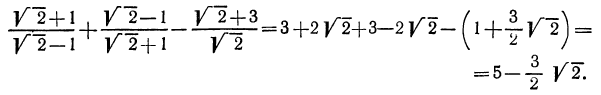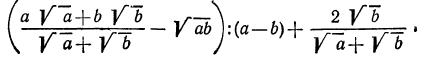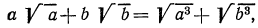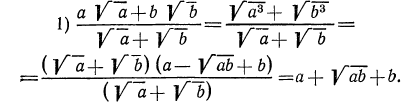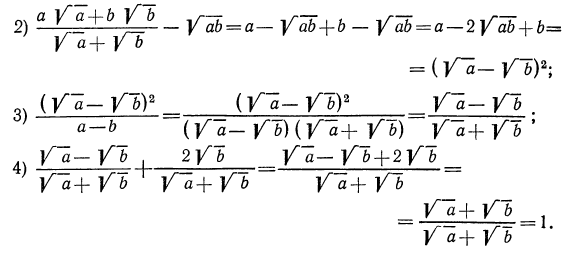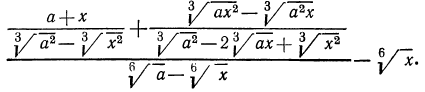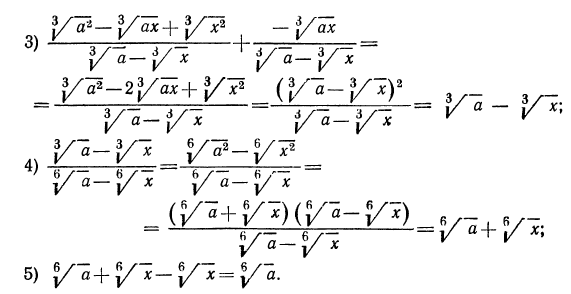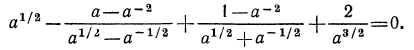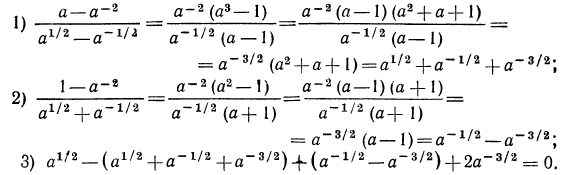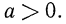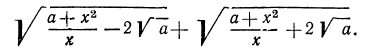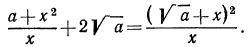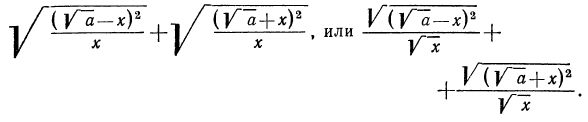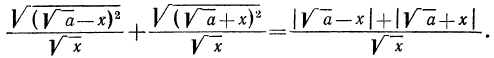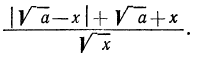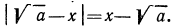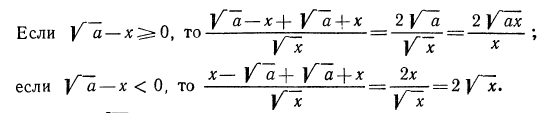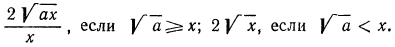Как упрощать выражения с корнями

Корень и его свойства

Тема в математике «Корень и его свойства» нередко вызывает затруднения у школьников, особенно при решении примеров. В данной статье описаны основные свойства корней, а также правила сложения, вычитания, умножения и деления. Наглядные примеры помогаю понять, как решать задания с корнями.

Определение «Корень»

Корень второй степени (квадратный корень) из числа a — это число, которое становится равным a, если число a возвести во вторую степень (в квадрат).
Например, √ 64 = 8 (√ 64 равно числу 8).

Формула: √ a 2 = a

Число, стоящее под знаком корня, называется подкоренным числом. Если под знаком корня стоит целое выражение, то его называют подкоренным выражением.
Свойство квадратного корня: для действительных чисел не существует квадратный корень из отрицательного числа, так как возведение числа в квадрат будет всегда неотрицательным числом.

Извлечение корней: примеры

Найти корень из числа можно одним из следующих способов:

Приведение корней с разными показателями

Для того, чтобы упростить выражение с корнями, которое содержит корни разных степеней, необходимо привести все корни к одной степени.

Например, есть квадратный корень (второй степени √ 2 ) и кубический корень (третьей степени 3 √ 3 ).
Во-первых, необходимо найти наименьшее общее кратное (НОК) для степеней. В нашем примере НОК=6 (2х3).
Во-вторых, применим свойство a = n √ a n : √ 2 = 2 √ 2 = 6 √ 2 3 = 6 √ 8 ; 3 √ 3 = 6 √ 3 2 = 6 √ 9
Получилось два корня одинаковой степени, с которыми можно совершать различные математические действия.

Корень: сложение и вычитание корней

Основное правила сложения и вычитания квадратных корней: сложение и вычитание квадратного корня возможны только при условии одинакового подкоренного выражения.

Примеры:
2√ 3 + 3√ 3 = 5√ 3
2√ 3 + 2√ 4 – не выполняется.

Алгоритм действия:
1. Упростить подкоренное выражение путем разложения на простые множители.
2. Затем нужно извлечь корень из квадратного числа и записать полученное значение перед знаком корня.
3. После процесса упрощения необходимо подчеркнуть корни с одинаковыми подкоренными выражениями — только их можно складывать и вычитать.
4. У корней с одинаковыми подкоренными выражениями необходимо сложить или вычесть множители, которые стоят перед знаком корня. Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!

Корень: умножение

Умножение корней без множителей

Произведение корней из чисел равно корню из произведения этих чисел.
√ a*b =√ a *√ b
Важно: между собой можно умножать только одинаковые степени корней, то есть можно умножить один квадратный корень на другой, но нельзя умножить квадратный корень на корень кубической степени.
Примеры:
√ 2 х √ 3 = √ 6
√ 6 х √ 3 = √ 18 = √ 3х3х2 = 3√ 2

Умножение корней с множителями

При умножении корней с множителями нужно отдельно перемножить множители и подкорневые выражения (числа). Подкорневые числа можно перемножать между собой только в том случае, если они имеют одинаковые степени (см. умножение корней без множителей). В случае отсутствия множителя, он равен единице.
Примеры:
3√ 2 х √ 5 = (3х1) √ (2*5) = 3√ 10
4√ 2 х 3√ 3 = (3х4) √ (2х3) = 12√ 6

Корень: деление

Основной правило деления — подкоренные выражения делятся на подкоренные выражения, а множители на множители.
√ a:b =√ a :√ b
В процессе деления квадратных корней дроби упрощаются.

Деление корней без множителей

Частное корней из чисел равно корню из частного этих чисел.
Важно: между собой можно делить только одинаковые степени корней, то есть можно делить один квадратный корень на другой, но нельзя делить квадратный корень на корень кубической степени.
Пример. √ 21 :√ 3 =√ 21:3 =√ 7

Деление квадратных корней с множителями

Примеры для практики

Чтобы попрактиковаться решать примеры на вычисление квадратный корней, можно скачать программу «Корни квадратные«

Источник

Иррациональные выражения (выражения с корнями) и их преобразование

Статья раскрывает смысл иррациональных выражений и преобразования с ними. Рассмотрим само понятие иррациональных выражений, преобразование и характерные выражения.

Что такое иррациональные выражения?

При знакомстве с корнем в школе мы изучаем понятие иррациональных выражений. Такие выражения тесно связаны с корнями.

Иррациональные выражения – это выражения, которые имеют корень. То есть это выражения, имеющие радикалы.

Основные виды преобразований иррациональных выражений

При вычислении таких выражений необходимо обратить внимание на ОДЗ. Часто они требуют дополнительных преобразований в виде раскрытия скобок, приведения подобных членов, группировок и так далее. Основа таких преобразований – действия с числами. Преобразования иррациональных выражений придерживаются строгого порядка.

Необходимо выполнить замену числа 9 на выражение, содержащее корень. Тогда получаем, что

Полученное выражение имеет подобные слагаемые, поэтому выполним приведение и группировку. Получим

Результат тождественных преобразований привел к произведению двух рациональных выражений, которые необходимо было найти.

Можно выполнять ряд других преобразований, которые относятся к иррациональным выражениям.

Преобразование подкоренного выражения

Использование свойств корней

Для правильного преобразования используют преобразования иррациональных выражений с использованием свойств корней.

Внесение множителя под знак корня

Вынесение множителя из-под знака корня

Вынесение множителя из-под корня необходимо для упрощения выражения и его быстрого преобразования.

Преобразование дробей, содержащих корни

Необходимо обратить внимание на то, что необходимо изменять знак только числителя или только знаменателя. Получим, что

Сокращение дроби чаще всего используется при упрощении. Получаем, что

Перед сокращением необходимо выполнять преобразования, которые упрощают выражение и дают возможность разложить на множители сложное выражение. Чаще всего применяют формулы сокращенного умножения.

Сокращение дробей или приведение подобных необходимо только на ОДЗ указанной дроби. При умножении числителя и знаменателя на иррациональное выражение получаем, что мы избавляемся от иррациональности в знаменателе.

Избавление от иррациональности в знаменателе

Переход от корней к степеням

Источник

Преобразование иррациональных выражений в математике с примерами решения и образцами выполнения

Иррациональными выражениями называют выражения, содержащие операцию извлечения корня. Другими словами, иррациональные выражения – это выражения с радикалами (выражения, содержащие в своей записи знаки корня).

Арифметический корень и его свойства

Определение арифметического корня: Пусть а—действительное число, a n — натуральное число, большее единицы. Поставим перед собой задачу: найти число х, такое, чтобы выполнялось равенство

Сначала рассмотрим конкретные примеры.

тогда равенство (1) принимает вид: откуда

тогда равенство (1) принимает вид: откуда

тогда равенство (1) принимает вид: что не выполняется ни при каком действительном значении х;

тогда равенство (1) принимает вид: откуда

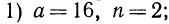
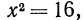
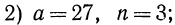
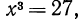
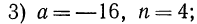
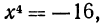
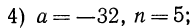
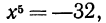
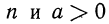
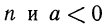
Эти примеры показывают, что поставленная задача при четном имеет два решения, при нечетном n —одно решение, при четном ни одного решения.

Если задача имеет решение, т. е. равенство 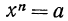выполняется при некоторых значениях х, то эти значения x называются корнями n-й степени из числа а итак корень n-й степени из числа а—это такое число, n-я степень которого равна а.

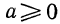
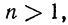
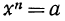
Рассмотрим случай отыскания корня n-й степени из неотрицательного числа. Можно доказать, что если и то существует и только одно неотрицательное число х, такое, что (доказательство проводится в курсе высшей математики; представление об этом доказательстве будет дано в следующей главе).

Арифметическим корнем n-й степени из положительного числа а называется такое положительное число, n-я степень которого равна а.

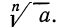
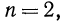
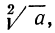
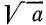
Для арифметического корня n-й степени из числа а принято обозначение Число а называется подкоренным числом или подкоренным выражением, n- показатель корня. Если то обычно не пишут а пишут просто и называют это выражение квадратным корнем. Часто вместо термина «корень» используется термин «радикал».

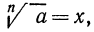
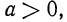
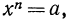
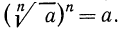
Согласно определению запись где означает, во-первых, что и, во-вторых, что т. е. Например,

Полагают также

Обратим внимание читателя на то, что, например,

Свойства арифметических корней

Условимся прежде всего о следующем: все переменные, которые встречаются в формулировках свойств и в примерах, рассматриваемых в настоящем и следующем пунктах, будем считать принимающими только неотрицательные значения. Кроме того, мы рассматриваем только арифметические корни, а потому каждый раз специально подчеркивать это не будем. Значит, мы будем писать: «корень n-й степени из неотрицательного числа», а читатель должен понимать, что речь идет об арифметическом корне.

1°. Корень n-й степени из произведения двух неотрицательных чисел равен произведению корней из этих чисел, т. е.

Доказательство:

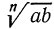
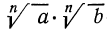
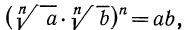
Мы знаем, что это такое неотрицательное число, которое, будучи возведено в степень n, дает подкоренное выражение ab. Ясно, что — неотрицательное число. Значит, если мы покажем, что то это и будет обозначать, что

Итак, рассмотрим выражение 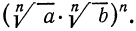По свойству 1° степени с натуральным показателем (стр. 45) имеем

Так как 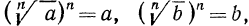то получаем

Пример. Вычислить

Решение. По свойству 1° имеем

2°. Корень n-й степени из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, деленному на корень из знаменателя, т. е.

Пример:

Доказательство этого свойства аналогично доказательству свойства 1°.

3°. Чтобы возвести корень n-й степени в натуральную степень k, достаточно возвести в эту степень подкоренное выражение и из полученного результата извлечь корень n-й степени, т. е.

Пример:

Доказательство:

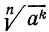
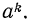
По определению корня это такое неотрицательное число, которое, будучи возведено в n-ю степень, дает Поэтому нам достаточно показать, что

По свойству 3° степени с натуральным показателем (стр. 45) имеем

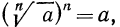
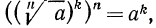
Так как то получаем т. е.

4°. Чтобы извлечь корень из корня, нужно перемножить показатели корней, а подкоренное выражение оставить без изменения, т. е.

Пример:

Доказательство:

значит,

5°. Если показатель корня и показатель степени подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится, т. е.

Пример:

Доказательство:

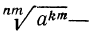
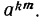
По определению корня это такое неотрицательное число, которое, будучи возведено в степень mn дает Значит, достаточно показать, что

По свойству 3° степени с натуральным показателем имеем

Значит,

Примеры:

Извлечь корень из произведения:

Решение:

а) Применив свойство 1° арифметических корней, получим:

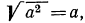
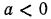
Напомним, что мы в начале рассматриваемого пункта условились считать все переменные принимающими только неотрицательные значения. Не будь этого соглашения, мы не имели бы права писать так как при это неверно; то же относится и к равенству

2. Извлечь корень из дроби

Решение:

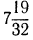
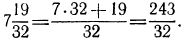
а) Обратим смешанное число в неправильную дробь: свойству 2° получаем

б) воспользовавшись свойствами 2° и 1°, получим

3.Вынести множитель из-под знака корня:

Решение:

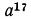
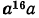
а) Представим подкоренное выражение в виде и применим к полученному произведению свойство 1° арифметических дробей:

Такое преобразование называется вынесением множителя из-под знака корня. Цель преобразования —упрощение подкоренного выражения;

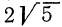
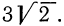
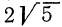
В некоторых случаях оказывается полезным преобразование, в определенном смысле обратное только что рассмотренному, а именно: внесение множителя под знак корня. Пусть, например, нужно выяснить, какое из чисел больше: или Рассмотрим число Внесем множитель 2 под знак корня —это достигается с помощью следующего преобразования:

Сделаем аналогичное преобразование числа

Так как

4.Ввести множитель под знак корня:

Решение:

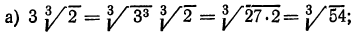
В рассмотренных примерах мы пользовались только определением корня и свойствами 1° и 2°. Рассмотрим теперь примеры использования свойств 3° и 4°.

Решение:

а) По свойству 3° имеем

Обычно стараются подкоренное выражение упростить, для чего выносят множители за знак корня. Имеем:

6.Выполнить действия:

Решение:

а) По свойству 4° арифметических корней имеем

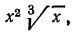
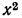
б) преобразуем выражение внеся множитель под знак корня:

Далее имеем

Рассмотрим, наконец, примеры, в которых используется свойство 5°.

Решение:

а) По свойству 5° мы имеем право показатель корня и показатель степени подкоренного выражения разделить на одно и то же натуральное число. Если в рассматриваемом примере разделить указанные показатели на 3, то получим

8.Упростить выражения:

Решение:

а) Из свойства 1° получаем, что для перемножения корней одной и той же степени достаточно перемножить подкоренные выражения, из полученного результата извлечь корень той же степени; значит,

в) выше мы видели, как перемножить корни одной и той же степени. В данном же примере требуется перемножить корни с различными показателями. Значит, прежде всего мы должны привести радикалы к одному показателю. Согласно свойству 5°, можно показатель корня и показатель степени подкоренного выражения умножить на одно и то же натуральное число; поэтому

А теперь разделим в полученном результате показатели корня и подкоренного выражения на 3:

г) приведем радикалы к одному показателю. Для этого, очевидно, нужно найти наименьшее общее кратное чисел 10 и 15; 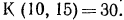Значит, нам нужно показатели корня и степени подкоренного выражения для первого из перемножаемых радикалов умножить на 3, а для второго—на 2; получим

д) НОК чисел 4, 6, 10 равно 60, поэтому приведем все радикалы к показателю 60:

Тождество

Ответим на такой вопрос: если переменная а принимает как неотрицательные, так и отрицательные значения, то чему равен

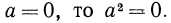
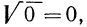
Если Но значит можно считать, что при справедливо равенство

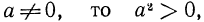
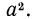
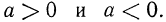
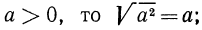
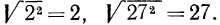
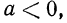
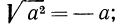
Если и речь, следовательно, идет об арифметическом корне второй степени из положительного числа Здесь могут представиться два случая: Если например, Если же то например,

Итак, можно записать, что

Но точно так же определяется модуль действительного числа

Таким образом, 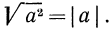Например,

Вообще, если n — четное число, т.е. 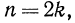то

Так, если в рассмотренных примерах 1, а) и б) снять требование неотрицательности значений переменных, то решение примера выглядело бы следующим образом:

Дополнительные замечания о свойствах радикалов

Рассмотренные пять свойств арифметических корней, т. е. пять свойств радикалов безоговорочно верны для неотрицательных подкоренных выражений. Но при решении примеров на действия с радикалами нужно иметь в виду возможность отрицательных значений переменных, содержащихся под знаками радикалов.

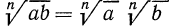
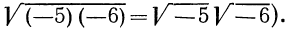
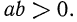
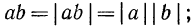
Пусть а и b — отрицательные числа, а n — четное число. В этом случае написать нельзя, так как 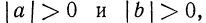правая часть такого «равенства» не имеет смысла (например, нельзя написать Здесь можно рассуждать так: а и b—отрицательные числа, следовательно, Но тогда значит,

Так как то, применив свойство 1° арифметических корней, получим

Итак, если n —четное число, а числа а и b имеют одинаковые знаки, то

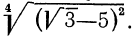
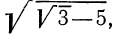
Очень внимательно следует относиться к свойству 5°. Пусть, например, нужно упростить выражение Если разделить показатели корня и подкоренного выражения на 2, то придем к выражению не имеющему смысла, так как под корнем четной степени содержится отрицательное число. Верное равенство в данном случае выглядит так:

В самом деле, 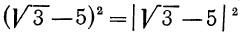и, следовательно,

Обобщение понятия о показателе степени

Постановка задачи: Напомним определение степени с натуральным показателем и ее свойства.

Определение

Основные свойства степени

В последующих пунктах речь пойдет об определениях степени с любым рациональным показателем.

Сначала мы определим степень с положительным дробным показателем, далее степень с нулевым показателем и затем степень с отрицательным рациональным показателем. Ясно, что ни на один из этих случаев не переносится данное выше определение, например 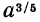нельзя определить как произведение числа а самого на себя 3/5 раза. Поэтому каждый раз придется вводить новое определение. При выборе нового определения мы будем руководствоваться требованием, чтобы на новый случай степени распространялись свойства, аналогичные свойствам 1°—5°, перечисленным выше.

Степень с положительным дробным показателем

Пусть Надо определить так, чтобы выполнялось, например, равенство т. е. чтобы при возведении степени в степень показатели перемножались. Но это равенство возможно лишь в случае, когда Возникает вполне естественная мысль: определить Но будет ли такое определение удачным, т. е. будут ли при таком определении выполняться свойства, аналогичные свойствам 1°—5°? Проверим это.

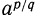
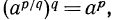
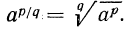
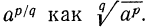
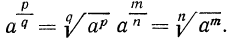
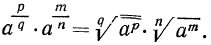
Доказательство. Согласно предложенному определению степени с положительным дробным показателем имеем: Значит, Воспользовавшись свойствами радикалов, приведем радикалы к одному показателю и выполним умножение:

Далее имеем 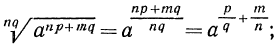значит,

Доказательство:

Воспользуемся свойствами возведения радикала в степень и извлечения корня из корня:

Аналогично можно показать, что будут выполняться свойства:

Итак, при предложенном определении степени с положительным дробным показателем основные свойства степени выполнены. Значит, определение удачно и его можно принять.

Определение:

Если

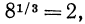
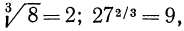
Например, так как так как

На практике при выполнении действий над радикалами довольно часто переходят к дробным показателям.

Примеры:

Выполнить умножение:

Решение:

2.Разложить на множители

Решение:

Степень с нулевым показателем

При выборе определения мы также будем руководствоваться требованием, чтобы на случай степени с нулевым показателем распространялись свойства 1°—5° степени с натуральным показателем (впрочем, теперь мы уже вправе говорить о распространении свойств степени с положительным рациональным показателем). В частности, при умножении степеней с одинаковым основанием показатели должны складываться, т. е. должно выполняться равенство

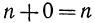
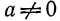
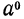
так как (n—натуральное число). Это равенство при возможно лишь в случае, когда Поэтому возникает мысль определить как 1. Нетрудно проверить, что при таком определении выполняются свойства, аналогичные свойствам 1° — 5° степени с натуральным показателем, значит, определение можно принять.

Определение:

Если

Например,

Степень с отрицательным рациональным показателем

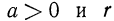
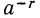
Пусть положительное рациональное число. Надо определить так, чтобы, например, выполнялось равенство

Покажем, например, что

Остальные свойства проверяются аналогично.

Определение:

Если

Например,

Замечание:

Если r—целое число, то полагают а 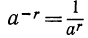и в случае, когда а Степень с любым рациональным показателем

Мы определили понятие степени с любым рациональным показателем. Эта степень обладает следующими свойствами (мы полагаем а > 0, b > 0, 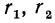— произвольные рациональные числа):

Заметим, что после введения нулевого и отрицательного показателей мы имеем право в свойстве 2° не делать оговорки, что

Тождественные преобразования иррациональных выражении

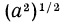
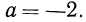
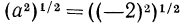
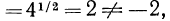
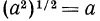
Тождественно равные выражения на данном множестве: По определению (стр. 47) тождественно равными выражениями называются такие, у которых все соответственные значения равны. Согласно этому определению выражения и а не являются тождественно равными. Действительно, пусть тогда т. е. равенство не является тождеством.

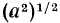
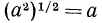
Однако на множестве всех неотрицательных чисел все соответственные значения выражений и а равны и равенство называют тождеством на этом множестве.

Определение:

Два выражения называются тождественно равными на данном множестве, если на этом множестве они имеют смысл и все их соответственные значения равны.

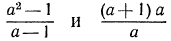
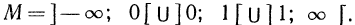
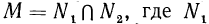
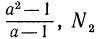
Например, выражения тождественно равны на множестве Легко видеть, что где TV, — множество, на котором определено выражение множество, на котором определено выражение

Тождественные преобразования иррациональных выражений

Выражение с переменными называется иррациональным, если оно содержит извлечение корня из переменной или возведение переменной в дробную степень.

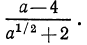
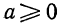
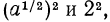
Тождественные преобразования иррациональных выражений выполняются, как правило, на множестве неотрицательных чисел. Это вытекает из введенных ранее определений. Например, сократим дробь При выражение а — 4 можно представить в виде разности квадратов выражений а затем сократить дробь:

Проделанное нами тождественное преобразование выполнено на множестве неотрицательных чисел, т. е. при В дальнейшем мы будем это подразумевать и специально не оговаривать.

Примеры:

Решение:

Здесь целесообразно применить прием избавления от иррациональности в знаменателе. Для этого умножим числитель и знаменатель первой дроби на 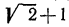(это выражение называется сопряженным для

Аналогично поступим со второй дробью (теперь выражением, сопряженным для знаменателя, является

Для того чтобы избавиться от иррациональности в знаменателе третьей дроби, умножим числитель и знаменатель этой дроби на

Таким образом, имеем

Решение:

Прежде всего подумаем, нельзя ли сократить первую дробь. Выражение, стоящее в числителе, можно преобразовать так:

Таким образом, последовательное сокращение дробей при тождественных преобразованиях иррациональных выражений обеспечивает достаточную простоту решения. Проиллюстрируем эту мысль еще на одном примере.

Решение:

Попытка привести дроби, стоящие в числителе, к общему знаменателю без предварительных сокращений этих дробей приведет решение к неоправданному усложнению. Поэтому в первую очередь надо сократить эти дроби, а затем произвести указанные действия:

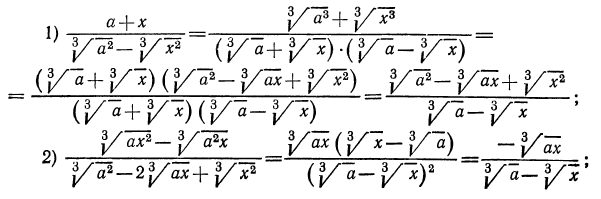
Идея сокращения дробей лежит и в основе тождественных преобразований выражений, содержащих степени с рациональными показателями.

Решение:

Подчеркнем, что проделанные нами в примере 4 тождественные преобразования выполнены на множестве положительных чисел, т. е. при

Иногда множество, на котором выполняются преобразования, имеет более сложную природу. Поясним это на следующем примере.

Решение:

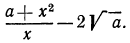
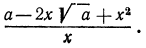
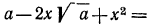
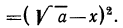
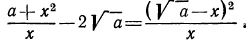
Рассмотрим выражение Оно преобразуется к виду Замечаем, что Итак, Аналогично

После этих наблюдений мы можем заданное выражение переписать в виде

Выше мы отмечали, что 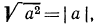поэтому

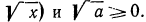
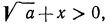
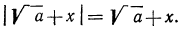
По смыслу примера имеем (заданное выражение содержит Значит, а потому Таким образом, мы приходим к выражению

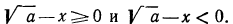
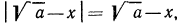
Теперь нужно рассмотреть два случая: В первом случае а во втором

Ответ:

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник