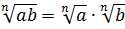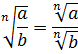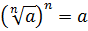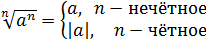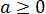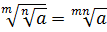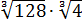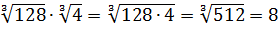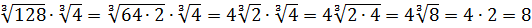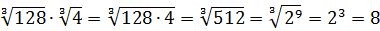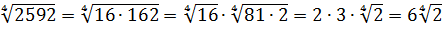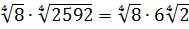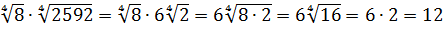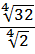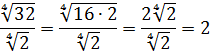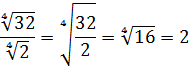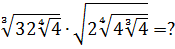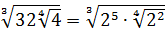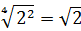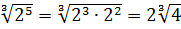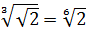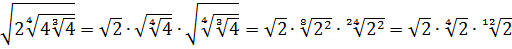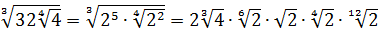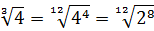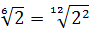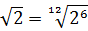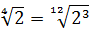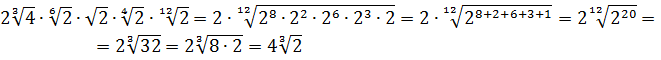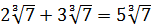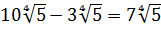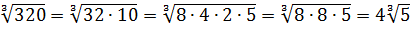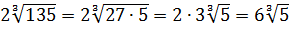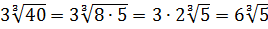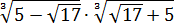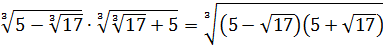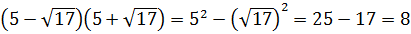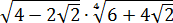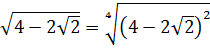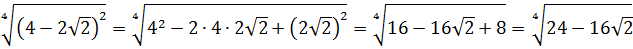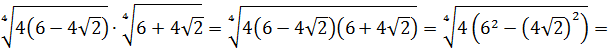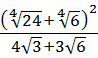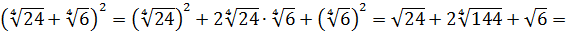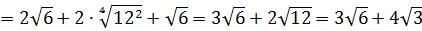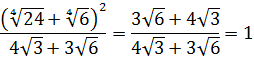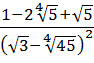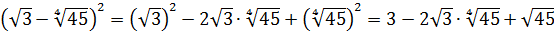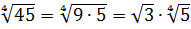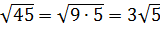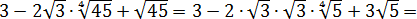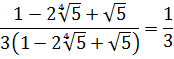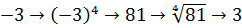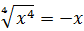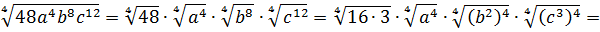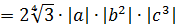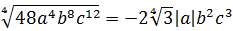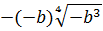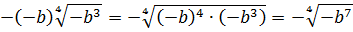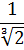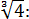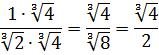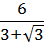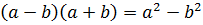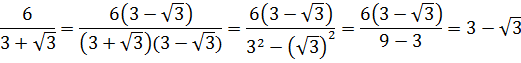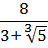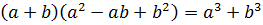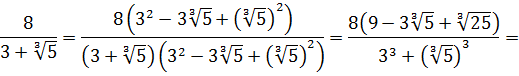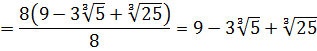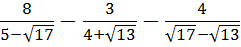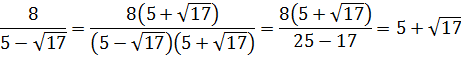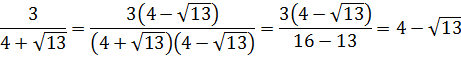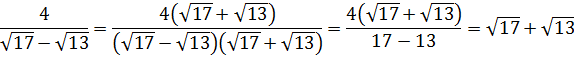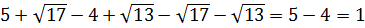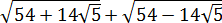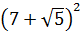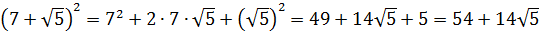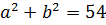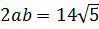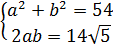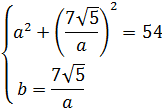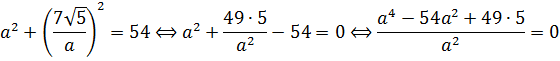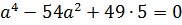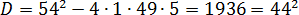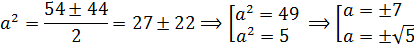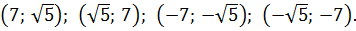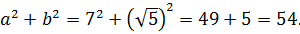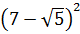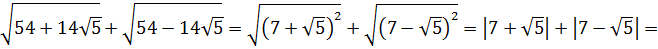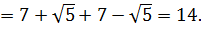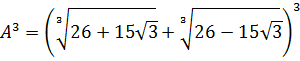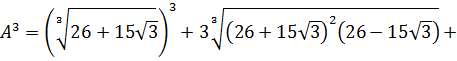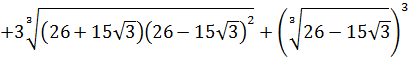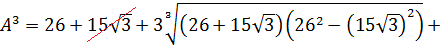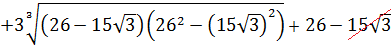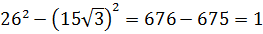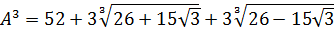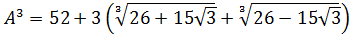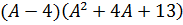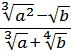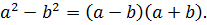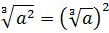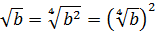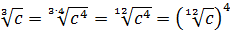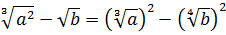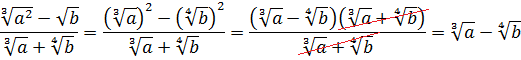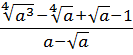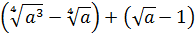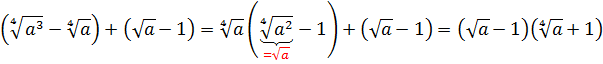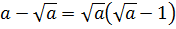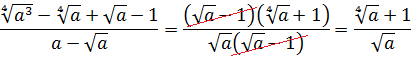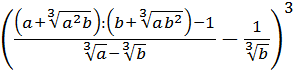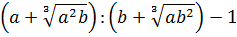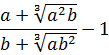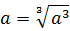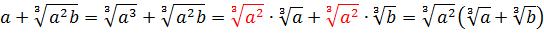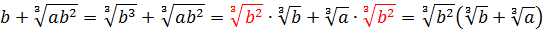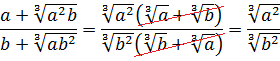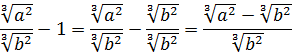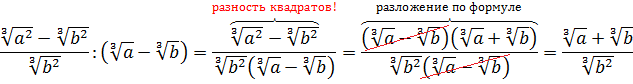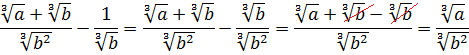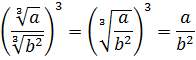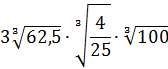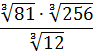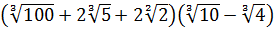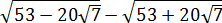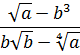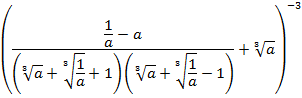Как упрощать квадратные выражения
Упрощения алгебраических выражений
Что значит упростить алгебраическое выражение
Алгебраическое выражение — одна или несколько алгебраических величин (чисел и переменных), которые объединены с помощью знаков арифметических действий в виде сложения, вычитания, умножения, деления, извлечения корня, возведения в степень (при целых значениях показателей корня и степени), знаков последовательности, определяющих порядок применения данных операций (скобки разного вида).
Обязательным условием для алгебраического выражения является конечное число величин, которые его составляют. Данный принцип пригодиться математикам для решения задач в средних классах школы.
Упростить выражение — это значит уменьшить число арифметических действий, необходимых для вычисления значения данного выражения с учетом определенных значений переменных.
Правила упрощения алгебраических выражений
Существуют основные методы в алгебре для того, чтобы упростить алгебраическое выражение:
В процессе приведения выражения в более простую форму следует использовать полезные советы:
Приведение подобных
Приведение подобных слагаемых в теории заключается в сложении их коэффициентов и приписывании буквенной части.
Подобными являются слагаемые (одночлены), которые обладают буквенной частью.
В выражении 2ab+3ab+b одночлены 2ab и 3ab являются подобными слагаемыми.
Привести подобные — значит, выполнить сложение нескольких подобных слагаемых для получения в результате одного слагаемого.
К примеру, приведем слагаемые:
Заметим, что числа в таких слагаемых умножают на буквы. Данные числа носят названия коэффициентов.
Рассмотрим выражение с квадратной степенью:
Здесь число 3 является коэффициентом.
Разложение на множители
Разложить выражение на множители можно, если вынести общий множитель за скобки, применить формулы сокращенного умножения и другие.
a b 2 + a 2 c = a b 2 + a c
В распространенных случаях разложение на множители следует за приведением подобных при упрощении выражений. В итоге получаются произведения. Чтобы это понять, отдельно нужно упомянуть правила действия с дробями, а именно, при сокращении дроби числитель и знаменатель требуется записать, как произведения.
Сокращение дроби
В процессе сокращения дроби допустимо выполнять умножение или деление числителя и знаменателя дроби на одинаковое число, отличное от нуля, в результате чего величина дроби остается прежней.
Объяснение алгоритм действий при сокращении дробей:
a a + b a 2 = a a + b a · a = a + b a
Важно заметить, что сокращению подлежат исключительно множители.
Озвученное правило является следствием ключевого свойства дроби. Оно состоит в допустимости умножения или деления числителя и знаменателя дроби на одно и то же число, которое не равно нулю. В результате значение дроби останется без изменений.
Существует простой способ, руководствуясь которым можно определить, разложено ли выражение на множители. Арифметическое действие, выполняемое в последнюю очередь при вычислении значения выражения, считается «главным».
Данное правило состоит в том, что, когда при подстановке каких-либо чисел на замену буквам и вычислении значения выражения последнее действие представляет собой умножение, можно заключить, что перед нами произведение, то есть выражение разложено на множители. В том случае, когда на последнем шаге в процессе расчетов выполняется сложение или вычитание, разложение выражения на множители не выполнено, то есть сокращение не допускается.
Сложение и вычитание дробей
При сложении и вычитании обыкновенных дробей требуется найти общий знаменатель, умножить каждую из дробей на недостающий множитель и сложить или вычесть числители:
a b + c d = a · d + c · b b · d ;
Разберем правило на конкретных примерах. Вычислим:
Заметим, что знаменатели являются взаимно простыми, то есть не имеют общих множителей. Таким образом, наименьший общий множитель данных чисел соответствует их произведению. В результате:
В данном случае общим множителем является число 24. Выполним преобразования и упростим выражение:
В данном примере следует смешанные дроби записать в виде неправильных. Далее можно упростить выражение по стандартному алгоритму:
Разберем самостоятельный случай, когда знаменатели не содержат буквы. При этом алгоритм действий такой же, как и при действиях с обыкновенными дробями:
Здесь общий множитель равен 12. Тогда:
a 2 b · 3 4 + a · 2 6 = 3 a 2 b + 2 a 12
Далее можно привести подобные в числители, и разложить на множители при их наличии:
a 2 b 4 + a 6 = 3 a 2 b + 2 a 12 = a 3 a b + 2 12
Когда знаменатели содержат буквы, схема действий существенно не меняется:
Рассмотрим пример, когда требуется упростить выражение:
Разложим знаменатели на множители:
a b 2 = a · b · b a 2 b = a · a · b
Вычислим единые множители:
a b 2 = a ¯ · b ¯ ¯ · b a 2 b = a ¯ · a · b ¯ ¯
Затем можно записать общие множители и выполнить умножение:
a ¯ · b ¯ ¯ · a · b = a 2 b 2
1 a b 2 · a + 1 a 2 b · b = a + b a 2 b 2
Умножение и деление дробей
Умножение и деление дробей выполняют таким образом:
a b · c d = a · c b · d ;
a b : c d = a · d b · c
Арифметические действия выполняют в следующем порядке:
Важно заметить, что при наличии скобок, операции, которые в них заключены, необходимо выполнить в первую очередь. Далее можно приступать к раскрытию скобок. Когда имеется несколько скобок с арифметическими действиями, которые нужно умножить или разделить, в начале проводят вычисления в каждой из скобок, а затем умножение или деление полученных результатов. При наличии внутренних скобок, заключенных в скобки, действия в них выполняют в первую очередь.
Используя правило умножения и деления дробей, получим:
Во многих примерах имеются не только цифры, но и буквы. В этом случае выполняются алгебраические действия, в том числе, приведение подобных, сложение, сокращение дробей и другие операции. Отличия можно заметить при разложении многочленов на множители. Для этого следует пользоваться формулами сокращенного умножения или вынесением единого множителя за скобки.
Ключевой задачей при работе с такими выражениями является запись выражений в виде произведения или частного.
Попробуем упростить выражение:
Так как имеются скобки, следует начать преобразования именно с них. Упростим разность дробей, которая в них записана, чтобы получить вместо нее произведение или частное. Приведем дроби к единому знаменателю и определим сумму:
Заметим, что дальнейшие преобразования не приведут к упрощению данного выражения. Причина этого заключается в том, что каждый из множителей является элементарным. В результате:
Пояснения на примерах
Требуется упростить выражения:
Приведем подобные и упростим выражения:
Заметим, что ab и 2ba являются подобными по той причине, что:
В результате можно сделать вывод, что данные слагаемые обладают одинаковой буквенной частью.
Требуется упростить выражения:
Путем разложения на множители упростим данные выражения:
a b 2 + a 2 c = a b 2 + a c
72 30 = 2 · 2 · 2 · 3 · 3 2 · 3 · 5 = 2 · 2 · 2 · 3 · 3 2 · 3 · 5 = 2 · 2 · 3 5 = 12 5
a a + b a 2 = a a + b a · a = a + b a
В первую очередь выполним разложение на множители:
Дано выражение, которое требуется упростить:
В данном случае требуется разложить знаменатели на множители. Первый знаменатель записан так, что можно вынести за скобки х. Второй знаменатель содержит разность квадратов. Выполним преобразования:
Рассмотрим выражение на наличие общих множителей:
Заметим, что при переносе слагаемых, заключенных в скобках, изменился знак перед дробью. Приведем выражения к единому знаменателю:
Воспользуемся формулой сокращенного умножения, а именно, разностью кубов:
Заметим, что в знаменателе дроби расположено выражение, которое называют неполным квадратом суммы:
x 2 + 2 x + 4 = x 2 + 2 · x + 2 2
Второе по счету слагаемое в неполном квадрате суммы является произведением первого и последнего. Неполный квадрат суммы представляет собой множитель, который входит в состав разложения разности кубов:
Требуется упростить выражения:
Дано выражение, которое требуется упростить:
При наличии в знаменателях одного и того же множителя, возведенного в разные степени, то в общем знаменателе данный множитель будет обладать самой большой из имеющихся степеней. Применительно к этой задаче, общий знаменатель будет состоять из следующих выражений:
a во второй степени;
x в третьей степени;
b в третьей степени;
y в четвертой степени.
В результате получим:
Нужно упростить выражение:
Исключить ошибки можно, если расписать заранее порядок операций. В первую очередь целесообразно суммировать дроби, расположенные в скобках. В результате будет получена только одна дробь. Далее можно приступить к делению дробей. Полученный итог следует прибавить к последней дроби.
Выглядит этот алгоритм таким образом:
Корень и его свойства
Определение «Корень»
Корень второй степени (квадратный корень) из числа a — это число, которое становится равным a, если число a возвести во вторую степень (в квадрат).
Например, √ 64 = 8 (√ 64 равно числу 8).
Формула: √ a 2 = a
Число, стоящее под знаком корня, называется подкоренным числом. Если под знаком корня стоит целое выражение, то его называют подкоренным выражением.
Свойство квадратного корня: для действительных чисел не существует квадратный корень из отрицательного числа, так как возведение числа в квадрат будет всегда неотрицательным числом.
Извлечение корней: примеры
Найти корень из числа можно одним из следующих способов:
Приведение корней с разными показателями
Для того, чтобы упростить выражение с корнями, которое содержит корни разных степеней, необходимо привести все корни к одной степени.
Например, есть квадратный корень (второй степени √ 2 ) и кубический корень (третьей степени 3 √ 3 ).
Во-первых, необходимо найти наименьшее общее кратное (НОК) для степеней. В нашем примере НОК=6 (2х3).
Во-вторых, применим свойство a = n √ a n : √ 2 = 2 √ 2 = 6 √ 2 3 = 6 √ 8 ; 3 √ 3 = 6 √ 3 2 = 6 √ 9
Получилось два корня одинаковой степени, с которыми можно совершать различные математические действия.
Корень: сложение и вычитание корней
Основное правила сложения и вычитания квадратных корней: сложение и вычитание квадратного корня возможны только при условии одинакового подкоренного выражения.
Примеры:
2√ 3 + 3√ 3 = 5√ 3
2√ 3 + 2√ 4 – не выполняется.
Алгоритм действия:
1. Упростить подкоренное выражение путем разложения на простые множители.
2. Затем нужно извлечь корень из квадратного числа и записать полученное значение перед знаком корня.
3. После процесса упрощения необходимо подчеркнуть корни с одинаковыми подкоренными выражениями — только их можно складывать и вычитать.
4. У корней с одинаковыми подкоренными выражениями необходимо сложить или вычесть множители, которые стоят перед знаком корня. Подкоренное выражение остается без изменений. Нельзя складывать или вычитать подкоренные числа!
Корень: умножение
Умножение корней без множителей
Произведение корней из чисел равно корню из произведения этих чисел.
√ a*b =√ a *√ b
Важно: между собой можно умножать только одинаковые степени корней, то есть можно умножить один квадратный корень на другой, но нельзя умножить квадратный корень на корень кубической степени.
Примеры:
√ 2 х √ 3 = √ 6
√ 6 х √ 3 = √ 18 = √ 3х3х2 = 3√ 2
Умножение корней с множителями
При умножении корней с множителями нужно отдельно перемножить множители и подкорневые выражения (числа). Подкорневые числа можно перемножать между собой только в том случае, если они имеют одинаковые степени (см. умножение корней без множителей). В случае отсутствия множителя, он равен единице.
Примеры:
3√ 2 х √ 5 = (3х1) √ (2*5) = 3√ 10
4√ 2 х 3√ 3 = (3х4) √ (2х3) = 12√ 6
Корень: деление
Основной правило деления — подкоренные выражения делятся на подкоренные выражения, а множители на множители.
√ a:b =√ a :√ b
В процессе деления квадратных корней дроби упрощаются.
Деление корней без множителей
Частное корней из чисел равно корню из частного этих чисел.
Важно: между собой можно делить только одинаковые степени корней, то есть можно делить один квадратный корень на другой, но нельзя делить квадратный корень на корень кубической степени.
Пример. √ 21 :√ 3 =√ 21:3 =√ 7
Деление квадратных корней с множителями
Примеры для практики
Чтобы попрактиковаться решать примеры на вычисление квадратный корней, можно скачать программу «Корни квадратные«
Как упростить алгебраическое выражение
Некоторые алгебраические примеры одним видом способны наводить ужас на школьников. Длинные выражения не только пугают, но и очень затрудняют вычисления. Пытаясь сходу понять, что и за чем следует, недолго запутаться. Именно по этой причине математики всегда стараются максимально упростить «жуткое» задание и только потом приступают к его решению. Как ни странно, такой трюк значительно ускоряет процесс работы.
Упрощение является одним из фундаментальных моментов в алгебре. Если в простых задачах без него ещё можно обойтись, то более трудные для вычисления примеры могут оказаться «не по зубам». Тут-то и пригодятся эти навыки! Тем более что сложных математических знаний не требуется: достаточно будет всего лишь запомнить и научиться применять на практике несколько базовых приёмов и формул.
Необходимые знания и умения
Вне зависимости от сложности вычислений при решении любого выражения важно соблюдать порядок выполнения операций с числами:
Последние два пункта можно спокойно поменять местами и это никак не отразится на результате. Но складывать два соседних числа, когда рядом с одним из них стоит знак умножения категорически нельзя! Ответ если и получится, то неверный. Поэтому нужно запомнить последовательность.
Применение подобных
К таким элементам относятся числа с переменной одного порядка или одинаковой степени. Существуют и так называемые свободные члены, не имеющие рядом с собой буквенного обозначения неизвестного.
Суть заключается в том, что при отсутствии скобок можно упростить выражение, складывая или вычитая между собой подобные.
Несколько наглядных примеров:
Разложение числа на множители
Эта маленькая математическая хитрость, если научиться её правильно использовать, в будущем не раз поможет справиться с каверзной задачкой. Да и понять, как работает «система», несложно: разложением называют произведение нескольких элементов, вычисление которого даёт исходное значение. Таким образом, 20 можно представить как на 20×1, 2×10, 5×4, 2×5×2 или другим способом.
На заметку: множители всегда совпадают с делителями. Так что искать рабочую «пару» для разложения нужно среди чисел, на которые исходное делится без остатка.
Проделывать такую операцию можно как со свободными членами, так и с цифрами при переменной. Главное, не потерять последнюю во время вычислений — даже после разложения неизвестная не может взять и «уйти в никуда». Она остаётся при одном из множителей:
Простые числа, которые можно разделить лишь на себя или 1, никогда не раскладываются — в этом нет смысла.
Основные способы упрощения
Первое, за что цепляется взгляд:
Алгебраические примеры в школьной программе часто составляются с учётом того, что их можно красиво упростить.
Вычисления в скобках
Внимательно следите за знаком, стоящим перед скобками! Умножение или деление применяется к каждому элементу внутри, а минус — меняет имеющиеся знаки «+» или «-» на противоположные.
Скобки вычисляются по правилам либо по формулам сокращённого умножения, после чего приводятся подобные.
Сокращение дробей
Сокращать дроби тоже несложно. Они сами через раз «охотно убегают», стоит произвести операции с приведением подобных членов. Но упростить пример можно ещё до этого: обращайте внимание на числитель и знаменатель. Они нередко содержат явные или скрытые элементы, которые можно взаимно сократить. Правда, если в первом случае нужно всего лишь вычеркнуть лишнее, во втором придётся подумать, приводя часть выражения к виду для упрощения. Используемые методы:
Когда выражение или его часть находится под корнем, первостепенная задача упрощения практически аналогична случаю с дробями. Необходимо искать способы полностью от него избавиться или, если это невозможно, максимально сократить мешающий вычислениям знак. Например, до ненавязчивого √(3) или √(7).
Верный способ упростить подкоренное выражение — попытаться разложить его на множители, часть из которых выносится за пределы знака. Наглядный пример: √(90)=√(9×10) =√(9)×√(10)=3√(10).
Другие маленькие хитрости и нюансы:
Упрощение степенного выражения
Если в случае простых вычислений на минус или плюс примеры упрощаются за счёт приведения подобных, то как быть при умножении или делении переменных с разными степенями? Их можно легко упростить, запомнив два основных момента:
Единственное условие для такого упрощения — одинаковое основание у обоих членов. Примеры для наглядности:
Отмечаем, что операции с числовыми значениями, стоящими перед переменными, происходят по обычным математическим правилам. И если присмотреться, то становится понятно, что степенные элементы выражения «работают» аналогично:
Как и в любом деле, при упрощении алгебраических выражений необходимо не только знание основ, но и практика. Уже через несколько занятий примеры, когда-то кажущиеся сложными, будут сокращаться без особого труда, превращаясь в короткие и легко решаемые.
Видео
Это видео поможет вам разобраться и запомнить, как упрощаются выражения.
Преобразования иррациональных выражений
Иррациональные выражения и их преобразования
Этот урок будет продолжением предыдущего и будет посвящён преобразованиям самых разных выражений, содержащих всевозможные корни. Такие выражения называются иррациональными. Здесь появятся и выражения с буквами, и дополнительные условия, и избавление от иррациональности в дробях, и некоторые продвинутые приёмы в работе с корнями. Те приёмы, которые будут рассматриваться в данном уроке, станут хорошей базой для решения задач ЕГЭ (и не только) практически любого уровня сложности. Итак, давайте приступим.
Прежде всего я продублирую здесь основные формулы и свойства корней. Чтобы не скакать из темы в тему. Вот они:
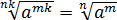
Формулы эти надо обязательно знать и уметь применять. Причём в обе стороны — как слева направо, так и справа налево. Именно на них и основывается решение большинства заданий с корнями любой степени сложности. Начнём пока с самого простого — с прямого применения формул или их комбинаций.
Простое применение формул
Вычислить:
Даже в таком простеньком примере возможны несколько путей к ответу.
Первый — просто перемножить корни по первому свойству и извлечь корень из результата:
Решать можно как больше нравится. В любом из вариантов ответ получается один — восьмёрка. Мне, например, проще перемножить 4 и 128 и получить 512, а из этого числа отлично извлекается кубический корень. Если кто-то не помнит, что 512 — это 8 в кубе, то не беда: можно записать 512 как 2 9 (первые 10 степеней двойки, я надеюсь, помните?) и по формуле корня из степени:
Вычислить: 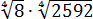
Если работать по первому свойству (всё загнать под один корень), то получится здоровенное число, из которого корень потом извлекать — тоже не сахар. Да и не факт, что он извлечётся ровно.) Поэтому здесь полезно в числе 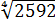
И теперь всё наладилось:
Осталось восьмёрку и двойку записать под одним корнем (по первому свойству) и — готово дело. 🙂
Добавим теперь немного дробей.
Пример совсем примитивный, однако и в нём имеются варианты. Можно с помощью вынесения множителя преобразовать числитель и сократить со знаменателем:
А можно сразу воспользоваться формулой деления корней:
Как видим, и так, и сяк — всяко правильно.) Если не споткнуться на полпути и не ошибиться. Хотя где тут ошибаться-то…
Разберём теперь самый последний пример из домашнего задания прошлого урока:
Совершенно немыслимый набор корней, да ещё и вложенных. Как быть? Главное — не бояться! Здесь мы первым делом замечаем под корнями числа 2, 4 и 32 — степени двойки. Первое что нужно сделать — привести все числа к двойкам: всё-таки чем больше одинаковых чисел в примере и меньше разных, тем проще.) Начнём отдельно с первого множителя:
Число 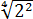
Теперь, согласно корню из произведения:
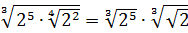
В числе 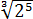
А с выражением 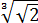
Значит, первый множитель запишется вот так:
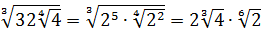
Вложенные корни исчезли, числа стали поменьше, что уже радует. Вот только корни разные, но пока так и оставим. Надо будет — преобразуем к одинаковым. Берёмся за второй множитель.)
Второй множитель преобразовываем аналогично, по формуле корня из произведения и корня из корня. Где надо — сокращаем показатели по пятой формуле:
Вставляем всё в исходный пример и получаем:
Получили произведение целой кучи совершенно разных корней. Неплохо было бы привести их все к одному показателю, а там — видно будет. Что ж, это вполне возможно. Наибольший из показателей корней равен 12, а все остальные — 2, 3, 4, 6 — делители числа 12. Поэтому будем приводить все корни по пятому свойству к одному показателю — к 12:
Считаем и получаем:
Красивого числа не получили, ну и ладно. Нас просили упростить выражение, а не посчитать. Упростили? Конечно! А вид ответа (целое число или нет) здесь уже не играет никакой роли.
Немного сложения / вычитания и формул сокращённого умножения
К сожалению, общих формул для сложения и вычитания корней в математике нету. Однако, в заданиях сплошь и рядом встречаются эти действия с корнями. Здесь необходимо понимать, что любые корни — это точно такие же математические значки, как и буквы в алгебре.) И к корням применимы те же самые приёмы и правила, что и к буквам — раскрытие скобок, приведение подобных, формулы сокращённого умножения и т.п.
Например, каждому ясно, что 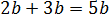
Если корни разные, то ищем способ сделать их одинаковыми — внесением/вынесением множителя или же по пятому свойству. Если ну никак не упрощается, то, возможно, преобразования более хитрые.
Смотрим первый пример.
Найти значение выражения: 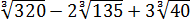
Все три корня хоть и кубические, но из разных чисел. Чисто не извлекаются и между собой складываются/вычитаются. Стало быть, применение общих формул здесь не катит. Как быть? А вынесем-ка множители в каждом корне. Хуже в любом случае не будет.) Тем более что других вариантов, собственно, и нету:
Стало быть, 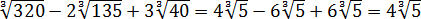
Вот и всё решение. Здесь мы от разных корней перешли к одинаковым с помощью вынесения множителя из-под корня. А затем просто привели подобные.) Решаем дальше.
Найти значение выражения:
С корнем из семнадцати точно ничего не поделаешь. Работаем по первому свойству — делаем из произведения двух корней один корень:
А теперь присмотримся повнимательнее. Что у нас под большим кубическим корнем? Разность ква.. Ну, конечно! Разность квадратов:
Теперь осталось только извлечь корень: 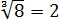
Дальше очень похожий пример, но посложнее.
Вычислить:
Здесь придётся проявить математическую смекалку.) Мыслим примерно следующим образом: «Так, в примере произведение корней. Под одним корнем разность, а под другим — сумма. Очень похоже на формулу разности квадратов. Но… Корни — разные! Первый квадратный, а второй — четвёртой степени… Хорошо бы сделать их одинаковыми. По пятому свойству можно легко из квадратного корня сделать корень четвёртой степени. Для этого достаточно подкоренное выражение возвести в квадрат.»
Если вы мыслили примерно так же, то вы — на полпути к успеху. Совершенно верно! Превратим первый множитель в корень четвёртой степени. Вот так:
Теперь, ничего не поделать, но придётся вспомнить формулу квадрата разности. Только в применении к корням. Ну и что? Чем корни хуже других чисел или выражений?! Возводим:
«Хм, ну возвели и что? Хрен редьки не слаще. Стоп! А если вынести четвёрку под корнем? Тогда выплывет то же самое выражение, что и под вторым корнем, только с минусом, а ведь именно этого мы и добиваемся!»
Верно! Выносим четвёрку:
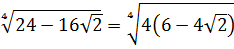
А теперь — дело техники:
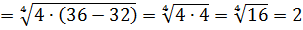
Вот так распутываются сложные примеры. ) Теперь пора потренироваться с дробями.
Ясно, что надо преобразовывать числитель. Как? По формуле квадрата суммы, разумеется. У нас есть ещё варианты разве? 🙂 Возводим в квадрат, выносим множители, сокращаем показатели (где надо):
Во как! Получили в точности знаменатель нашей дроби. ) Значит, вся дробь, очевидно, равна единице:
Ещё пример. Только теперь на другую формулу сокращённого умножения.)
Выносим множители из-под корней:
Следовательно,
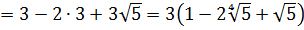
Теперь всё нехорошее великолепно сокращается и получается:
Что ж, поднимаемся на следующий уровень. 🙂
Буквы и дополнительные условия
Буквенные выражения с корнями — штука более хитрая, чем числовые выражения, и является неиссякаемым источником досадных и очень грубых ошибок. Перекроем этот источник.) Ошибки всплывают из-за того, что частенько таких заданиях фигурируют отрицательные числа и выражения. Они либо даны нам прямо в задании, либо спрятаны в буквах и дополнительных условиях. А нам в процессе работы с корнями постоянно надо помнить, что в корнях чётной степени как под самим корнем, так и в результате извлечения корня должно быть неотрицательное выражение. Ключевой формулой в задачах этого пункта будет четвёртая формула:
С корнями нечётной степени вопросов никаких — там всегда всё извлекается что с плюсом, что с минусом. И минус, если что, выносится вперёд. Будем сразу разбираться с корнями чётных степеней.) Например, такое коротенькое задание.
Упростить: 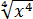
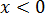
Казалось бы, всё просто. Получится просто икс. ) Но зачем же тогда дополнительное условие 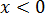
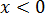
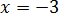
Что мы видим? На входе было отрицательное число, а на выходе — уже положительное. Было минус три, стало плюс три.) Возвращаемся к буквам. Вне всяких сомнений, по модулю это будет точно икс, но только сам икс у нас с минусом (по условию!), а результат извлечения (в силу арифметического корня!) должен быть с плюсом. Как получить плюс? Очень просто! Для этого достаточно перед заведомо отрицательным числом поставить минус.) И правильное решение выглядит так:
Кстати сказать, если бы мы воспользовались формулой 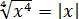
Вынести множитель за знак корня: 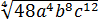
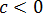
Первый взгляд — на подкоренное выражение. Тут всё ОК. При любом раскладе оно будет неотрицательным. Начинаем извлекать. По формуле корня из произведения, извлекаем корень из каждого множителя:
Откуда взялись модули, объяснять, думаю, уже не надо.) А теперь анализируем каждый из модулей.
А теперь — обратная задача. Не самая простая, сразу предупреждаю!
Внести множитель под знак корня: 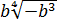
Если вы сразу запишете решение вот так
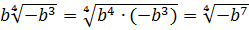
то вы попали в ловушку. Это неверное решение! В чём же дело?
Давайте вглядимся в выражение под корнем 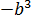
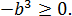
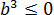
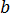
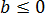
И ошибка здесь состоит в том, что мы вносим под корень неположительное число 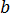
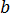
И теперь уже неотрицательное число (-b) спокойно вносим под корень по всем правилам:
Этот пример наглядно показывает, что, в отличие от других разделов математики, в корнях правильный ответ далеко не всегда вытекает автоматически из формул. Необходимо подумать и лично принять верное решение.) Особенно следует быть внимательнее со знаками в иррациональных уравнениях и неравенствах.
Разбираемся со следующим важным приёмом в работе с корнями — избавлением от иррациональности.
Избавление от иррациональности в дробях
Если в выражении присутствуют корни, то, напомню, такое выражение называется выражением с иррациональностью. В некоторых случаях бывает полезно от этой самой иррациональности (т.е. корней) избавиться. Как можно ликвидировать корень? Корень у нас пропадает при… возведении в степень. С показателем либо равным показателю корня, либо кратным ему. Но, если мы возведём корень в степень (т.е. помножим корень сам на себя нужное число раз), то выражение от этого поменяется. Нехорошо.) Однако в математике бывают темы, где умножение вполне себе безболезненно. В дробях, к примеру. Согласно основному свойству дроби, если числитель и знаменатель умножить (разделить) на одно и то же число, то значение дроби не изменится.
Допустим, нам дана вот такая дробь:
Можно ли избавиться от корня в знаменателе? Можно! Для этого корень надо возвести в куб. Чего нам не хватает в знаменателе для полного куба? Нам не хватает множителя 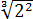
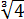
Корень в знаменателе исчез. Но… он появился в числителе. Ничего не поделать, такова судьба.) Нам это уже не важно: нас просили знаменатель от корней освободить. Освободили? Безусловно.)
Кстати, те, кто уже в ладах с тригонометрией, возможно, обращали внимание на то, что в некоторых учебниках и таблицах, к примеру, 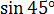
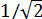
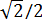
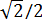
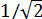
Зачем нам освобождаться от иррациональности в дробях? Какая разница — в числителе корень сидит или в знаменателе? Калькулятор всё равно всё посчитает.) Ну, для тех, кто не расстаётся с калькулятором, разницы действительно практически никакой… Но, даже считая на калькуляторе, можно обратить внимание на то, что делить на целое число всегда удобнее и быстрее, чем на иррациональное. А уж про деление в столбик вообще умолчу.)
Следующий пример только подтвердит мои слова.
Освободиться от иррациональности в знаменателе дроби:
Как здесь ликвидировать квадратный корень в знаменателе? Если числитель и знаменатель помножить на выражение 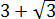
Такое выражение, которое при домножении какой-то суммы (или разности) выводит на разность квадратов, ещё называют сопряжённым выражением. В нашем примере сопряжённым выражением будет служить разность 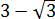
Что тут можно сказать? В результате наших манипуляций не то что корень из знаменателя исчез — вообще дробь исчезла! 🙂 Даже с калькулятором отнять корень из трёх от тройки проще, чем считать дробь с корнем в знаменателе. Ещё пример.
Освободиться от иррациональности в знаменателе дроби:
Как здесь выкручиваться? Формулы сокращённого умножения с квадратами сразу не катят — не получится полной ликвидации корней из-за того, что корень у нас в этот раз не квадратный, а кубический. Надо, чтобы корень как-то возвёлся в куб. Стало быть, применять надо какую-то из формул с кубами. Какую? Давайте подумаем. В знаменателе — сумма 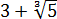
В качестве a у нас тройка, а в качестве b — корень кубический из пяти:
И снова дробь исчезла.) Такие ситуации, когда при освобождении от иррациональности в знаменателе дроби у нас вместе с корнями полностью исчезает сама дробь, встречаются очень часто. Как вам вот такой примерчик!
Попробуйте просто сложить эти три дроби! Без ошибок! 🙂 Один общий знаменатель чего стоит. А что, если попробовать освободиться от иррациональности в знаменателе каждой дроби? Что ж, пробуем:
Ух ты, как интересно! Все дроби пропали! Напрочь. И теперь пример решается в два счёта:
Просто и элегантно. И без долгих и утомительных вычислений. 🙂
Именно поэтому операцию освобождения от иррациональности в дробях надо уметь делать. В подобных навороченных примерах только она и спасает, да.) Разумеется, внимательность никто не отменял. Бывают задания, где просят избавиться от иррациональности в числителе. Эти задания ничем от рассмотренных не отличаются, только от корней очищается числитель.)
Более сложные примеры
Осталось рассмотреть некоторые специальные приёмы в работе с корнями и потренироваться распутывать не самые простые примеры. И тогда полученной информации уже будет достаточно для решения заданий с корнями любого уровня сложности. Итак — вперёд.) Для начала разберёмся, что делать со вложенными корнями, когда формула корня из корня не работает. Например, вот такой примерчик.
Вычислить:
Корень под корнем… К тому же под корнями сумма или разность. Стало быть, формула корня из корня (с перемножением показателей) здесь не действует. Значит, надо что-то делать с подкоренными выражениями: у нас просто нету других вариантов. В таких примерах чаще всего под большим корнем зашифрован полный квадрат какой-нибудь суммы. Или разности. А корень из квадрата уже отлично извлекается! И теперь наша задача — его расшифровать.) Такая расшифровка красиво делается через систему уравнений. Сейчас всё сами увидите.)
Итак, под первым корнем у нас вот такое выражение:
А вдруг, не угадали? Проверим! Возводим в квадрат по формуле квадрата суммы:
Всё верно.) Но… Откуда я взял это выражение 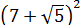
Нет.) Мы его чуть ниже получим честно. Просто по данному выражению я показываю, как именно составители заданий шифруют такие квадраты. 🙂 Что такое 54? Это сумма квадратов первого и второго чисел. Причём, обратите внимание, уже без корней! А корень остаётся в удвоенном произведении, которое в нашем случае равно 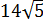
Теперь удвоенное произведение. Оно у нас 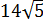
Получили вот такую системку:
Решаем обычным методом подстановки. Выражаем из второго уравнения, например, и подставляем в первое:
Решим первое уравнение:
И тут вопрос — а какое из решений нам подходит? Давайте подумаем. Отрицательные решения можно сразу отбросить: при возведении в квадрат минусы «сгорят», и всё подкоренное выражение в целом не изменится.) Остаются первые два варианта. Выбрать их можно совершенно произвольно: от перестановки слагаемых сумма всё равно не меняется.) Пусть, например, 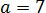
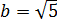
Итого получили под корнем квадрат вот такой суммы:
Я не зря так детально описываю ход решения. Чтобы было понятно, как происходит расшифровка.) Но есть одна проблемка. Аналитический способ расшифровки хоть и надёжный, но весьма длинный и громоздкий: приходится решать биквадратное уравнение, получать четыре решения системы и потом ещё думать, какие из них выбрать… Хлопотно? Согласен, хлопотно. Этот способ безотказно работает в большинстве подобных примеров. Однако очень часто можно здорово сократить себе работу и найти оба числа творчески. Подбором.) Да-да! Сейчас, на примере второго слагаемого (второго корня), я покажу более лёгкий и быстрый способ выделения полного квадрата под корнем.
Итак, теперь у нас вот такой корень: 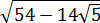
Получилось! Значит, наше подкоренное выражение — это на самом деле квадрат разности:
Вот такой вот способ-лайт, чтобы не связываться с системой. Не всегда работает, но во многих таких примерах его вполне достаточно. Итак, под корнями — полные квадраты. Осталось только правильно извлечь корни, да досчитать пример:
А теперь разберём ещё более нестандартное задание на корни.)
Докажите, что число A – целое, если 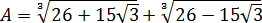
Впрямую ничего не извлекается, корни вложенные, да ещё и разных степеней… Кошмар! Однако, задание имеет смысл.) Стало быть, ключ к его решению имеется.) А ключ здесь такой. Рассмотрим наше равенство
как уравнение относительно A. Да-да! Хорошо бы избавиться от корней. Корни у нас кубические, поэтому возведём-ка обе части равенства в куб. По формуле куба суммы:
Кубы и корни кубические друг друга компенсируют, а под каждым большим корнем забираем одну скобку у квадрата и сворачиваем произведение разности и суммы в разность квадратов:
Отдельно сосчитаем разность квадратов под корнями:
Отлично! Значит, всё наше равенство ещё сильнее упростится:
А теперь делаем финт ушами — заменяем сумму корней в скобках на A (согласно условию примера!).
Получаем кубическое уравнение 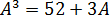
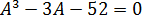
Здесь как раз тот случай, когда один из корней легко угадывается — это 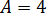
Как разложить? Либо по схеме Горнера, либо делением «уголком» на скобку (A-4), либо даже группировкой (если представить -3A как -16A+13A). Объяснять подробно деление уголком или схему Горнера в теме про корни — уже совсем отклоняться от курса.) Кто в теме — и так поймёт.
А теперь легко заметить, что квадратный трёхчлен во вторых скобках имеет отрицательный дискриминант, а значит, наше уравнение имеет единственный действительный корень 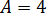
А теперь — поупрощаем некоторые дробные выражения с корнями. От простого — к сложному. Здесь всё точно так же, как и с многочленами. Только в применении к корням.) Я же говорил, что действия с корнями ничем не отличаются от таковых с буквами. И к корням с таким же успехом применима вся алгебра седьмого класса — формулы сокращённого умножения, разложение на множители, приведение подобных и т.п.
Например, такое задание.
Пример явно намекает на применение формулы разности квадратов:
Спрашивается, а где же здесь квадраты? Сплошные корни… Сейчас покажу. 🙂
Берём числитель нашей дробушки: 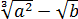
Что такое 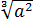
Хорошо, а из 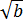
По такой технологии, между прочим, можно совершенно любой корень превратить в совершенно любую степень. Какую хотим. 🙂 Как, например, 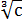
Хотим из степеней корни делаем, хотим — наоборот, степени из корней. Что хотим, то и творим. Математика, однако! 🙂
Итак, весь наш числитель можно представить как разность квадратов:
А дальше никаких проблем — раскладываем числитель на множители и сокращаем:
Действуем аналогично. Раскладываем на множители и сокращаем. 🙂 В числителе применяем группировку. Например, вот такую:
А в знаменателе просто выносим общий множитель 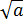
Подставляем всё в нашу дробь и сокращаем:
Как видим, разложение на множители очень популярно в теме с корнями. Очень! И особенно — формула разности квадратов. Именно поэтому формулы сокращённого умножения так важно знать и уметь применять. 🙂
Ну и на десерт распутаем что-нибудь навороченное. )
Чтобы не запутаться и не наляпать ошибок, будем действовать по порядку. При взгляде на любой пример всегда задаём сами себе вопрос: «Что в примере мне больше всего не нравится?» В данном примере большинство скажет: «Числитель первой дроби!» Верно! Вот и упростим его отдельно: остальная часть примера от этого никак не пострадает.) Итак,
Вместо знака деления удобно использовать черту дроби. Вот так:
Сначала упростим дробь. Как? Попробуем сократить.) Для этого, ясное дело, надо разложить на множители числитель и знаменатель, да… Берём отдельно числитель 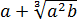
Если теперь подставить вместо a выражение 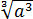
Со знаменателем полная аналогия:
Теперь от упрощённой дроби отнимаем единичку. Как? Делаем из единички дробь и — вперёд!
Следующим пунктом идёт деление полученной дроби на выражение 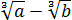
Уфф… Дальше… Отнимаем от полученного выражения дробь 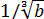
И, наконец, последнее усилие. Возводим результат в куб:
Ну как, всё понятно? Тогда — вперёд, набиваем руку и делаем примеры!
Освободиться от иррациональности в знаменателе дробей:
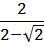
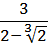
Вычислить:
Доказать, что A – целое число, если 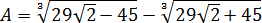
Ответы (пока) давать не буду — иначе неинтересно. 🙂 До встречи и успехов!