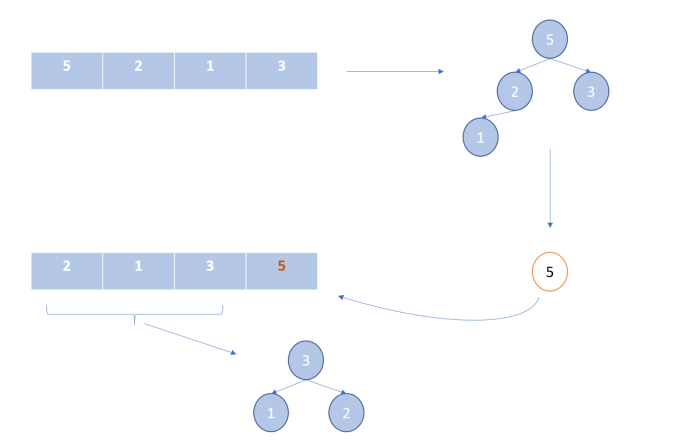
Как упорядочить множество python
Алгоритмы сортировки на Python
В этой статье мы вкратце расскажем, какие есть основные алгоритмы сортировки и каковы их главные характеристики. Также по каждому алгоритму покажем реализацию на Python.
Искусство наведения порядка
Сортировка означает размещение элементов в определенном порядке. Этот конкретный порядок определяется свойством сравнения элементов. В случае целых чисел мы говорим, что сначала идет меньшее число, а потом — большее.
Расположение элементов в определенном порядке улучшает поиск элемента. Следовательно, сортировка широко используется в информатике.
В данной статье мы рассмотрим обычные алгоритмы сортировки и их реализации на Python. Для сравнения их производительности мы будем рассматривать задачу с сайта Leetcode о сортировке массива. Размеры данных этой задачи ограничены следующим образом:
Мы решили эту задачу при помощи всех известных алгоритмов сортировки. Вот какие у нас получились результаты:
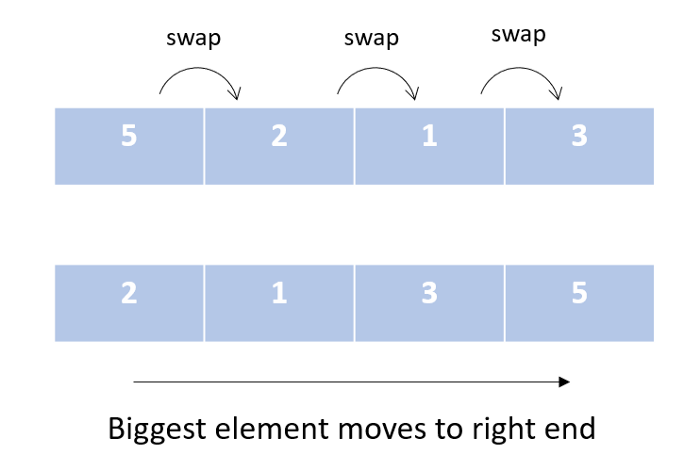
Сортировка методом пузырька
Это самый простой алгоритм сортировки. В процессе его выполнения мы перебираем наш список и на каждой итерации сравниваем элементы попарно. При необходимости элементы меняются местами, чтобы больший элемент отправлялся в конец списка.
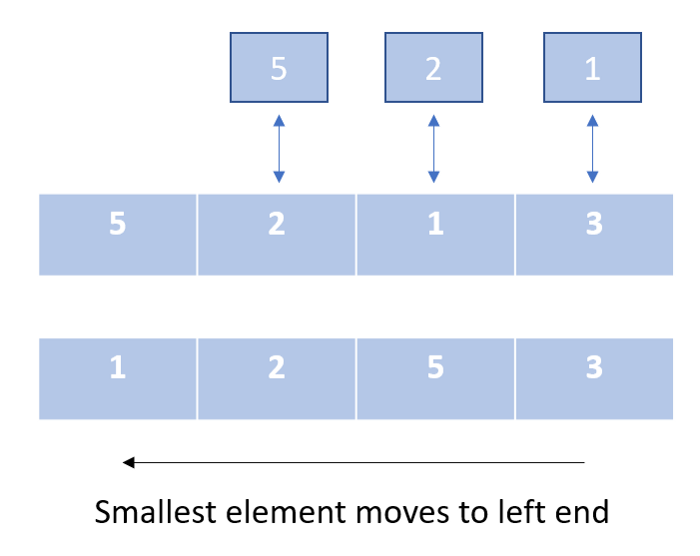
Сортировка выбором
В этом алгоритме мы создаем два сегмента нашего списка: один отсортированный, а другой несортированный.
В процессе выполнения алгоритма мы каждый раз удаляем самый маленький элемент из несортированного сегмента списка и добавляем его в отсортированный сегмент. Мы не меняем местами промежуточные элементы. Следовательно, этот алгоритм сортирует массив с минимальным количеством перестановок.
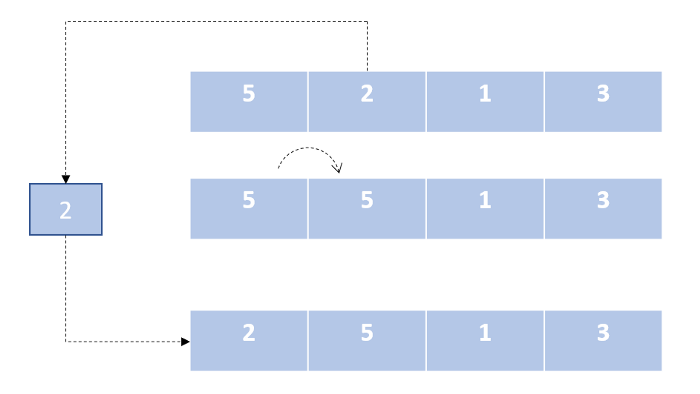
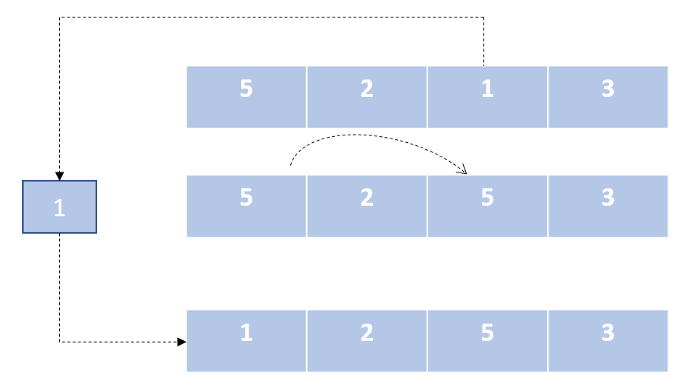
Сортировка вставками
Подобно алгоритму сортировки выбором, мы делим наш список на две части. Далее мы перебираем неотсортированную часть и вставляем каждый элемент из данного сегмента на его правильное место в отсортированной части списка.
Марк Лутц «Изучаем Python»
Скачивайте книгу у нас в телеграм
Сортировка Шелла
Сортировка Шелла является оптимизированным вариантом сортировки вставками.
Оптимизация достигается путем сравнения не только соседних элементов, но и элементов на определенном расстоянии, которое в течении работы алгоритма уменьшается. На последней итерации это расстояние равно 1. После этого алгоритм становится обычным алгоритмом сортировки вставками, что гарантирует правильный результат сортировки.
Но следует отметить один момент: к тому времени, когда это произойдет, наш массив будет почти отсортирован, поэтому итерации будут выполнятся очень быстро.
Пирамидальная сортировка («сортировка кучей»)
Как и в двух предыдущих алгоритмах, мы создаем два сегмента списка: отсортированный и несортированный.
В данном алгоритме для эффективного нахождения максимального элемента в неотсортированной части списка мы используем структуру данных «куча».
Метод heapify в примере кода использует рекурсию для получения элемента с максимальным значением на вершине.
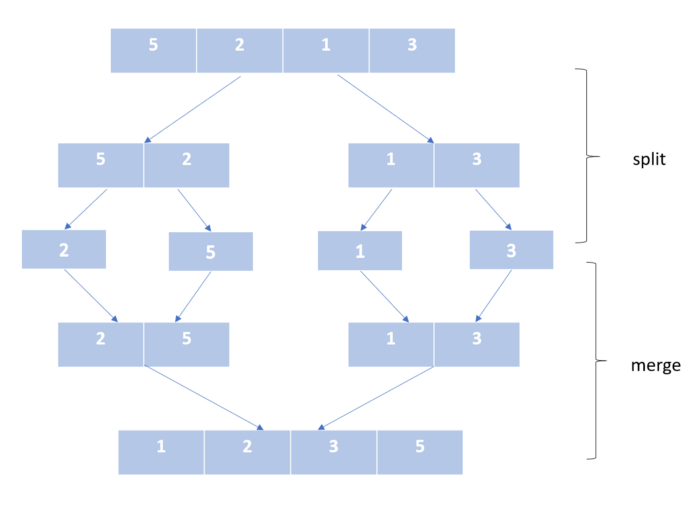
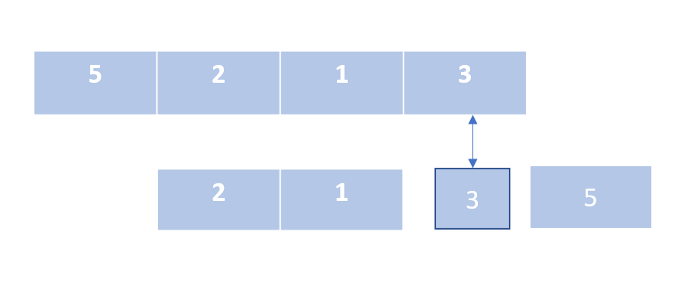
Сортировка слиянием
Этот алгоритм работает по принципу «разделяй и властвуй».
Здесь мы делим список ровно пополам и продолжаем это делать, пока в нем не останется только один элемент. Затем мы объединяем уже упорядоченные части нашего списка. Мы продолжаем это делать, пока не получим отсортированный список со всеми элементами несортированного входного списка.
Быстрая сортировка
В этом алгоритме мы разбиваем список при помощи опорного элемента, сортируя значения вокруг него.
В нашей реализации мы выбрали опорным элементом последний элемент массива. Наилучшая производительность достигается тогда, когда опорный элемент делит список примерно пополам.
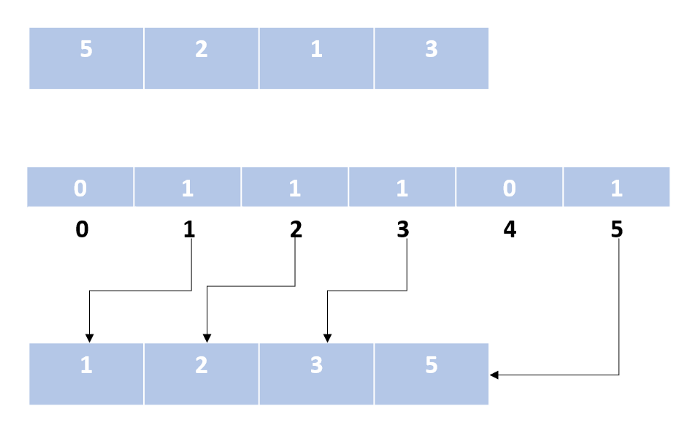
Сортировка подсчетом
Этот алгоритм не производит сравнение элементов. Для сортировки используются математические свойства целых чисел. Мы подсчитываем вхождения числа в массиве и сохраняем результат во вспомогательном массиве, где индексу соответствует значение ключа.
Следует также упомянуть поразрядную сортировку, которая использует сортировку подсчетом либо блочную (корзинную) сортировку в качестве подпрограммы. Этот метод сортировки заслуживает отдельной статьи для разбора.
Для удобства соберем весь наш код вместе:
Мы нашли потрясающий плейлист, в котором алгоритмы сортировки демонстрируются при помощи народного танца. Посмотрите это видео, оно того стоит!
В нашем небольшом исследовании мы изучили различные алгоритмы сортировки и определили время их выполнения, а также их потребности в памяти. Теперь мы понимаем, что значит время выполнения, стабильность алгоритма и используемая память. Чтобы выбрать подходящий алгоритм, мы должны оценивать эти параметры. Также, для создания более эффективных решений, типа Timsort, мы можем комбинировать наши базовые алгоритмы.
Множества в Python
Множества (set) в Python — это встроенный тип, предлагающий широкий набор возможностей, которые повторяют теорию множеств из математики. Тем не менее интерпретация может отличаться от той, что принята в математике. Set импортировать не нужно. А в этом материале вы узнаете о нем все, что потребуется для работы.
Что это
Множества — это неупорядоченная коллекция уникальных элементов, сгруппированных под одним именем. Множество может быть неоднородным — включать элементы разных типов. Множество всегда состоит только из уникальных элементов (дубли запрещены) в отличие от списков и кортежей в Python. Объект set — это также коллекция уникальных хэшируемых объектов. Объект называется хэшируемым в том случае, если его значение хэша не меняется. Это используется в ключах словарей и элементах множеств, ведь значения хэшей применяются в их внутренних структурах.
Чаще всего множества в Python используются для проверки на принадлежность, удаления повторов из последовательности и выполнения математических операций, таких как пересечение, объединение, поиск разностей и симметрических разностей. Изображение ниже показывает два примера множеств (алфавит и цифры), каждый из которых включает уникальные неизменяемые объекты.
Создание множеств Python
Создать объект set в Python можно двумя путями:
Примечание: не используйте зарезервированные ключевые слова и названия встроенных классов в качестве имен для множеств. Это не поощряется в программировании на Python.
Первый способ (с использованием фигурных скобок <> ) определенно проще.
Добавление элементов в множества Python
Добавление одного элемента в множество Python
Добавление нескольких элементов в множество Python
Удаление элементов из множеств Python
Один или несколько элементов можно удалить из объекта set с помощью следующих методов. Их отличие в виде возвращаемого значения.
remove()
Метод remove() полезен в тех случаях, когда нужно удалить из множества конкретный элемент и вернуть ошибку в том случае, если его нет в объекте.
Следующий код показывает метод remove() в действии.
discard()
Метод discard() полезен, потому что он удаляет конкретный элемент и не возвращает ошибку, если тот не был найден во множестве.
Метод pop() удаляет по одному элементу за раз в случайном порядке. Set — это неупорядоченная коллекция, поэтому pop() не требует аргументов (индексов в этом случае). Метод pop() можно воспринимать как неконтролируемый способ удаления элементов по одному из множеств в Python.
Методы множеств Python
Вот что выдаст функция для объекта set в Python.
Часто используемые функции множеств Python
Вот на какие также стоит обратить внимание.
Функция принадлежности (членства)
Она проверяет на наличие конкретного элемента в множестве.
Разные функции
copy() — создает копию существующего множества и сохраняет ее в новом объекте.
clear() —очищает множество (удаляет все элементы за раз)
del — удаляет множество целиком
Операции множеств в Python
В этом разделе вы узнаете о разных операциях над множествами, которые являются частью теории множеств.
Объединение множеств
Пересечение множеств
Разность множеств
Симметричная разность множеств
Подмножество и надмножество в Python
Бонус
А теперь бонус для тех, кто дочитал до этого места. Многие начинающие программисты задаются вопросом, как удалить повторяющиеся элементы из списка?
Выводы
В поисках упорядоченного множества в Python: разбираемся с теорией и выбираем лучшую реализацию
Стандартный Set
Но хэш-таблица не позволяет выполнить операцию count_lower или подобные, поэтому придётся использовать другие структуры данных.
Что есть в других языках
Она реализована с помощью красно-чёрных деревьев. Смысл этой струкруты в том, что все элементы образуют собой двоичное дерево поиска, которое балансируется так, чтобы высота не превышала логарифм. Нам это даёт возможность с помощью одного спуска по дереву выполнить необходимые операции. Также с этой задачей может справиться Декартово дерево (Дерамида) по неявному ключу или AVL дерево.
Таким образом, целью этой статьи станет поиск аналога этой структуры в Python.
Как будем тестировать скорость работы структур данных
Для оценки времени работы я написал программу, которая будет выполнять последовательно несколько типов операций:
SortedSet.sorted_set.SortedSet
Пакет с многообещающим названием. Используем pip install sortedset
К сожалению, автор не приготовил нам функцию add и erase в каком-либо варианте, поэтому будем использовать объединение и вычитание множеств
Протестируем пока на множествах размера 10’000:
| Задача | Время работы |
|---|---|
| Добавление | 16.413 |
| Проверка на наличие | 0.018 |
| Цикл по всем элементам | 0.001 |
| Получение индексов | 0.008 |
| Получение значений по индексам | 0.015 |
| Удаление | 30.548 |
Как так получилось? Давайте загляем в исходный код:
Как оказалось, это обычный массив, в котором наличие элемента определяется бинпоиском. Это действительно отсортированное множество, но очень ленивое.
Вывод: почти бесполезно, несколько строчек кода завернули в класс
sortedcontainers.SortedSet
| Задача | Время работы |
|---|---|
| Добавление | 3.924 |
| Проверка на наличие | 1.198 |
| Цикл по всем элементам | 0.162 |
| Получение индексов | 3.959 |
| Получение значений по индексам | 4.909 |
| Удаление | 2.933 |
Но, не смотря на это, кажется мы нашли то, что искали! Все операции выполняются за приличное время. По сравнению с ordered_set некоторые операции выполняются дольше, но зато операция discard выполняется не за o(n), что очень важно для возможности использования этой структуры.
И как же оно работает?
На странице пакета мы можем прочитать, что реализована структура не так, как мы предполагали в начале статьи.
Если говорить кратко, то принцип действия похож на корневую оптимизацию.
Проблема с ordered_set
Bintrees
pip install bintrees
| Задача | AVLTree | FastAVLTree | RBTree | FastRBTree | BinaryTree | FastBinaryTree |
|---|---|---|---|---|---|---|
| Добавление | 21.946 | 2.285 | 20.486 | 2.373 | 11.054 | 2.266 |
| Проверка на наличие | 5.86 | 2.821 | 6.172 | 2.802 | 6.775 | 3.018 |
| Цикл по всем элементам | 0.935 | 0.297 | 0.972 | 0.302 | 0.985 | 0.295 |
| Удаление | 12.835 | 1.509 | 25.803 | 1.895 | 7.903 | 1.588 |
Результаты тестирования отчётливо показывают нам, почему использовать деревья поиска на Python — плохая идея в плане производительности. А вот в интеграции с Cython всё становится намного лучше.
| Задача | SortedSet | FastAVLTree |
|---|---|---|
| Добавление | 3.924 | 2.285 |
| Проверка на наличие | 1.198 | 2.821 |
| Цикл по всем элементам | 0.162 | 0.297 |
| Получение индексов | 3.959 | n/a |
| Получение значений по индексам | 4.909 | n/a |
| Удаление | 2.933 | 1.509 |
Что же выбрать
Можно ли сделать что-то быстрее
Облачные VPS серверы от Маклауд быстрые и безопасные.
Зарегистрируйтесь по ссылке выше или кликнув на баннер и получите 10% скидку на первый месяц аренды сервера любой конфигурации!
Всё о сортировке в Python: исчерпывающий гайд
Примечание Вы читаете улучшенную версию некогда выпущенной нами статьи.
Основы сортировки
Прим.перев. В Python вернуть None и не вернуть ничего — одно и то же.
Ещё одно отличие заключается в том, что метод list.sort() определён только для списков, в то время как sorted() работает со всеми итерируемыми объектами:
Прим.перев. При итерировании по словарю Python возвращает его ключи. Если вам нужны их значения или пары «ключ-значение», используйте методы dict.values() и dict.items() соответственно.
Рассмотрим основные функции сортировки Python.
Функции-ключи
С версии Python 2.4 у list.sort() и sorted() появился параметр key для указания функции, которая будет вызываться на каждом элементе до сравнения. Вот регистронезависимое сравнение строк:
Значение key должно быть функцией, принимающей один аргумент и возвращающей ключ для сортировки. Работает быстро, потому что функция-ключ вызывается один раз для каждого элемента.
Часто можно встретить код, где сложный объект сортируется по одному из его индексов. Например:
Тот же метод работает для объектов с именованными атрибутами:
Функции модуля operator
Функции operator дают возможность использовать множественные уровни сортировки в Python. Отсортируем учеников сначала по оценке, а затем по возрасту:
Используем функцию methodcaller() для сортировки учеников по взвешенной оценке:
Сортировка по возрастанию и сортировка по убыванию в Python
Стабильность сортировки и сложные сортировки в Python
Начиная с версии Python 2.2, сортировки гарантированно стабильны: если у нескольких записей есть одинаковые ключи, их порядок останется прежним. Пример:
Обратите внимание, что две записи с ‘blue’ сохранили начальный порядок. Это свойство позволяет составлять сложные сортировки путём постепенных сортировок. Далее мы сортируем данные учеников сначала по возрасту в порядке возрастания, а затем по оценкам в убывающем порядке, чтобы получить данные, отсортированные в первую очередь по оценке и во вторую — по возрасту:
Алгоритмы сортировки Python вроде Timsort проводят множественные сортировки так эффективно, потому что может извлечь пользу из любого порядка, уже присутствующего в наборе данных.
Декорируем-сортируем-раздекорируем
Вот так можно отсортировать данные учеников по оценке:
Это работает из-за того, что кортежи сравниваются лексикографически, сравниваются первые элементы, а если они совпадают, то сравниваются вторые и так далее.
Не всегда обязательно включать индекс в декорируемый список, но у него есть преимущества:
Ещё эта идиома называется преобразованием Шварца в честь Рэндела Шварца, который популяризировал её среди Perl-программистов.
Для больших списков и версий Python ниже 2.4, «декорируем-сортируем-раздекорируем» будет оптимальным способом сортировки. Для версий 2.4+ ту же функциональность предоставляют функции-ключи.
Использование параметра cmp
Все версии Python 2.x поддерживали параметр cmp для обработки пользовательских функций сравнения. В Python 3.0 от этого параметра полностью избавились. В Python 2.x в sort() можно было передать функцию, которая использовалась бы для сравнения элементов. Она должна принимать два аргумента и возвращать отрицательное значение для случая «меньше чем», положительное — для «больше чем» и ноль, если они равны:
Можно сравнивать в обратном порядке:
При портировании кода с версии 2.x на 3.x может возникнуть ситуация, когда нужно преобразовать пользовательскую функцию для сравнения в функцию-ключ. Следующая обёртка упрощает эту задачу:
Чтобы произвести преобразование, оберните старую функцию:
В Python 2.7 функция cmp_to_key() была добавлена в модуль functools.
Поддержание порядка сортировки
Прочее
Для сортировки с учётом языка используйте locale.strxfrm() в качестве ключевой функции или locale.strcoll() в качестве функции сравнения. Параметр reverse всё ещё сохраняет стабильность сортировки. Этот эффект можно сымитировать без параметра, использовав встроенную функцию reversed() дважды:
Чтобы создать стандартный порядок сортировки для класса, просто добавьте реализацию соответствующих методов сравнения:
Множества в Python (set, frozenset)
Множество — интуитивно понятный математический термин, который часто используется в обыденной речи и означает набор или совокупность неких элементов, что обладают каким-то общим свойством.
Не слишком строгое определение множества, однако, с ним возникали проблемы даже у великих математиков.
В широком смысле, элементами множеств могут быть даже нематериальные вещи: чётные числа, несданные задачи по термодинамике, алгоритмы сортировки, любимые фильмы Юлии и Алексея и даже мысли об эклерах.
🐱 Возьмите в руки кота. Взяли? Хорошо. Теперь множество котов в ваших руках насчитывает ровно один мурлыкающий элемент. Если же пушистику вдруг не понравится, что вы его тискаете, и он выскочит из рук, то элементов внутри множества не останется. Множество, в котором нет ни одного элемента, называется пустым. Но что же там в Python?
Назначение в Python
Множества (set) в питоне появились не сразу, и здесь они представлены как неупорядоченные коллекции уникальных и неизменяемых объектов. Коллекции, которые не являются ни последовательностями (как списки), ни отображениями (как словари). Хотя с последними у множеств много общего.
Можно сказать, что set напоминает словарь, в котором ключи не имеют соответствующих им значений
Пример set-ов в Python:
# множество натуральных чисел от 1 до 10 natural_num_set = <1, 2, 3, 4, 5, 6, 7, 8, 9, 10># множество персонажей Братства Кольца the_fellowship_of_the_ring_set = <'Гэндальф', 'Арагорн', 'Фродо', 'Сэм', 'Боромир', 'Леголас', 'Гимли', 'Мерри', 'Пиппин'># множество приближений math.sqrt(2) sqrt_approximation_set = <1.4142135623, 1.414213562, 1.41421356, 1.4142135, 1.414213># множество результатов какого-то голосования vote_result_set =
Особенности set
Одно из основных свойств множеств заключается в уникальности каждого из их элементов. Посмотрим, что получится, если сформировать set из строчки с заведомо повторяющимися символами:
strange_app = set(‘TikTok’) print(strange_app) >
Из результата были удалены дублирующиеся в слове ‘TikTok’ символы. Так множества в очередной раз доказали, что содержат в себе только уникальные элементы.
👉 Немаловажным является и тот факт, что при литеральном объявлении, итерируемые объекты сохраняют свою структуру.
pangram_second = set(‘съешь же ещё этих мягких французских булок, да выпей чаю’) print(pangram_ second) # попить чаю с функцией set(), к сожалению, не выйдет >
Отдельное python множество может включать в себя объекты разных типов:
Здесь нет никакого противоречия с математической дефиницией, так как все составляющие we_are_the_py_objects имеют вполне конкретное общее свойство, являясь объектами языка Питон.
Но не стоит забывать и внутреннее определение set-ов. Важно помнить, что list-ы и dict-ы не подходят на роль элементов множества, из-за своей изменяемой природы.
glados = <['Great cake']>print(glados) > Traceback (most recent call last): glados = <['Great cake']>TypeError: unhashable type: ‘list’
# словарь будет преобразован во множество его ключей, значения отбрасываются some_dict = <'key_one': 'val_one', 'key_two': 'val_two'>some_set = set(some_dict) print(some_set) > <'key_one', 'key_two'># элементы списка преобразуются в элементы множества, дубликаты удаляются card_suit = [‘heart’, ‘diamond’, ‘club’, ‘spade’, ‘spade’] suit_set = set(card_suit) print(suit_set) >
Однако в списках не должно быть вложенных изменяемых элементов.
tricky_list = [<'jocker': 'black'>, <'jocker': 'red'>] sad_set = set(tricky_list) print(sad_set) > Traceback (most recent call last): sad_set = set(tricky_list) TypeError: unhashable type: ‘dict’
Работа с set-ами
Создание
Чтобы получить аналогичный результат, необходимо передать итерируемый объект (список, строку или кортеж) в качестве аргумента:
# объявим список L L = [‘1’, ‘2’, ‘3’] # и предоставим его в set() S_2 = set(L) print(S_2) # так как set — коллекция неупорядоченная, то результат вывода может отличаться > <'1', '2', '3'>print(type(S_2)) >
👉 Замечание: пустое множество создаётся исключительно через set()
empty_set = set() print(empty_set) > set() print(type(empty_set)) >
Если же сделать так:
another_empty_set = <> print(another_empty_set) > <> print(type(another_empty_set)) >
То получим пустой словарь. А если внутри фигурных скобок поместить пустую строку:
maybe_empty_set = <''>print(maybe_empty_set) > <''>print(type(maybe_empty_set)) >
То на выходе увидим множество, состоящее из одного элемента — этой самой пустой строки.
# количество элементов множества print(len(maybe_empty_set)) > 1
Вполне естественно, что пустое множество, при приведении его к логическому типу, тождественно ложно:
true_or_false = set() print(bool(true_or_false)) > False
Пересечение
Добавление элемента
stats = <1.65, 2.33, 5.0>stats.add(14.7) print(stats) >
Если среди исходных объектов, составляющих set, «x» уже был, то ничего не произойдёт, и начальное множество не изменится.
big_cats = <'tiger', 'liger', 'lion', 'cheetah', 'leopard', 'cougar'>big_cats.add(‘cheetah’) # это жестоко, но второго гепарда не появится print(big_cats) >
Удаление и очистка
Очистить и свести уже существующий сет к пустому не составит никаких проблем благодаря методу сlear() :
set_with_elements = <'i am element', 'me too'>print(set_with_elements) > <'i am element', 'me too'>set_with_elements.clear() print(set_with_elements) > set()
Для удаления одного единственного компонента из набора в Питоне определены аж три способа.
triangle_coord = <(0, 4), (3, 0), (-3, 0)>print(triangle_coord) > <(3, 0), (-3, 0), (0, 4)>triangle_coord.discard((0, 4)) print(triangle_coord) > <(3, 0), (-3, 0)>triangle_coord.discard((54, 55)) print(triangle_coord) >
Удаляет и возвращает случайный элемент множества:
Перебор элементов
Множество, как и любую другую коллекцию, итерируем циклом for :
iterate_me = <1.1, 1.2, 1.3, 1.4, 1.5>for num in iterate_me: print(num) > 1.1 1.4 1.3 1.2 1.5
Принадлежность объекта set-у
Оператор in даёт возможность проверить наличие элемента в наборе:
berry_club = <'Tomato', 'Currant', 'Sea buckthorn', 'Grape', 'Barberry'>print(‘Tomato’ in berry_club) > True print(‘Strawberry’ in berry_club) > False
Сортировка множеств
Длина множества
Операции на множествах
Самое важное в этой теме. Математические теоретико-множественные операции, что не доступны никаким другим коллекциям языка. Поехали.
Объединение
Объединением двух множеств «X» и «Y» является такое третье множество «Z», каждый элемент которого принадлежит либо множеству «X», либо «Y».
lang_X = <'C++', 'Perl', 'PHP'>lang_Y = <'Java', 'C#', 'PHP', 'Python'>lang_Z = lang_X.union(lang_Y) # или так lang_Z = lang_X | lang_Y print(lang_Z) >
Пересечение
Пересечением двух множеств «A» и «B» является такое третье множество «C», каждый элемент которого принадлежит и множеству «A», и множеству «B».
bats_enemies = <'Darkside', 'Jocker', 'Bane'>sups_enemies = <'General Zod', 'Darkside', 'Lobo'>JL_enemies = bats_enemies.intersection(sups_enemies) # или так JL_enemies = bats_enemies & sups_enemies print(JL_enemies) >
Разность множеств
Разностью двух множеств «O» и «P» является такое третье множество «S», каждый элемент которого принадлежит множеству «O» и не принадлежит множеству «P».
Симметрическая разность
Симметрической разностью двух множеств «M» и «N» является такое третье множество «L», каждый элемент которого принадлежит либо множеству «M», либо «N», но не их пересечению.
f_set = <11, 'a', 18, 'v', 65, 'g'>s_set = <11, 'z', 32, 'v', 0, 'g'>t_set = f_set.symmetric_difference(s_set) # или так t_set = f_set ^ s_set print(t_set) >
Помимо теоретико-множественных операций, в питоне существуют и сугубо утилитарные производные методы.
isdisjoint()
Метод определяет, есть ли у двух set-ов общие элементы:
it = <'green', 'white', 'red'>ru = <'white', 'blue', 'red'>ukr = <'blue', 'yellow'># вернет False, если множества пересекаются print(ukr.isdisjoint(it)) > True # и True, в противном случае print(ru.isdisjoint(it)) > False
В Python нет оператора, который бы соответствовал этому методу.
issubset()
Показывает, является ли «I» подмножеством «J» (Метод вернет True, если все элементы «I» принадлежат «J»):
solar_system = <'Mercury', 'Venus', 'Earth', 'Mars', 'Jupiter', 'Saturn', 'Uranus', 'Neptune'>first_three_planets = <'Mercury', 'Venus', 'Earth'>poor_small_guy = <'Pluto'>emptyness = set() print(first_three_planets.issubset(solar_system)) # или так first_three_planets True print(poor_small_guy.issubset(solar_system)) # poor_small_guy False # как и в математике, пустое множество есть подмножество любого множества print(emptyness.issubset(solar_system)) # emptyness True # также любое множество является подмножеством самого себя print(poor_small_guy.issubset(poor_small_guy)) # poor_small_guy True
print(poor_small_guy.issubset(poor_small_guy)) # poor_small_guy False
issuperset()
Показывает, является ли «F» надмножеством «G»:
print(solar_system.issuperset(first_three_planets)) # solar_system >= first_three_planets > True print(poor_small_guy.issuperset(solar_system)) # poor_small_guy >= solar_system > False # в сердечке Плутона лишь пустота… print(poor_small_guy.issuperset(emptyness)) # poor_small_guy >= emptyness > True
print(poor_small_guy > poor_small_guy) > False
И для него в языке Python тоже не существует соответствующего метода.
update()
Изменяет исходное множество по объединению:
dogs_in_first_harness = <'Lessie', 'Bork', 'Spark'>dogs_in_second_harness = <'Lucky'>dogs_in_second_harness.update(dogs_in_first_harness) # или так dogs_in_second_harness |= dogs_in_first_harness print(dogs_in_second_harness) >
intersection_update()
difference_update()
symmetric_difference_update()
И, наконец, по симметрической разности:
his_bag = <'croissant', 'tea', 'cookies'>her_bag = <'tea', 'cookies', 'chocolate', 'waffles'>her_bag.symmetric_difference_update(his_bag) print(her_bag) # или так her_bag ^= his_bag >
Свойства методов и операторов
list_of_years = [2019, 2018, 2017] set_of_years = <2009, 2010, 2011>print(set_of_years.union(list_of_years)) > <2017, 2018, 2019, 2009, 2010, 2011>print(set_of_years | list_of_years) > Traceback (most recent call last):> print(set_of_years | list_of_years) TypeError: unsupported operand type(s) for |: ‘set’ and ‘list’
Но есть и сходства. Например, важным является то, что некоторые операторы и методы позволяют совершать операции над несколькими сетами сразу:
Тем интереснее, что оператор ^ симметрической разности позволяет использовать несколько наборов, а метод symmetric_difference() — нет.
tc1 = <10.1, 20.2, 30.3, 40.4, 50.5>tc2 = <10.1, 20.2, 30.3, 40.4, 500>tc3 = <1, 50.1, 1000>print(tc1 ^ tc2 ^ tc3) # вы же помните про порядок операций (слева-направо)? > <1, 1000, 50.1, 50.5, 500>print(tc1.symmetric_difference(tc2, tc3)) > Traceback (most recent call last): print(tc1.symmetric_difference(tc2, tc3)) TypeError: symmetric_difference() takes exactly one argument (2 given)
Преобразования
Конвертация строки во множество
Чтобы перевести строку во множество, достаточно представить её в виде литерала этого множества.
my_string = ‘Lorem ipsum dolor sit amet’ sting_to_set =
Конвертация списка во множество
Со списком подобный трюк не пройдет, но здесь на помощь спешит функция set() :
my_list = [2, 4, 8, 16, 32] list_to_set = set(my_list) print(list_to_set) >