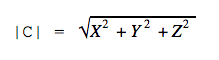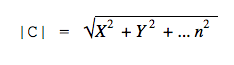Как умножить вектор на число

Особенности и правила умножения вектора на число

При обучении математике и физике в старших классах средней школы, а также в высших учебных заведениях постоянно приходится сталкиваться с понятием вектора. Учащиеся и студенты обязаны уметь проводить с векторами простейшие арифметические действия.

В статье будет показано, как умножать их на постоянные числа.

Основные понятия и определения

Чтобы в дальнейшем упростить работу со статьёй, введём некоторые формулировки и договорённости:

Это интересно: Как найти разность чисел в математике?

Правила умножения вектора на число

Рассмотрим, как умножить вектор на число:

Алгебраический и геометрический смысл действия

Любое математическое действие имеет некий смысл, причём в разных науках он различается. Рассмотрим, что нам даёт этот вид умножения:

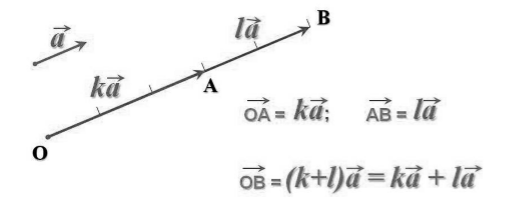
Формулы умножения

При умножении проще всего использовать заранее заученные на память формулы, которые вполне можно применять по шаблону, выполняя действия буквально на полном автомате:

Для начала возьмём физическую задачу воздействия силы на материальную точку. Пусть на неё действует сила, описываемая (АВ) (57;63;28). Как изменится эта сила по координатам при её десятикратном увеличении?

Прежде всего следует отметить, что направление воздействия силы не изменится, а сама сила возрастёт десятикратно. При раскладке по координатам получим следующее:

10*(АВ) (57;63;28) = (А1В1) (10*57;10*63;10*28) = (А1В1) (570;630;280).

Прежде всего заметим, что знак у постоянной отрицательный, следовательно, направление самой силы изменится на противоположное. Воспользуемся пунктом 2 вышеизложенных правил умножения, тогда сразу станет понятно, что численное выражение силы уменьшится вдвое. Проведём вычисления по шаблону:

-0,5*(АВ) (46;59;-43) = (А1В1) (-0,5*46;-0,5*59;-0,5*(-43)) = (А1В1) (-23;-29,5;21,5).

Следует заметить, что приведённые выше задачи решались для векторов, размещённых в пространстве и имеющих три координаты. В случае плоскостного размещения количество координат уменьшается до двух, а в случае линейного — до одной. Рассмотрим математические примеры для этих случаев:

Возможные действия с векторами

Не следует думать, что все возможные действия ограничиваются умножениям на число. Прежде всего можно определить длину (АВ) — модуль. Он будет равняться SQRT из суммы квадратов координат. Поясним это на примере:

Кроме этого, из курса школьной математики и физики известно, что вектора можно слагать один с другим и вычитать друг из друга. При этом проводится сложение и вычитание соответствующих координат.

Наконец, высшая математика вводит понятия числового (скалярного) и векторного умножения двух векторов. В первом случае получится некое число, во втором — третий вектор, направленный перпендикулярно плоскости, содержащей два первых.

В данной статье приведены основы умножения вектора на число. Исходя из её материала, можно утверждать, что действие это простое и доступное любому школьнику с удовлетворительной успеваемостью. Рекомендуется изучить формулы и в своих вычислениях действовать по изложенному в тексте шаблону. Что такое сравнение в литературе читайте в нашей статье.

Источник

Умножение вектора на число

Вы будете перенаправлены на Автор24

Откладывание вектора от данной точки

Для того чтобы ввести понятие умножения вектора на число, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.

Введем следующую теорему:

Доказательство.

Существование: Здесь нужно рассмотреть два случая:

Рисунок 2. Иллюстрация теоремы 1

Единственность: единственность сразу следует из построения, проведенного в пункте «существование».

Теорема доказана.

Умножение вектора на число

Отметим, что в результате произведения вектора на число всегда получается векторная величина.

Свойства произведения вектора на число

Произведение любого вектора с числом ноль равняется нулевому вектору.

Доказательство.

Доказательство.

Доказательство этого закона иллюстрирует рисунок 3.

Рисунок 3. Сочетательный закон

Доказательство этого закона иллюстрирует рисунок 4.

Рисунок 4. Первый распределительный закон

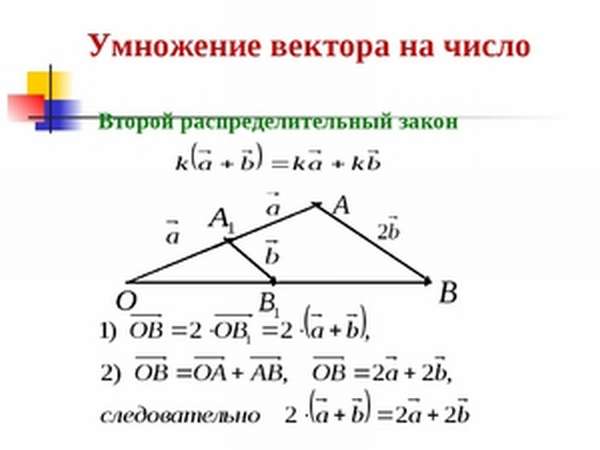
Доказательство этого закона иллюстрирует рисунок 5.

Рисунок 5. Второй распределительный закон

Готовые работы на аналогичную тему

Пример задачи на использование понятия произведения вектора на число

Источник

Операции с векторами

Как сложить и перемножить векторы (и зачем).

Мы постепенно показываем вам математику за пределами школьной программы. Начинали со знакомства с векторами, теперь сделаем следующий шаг.

Напомним основные мысли:

С векторами можно совершать некоторые математические операции. Вот о них и поговорим.

Правильно — векторы

Математики часто говорят во множественном числе «вектора», но по словарю правильно «векторы». Это такой профессиональный жаргон, как «договора», «бухгалтера» и «сервера». Мы будем использовать «векторы», но если вы окажетесь в постковидном математическом баре, лучше говорите «вектора».

Сложение

Представим четыре вектора, которые лежат в двухмерном пространстве и пока что не связаны между собой. Нарисуем эти векторы и обозначим их буквами X, Y, Z, K.

Поскольку векторы находятся в одном пространстве, координаты каждого состоят из одинакового количества чисел. У нас пример с двухмерным пространством и два числа. Выглядеть это будет так: X = (6, 4); Y = (3, −2); Z = (−7, −5); K = (−10, 4).

Векторы X, Y, Z, K в двухмерном пространстве

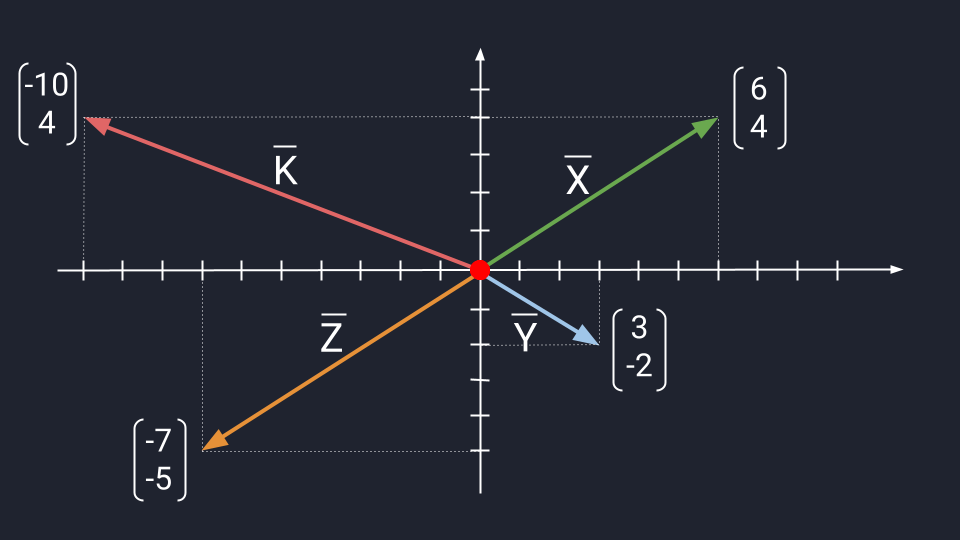
Если у нас несколько векторов с одинаковым количеством чисел, то эти числа можно поэлементно складывать. Для этого мы берём первое число одного вектора, складываем его с первым числом другого вектора и так далее.

Предположим, нам нужно сложить векторы X и Y.

X = (6, 4)
Y = (3, −2)
X + Y = (9, 2)

Вроде просто: складываешь последовательно все координаты, результаты сложения складываешь в исходные коробочки. Так можно делать с любым количеством координат. Помните, что вектор — это необязательно стрелка в двумерном пространстве. Она может быть и в десятимерном пространстве — с точки зрения математики это неважно.

Например, вот сложение векторов с пятью координатами:

Интуитивное изображение сложения

Для интуитивного восприятия удобно использовать векторы с двумя координатами. Их удобно рисовать на координатной плоскости и таким образом смотреть на геометрию.

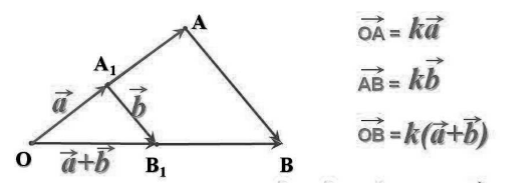
Например, можно на плоскости показать, как будет работать сложение двух векторов. Для этого есть два метода: метод треугольника и метод параллелограмма.

Метод треугольника: ставим векторы Х и Y в очередь друг за другом. Для этого берём вектор Х, ставим за ним вектор Y и получаем новый вектор. Новый вектор начинается в хвосте вектора Х и заканчивается на стрелке вектора Y. Этот вектор — результат сложения. Представьте, что это ребёночек двух векторов.

Сложение векторов по методу треугольника: X = (6, 4); Y = (3, −2); Х + Y = (9, 2)

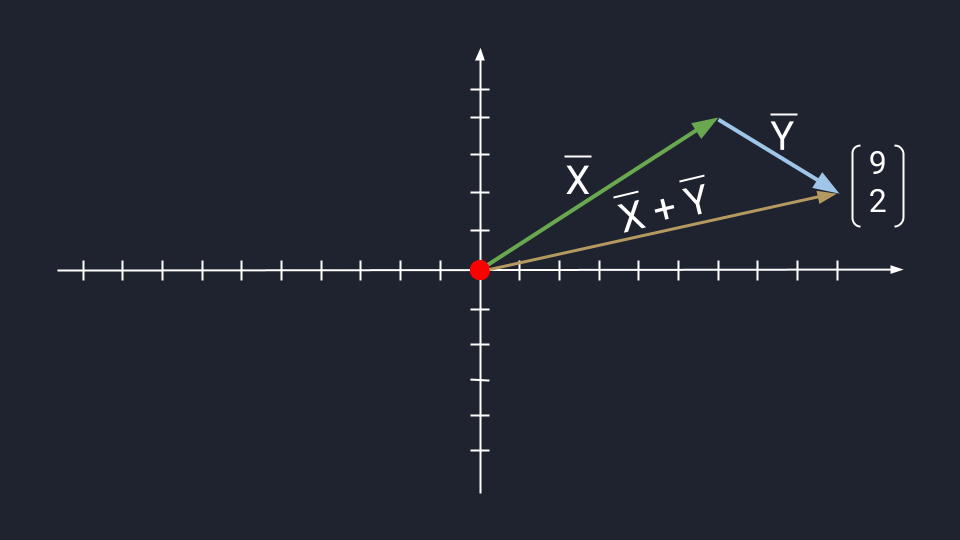
Чтобы воспользоваться методом параллелограмма, нам нужно поставить векторы Х и Y в одну исходную точку. Дальше мы дублируем векторы Х и Y, формируем параллелограмм и получаем новый вектор. В новом векторе соединяем исходную точку с исходной точкой дублирующих векторов — стрелка проходит посередине параллелограмма. Длина нового вектора — это сумма векторов Х и Y.

Сложение по методу параллелограмма и треугольника даёт одинаковый результат. Поэтому выбирайте вариант, который больше подходит под задачу.

Вычитание

Вычитание векторов немного сложнее. Чтобы вычесть векторы, нужно «развернуть» вычитаемый вектор и сложить его с исходным. «Развернуть» — то есть направить в обратную сторону, «перевернув» знаки координат. Получится конструкция вроде такой: Х + (−Y)

Дальше используются правила сложения. Пошагово это выглядит так:

Теперь посмотрим, как выглядит вычитание векторов на графике:

Вычитание векторов по методу треугольника: X = (6, 4); −Y = (−3, 2); X + (−Y) = (3, 6) Вычитание векторов по методу параллелограмма: X = (6, 4); −Y = (−3, 2); X + (−Y) = (3, 6)

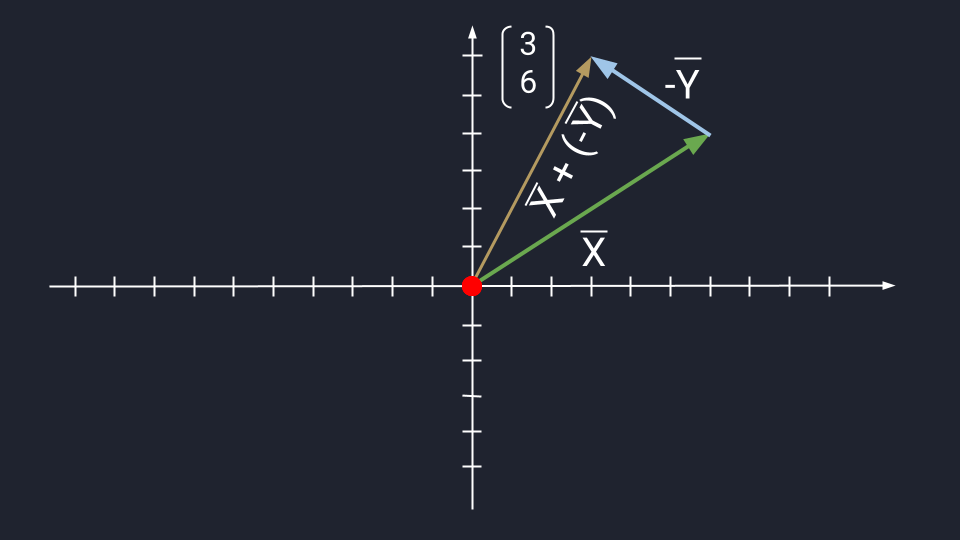
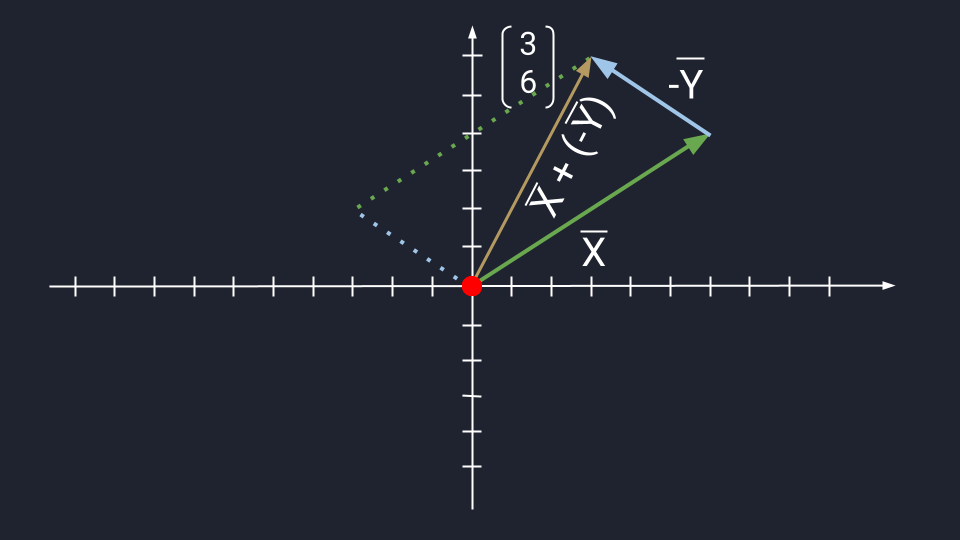
Длина вектора

Длина вектора — это одно число, которое измеряется расстоянием от кончика до стрелки вектора. Длину вектора нельзя путать с координатами. Координаты — это несколько чисел, которые указывают на расположение стрелки вектора. По координатам можно определить только конечную точку вектора. Например, если X = (6, 2), то стрелка будет находиться в точке 6 по оси Х. Или другой пример: если Y = (6, 5), то стрелка этого вектора будет находиться в точке 5 по оси Y.

Предположим, нам известны начальные точки векторов X и Y. Пусть это будет точка 2 по оси X и точка 2 по оси Y. Так мы можем легко посчитать длину отрезков:

X = 6 − 2 = 4
Y = 5 − 2 = 3

Иногда приходится рассчитывать длину третьего вектора, который привязан к двум другим векторам. Это легко сделать с помощью теоремы Пифагора — это когда квадрат гипотенузы равен сумме квадратов катетов. В нашем случае катетами будут длины векторов X и Y. Вспоминаем школьную формулу и считаем:

|C|2 = 42 + 32 = 25
|C| = √25 = 5 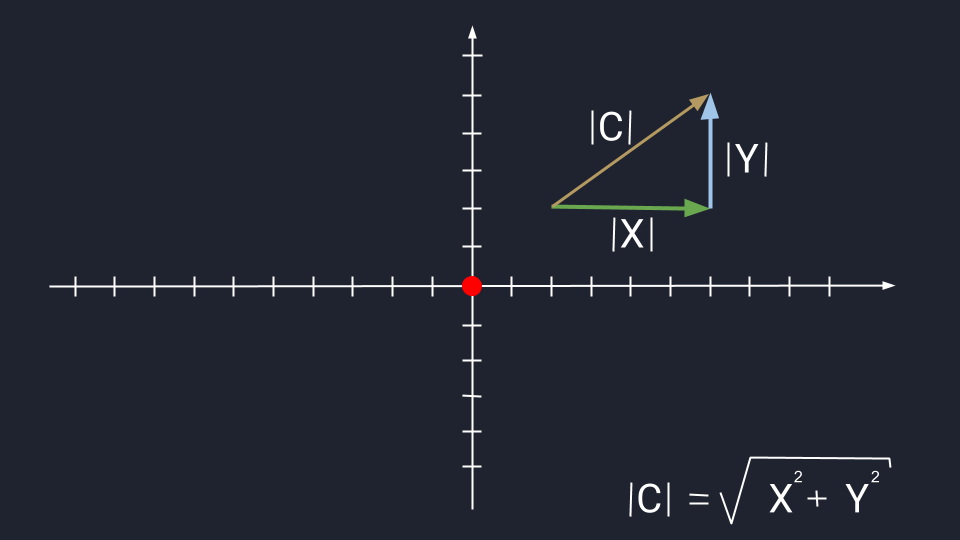Длина вектора считается по формуле прямоугольного треугольника. Чтобы было проще представить — перенесите векторы на систему координат

Это формула для двумерного пространства. В трёхмерном пространстве формула похожая: нужно сложить квадраты трёх координат и вычислить квадратный корень из суммы.

В пространстве с большим числом измерений формула выглядит сложнее, но по сути то же: складываем все квадраты координат и получаем квадратный корень из этой суммы.

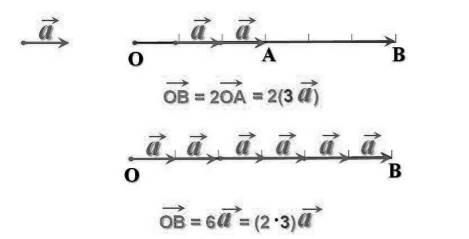
Умножение и деление вектора на число

Умножение и деление позволяют изменить длину и направление вектора. Если мы умножим вектор Х на три, то увеличим его длину в три раза. Если умножим на минус три — увеличим длину и изменим его направление на противоположное.

Умножение вектора на число

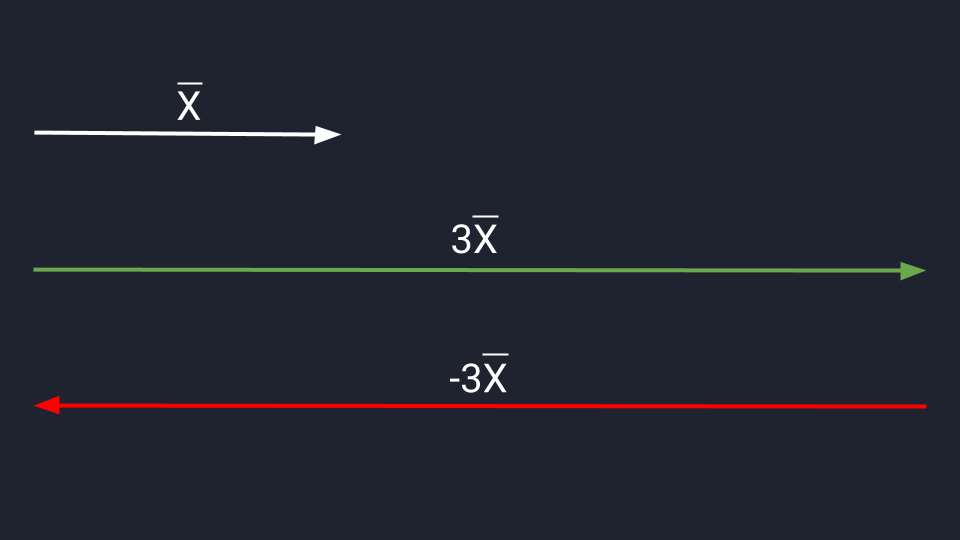
Для деления сохраняются аналогичные правила. Делим вектор Х на три и сокращаем длину в три раза. Делим на минус три — сокращаем и разворачиваем.

Деление вектора на число

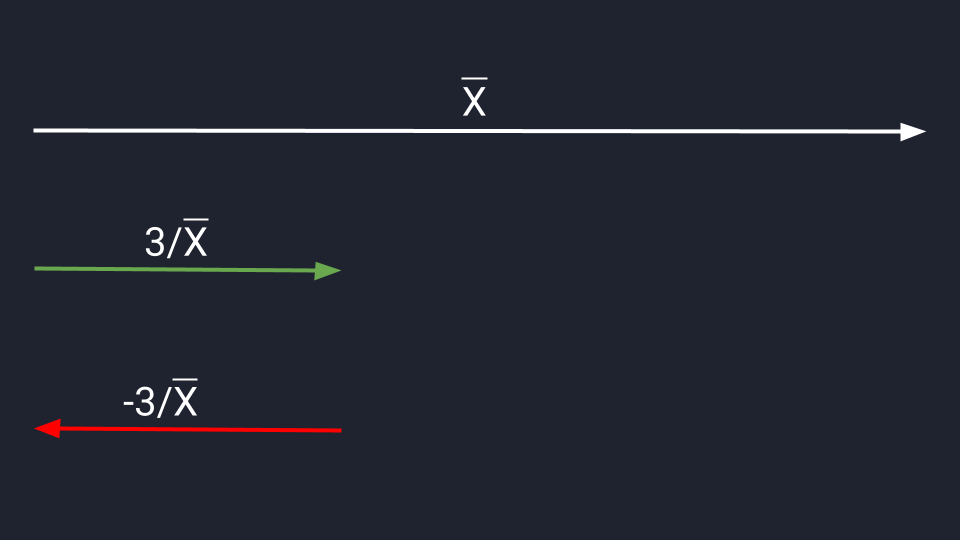
Да вроде несложно!

Пока ничего сложного. Но если углубляться, вы узнаете, что:

Что дальше

В следующей статье рассмотрим линейную зависимость векторов. Чтобы не скучать — посмотрите интервью с Анастасией Никулиной. Анастасия сеньор-дата-сайентист в Росбанке и по совместительству блогер с интересной историей.

Источник

Особенности и правила умножения вектора на число

При обучении математике и физике в старших классах средней школы, а также в высших учебных заведениях постоянно приходится сталкиваться с понятием вектора. Учащиеся и студенты обязаны уметь проводить с векторами простейшие арифметические действия.

В статье будет показано, как умножать их на постоянные числа.

Основные понятия и определения

Чтобы в дальнейшем упростить работу со статьёй, введём некоторые формулировки и договорённости:

Это интересно: Как найти разность чисел в математике?

Правила умножения вектора на число

Рассмотрим, как умножить вектор на число:

Интересно знать: Модуль числа в математике.

Алгебраический и геометрический смысл действия

Любое математическое действие имеет некий смысл, причём в разных науках он различается. Рассмотрим, что нам даёт этот вид умножения:

Это интересно: как разложить на множители квадратный трехчлен?

Формулы умножения

При умножении проще всего использовать заранее заученные на память формулы, которые вполне можно применять по шаблону, выполняя действия буквально на полном автомате:

Для начала возьмём физическую задачу воздействия силы на материальную точку. Пусть на неё действует сила, описываемая (АВ) (57,63,28). Как изменится эта сила по координатам при её десятикратном увеличении?

Прежде всего следует отметить, что направление воздействия силы не изменится, а сама сила возрастёт десятикратно. При раскладке по координатам получим следующее:

10*(АВ) (57,63,28) = (А1В1) (10*57,10*63,10*28) = (А1В1) (570,630,280).

Прежде всего заметим, что знак у постоянной отрицательный, следовательно, направление самой силы изменится на противоположное. Воспользуемся пунктом 2 вышеизложенных правил умножения, тогда сразу станет понятно, что численное выражение силы уменьшится вдвое. Проведём вычисления по шаблону:

-0,5*(АВ) (46,59,-43) = (А1В1) (-0,5*46,-0,5*59,-0,5*(-43)) = (А1В1) (-23,-29,5,21,5).

Следует заметить, что приведённые выше задачи решались для векторов, размещённых в пространстве и имеющих три координаты. В случае плоскостного размещения количество координат уменьшается до двух, а в случае линейного — до одной. Рассмотрим математические примеры для этих случаев:

Возможные действия с векторами

Не следует думать, что все возможные действия ограничиваются умножениям на число. Прежде всего можно определить длину (АВ) — модуль. Он будет равняться SQRT из суммы квадратов координат. Поясним это на примере:

Кроме этого, из курса школьной математики и физики известно, что вектора можно слагать один с другим и вычитать друг из друга. При этом проводится сложение и вычитание соответствующих координат.

Наконец, высшая математика вводит понятия числового (скалярного) и векторного умножения двух векторов. В первом случае получится некое число, во втором — третий вектор, направленный перпендикулярно плоскости, содержащей два первых.

В данной статье приведены основы умножения вектора на число. Исходя из её материала, можно утверждать, что действие это простое и доступное любому школьнику с удовлетворительной успеваемостью. Рекомендуется изучить формулы и в своих вычислениях действовать по изложенному в тексте шаблону.

Источник

Умножение вектора на число

Пусть в E n введена декартова система координат.

Определение. Умножить вектор на действительное число l Î R означает найти вектор Î V n такой, что его координаты = l .

Обозначение: = l

Замечания.

1) Ясно, что определение умножения вектора на число сформулировано для фиксированной системы координат, и требуется доказательство корректности определения (то есть того, что результат умножения вектора на число не зависит от выбора системы координат).

2) В определении не утверждается существование вектора , этот факт требует отдельного доказательства.

3) Интересен вопрос о геометрическом смысле умножения вектора на число; как это умножение выглядит для представителей векторов – для направленных отрезков.

4) При умножении вектора на число ноль получится нуль-вектор не зависимо от системы координат, и при умножении нуль-вектора на любое число получится нуль-вектор не зависимо от системы координат.

Лемма. Любой вектор можно умножить на любое число, причем в данной системе координат результат определен однозначно.

Доказательство.

Найдем вектор = l .

Возьмем направленный отрезок , где точка O – начало координат, точка B (l ).

Координаты этого направленного отрезка равны = (l ).

Пусть вектор такой, что = .

Тогда по определению = l .

Единственность (в данной системе координат).

Пусть вектор такой, что = l , тогда его координаты по определению _’ = l , то есть _’ = и = .

Лемма (Простейшие свойства умножения вектора на число (в данной системе координат)).

1) Если = l , то | | = | l | | | для любых векторов , Î V n и любого числа l Î R.

3) lq = q для любого числа l Î R.

5) (l m) = l (m ) = m (l ) для любого вектора Î V n и любых чисел l, m Î R

Доказательство.

1. Пусть = l , и пусть координаты этих векторов =( ), = ( ). Тогда по определению = l .

Найдем длины этих векторов: | | = || ||, | | = || l || = | l | || || = | l | | |.

2. Пусть координаты вектора = ( ). Тогда координаты вектора 0 будут следующие: (0´ ) = q.

3. Так как все координаты нуль-вектора равны нулю, при умножении их на число l эти координаты останутся нулевыми, а значит, зададут нулевой вектор.

4. Координаты векторов и 1 ´ совпадают, так как координаты вектора при умножении число 1 не изменятся, следовательно, = 1 ´ .

5. Пусть координаты вектора = ( ). Найдем координаты векторов (l m) , l (m ) и m (l ): (l m) = (lm) , l (m ) = l( m )= (lm) , m (l ) = m (l ) = (l m) . Координаты данных векторов равны, следовательно и векторы равны друг другу.

Лемма.Пусть векторы , Î V n ( ≠ q) отложены от одной точки O так, что = , = . Тогда для того чтобы = l (l Î R) необходимо и достаточно, чтобы точка B делила OA в отношении l.

Доказательство.

1) Пусть = l и = , = .

Выразим координаты векторов и через координаты точек O,A и B:

координаты вектора : = —

координаты вектора : = —

Так как = l , то — = l ( — ), то есть = (1-l) + l .

Следовательно, точка B делит OA в отношении l.

2) Пусть точки O,A и B такие, что точка B делит OA в отношении l и = , = .

Так как B делит OA в отношении l, то = (1-l) + l , то есть

— = l ( — ), и координаты векторов и таковы, что = l .

Следовательно, = l .

Доказательство.

1) Пусть существует число l Î R, l ≠ 0 такое, что = l (l ≠ 0).

Отложим вектор от точки O’: = .

Тогда OO’A’A – параллелограмм (см. § 8), следовательно, O’A’ | | OA.

С другой стороны, точки O’,A’ и B лежат на одной прямой, поэтому OA | | O’B.

2) Пусть векторы = , = ( ≠ q, ≠ q) и OA | | O’B. Отложим вектор от точки O’: = . Тогда четырехугольник OO’A’A является параллелограммом и O’A’ | | OA, значит точки O’,A’ и B лежат на одной прямой.

Та как точки O’ и A’ различны ( ≠ q ), то существует такое число l Î R, что точка B делит O’A’ в отношении l. Следовательно, = l .

Определение. Будем называть векторы и коллинеарными, если существует такое число l Î R, что = l или = l .

Обозначение: | | .

Замечания.

1) Нуль-вектор коллинеарен любому вектору.

2) Как видно из геометрического «смысла» умножения вектора на число два вектора коллинеарны тогда и только тогда, когда их представители лежат на одной прямой или на параллельных прямых.

3) Как видно из определения коллинеарности векторов, векторы коллинеарны тогда, и только тогда, когда их координаты пропорциональны.

Обозначение: ­­ .

Замечание.

1) Два не нулевых вектора и сонаправлены тогда и только тогда, когда при = , = лучи OA и OB совпадают.

2) Два не нулевых вектора и сонаправлены тогда и только тогда, когда при = , = точки A и B лежат по одну сторону от прямой OO’.

Обозначение: ­¯ .

Определение. Два направленных отрезка будем называть коллинеарными (сонаправленными, противоположно направленными), если они являются представителями коллинеарных (сонаправленных, противоположно направленных) векторов.

Упражнения.

1. Является коллинеарность (сонаправленность) на множестве V n отношением эквивалентности?

2. Докажите, что два направленных отрезка равны тогда, и только тогда, когда они сонаправлены и имеют одинаковые длины.

Сумма векторов

Пусть в E n фиксирована декартова система координат.

Обозначение: = + — « вектор равен сумме векторов и .

Замечание. Определение суммы введено при фиксированной системе координат, и пока не ясно зависит ли результат суммы двух векторов от выбора системы координат.

Теорема. (Свойства суммы векторов).

4. Для любого вектора Î V n существует вектор (- )ÎV n такой, что + (- ) = q

5. l ( + ) = l + l для любых векторов , Î V n и любого числа l Î R.

6. (l + m) = l + m для любого вектора Î V n и любых чисел l, m Î R.

Доказательство.

1) Так как + = + , то + = + .

2) Так как + ( + ) = ( + ) + , то + ( + ) = ( + ) + .

3) Так как + = , то + q = .

4) Пусть = ( ), возьмем вектор (- ) с координатами: (- ) = (- ).

Так как + (- ) = , то + (- ) = q.

5) Так как l( + ) = l + l , то l( + ) = l + l .

6) Так как (l + m) = l + m , то (l + m) = l + m .

Замечание.

Свойства 1- 4 операции суммы векторов говорят о том, что множество V n относительно операции суммы – это коммутативная группа.

Определение. Вектор (- ) такой, что + (- ) = q будем называть противоположным к вектору .

Замечания.

1) Для нуль-вектора противоположным будет тоже нуль-вектор.

2) Вектор противоположный к противоположному к вектору — это вектор ,

4) Для любого вектора существует единственный вектор противоположный к данному.

Теорема. (Правило треугольника для суммы векторов).

Пусть , Î V n и точки A,B,C Î E n такие, что = , = . Тогда = + .

Доказательство.

Пусть = ( ), = ( ), A ( ), B ( ) и C ( ), и пусть вектор такой, что

= + .

Так как = , = , то — = и — = .

Тогда координаты вектора будут следующими:

+ = ( — ) + ( — ) = — , то есть = .

Следствие. Результат суммы векторов не зависит от выбора системы координат.

Доказательство.

Следствие. Пусть = , тогда = (- ).

Доказательство.

Так как + = = q, то — представитель вектора противоположного вектору .

Следствие. (Правило параллелограмма для суммы двух векторов.)

Пусть , Î V n – не коллинеарные векторы, точки A,B,C, D Î E n такие, что = , = и ABCD – параллелограмм. Тогда = + .

Доказательство.

Так как ABCD – параллелограмм, то = = (см. § 8), поэтому + = + = .

Определение. Разностью вектора и вектора будем называть вектор, который равен сумме вектора и вектора (- ).

Обозначение: — = + (- ).

Следствие. = — Û = — .

Замечание. Множество векторов V n с операциями умножения на число и суммой элементов является частным случаем векторного (линейного) пространства. В дальнейшем будем употреблять термин «пространство V n » подразумевая множество V n вместе с данными операциями.

Упражнения.

2) Докажите правило параллелограмма для суммы векторов, не ссылаясь на правило треугольника.

4) Докажите, что для любого вектора Î V n существует единственный вектор ÎV n такой, что + = q.

5) Сформулируйте и докажите правило аналогичное правилу треугольника для разности векторов.

Источник