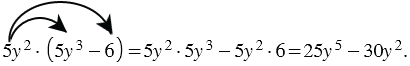Как умножить одночлен многочлен

Умножение многочлена на одночлен: правило, примеры

Частный случай умножения многочлена на многочлен – умножение многочлена на одночлен. В этой статье сформулируем правило совершения этого действия и разберем теорию на практических примерах.

Правило умножения многочлена на одночлен

Приведенные рассуждения позволяют нам сформулировать правило умножения многочлена на одночлен:

Для осуществления действия умножения многочлена на одночлен необходимо:

Дополнительно поясним приведенный алгоритм.

Рассмотренные примеры дают возможность заметить важный нюанс: в результате перемножения многочлена и одночлена получается многочлен. Данное утверждение верно для любых перемножаемых многочлена и одночлена.

По аналогии осуществляется умножение одночлена на многочлен: заданный одночлен перемножают с каждым членом многочлена и полученные произведения суммируются.

Примеры умножения многочлена на одночлен

Решение

Первый шаг правила уже выполнен – произведение записано. Теперь выполняем следующий шаг, умножая каждый член многочлена на заданный одночлен. В данном случае удобно сначала перевести десятичные дробив обыкновенные. Тогда получим:

Уточним, что, когда исходные многочлен и/или одночлен заданы в нестандартном виде, перед тем, как найти их произведение, желательно привести их к стандартному виду.

Решение

Мы видим, что исходные данные представлены в нестандартном виде, поэтому для удобства дальнейших вычислений приведем их в стандартный вид:

Теперь осуществим перемножение одночлена a 2 · b на каждый член многочлена 1 + 4 · a − 2 · a 2

a 2 · b · ( 1 + 4 · a − 2 · a 2 ) = a 2 · b · 1 + a 2 · b · 4 · a + a 2 · b · ( − 2 · a 2 ) = = a 2 · b + 4 · a 3 · b − 2 · a 4 · b

Мы могли бы не приводить исходные данные к стандартному виду: решение при этом оказалось бы более громоздким. При этом последним шагом возникал бы необходимость приведения подобных членов. Для понимания приведем решение по этой схеме:

Источник

Умножение одночленов: правило и решение примеров

Как мы уже выяснили, одночлены можно перемножать между собой. В этой статье мы объясним, как правильно выполнить умножение одного одночлена на другой. Сначала сформулируем основное правило, а потом разберем несколько типовых задач.

Основное правило умножения одночленов

Мы видим, что результатом умножения стал новый одночлен. Запишем его в стандартной форме:

7 · a · b · 2 · a · 7 · a 2 = ( 7 · 2 · 7 ) · ( a · a · a 2 ) · b = 98 · a 4 · b

Таким образом, мы умножили одночлен на другой и получили в итоге новый одночлен. Используя данный пример, можно сформулировать основное правило такого умножения.

Чтобы умножить один одночлен на другой, нужно выполнить следующие действия:

Теперь покажем, как применить этот алгоритм на практике.

Решение задач на умножение многочленов

Учитывая написанное выше, можно сказать, что для быстрого умножения многочленов нужно уметь раскрывать скобки в произведениях, группировать множители, перемножать между собой числа и степени с одинаковыми основаниями. Разберем такие задачи.

Решение

Выполним все действия по алгоритму, приведенному выше. Для нахождения произведения исходных одночленов сначала правильно запишем его:

3 8 · x 2 · y · 4 15 · x · y

Раскроем скобки и получим в результате следующий многочлен:

3 8 · x 2 · y · 4 15 · x · y

Нам осталось привести его к стандартному виду. Для этого выполним группировку чисел и множителей с одинаковыми переменными и получим:

3 8 · x 2 · y · 4 15 · x · y = 3 8 · 4 15 · x 2 · x · ( y · y )

Теперь нам нужно умножить обыкновенные дроби и применить основное свойство степени:

3 8 · 4 15 · x 2 · x · ( y · y ) = 1 10 · x 2 + 1 · y 1 + 1 = 1 10 · x 3 · y 2

Вот запись всего решения без комментариев:

3 8 · x 2 · y · 4 15 · x · y = 3 8 · x 2 · y · 4 15 · x · y = 3 8 · 4 15 · x 2 · x · ( y · y ) = = 1 10 · x 2 + 1 · y 1 + 1 = 1 10 · x 3 · y 2

Если у нас в условии стоит не два одночлена, а три, четыре и более, то мы действуем точно таким же образом.

Решение

Начнем с записи нужного произведения.

Теперь выполним раскрытие скобок и получим:

Нам осталось только привести этот одночлен к стандартному виду:

Также отметим, что при возведении одночлена в степень нам нужно будет выполнить все те же действия, поскольку возведение в степень представляет из себя умножение определенного количества одинаковых множителей.

Источник

Умножение многочлена на многочлен

Определение многочлена

Прежде чем мы расскажем, как умножить один многочлен на другой многочлен, разберемся в основных понятиях.

Одночлен — это произведение чисел, переменных и степеней.

Многочлен— алгебраическое выражение, которое представляет из себя сумму или разность нескольких одночленов.

Стандартный вид многочлена — представление многочлена в виде суммы одночленов стандартного вида, среди которых нет подобных одночленов.

Как привести многочлен к стандартному виду:

Вспомним, как умножать многочлен на одночлен, двучлен на двучлен, трехчлен на трехчлен:

(a + b) * (c + d) = ac + ad + bc + bd.

(a + b + c) * (x + y) = ax + bx + cx + ay + by + cy.

(a + b + c) 2 = a 2 + b 2 + c 2 + 2ab + 2ac + 2bc.

Эти правила можно описать так: чтобы умножить один многочлен на другой, нужно каждый член первого умножить на каждый член второго многочлена. Затем полученные произведения сложить и привести результат к многочлену стандартного вида, если это возможно.

Правило умножения многочлена на многочлен

Рассмотрим пример, а после решения сформулируем правило умножения многочлена на многочлен:

Правило умножения многочлена на многочлен

Чтобы умножить многочлен на многочлен, надо каждый член первого многочлена умножить на каждый член второго многочлена и все полученные произведения сложить.

Алгоритм умножения многочлена на многочлен:

Рассмотрим пример умножения многочлена на многочлен:
(6x – 2a) * (4 – 3x).

Ответ: (6x – 2a) * (4 – 3x) = 24x – 18x 2 – 8a + 6ax.

Рассмотрим пример умножения трех многочленов:
(x – 2) * (3x + 1) * (4x – 3).

Ответ: (x – 2) * (3x + 1) * (4x – 3) = 12x 3 – 29x 2 + 7x + 6.

Теперь мы знаем все из темы умножения многочлена на многочлен. Осталось отточить на практике новый навык и ловить хорошие и отличные отметки на контрольных.

Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Примеры умножения многочлена на многочлен

Рассмотрим еще несколько примеров, чтобы закрепить пройденный материал.

Пример 1. Выполнить умножение многочленов:
2 − 3x и x 2 − 7x + 1.

Запишем произведение: (2 − 3x)(x 2 − 7x + 1).

Из полученных выражений составим сумму: 2x 2 + 2(−7x) + 2*1 − 3xx 2 − 3x(−7x) − 3x*1.

Чтобы убедиться, что мы все сделали правильно, посчитаем количество членов в полученной сумме. Их шесть. Так и должно быть, так как исходные многочлены состоят из 2 и 3 членов: 2 * 3 = 6.

Осталось полученную сумму преобразовать в многочлен стандартного вида:

Пример 2. Найти произведение трех многочленов:
x 2 + xy − 1, x + y и 2y − 3.

Запишем их произведение: (x 2 + xy − 1)(x + y)(2y − 3).

Умножим первые два многочлена:

(x 2 + xy − 1)(x + y) = x 2 x + x 2 y + xyx + xyy − 1x − 1y = x 3 + 2x 2 y + xy 2 − x − y.

Таким образом: (x 2 + xy − 1)(x + y)(2y − 3) = (x 3 + 2x 2 y + xy 2 − x − y)(2y − 3).

Снова выполним умножение двух многочленов:

(x 3 + 2x 2 y + xy 2 − x − y)(2y − 3) = x 3 2y + x 3 (−3) + 2x 2 y 2 y + 2x 2 y(−3) + xy 2 2y + xy 2 (−3) − x 2 y − x(−3) − y 2 y − y(−3) = 2x 3 y − 3x 3 + 4x 2 y 2 − 6x 2 y + 2xy 3 − 3xy 2 − 2xy + 3x − 2y 2 + 3y.

Ответ: (x 2 + xy − 1)(x + y)(2y − 3) = 2x 3 y − 3x 3 + 4x 2 y 2 − 6x 2 y + 2xy 3 − 3xy 2 − 2xy + 3x − 2y 2 + 3y.

Источник

Действия с одночленами и многочленами

Как сложить одночлены

Два подобных одночлена можно сложить, и их сумма — это одночлен подобный слагаемым, с числовым коэффициент равным сумме числовых коэффициентов слагаемых. Так сложить можно только подобные одночлены. Сумма неподобных одночленов — это не одночлен, а многочлен.
3 × a 5 × b 4 + 7,3 × a 5 × b 4 =
= 10,3 × a 5 × b 4

Как умножить одночлен на одночлен

Чтобы умножить одночлен на одночлен, надо перемножить коэффициенты, показатели степеней одинаковых переменных сложить. Перемножить можно любые два одночлена — и подобные и неподобные.

7 × a 3 × b 4 × 2 × a × b 5 =
14 × a 4 × b 9

Как разделить одночлен на одночлен

Чтобы разделить одночлен на одночлен, надо разделить коэффициенты, показатели степеней одинаковых переменных вычесть.

(21 × a 4 × b 5 ) : (3 × a 2 ) =
7 × a 2 × b 5

Как умножить одночлен на многочлен

Чтобы умножить одночлен на многочлен, надо одночлен умножить на каждый член многочлена.

3 × a × b × [ 7 × a 3 × b 4 + 2 × a × b 5 × y ] =
21 × a 4 × b 5 + 6 × a 2 × b 6 × y

Как разделить многочлен на одночлен

Чтобы разделить многочлен на одночлен, надо каждый член многочлена разделить на этот одночлен.

Как умножить многочлен на многочлен

Чтобы умножить многочлен на многочлен надо умножить каждый член первого многочлена на каждый член второго многочлена.

Деление многочлена на многочлен Пример 1

Сейчас я покажу, как делить многочлен на многочлен в столбик. Обращаю ваше внимание на то, что не всякие два многочлена делятся один на другой. В этом видео специально подобраны пары многочленов, которые делятся один на другой. Также обращаю внимание на то, что для удобства деления слагаемые в многочленах нужно располагать в порядке убывания степеней — здесь в примерах слагаемые будут уже расставлены в нужном порядке. Чтобы поделить многочлены, нужно циклично повторять четыре действия: подели, занеси, умножь, вычти.

Пример 1: (12 × a 5 + 13 × a 4 + 3 × a 3 + 12 × a 2 + 9 × a) : (4 × a 2 + 3 × a)

Слагаемые расставлены в порядке убывания степени a.

Поделим старшее слагаемое остатка на старшее слагаемое делителя: (12 × a 2 ) : (4 × a 2 ) — получается 3. Заносим 3 в ответ ( + 3). Умножим весь делитель на 3 — получается 12 × a 2 + 9 × a. Запишем это произведение под остатком — каждое слагаемое произведения под соответствующей степенью остатка. Вычтем произведение из остатка — остаётся ноль.

Значит, многочлены поделились без остатка, и частное равно 3 × a 3 + a 2 + 3.

Деление многочлена на многочлен Пример 2

(-28 × a 5 + 24 × a 4 — 35 × a 3 — 6 × a 2 — 45) : (4 × a 2 + 5)

Слагаемые расставлены в порядке убывания степени a.

Деление многочлена на многочлен Пример 3

Пример 3: (54 × a 6 — 63 × a 5 + 42 × a 4 + 185 × a 3 — 136 × a 2 + 8 × a + 72) : (-9 × a 3 + 8 × a — 8)

Слагаемые расставлены в порядке убывания степени a.

Поделим старшее слагаемое остатка на старшее слагаемое делителя: (90 × a 4 ) : (-9 × a 3 ) — получается (-10 × a). Заносим (-10 × a) в ответ ( — 10 × a). Умножим весь делитель на ( — 10 × a) — получается 90 × a 4 — 80 × a 2 + 80a. Запишем это произведение под остатком — каждое слагаемое произведения под соответствующей степенью остатка. Вычтем произведение из остатка — остаётся 81 × a 3 — 72 × a + 72.

Источник

Умножение одночлена на многочлен

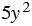
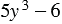
Умножим одночлен на многочлен .

Для этого составим их произведение и, используя распределительное свойство умножения, преобразуем его. Для этого умножим одночлен на каждый член многочлена и сложим результаты:

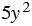
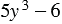
То есть произведение одночлена и многочлена мы представили в виде многочлена .

Вообще, произведение одночлена и многочлена всегда можно представить в виде многочлена. При умножении одночлена на многочлен пользуются правилом:

Приведённое правило позволяет умножать многочлен на одночлен, так как для произведения одночлена и многочлена справедливо переместительное свойство умножения относительно сложения и вычитания.

Поделись с друзьями в социальных сетях:

Источник