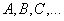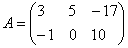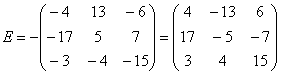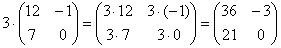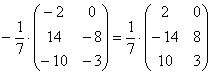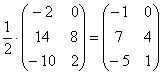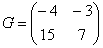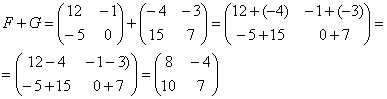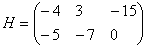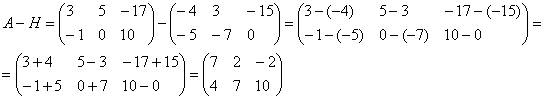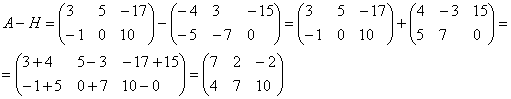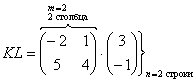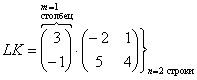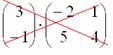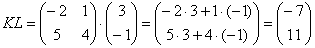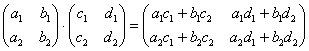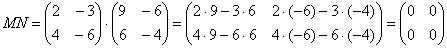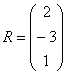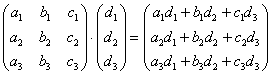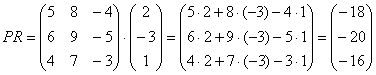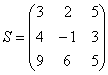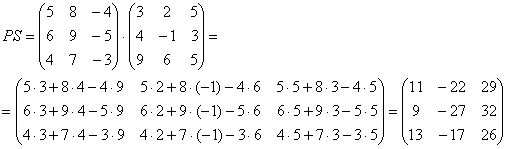Как умножить несогласованные матрицы
Умножение матриц
Итак, в предыдущем уроке мы разобрали правила сложения и вычитания матриц. Это настолько простые операции, что большинство студентов понимают их буквально с ходу.
Однако вы рано радуетесь. Халява закончилась — переходим к умножению. Сразу предупрежу: умножить две матрицы — это вовсе не перемножить числа, стоящие в клеточках с одинаковыми координатами, как бы вы могли подумать. Тут всё намного веселее. И начать придётся с предварительных определений.
Согласованные матрицы
Ещё раз: количество столбцов в первой матрице равно количеству строк во второй! Отсюда получаем сразу два вывода:
Определение умножения
По-моему, тут всё очевидно. Дальше можно не читать. [на самом деле нет]
У тех, кто впервые видит это определение, сразу возникает два вопроса:
Что ж, обо всём по порядку. Начнём с первого вопроса. Что означают все эти индексы? И как не ошибиться при работе с реальными матрицами?
Данный процесс легко понять по картинке:
Схема перемножения двух матриц
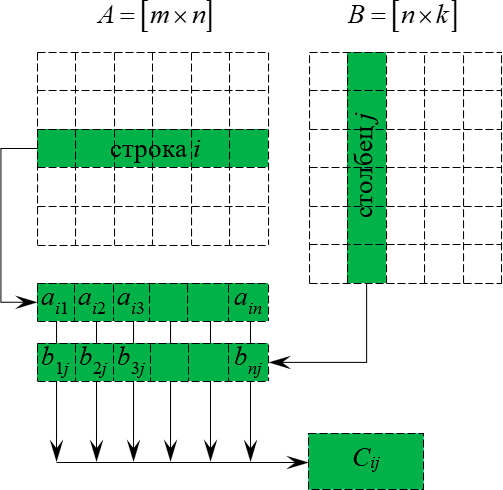
На самом деле мы уже встречались с перемножением матриц в школьной программе, только в сильно урезанном виде. Пусть даны вектора:
Тогда их скалярным произведением будет именно сумма попарных произведений:
Сегодня ничего не поменялось. Просто теперь этих векторов-строк и столбцов стало больше.
Но хватит теории! Давайте посмотрим на реальные примеры. И начнём с самого простого случая — квадратных матриц.
Умножение квадратных матриц
Задача 2. Выполните умножение:
Решение. Опять согласованные матрицы, поэтому выполняем действия:\[\]
Как видим, получилась матрица, заполненная нулями
Из приведённых примеров очевидно, что умножение матриц — не такая уж и сложная операция. По крайней мере для квадратных матриц размера 2 на 2.
В процессе вычислений мы составили промежуточную матрицу, где прямо расписали, какие числа входят в ту или иную ячейку. Именно так и следует делать при решении настоящих задач.
Основные свойства матричного произведения
В двух словах. Умножение матриц:
А теперь — всё то же самое, но более подробно.
Умножение матриц во многом напоминает классическое умножение чисел. Но есть отличия, важнейшее из которых состоит в том, что умножение матриц, вообще говоря, некоммутативно.
Рассмотрим ещё раз матрицы из задачи 1. Прямое их произведение мы уже знаем:
Но если поменять матрицы местами, то получим совсем другой результат:
Тем не менее, умножение матриц ассоциативно:
\[\left( A\cdot B \right)\cdot C=A\cdot \left( B\cdot C \right)\]
Следовательно, когда вам надо перемножить сразу несколько матриц подряд, совсем необязательно делать это напролом: вполне возможно, что некоторые рядом стоящие матрицы при перемножении дают интересный результат. Например, нулевую матрицу, как в Задаче 2, рассмотренной выше.
Такая матрица всегда выглядит одинаково: на главной диагонали её стоят единицы, а во всех остальных клетках — нули.
Идём далее. Помимо ассоциативности умножение матриц ещё и дистрибутивно:
Другими словами, если нужно умножить одну матрицу на сумму двух других, то можно умножить её на каждую из этих «двух других», а затем результаты сложить. На практике обычно приходится выполнять обратную операцию: замечаем одинаковую матрицу, выносим её за скобку, выполняем сложение и тем самым упрощаем себе жизнь.:)
Заметьте: для описания дистрибутивности нам пришлось прописать две формулы: где сумма стоит во втором множителе и где сумма стоит в первом. Это происходит как раз из-за того, что умножение матриц некоммутативно (и вообще, в некоммутативной алгебре куча всяких приколов, которые при работе с обычными числами даже не приходят в голову). И если, допустим, вам на экзамене нужно будет расписать это свойство, то обязательно пишите обе формулы, иначе препод может немного разозлиться.
Ладно, всё это были сказки о квадратных матрицах. А что насчёт прямоугольных?
Случай прямоугольных матриц
А ничего — всё то же самое, что и с квадратными.
Сейчас рассмотрим одно из лучших тренировочных заданий для тех, кто только начинает работать с матрицами. В нём нужно не просто перемножить какие-то две таблички, а сначала определить: допустимо ли такое умножение?
Рекомендую после прочтения задания не смотреть в решение, а сначала попробовать выполнить его самостоятельно. И затем сравнить с ответами.
Задача 4. Найдите все возможные попарные произведения матриц:
Решение. Для начала запишем размеры матриц:
\[A=\left[ 2\times 4 \right];\ B=\left[ 4\times 2 \right];\ C=\left[ 2\times 2 \right]\]
Промежуточные шаги предлагаю выполнить читателю самостоятельно. Замечу лишь, что размер результирующей матрицы лучше определять заранее, ещё до каких-либо вычислений:
\[A \cdot B=\left[ 2\times 4 \right]\cdot \left[ 4\times 2 \right]=\left[ 2\times 2 \right]\]
Другими словами, мы просто убираем «транзитные» коэффициенты, которые обеспечивали согласованность матриц.
\[B \cdot A=\left[ 4\times 2 \right]\cdot \left[ 2\times 4 \right]=\left[ 4\times 4 \right]\]
\[B\cdot C=\left[ \begin
Вообще, очень рекомендую выполнить это задание самостоятельно. И ещё одно аналогичное задание, которое есть в домашней работе. Эти простые на первый взгляд размышления помогут вам отработать все ключевые этапы умножения матриц.
Но на этом история не заканчивается. Переходим к частным случаям умножения.:)
Вектор-строки и вектор-столбцы
Одной из самых распространённых матричных операций является умножение на матрицу, в которой одна строка или один столбец.
Задача 6. Выполните умножение:
На самом деле мне было в лом считать все эти три числа — посчитайте сами. А я просто запишу ответ.:)
Как видите, при умножении вектор-строки и вектор-столбца на квадратную матрицу на выходе мы всегда получаем строку или столбец того же размера. Этот факт имеет множество приложений — от решения линейных уравнений до всевозможных преобразований координат (которые в итоге тоже сводятся к системам уравнений, но давайте не будем о грустном).
Думаю, здесь всё было очевидно. Переходим к заключительной части сегодняшнего урока.
Возведение матрицы в степень
Среди всех операций умножения отдельного внимания заслуживает возведение в степень — это когда мы несколько раз умножаем один и тот же объект на самого себя. Матрицы — не исключение, их тоже можно возводить в различные степени.
Такие произведения всегда согласованы:
\[A\cdot A=\left[ n\times n \right]\cdot \left[ n\times n \right]=\left[ n\times n \right]\]
И обозначаются точно так же, как и обычные степени:
На первый взгляд, всё просто. Посмотрим, как это выглядит на практике:
Задача 7. Возведите матрицу в указанную степень:
Решение. Ну ОК, давайте возводить. Сначала возведём в квадрат:
\[\begin
\[\begin
Задача 8. Возведите матрицу в указанную степень:
Решение. Вот только не надо сейчас плакать по поводу того, что «степень слишком большая», «мир не справедлив» и «преподы совсем берега потеряли». На самом деле всё легко:
\[\begin
Заметьте: во второй строчке мы использовали ассоциативность умножения. Собственно, мы использовали её и в предыдущем задании, но там это было неявно.
Как видите, ничего сложного в возведении матрицы в степень нет. Последний пример можно обобщить:
Этот факт легко доказать через математическую индукцию или прямым перемножением. Однако далеко не всегда при возведении в степень можно выловить подобные закономерности. Поэтому будьте внимательны: зачастую перемножить несколько матриц «напролом» оказывается проще и быстрее, нежели искать какие-то там закономерности.
Задача 9. Возведите матрицу в указанную степень:
Решение. Не будем искать закономерности. Работаем «напролом»:
\[ <<\left[ \begin
Для начала возведём эту матрицу в квадрат:
\[\begin
Теперь возведём в куб:
\[\begin
Вот и всё. Задача решена.
Как видите, объём вычислений стал больше, но смысл от этого нисколько не поменялся.:)
На этом урок можно заканчивать. В следующий раз мы рассмотрим обратную операцию: по имеющемуся произведению будем искать исходные множители.
Как вы уже, наверное, догадались, речь пойдёт об обратной матрице и методах её нахождения.
Умножение матриц: примеры, алгоритм действий, свойства произведения
Произведение двух матриц
Произведение матриц (С= АВ) — операция только для согласованных матриц А и В, у которых число столбцов матрицы А равно числу строк матрицы В:
C ⏟ m × n = A ⏟ m × p × B ⏟ p × n
Вычислим произведения АВ=ВА:
Решение, используя правило умножения матриц:
А ⏟ 2 × 3 × В ⏟ 3 × 2 = 1 2 1 0 1 2 × 1 0 0 1 1 1 = 1 × 1 + 2 × 0 + 1 × 1 1 × 0 + 2 × 1 + 1 × 1 0 × 1 + 1 × 0 + 2 × 1 0 × 0 + 1 × 1 + 2 × 1 = = 2 3 2 3 ⏟ 2 × 2
В ⏟ 3 × 2 × А ⏟ 2 × 3 = 1 0 0 1 1 1 × 1 2 1 0 1 2 = 1 × 1 + 0 × 0 1 × 2 + 0 × 1 1 × 1 + 0 × 2 0 × 1 + 1 × 0 0 × 2 + 1 × 1 0 × 1 + 1 × 2 1 × 1 + 1 × 0 1 × 2 + 1 × 1 1 × 1 + 1 × 2 = 1 2 1 0 1 2 1 3 3 ⏟ 3 × 3
Свойства умножения матриц
Свойства умножения матриц:
Проверяем свойство №1: ( А В ) С = А ( В С ) :
Проверяем свойство №2: А ( В + С ) = А В + А С :
Произведение трех матриц
Произведение трех матриц А В С вычисляют 2-мя способами:
Перемножить матрицы 2-мя способами:
Алгоритм действий:
Используем формулу А В С = ( А В ) С :
Умножение матрицы на число
Произведение матрицы А на число k — это матрица В = А k того же размера, которая получена из исходной умножением на заданное число всех ее элементов:
Свойства умножения матрицы на число:
Найдем произведение матрицы А = 4 2 9 0 на 5.
5 А = 5 4 2 9 0 5 × 4 5 × 2 5 × 9 5 × 0 = 20 10 45 0
Умножение матрицы на вектор
Чтобы найти произведение матрицы и вектора, необходимо умножать по правилу «строка на столбец»:
А В = а 11 а 12 ⋯ а 1 n а 21 а 22 ⋯ а 2 n ⋯ ⋯ ⋯ ⋯ а m 1 а m 2 ⋯ а m n b 1 b 2 ⋯ b 1 n = a 11 × b 1 + a 12 × b 2 + ⋯ + a 1 n × b n a 21 × b 1 + a 22 × b 2 + ⋯ + a 2 n × b n ⋯ ⋯ ⋯ ⋯ a m 1 × b 1 + a m 2 × b 2 + ⋯ + a m n × b n = c 1 c 2 ⋯ c 1 m
А В = а а ⋯ а b b ⋯ b = a 1 × b 1 a 1 × b 2 ⋯ a 1 × b n a 2 × b 1 a 2 × b 2 ⋯ a 2 × b n ⋯ ⋯ ⋯ ⋯ a n × b 1 a n × b 2 ⋯ a n × b n = c 11 c 12 ⋯ c 1 n c 21 c 22 ⋯ c 2 n ⋯ ⋯ ⋯ ⋯ c n 1 c n 2 ⋯ c n n
Найдем произведение матрицы А и вектора-столбца В :
Найдем произведение матрицы А и вектора-строку В :
Действия с матрицами
Данное методическое пособие поможет Вам научиться выполнять действия с матрицами: сложение (вычитание) матриц, транспонирование матрицы, умножение матриц, нахождение обратной матрицы. Весь материал изложен в простой и доступной форме, приведены соответствующие примеры, таким образом, даже неподготовленный человек сможет научиться выполнять действия с матрицами. Для самоконтроля и самопроверки Вы можете бесплатно скачать матричный калькулятор >>>.
Я буду стараться минимизировать теоретические выкладки, кое-где возможны объяснения «на пальцах» и использование ненаучных терминов. Любители основательной теории, пожалуйста, не занимайтесь критикой, наша задача – научиться выполнять действия с матрицами.
Для СВЕРХБЫСТРОЙ подготовки по теме (у кого «горит») есть интенсивный pdf-курс Матрица, определитель и зачёт!
Матрица – это прямоугольная таблица каких-либо элементов. В качестве элементов мы будем рассматривать числа, то есть числовые матрицы. ЭЛЕМЕНТ – это термин. Термин желательно запомнить, он будет часто встречаться, не случайно я использовал для его выделения жирный шрифт.
Обозначение: матрицы обычно обозначают прописными латинскими буквами 
Пример: рассмотрим матрицу «два на три»:
Данная матрица состоит из шести элементов: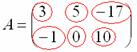 
Все числа (элементы) внутри матрицы существуют сами по себе, то есть ни о каком вычитании речи не идет: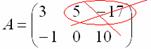 
Это просто таблица (набор) чисел!
Также договоримся не переставлять числа, если иного не сказано в объяснениях. У каждого числа свое местоположение, и перетасовывать их нельзя!
Рассматриваемая матрица имеет две строки: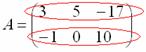 
и три столбца: 
СТАНДАРТ: когда говорят о размерах матрицы, то сначала указывают количество строк, а только потом – количество столбцов. Мы только что разобрали по косточкам матрицу «два на три».
Если количество строк и столбцов матрицы совпадает, то матрицу называют квадратной, например: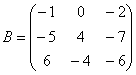 
– матрица «три на три».
Если в матрице один столбец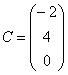 
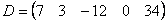
или одна строка 
, то такие матрицы также называют векторами.
На самом деле понятие матрицы мы знаем еще со школы, рассмотрим, например точку с координатами «икс» и «игрек»: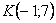 
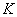
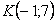
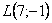
. По существу, координаты точки 
записаны в матрицу «один на два». Кстати, вот Вам и пример, почему порядок чисел имеет значение: 
и 
– это две совершенно разные точки плоскости.
Теперь переходим непосредственно к изучению действий с матрицами:
1) Действие первое. Вынесение минуса из матрицы (внесение минуса в матрицу).
Вернемся к нашей матрице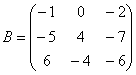 
. Как вы наверняка заметили, в данной матрице слишком много отрицательных чисел. Это очень неудобно с точки зрения выполнения различных действий с матрицей, неудобно писать столько минусов, да и просто в оформлении некрасиво выглядит.
Вынесем минус за пределы матрицы, сменив у КАЖДОГО элемента матрицы знак: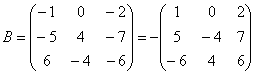 
У нуля, как Вы понимаете, знак не меняется, ноль – он и в Африке ноль.
Обратный пример: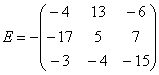 
. Выглядит безобразно.
Внесем минус в матрицу, сменив у КАЖДОГО элемента матрицы знак:
Ну вот, гораздо симпатичнее получилось. И, самое главное, выполнять какие-либо действия с матрицей будет ПРОЩЕ. Потому что есть такая математическая народная примета: чем больше минусов – тем больше путаницы и ошибок.
2) Действие второе. Умножение матрицы на число.
Всё просто, для того чтобы умножить матрицу на число, нужно каждый элемент матрицы умножить на данное число. В данном случае – на тройку.
Еще один полезный пример:
– умножение матрицы на дробь
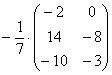
Сначала рассмотрим то, чего делать НЕ НАДО: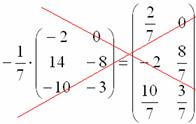 
Вносить дробь в матрицу НЕ НУЖНО, во-первых, это только затрудняет дальнейшие действия с матрицей, во-вторых, затрудняет проверку решения преподавателем (особенно, если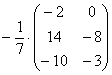 
– окончательный ответ задания).
И, тем более, НЕ НАДО делить каждый элемент матрицы на минус семь:
Из статьи Математика для чайников или с чего начать, мы помним, что десятичных дробей с запятой в высшей математике стараются всячески избегать.
Единственное, что желательно сделать в этом примере – это внести минус в матрицу:
А вот если бы ВСЕ элементы матрицы делились на 7 без остатка, то тогда можно (и нужно!) было бы поделить.
В этом случае можно и НУЖНО умножить все элементы матрицы на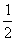 
, так как все числа матрицы делятся на 2 без остатка.
Примечание: в теории высшей математики школьного понятия «деление» нет. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». То есть, деление – это частный случай умножения.
3) Действие третье. Транспонирование матрицы.
Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.
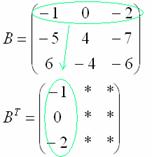
Транспонировать матрицу 
Строка здесь всего одна и, согласно правилу, её нужно записать в столбец:
– транспонированная матрица.
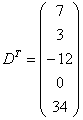
Транспонированная матрица обычно обозначается надстрочным индексом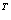 
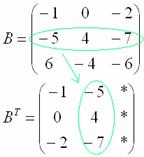
или штрихом справа вверху.
Транспонировать матрицу 
Сначала переписываем первую строку в первый столбец:
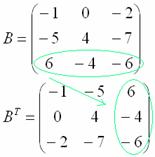
Потом переписываем вторую строку во второй столбец: 
И, наконец, переписываем третью строку в третий столбец:
Готово. Образно говоря, транспонировать – это значит взять матрицу за правый верхний угол и аккуратно повернуть её «на себя» по диагонали, «стряхивая» числа в столбцы транспонированной матрицы. Такая вот у меня ассоциация.
4) Действие четвертое. Сумма (разность) матриц.
Сумма матриц действие несложное.
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.
Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой! 
Сложить матрицы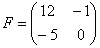 
и 
Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:
Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов.
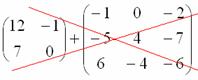
Найти разность матриц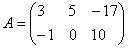 
, 
А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу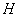 
:
Примечание: в теории высшей математики школьного понятия «вычитание» нет. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.
5) Действие пятое. Умножение матриц.
Чем дальше в лес, тем толще партизаны. Скажу сразу, правило умножения матриц выглядит очень странно, и объяснить его не так-то просто, но я все-таки постараюсь это сделать, используя конкретные примеры.
Какие матрицы можно умножать?
Чтобы матрицу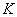 
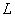
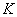
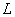
можно было умножить на матрицу 
нужно, чтобы число столбцов матрицы 
равнялось числу строк матрицы 
.
Пример:
Можно ли умножить матрицу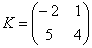 
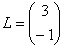
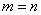
на матрицу 
?
, значит, умножать данные матрицы можно.
А вот если матрицы переставить местами, то, в данном случае, умножение уже невозможно!
, следовательно, выполнить умножение невозможно:
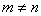
Не так уж редко встречаются задания с подвохом, когда студенту предлагается умножить матрицы, умножение которых заведомо невозможно.
Следует отметить, что в ряде случаев можно умножать матрицы и так, и так.
Например, для матриц,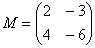 
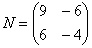
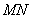
и 
возможно как умножение 
, так и умножение 
Как умножить матрицы?
Умножение матриц лучше объяснить на конкретных примерах, так как строгое определение введет в замешательство (или помешательство) большинство читателей.
Начнем с самого простого:
Умножить матрицу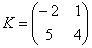 
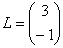
на матрицу 
Я буду сразу приводить формулу для каждого случая:
– попытайтесь сразу уловить закономерность.
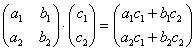
Умножить матрицу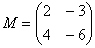 
на матрицу 
Формула: 
В результате получена так называемая нулевая матрица.
Попробуйте самостоятельно выполнить умножение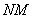 
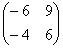
(правильный ответ 
).
Обратите внимание, что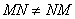 
! Это почти всегда так!
Таким образом, при умножении переставлять матрицы нельзя!
Если в задании предложено умножить матрицу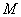 
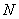
на матрицу 
, то и умножать нужно именно в таком порядке. Ни в коем случае не наоборот.
Переходим к матрицам третьего порядка:
Умножить матрицу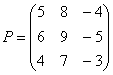 
на матрицу 
Формула очень похожа на предыдущие формулы: 
А теперь попробуйте самостоятельно разобраться в умножении следующих матриц:
Умножьте матрицу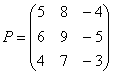 
на матрицу 
Вот готовое решение, но постарайтесь сначала в него не заглядывать!
Данная тема достаточно обширна, и я вынес этот пункт на отдельную страницу.
А пока спектакль закончен.
После освоения начального уровня рекомендую отработать действия с матрицами на уроке Свойства операций над матрицами. Матричные выражения.
Автор: Емелин Александр
(Переход на главную страницу)
Zaochnik.com – профессиональная помощь студентам
cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5
Tutoronline.ru – онлайн репетиторы по математике и другим предметам