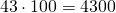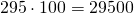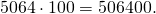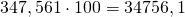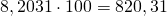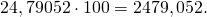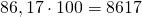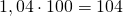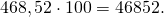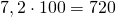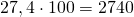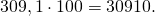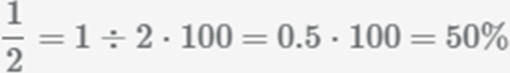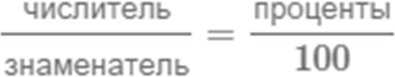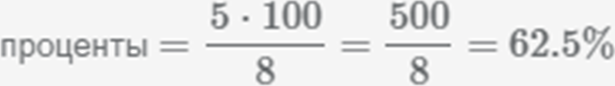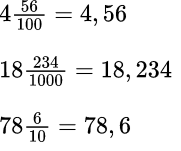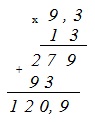Как умножить дробь на 100
Калькулятор дробей
Как перевести смешанную дробь в обыкновенную
Для того, чтобы перевести смешанную дробь в обыкновенную, необходимо к числителю дроби прибавить произведение целой части и знаменателя: i n d = i · d + n d
5 3 4 = 5 · 4 + 3 4 = 23 4
Как перевести обыкновенную дробь в смешанную
Для того, чтобы перевести обыкновенную дробь в смешанную, необходимо:
Как перевести обыкновенную дробь в десятичную
Для того, чтобы перевести обыкновенную дробь в десятичную, нужно разделить её числитель на знаменатель.
Как перевести десятичную дробь в обыкновенную или смешанную
Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо:
Например, переведем 0.36 в обыкновенную дробь:
Как перевести дробь в проценты
Для того, чтобы перевести обыкновенную или смешанную дробь в проценты, необходимо перевести её в десятичную дробь и умножить на 100.
Как перевести проценты в дробь
Для того, чтобы перевести проценты в дробь, необходимо получить из процентов десятичную дробь (разделив на 100), затем полученную десятичную дробь перевести в обыкновенную.
Сложение дробей
Алгоритм действий при сложении двух дробей такой:
Вычитание дробей
Алгоритм действий при вычитании двух дробей:
Умножение дробей
Алгоритм действий при умножении двух дробей:
Деление дробей
Алгоритм действий при делении двух дробей:
Как умножать на 100
Повторим, как умножать на 100 натуральные числа и десятичные дроби.
Правило умножения на 100 натурального числа
Чтобы умножить на 100 натуральное число, надо в его записи справа приписать два нуля.
Правило умножения на 100 десятичной дроби
Чтобы умножить на 100 десятичную дробь, надо в ее записи перенести запятую на две цифры вправо.
При умножении на 100 десятичной дроби с двумя знаками после запятой получаем натуральное число:
При умножении на 100 десятичной дроби с одним знаком после запятой, перенеся запятую вправо на два знака, получаем натуральное число, запись которого заканчивается нулем:
Умножать на 100 обыкновенную дробь нужно по правилу умножения дроби на число.
Смешанное число умножить на 100 можно любым из двух способов.
Как превратить обыкновенную дробь в проценты и наоборот.
Процент – название, принятое во всем мире.
Превратить обыкновенную дробь в проценты и наоборот можно несколькими способами.
1 способ.
Мы умеем превращать десятичные дроби в проценты и наоборот.
1. 1/2 превращаем в проценты.
1/2 превратим в десятичную – 1/2 = 5/10 = 0,5.
Теперь 0,5 умножим на 100, получим – 50%.
2. 5/8 превращаем в проценты.
5/8 превратим в десятичную – 5/8 = 625/1000 = 0,625.
Теперь 0,625 умножим на 100, получим – 62,5%.
2 способ.
1. 1⁄2 превращаем в проценты.
1⁄2 превратим в десятичную, для этого 1 разделим на 2 = 0,5.
Теперь 0,5 умножим на 100, получим – 50%.
2. 15/32 превращаем в проценты.
15/32 превратим в десятичную, для этого 15 разделим на 32 = 0,46875.
Теперь 0,46875 умножим на 100, получим – 46,875%.
3 способ.
Способ 2 (см. выше), превратим в пропорцию.
5/8 превращаем в проценты.

Каждый из вас выберет более УДОБНЫЙ для себя способ.
Для превращения процентов в обыкновенную дробь, действуем наоборот.
1 способ.
1. 17,8% превратим в десятичную дробь.
17,8 делим на 100, получаем 17,8 : 100 = 0,178.
Теперь 178/1000 сократим дробь на 2, получим 89/500.
2. 96% превратим в десятичную дробь: 96/100.
Сокращаем на 4, получим 24/25.
2 способ.
20,125% превратим в обыкновенную дробь.
20,125 делим 100.
Получим 20,125/100.
Т.к. 20,125 не целое число, поэтому умножаем его на 1000. Тогда, чтобы дробь не изменилась, знаменатель – 100 тоже умножим на 1000.
Получим дробь — 20125/100000.
Сократим на 125 = 161/800.
Каждый выберет УДОБНЫЙ для себя способ.
Также можете воспользоваться памяткой в статье «Как перевести десятичную дробь в проценты?».
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 5 / 5. Количество оценок: 71
Десятичные дроби
теория по математике 📈 числа и вычисления
Десятичная дробь — дробь, которая представляет собой способ представление числа в виде записи числа с запятой, где цифры перед запятой называются целой частью, а цифры после запятой – дробной частью (десятичной частью).
Десятичные дроби получают из записи обыкновенных дробей со знаменателем 10, 100, 1000 и так далее. Например, десятичные дроби:
4,56 – четыре целых пятьдесят шесть сотых 18,234 – восемнадцать целых двести тридцать четыре тысячных 78,6 – семьдесят восемь целых шесть десятых
Чтение десятичных дробей
Чтение десятичной части (десятых, сотых и так далее) зависит от количества цифр после запятой. Если цифра одна, то читают – десятых (в числе десять — один нуль, это соответствует одной цифре). Если две цифры после запятой, то читают – сотых (в сотне два нуля).
Десятичные дроби получаются из обыкновенных дробей:
Сложение (вычитание) десятичных дробей
Чтобы сложить (вычесть) в столбик две десятичные дроби нужно:
Если складывают (вычитают) целое число и десятичную дробь, то нужно поставить запятую после целого числа и приписать необходимое количество нулей после запятой.
Пример №1. Запись, где запятая под запятой и соответствующий разряд под соответствующим.
34,145 + 5,678 = 39,823
Пример №2. Запись, где также запятая под запятой, а во втором числе дописан нуль, чтобы уравнять количество знаков после запятой.
Пример №3. В первом слагаемом нет десятичной части, поэтому, после числа 56 поставили запятую и добавили нужное количество нулей.
Умножение десятичных дробей
При умножении двух десятичных дробей в столбик необходимо:
Пример №4. Запись выполнена так, что цифры по правому краю записаны ровно одна под одной, то есть как при обычном умножении чисел в столбик. Умножение выполнено без учета запятой. В ответе справа отделены 4 цифры запятой, так как в первом множителе их 3 после запятой, а во втором – одна, в двух множителях вместе – четыре.
0,125 × 2,3 00375 0250 0,2875
Пример №5. Здесь показано умножение десятичной дроби и целого числа. Умножение выполнено без учета запятой. В ответе отделена справа запятой только одна цифра, так как только в первом множителе есть десятичная часть с одной цифрой после запятой.
Умножение десятичных дробей на 10, 100, 1000…
Чтобы умножить десятичную дробь на 10, 100, 1000 и так далее, нужно перенести запятую вправо на столько цифр, сколько нулей у множителя. Умножение в данном случае выполняется в строчку.
Пример №6. 2,456 × 10 = 24,56 Запятую в десятичной дроби перенесли вправо на 1 цифру, так как у 10 один нуль.
Пример №7. 0,45678 × 100 = 45,678 Запятую перенесли вправо на 2 цифры, так как у 100 два нуля. Нуль, стоящий в начале десятичной дроби, убрали, так как впереди целой части, отличной от нуля он не пишется.
Пример №8. 9,46 × 1000 = 9460 в данном случае при переносе запятой на три цифра не хватило одной, поэтому в конце числа приписали нуль, и в ответе получилось целое число.
Умножение десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…
При умножении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 (и так далее) нужно перенести запятую на столько цифр влево, сколько цифр в данной разрядной единице после запятой. Умножение обычно выполняется в строчку устно.
Пример №9. 983,7821 × 0,01= 9,837821 Переносим запятые влево на 2 цифры, так как в числе 0,01 две цифры после запятой.
Пример №10. 8,7654 × 0,1 = 0,87654 Перенесли на 1 цифру влево, так как в числе 0,1 одна цифра после запятой. В данном случае перед 8 появился нуль, так как при переносе запятой слева цифр не оказалось.
Пример №11. 7,98 × 0,0001 = 0,000798 При переносе влево на 4 цифры не хватило трех, поэтому впереди поставили нули, а также нуль образуется и в целой части.
Деление десятичных дробей
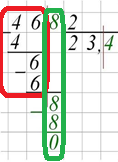
Пример №12. Деление десятичной дроби на целое число. 46,8 : 2 = 23,4
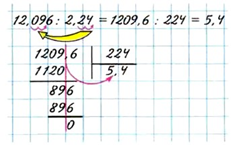
Пример №13. Деление десятичной дроби на десятичную дробь. 12,096 : 2,24 = 5,4 Из данного примера видно, что деление десятичных дробей обязательно сводится к делению на целое число.
Пример №14. 276,3 : 0,003 = 276300 : 3 = 92100. Здесь видно, что не хватает двух цифр в числе 276,3 и поэтому при переносе запятой к нему приписали два нуля. Затем выполнили деление двух целых чисел.
Деление десятичной дроби на 10, 100, 1000…
При делении десятичной дроби на 10,100, 1000 и так далее нужно перенести запятую на столько цифр влево, сколько нулей в данном числе. Деление выполняется в строчку устно.
Пример №16. 134,987 : 1000 = 0,134987 Перенесли запятую на три цифры влево, так как у 1000 три нуля. В целой части поставили нуль, так как цифр не хватило.
Пример №17. 7,234 : 100 = 0,07234 Перенесли запятую влево на две цифры. Так как цифр не хватало, то недостающие заменили нулями.
Деление десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…
При делении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 и так далее нужно перенести запятую на столько цифр вправо, сколько цифр в данной разрядной единице после запятой. Деление обычно выполняется в строчку устно.
Пример №19. 41,234 : 0,01 = 4123,4 Перенос запятой на 2 цифры вправо, так как в числе 0,01 две цифры после запятой.
Пример №20. 56,91 : 0,001 = 56910 При переносе запятой на три цифры вправо приписали один нуль, так как одной цифры не хватило.
Сформируем из чисел ряд от наименьшего из них до наибольшего. Для этого сначала разделим их на положительные и отрицательные. И сразу получим наибольшее в ряду (поскольку оно единственное больше нуля): 0,021.
Три оставшихся отрицательных распределим по их модулям. Известно, что из двух отрицательных чисел больше то, у которого модуль меньше. Тогда получаем, что –0,304
pазбирался: Даниил Романович | обсудить разбор | оценить
Для получения результата необходимо последовательно выполнить математические действия в соответствии с их приоритетом.
Выполняем возведение в степень. Получаем числа, состоящие из единицы и следующего за ней количества нулей, равного показателю степени. При этом знаки «–» в скобках исчезают, поскольку показатели степеней четные. Получаем:
Выполняем умножение. Для этого в числе 0,3 переносим десятичную запятую на 4 знака вправо (так как в 10000 четыре нуля), а к 4 дописываем, соответственно, 2 нуля. Получаем:
Выполняем сложение –3000+400. Поскольку это числа с разными знаками, то вычитаем из большего модуля меньший и перед результатом ставим «–», поскольку число с большим модулем отрицательное. Получаем:
Так как оба числа отрицательные, то складываем их модули и перед результатом ставим «–». Получаем:
pазбирался: Даниил Романович | обсудить разбор | оценить
Это задание требует простого умения выполнять арифметические действия с десятичными дробями.
Сначала выполняем умножение. Умножаем –13 и –9,3 в столбик без учета знаков «–» перед сомножителями. В полученном произведении отделяем одну – последнюю – цифру десятичной запятой:
Знак произведения будет положительным, поскольку умножаются два отрицательных числа. Получаем:
Эту разность можно вычислить в столбик, но можно и устно. Выполним это действие в уме: вычитаем отдельно целые части и десятичные. Получаем:
pазбирался: Даниил Романович | обсудить разбор | оценить
Задачу можно решать разными путями, а именно менять последовательность действий, но этот вариант решения рекомендуется для тех, кто уверен в своих возможностях и знает математику на отлично. Для остальных мы рекомендуем выполнить последовательно действия в числителе и знаменателе, а затем разделить числитель на знаменатель. Числитель вычислять в данном примере нет необходимости, это число 9.
Вычислим значение знаменателя:
Можно произвести вычисления в столбик, тогда получим:
Либо перевести дробь к простому виду:
4,5 • 2,5 = 4½ • 2 ½ = 9 / 2 • 5 / 2 = 45 / 4
Последний случай предпочтительней, так как для дальнейшей операции — деления числителя на знаменатель задача упрощается. Делим числитель на знаменатель, умножая числитель на перевернутую дробь в знаменателе:
9 / ( 45 / 4 ) = ( 9 / 1 ) • ( 4 / 45 ) = ( 9 • 4 ) / (1 • 45 )
9 и 45 можно сократить на 9:
( 9 • 4 ) / (1 • 45 ) = ( 1 • 4 )/ (1 • 5 ) = 4 / 5 = 8 / 10 = 0,8
pазбирался: Даниил Романович | обсудить разбор | оценить
Как умножить дробь на 100
Чтобы умножить натуральное число на множитель 10, 100, 1000 и так далее, достаточно приписать к числу справа столько нулей, сколько их в множителе.
Умножение десятичных дробей на 10, 100, 1000…
Чтобы умножить десятичную дробь на множитель 10, 100, 1000 и так далее, нужно в этой дроби перенести запятую на столько цифр вправо, сколько нулей содержится в множителе.
Если количество цифр в дробной части равно количеству нулей в множителе, то запятая просто отбрасывается и получается целое число.
| Пример: 8,902 · 1000 = 8902. |
Если количество цифр в дробной части меньше количества нулей в множителе, то запятая отбрасывается, а вместо недостающих знаков справа приписываем нули.
Пример: 71,13 · 10000
В множителе 10000 – четыре нуля, поэтому нужно перенести запятую вправо на четыре знака. Но у нас в дробной части только две цифры, значит, необходимо отбросить запятую и дописать два нуля справа.
71,13 · 10000 = 711300.
Умножение на круглое число
Назовем круглым числом такое число, у которого все цифры, кроме старшего разряда, нули.
Умножаем 57 на 3 и к произведению приписываем справа два нуля, получаем:
Умножение на 0,1; 0,01; 0, 001…
Чтобы умножить натуральное число на множитель 0,1; 0,01; 0, 001 и так далее, нужно отсчитать в числе справа столько же знаков, сколько нулей в множителе, и поставить запятую.
В множителе 0,1 один нуль, значит, чтобы найти произведение, нужно отсчитать в числе 372 справа один знак и поставить запятую.
В множителе 0,001 три нуля, значит, чтобы найти произведение, нужно отсчитать в числе 3074 справа три знака и поставить запятую.
Если количество знаков в числе равно количеству нулей в множителе, то слева от числа ставим запятую и пишем в целой части нуль.
Если в числе меньше знаков, чем нулей в множителе, то слева к числу дописываем столько нулей, сколько не хватило знаков, ставим запятую и пишем в целой части нуль.