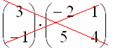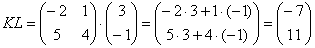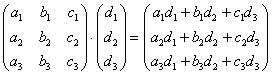Как умножаются матрицы 2х2

Матричное умножение. Медленное достижение мифической цели

В недавней работе был установлен новый рекорд скорости по умножению двух матриц. Она также знаменует и конец эпохи для метода, который ученые применяли для исследований на протяжении десятилетий.

Математики стремятся к достижению мифической цели — второй степени (exponent two), то есть к умножению пары матриц n х n всего за n 2 шагов. Исследователи подбираются все ближе к своей цели, но получится ли у них когда-нибудь достичь ее?

Для специалистов в области Computer Science и математиков сама идея о «второй степени» связана с представлениями о совершенном мире.

«Трудно разграничить научное мышление и беспочвенные мечтания», — признается Крис Уманс из Калифорнийского технологического института. «Я хочу, чтобы степень была равна двум, потому что это красиво».

С точки зрения необходимого количества шагов «вторая степень» — это идеальная скорость выполнения одной из самых фундаментальных математических операций — матричного умножения. Если вторая степень достижима, то матричное умножение получится выполнять максимально быстро, насколько это физически возможно. Если это не так, то мы застряли в мире, который не соответствует нашим мечтам.

Матрицы представляют собой массивы чисел. Когда две матрицы согласованы (число столбцов в первом сомножителе равно числу строк во втором), их можно перемножить, чтобы получить третью. Например, если вы начнете с пары матриц 2 х 2, их произведение также будет матрицей 2 х 2, содержащей четыре элемента. В более общем смысле, произведение пары матриц размером n х n представляет собой другую матрицу размером n х n с n 2 элементами.

И хотя никто точно не знает, можно ли этого достичь, исследователи продолжают продвигаться в этом направлении.

Статья, опубликованная в октябре, подбирается к цели еще ближе и описывает самый быстрый на данный момент метод умножения двух матриц. Результат, который получили Джош Алман, докторант Гарвардского университета, и Вирджиния Василевска Уильямс из Массачусетского технологического института, уменьшает степень предыдущего лучшего показателя примерно на одну стотысячную. Это действительно большое достижение в данной области, добытое кропотливым трудом.

Чтобы получше разобраться в этом процессе и понять, как его можно усовершенствовать, давайте начнем с пары матриц 2 х 2, A и B. При вычислении каждого элемента их произведения вы используете соответствующую строку из A и соответствующий столбец из B. Чтобы получить верхний правый элемент, умножьте первое число в первой строке A на первое число во втором столбце B, затем умножьте второе число в первой строке A на второе число во втором столбце B и сложите эти два произведения.

Самуэль Веласко / Quanta Magazine

Эта операция известна как получение «скалярного произведения» строки со столбцом (иногда называется «внутренним произведением»). Чтобы вычислить другие элементы в произведении матриц, повторите процедуру с соответствующими строками и столбцами.

В целом, классический метод умножения матриц 2 х 2 состоит из восьми умножений и нескольких сложений. Как правило, этот способ умножения двух матриц размера n х n требует n 3 умножений.

С увеличением размера матриц количество умножений, необходимых для нахождения их произведения, растет намного быстрее, чем количество сложений. Чтобы найти произведение матриц 2 х 2 требуется всего восемь промежуточных умножений, а чтобы найти произведение матриц 4 х 4 их требуется уже 64. Однако количество сложений, необходимых для получения суммы этих матриц, не так значительно отличается. Обычно количество сложений равно количеству элементов в матрице, то есть четыре для матриц 2 х 2 и 16 для матриц 4 х 4. Эта разница между сложением и умножением позволяет понять, почему исследователи измеряют скорость умножения матриц исключительно с точки зрения количества требуемых умножений.

«Умножения — это наше всё, — утверждает Уманс, — Показатель степени в итоге полностью зависит только от количества умножений. Сложения в некотором смысле исчезают».

На протяжении веков люди считали, что n 3 — это самый быстрый способ умножения матриц. По имеющимся сведениям, в 1969 году Фолькер Штрассен намеревался доказать, что невозможно умножить матрицы 2 х 2, используя менее восьми умножений. Видимо, он все-таки не смог найти доказательства, а через некоторое время и понял почему: на самом деле, существует способ сделать это с помощью семи умножений!

Штрассен придумал сложный набор соотношений, которые позволили заменить одно из этих восьми умножений 14 дополнительными сложениями. Может показаться, что разница совершенно незначительна, но она оправдывает себя, так как умножение вносит больший вклад, чем сложение. Найдя способ избавиться от одного умножения для маленьких матриц 2 х 2, Штрассен открыл возможность, которую он мог использовать при умножении бOльших матриц.

«Это крошечное изменение приводит к огромным улучшениям в работе с большими матрицами», — говорит Уильямс.

Вирджиния Василевска Уильямс из Массачусетского технологического института и Джош Алман из Гарвардского университета открыли самый быстрый способ перемножения двух матриц за n 2.3728596 шагов. Джаред Чарни; Ричард Т.К. Хоук

Предположим, вы хотите перемножить пару матриц 8 х 8. Один из способов сделать это — разбить каждую большую матрицу на четыре матрицы размером 4 х 4 так, чтобы каждая имела по четыре элемента. Поскольку элементы матрицы также могут являться матрицами, вы можете считать исходные матрицы парой матриц 2 х 2, каждый из четырех элементов которых сам по себе является матрицей 4 х 4. Посредством некоторых манипуляций каждая из этих матриц размером 4 х 4 может быть разбита на четыре матрицы размером 2 х 2.

Смысл этого многократного разбиения больших матриц на более мелкие заключается в том, что можно снова и снова применять алгоритм Штрассена к меньшим матрицам и с помощью его метода сокращать количество шагов на каждом этапе. В целом алгоритм Штрассена увеличил скорость умножения матриц с n 3 до n 2.81 мультипликативных шагов.

Следующий важный шаг в развитии идеи произошел в конце 1970-х, когда появился принципиально новый подход к решению этой задачи. Он подразумевает перевод матричного умножения в другую вычислительную задачу линейной алгебры с использованием объектов, называемых тензорами. Тензоры, используемые в этой задаче, представляют собой трехмерные массивы чисел, состоящие из множества различных частей, каждая из которых выглядит как небольшая задача на умножение матриц.

Умножение матриц и эта задача, связанная с тензорами, в определенном смысле эквивалентны друг другу, но для решения последней исследователи уже имели более быстрые процедуры. Таким образом, перед ними встала задача определить «обменный курс» между ними: Матрицы какого размера можно перемножить при тех же вычислительных затратах, которые требуются для решения тензорной задачи?

«Это очень распространенная в теоретической информатике концепция: преобразовывать задачи и проводить аналогию между ними, чтобы показать, что они одинаково простые или сложные», — сказал Алман.

В 1981 году Арнольд Шёнхаге использовал этот подход, чтобы доказать, что умножение матриц возможно выполнить за n 2.522 шагов. Позднее Штрассен назвал этот подход «лазерным методом» (laser method).

За последние несколько десятилетий каждое улучшение в процессе умножения матриц происходило за счет усовершенствования лазерного метода, поскольку исследователи находили все более эффективные способы трансформации задачи. В своем новом доказательстве Алман и Уильямс стирают различие между 2 задачами и показывают, что уменьшить число умножений возможно. «В целом Джош и Вирджиния нашли способ применить машинные вычисления в рамках лазерного метода и получили лучшие на настоящий момент результаты», — сказал Генри Кон из Microsoft Research.

Но, несмотря на все эти гонки и победы, становится ясно, что в случае с этим подходом действует закон убывающей доходности, или убывающей отдачи. Скорее всего, усовершенствование Алмана и Уильямс почти полностью исчерпало возможности лазерного метода, но так и не позволило достичь конечной теоретической цели.

«Маловероятно, что получится приблизиться ко второй степени, используя это семейство методов», — отметил Уманс.

Для этого потребуется открытие новых методов и стойкая вера в то, что это вообще возможно.
Уильямс вспоминает один из разговоров со Штрассеном об этом: «Я спросила его, считает ли он, что возможно получить вторую степень для матричного умножения, и он ответил: «Нет, нет, нет, никогда!».

Источник

Умножение матриц: примеры, алгоритм действий, свойства произведения

Произведение двух матриц

Произведение матриц (С= АВ) — операция только для согласованных матриц А и В, у которых число столбцов матрицы А равно числу строк матрицы В:

C ⏟ m × n = A ⏟ m × p × B ⏟ p × n

Вычислим произведения АВ=ВА:

Решение, используя правило умножения матриц:

А ⏟ 2 × 3 × В ⏟ 3 × 2 = 1 2 1 0 1 2 × 1 0 0 1 1 1 = 1 × 1 + 2 × 0 + 1 × 1 1 × 0 + 2 × 1 + 1 × 1 0 × 1 + 1 × 0 + 2 × 1 0 × 0 + 1 × 1 + 2 × 1 = = 2 3 2 3 ⏟ 2 × 2

В ⏟ 3 × 2 × А ⏟ 2 × 3 = 1 0 0 1 1 1 × 1 2 1 0 1 2 = 1 × 1 + 0 × 0 1 × 2 + 0 × 1 1 × 1 + 0 × 2 0 × 1 + 1 × 0 0 × 2 + 1 × 1 0 × 1 + 1 × 2 1 × 1 + 1 × 0 1 × 2 + 1 × 1 1 × 1 + 1 × 2 = 1 2 1 0 1 2 1 3 3 ⏟ 3 × 3

Свойства умножения матриц

Свойства умножения матриц:

Проверяем свойство №1: ( А В ) С = А ( В С ) :

Проверяем свойство №2: А ( В + С ) = А В + А С :

Произведение трех матриц

Произведение трех матриц А В С вычисляют 2-мя способами:

Перемножить матрицы 2-мя способами:

Алгоритм действий:

Используем формулу А В С = ( А В ) С :

Умножение матрицы на число

Произведение матрицы А на число k — это матрица В = А k того же размера, которая получена из исходной умножением на заданное число всех ее элементов:

Свойства умножения матрицы на число:

Найдем произведение матрицы А = 4 2 9 0 на 5.

5 А = 5 4 2 9 0 5 × 4 5 × 2 5 × 9 5 × 0 = 20 10 45 0

Умножение матрицы на вектор

Чтобы найти произведение матрицы и вектора, необходимо умножать по правилу «строка на столбец»:

А В = а 11 а 12 ⋯ а 1 n а 21 а 22 ⋯ а 2 n ⋯ ⋯ ⋯ ⋯ а m 1 а m 2 ⋯ а m n b 1 b 2 ⋯ b 1 n = a 11 × b 1 + a 12 × b 2 + ⋯ + a 1 n × b n a 21 × b 1 + a 22 × b 2 + ⋯ + a 2 n × b n ⋯ ⋯ ⋯ ⋯ a m 1 × b 1 + a m 2 × b 2 + ⋯ + a m n × b n = c 1 c 2 ⋯ c 1 m

А В = а а ⋯ а b b ⋯ b = a 1 × b 1 a 1 × b 2 ⋯ a 1 × b n a 2 × b 1 a 2 × b 2 ⋯ a 2 × b n ⋯ ⋯ ⋯ ⋯ a n × b 1 a n × b 2 ⋯ a n × b n = c 11 c 12 ⋯ c 1 n c 21 c 22 ⋯ c 2 n ⋯ ⋯ ⋯ ⋯ c n 1 c n 2 ⋯ c n n

Найдем произведение матрицы А и вектора-столбца В :

Найдем произведение матрицы А и вектора-строку В :

Источник

Умножение матриц

Итак, в предыдущем уроке мы разобрали правила сложения и вычитания матриц. Это настолько простые операции, что большинство студентов понимают их буквально с ходу.

Однако вы рано радуетесь. Халява закончилась — переходим к умножению. Сразу предупрежу: умножить две матрицы — это вовсе не перемножить числа, стоящие в клеточках с одинаковыми координатами, как бы вы могли подумать. Тут всё намного веселее. И начать придётся с предварительных определений.

Согласованные матрицы

Ещё раз: количество столбцов в первой матрице равно количеству строк во второй! Отсюда получаем сразу два вывода:

Определение умножения

По-моему, тут всё очевидно. Дальше можно не читать. [на самом деле нет]

У тех, кто впервые видит это определение, сразу возникает два вопроса:

Что ж, обо всём по порядку. Начнём с первого вопроса. Что означают все эти индексы? И как не ошибиться при работе с реальными матрицами?

Данный процесс легко понять по картинке:

Схема перемножения двух матриц

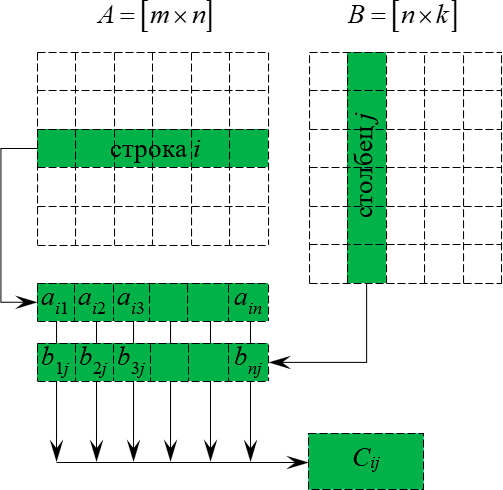
На самом деле мы уже встречались с перемножением матриц в школьной программе, только в сильно урезанном виде. Пусть даны вектора:

Тогда их скалярным произведением будет именно сумма попарных произведений:

Сегодня ничего не поменялось. Просто теперь этих векторов-строк и столбцов стало больше.

Но хватит теории! Давайте посмотрим на реальные примеры. И начнём с самого простого случая — квадратных матриц.

Умножение квадратных матриц

Задача 2. Выполните умножение:

Решение. Опять согласованные матрицы, поэтому выполняем действия:\[\]

Как видим, получилась матрица, заполненная нулями

Из приведённых примеров очевидно, что умножение матриц — не такая уж и сложная операция. По крайней мере для квадратных матриц размера 2 на 2.

В процессе вычислений мы составили промежуточную матрицу, где прямо расписали, какие числа входят в ту или иную ячейку. Именно так и следует делать при решении настоящих задач.

Основные свойства матричного произведения

В двух словах. Умножение матриц:

А теперь — всё то же самое, но более подробно.

Умножение матриц во многом напоминает классическое умножение чисел. Но есть отличия, важнейшее из которых состоит в том, что умножение матриц, вообще говоря, некоммутативно.

Рассмотрим ещё раз матрицы из задачи 1. Прямое их произведение мы уже знаем:

Но если поменять матрицы местами, то получим совсем другой результат:

Тем не менее, умножение матриц ассоциативно:

\[\left( A\cdot B \right)\cdot C=A\cdot \left( B\cdot C \right)\]

Следовательно, когда вам надо перемножить сразу несколько матриц подряд, совсем необязательно делать это напролом: вполне возможно, что некоторые рядом стоящие матрицы при перемножении дают интересный результат. Например, нулевую матрицу, как в Задаче 2, рассмотренной выше.

Такая матрица всегда выглядит одинаково: на главной диагонали её стоят единицы, а во всех остальных клетках — нули.

Идём далее. Помимо ассоциативности умножение матриц ещё и дистрибутивно:

Другими словами, если нужно умножить одну матрицу на сумму двух других, то можно умножить её на каждую из этих «двух других», а затем результаты сложить. На практике обычно приходится выполнять обратную операцию: замечаем одинаковую матрицу, выносим её за скобку, выполняем сложение и тем самым упрощаем себе жизнь.:)

Заметьте: для описания дистрибутивности нам пришлось прописать две формулы: где сумма стоит во втором множителе и где сумма стоит в первом. Это происходит как раз из-за того, что умножение матриц некоммутативно (и вообще, в некоммутативной алгебре куча всяких приколов, которые при работе с обычными числами даже не приходят в голову). И если, допустим, вам на экзамене нужно будет расписать это свойство, то обязательно пишите обе формулы, иначе препод может немного разозлиться.

Ладно, всё это были сказки о квадратных матрицах. А что насчёт прямоугольных?

Случай прямоугольных матриц

А ничего — всё то же самое, что и с квадратными.

Сейчас рассмотрим одно из лучших тренировочных заданий для тех, кто только начинает работать с матрицами. В нём нужно не просто перемножить какие-то две таблички, а сначала определить: допустимо ли такое умножение?

Рекомендую после прочтения задания не смотреть в решение, а сначала попробовать выполнить его самостоятельно. И затем сравнить с ответами.

Задача 4. Найдите все возможные попарные произведения матриц:

Решение. Для начала запишем размеры матриц:

\[A=\left[ 2\times 4 \right];\ B=\left[ 4\times 2 \right];\ C=\left[ 2\times 2 \right]\]

Промежуточные шаги предлагаю выполнить читателю самостоятельно. Замечу лишь, что размер результирующей матрицы лучше определять заранее, ещё до каких-либо вычислений:

\[A \cdot B=\left[ 2\times 4 \right]\cdot \left[ 4\times 2 \right]=\left[ 2\times 2 \right]\]

Другими словами, мы просто убираем «транзитные» коэффициенты, которые обеспечивали согласованность матриц.

\[B \cdot A=\left[ 4\times 2 \right]\cdot \left[ 2\times 4 \right]=\left[ 4\times 4 \right]\]

\[B\cdot C=\left[ \begin<*<35>>1 & 0 \\ 0 & 2 \\ 3 & 0 \\ 0 & 4 \\\end \right]\]

Вообще, очень рекомендую выполнить это задание самостоятельно. И ещё одно аналогичное задание, которое есть в домашней работе. Эти простые на первый взгляд размышления помогут вам отработать все ключевые этапы умножения матриц.

Но на этом история не заканчивается. Переходим к частным случаям умножения.:)

Вектор-строки и вектор-столбцы

Одной из самых распространённых матричных операций является умножение на матрицу, в которой одна строка или один столбец.

Задача 6. Выполните умножение:

На самом деле мне было в лом считать все эти три числа — посчитайте сами. А я просто запишу ответ.:)

Как видите, при умножении вектор-строки и вектор-столбца на квадратную матрицу на выходе мы всегда получаем строку или столбец того же размера. Этот факт имеет множество приложений — от решения линейных уравнений до всевозможных преобразований координат (которые в итоге тоже сводятся к системам уравнений, но давайте не будем о грустном).

Думаю, здесь всё было очевидно. Переходим к заключительной части сегодняшнего урока.

Возведение матрицы в степень

Среди всех операций умножения отдельного внимания заслуживает возведение в степень — это когда мы несколько раз умножаем один и тот же объект на самого себя. Матрицы — не исключение, их тоже можно возводить в различные степени.

Такие произведения всегда согласованы:

\[A\cdot A=\left[ n\times n \right]\cdot \left[ n\times n \right]=\left[ n\times n \right]\]

И обозначаются точно так же, как и обычные степени:

На первый взгляд, всё просто. Посмотрим, как это выглядит на практике:

Задача 7. Возведите матрицу в указанную степень:

Решение. Ну ОК, давайте возводить. Сначала возведём в квадрат:

\[\begin & <<\left[ \begin1 & 1 \\ 0 & 1 \\\end \right]>^<2>>=\left[ \begin 1 & 1 \\ 0 & 1 \\\end \right]\cdot \left[ \begin 1 & 1 \\ 0 & 1 \\\end \right]= \\ & =\left[ \begin<*<35>> 1\cdot 1+1\cdot 0 & 1\cdot 1+1\cdot 1 \\ 0\cdot 1+1\cdot 0 & 0\cdot 1+1\cdot 1 \\\end \right]= \\ & =\left[ \begin<*<35>> 1 & 2 \\ 0 & 1 \\\end \right] \end\]

\[\begin & <<\left[ \begin1 & 1 \\ 0 & 1 \\\end \right]>^<3>>= <<\left[ \begin1 & 1 \\ 0 & 1 \\\end \right]>^<3>>\cdot \left[ \begin 1 & 1 \\ 0 & 1 \\\end \right]= \\ & =\left[ \begin<*<35>> 1 & 2 \\ 0 & 1 \\\end \right]\cdot \left[ \begin 1 & 1 \\ 0 & 1 \\\end \right]= \\ & =\left[ \begin<*<35>> 1 & 3 \\ 0 & 1 \\\end \right] \end\]

Задача 8. Возведите матрицу в указанную степень:

Решение. Вот только не надо сейчас плакать по поводу того, что «степень слишком большая», «мир не справедлив» и «преподы совсем берега потеряли». На самом деле всё легко:

\[\begin & <<\left[ \begin1 & 1 \\ 0 & 1 \\\end \right]>^<10>>= <<\left[ \begin1 & 1 \\ 0 & 1 \\\end \right]>^<3>>\cdot <<\left[ \begin1 & 1 \\ 0 & 1 \\\end \right]>^<3>>\cdot <<\left[ \begin1 & 1 \\ 0 & 1 \\\end \right]>^<3>>\cdot \left[ \begin 1 & 1 \\ 0 & 1 \\\end \right]= \\ & =\left( \left[ \begin 1 & 3 \\ 0 & 1 \\\end \right]\cdot \left[ \begin 1 & 3 \\ 0 & 1 \\\end \right] \right)\cdot \left( \left[ \begin 1 & 3 \\ 0 & 1 \\\end \right]\cdot \left[ \begin 1 & 1 \\ 0 & 1 \\\end \right] \right)= \\ & =\left[ \begin 1 & 6 \\ 0 & 1 \\\end \right]\cdot \left[ \begin 1 & 4 \\ 0 & 1 \\\end \right]= \\ & =\left[ \begin 1 & 10 \\ 0 & 1 \\\end \right] \end\]

Заметьте: во второй строчке мы использовали ассоциативность умножения. Собственно, мы использовали её и в предыдущем задании, но там это было неявно.

Как видите, ничего сложного в возведении матрицы в степень нет. Последний пример можно обобщить:

Этот факт легко доказать через математическую индукцию или прямым перемножением. Однако далеко не всегда при возведении в степень можно выловить подобные закономерности. Поэтому будьте внимательны: зачастую перемножить несколько матриц «напролом» оказывается проще и быстрее, нежели искать какие-то там закономерности.

Задача 9. Возведите матрицу в указанную степень:

Решение. Не будем искать закономерности. Работаем «напролом»:

\[ <<\left[ \begin0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\\end \right]>^<3>>= <<\left[ \begin0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\\end \right]>^<2>>\cdot \left[ \begin0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\\end \right]\]

Для начала возведём эту матрицу в квадрат:

\[\begin & <<\left[ \begin0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\\end \right]>^<2>>=\left[ \begin 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\\end \right]\cdot \left[ \begin 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\\end \right]= \\ & =\left[ \begin<*<35>> 2 & 1 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 2 \\\end \right] \end\]

Теперь возведём в куб:

\[\begin & <<\left[ \begin0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\\end \right]>^<3>>=\left[ \begin<*<35>> 2 & 1 & 1 \\ 1 & 2 & 1 \\ 1 & 1 & 2 \\\end \right]\cdot \left[ \begin 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\\end \right]= \\ & =\left[ \begin<*<35>> 2 & 3 & 3 \\ 3 & 2 & 3 \\ 3 & 3 & 2 \\\end \right] \end\]

Вот и всё. Задача решена.

Как видите, объём вычислений стал больше, но смысл от этого нисколько не поменялся.:)

На этом урок можно заканчивать. В следующий раз мы рассмотрим обратную операцию: по имеющемуся произведению будем искать исходные множители.

Как вы уже, наверное, догадались, речь пойдёт об обратной матрице и методах её нахождения.

Источник

Умножение матриц.

Умножение матриц – это одна из самых распространенных операций с матрицами. Матрица, которая получается после умножения, называется произведением матриц.

Произведением матрицы A_m×n на матрицу B_n×k будет матрица C_m×k такая, что элемент матрицы C, находящийся в i-ой строке и j-ом столбце, то есть элемент c_ij равен сумме произведений элементов i-ой строки матрицы A на соответствующие элементы j-ого столбца матрицы B.

Процесс умножения матриц возможен только в случае, когда число столбцов первой матрицы равно числу строк второй матрицы.

Пример:
Можно ли умножить матрицу 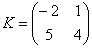на матрицу ?

m = n, значит, умножать данные матрицы можно.

Если же матрицы поменять местами, то, при таких матрицах, умножение уже не будет возможно.

m ≠ n, таким образом, выполнять умножение нельзя:

Довольно часто можно встретить задания с подвохом, когда ученику предлагается умножить матрицы, умножение которых заведомо невозможно.

Обратите внимание, что иногда можно умножать матрицы и так, и так. К примеру, для матриц, и возможно как умножение MN, так и умножение NM.

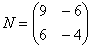
Операция умножения матриц.

Операция умножения матриц – это не очень сложное действие. Умножение матриц лучше понимать на конкретных примерах, т.к. только определение может сильно запутать.

Начнем с самого простого примера:

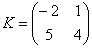
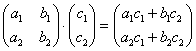
Необходимо умножить на . Первым делом приведем формулу для данного случая:

– здесь хорошо прослеживается закономерность.

Далее более сложный пример:

Умножить на .

Формула для этого случая: .

Умножение матриц и результат:

В результате получена т.н. нулевая матрица.

Очень важно помнить, что здесь не работает «правило перестановки мест слагаемых» так как почти всегда MN ≠ NM. Поэтому, производя операцию умножения матриц их ни в коем случае нельзя менять местами.

Теперь рассмотрим примеры умножения матриц третьего порядка:

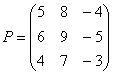
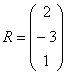
Умножить на .

Формула очень похожа на прошлые:

Решение матрицы: .

Умножение матрицы на число.

Умножение матрицы на число – это тоже самое умножение матриц, только вместо второй матрицы берется простое число. Как можно догадаться, такое умножение выполнять гораздо проще.

Пример умножения матрицы на число:

Тут все понятно – для того, чтобы умножить матрицу на число, необходимо каждый элемент матрицы последовательно умножить на указанное число. В данном случае – на 3.

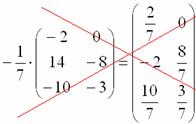
Еще один полезный пример:

– умножение матрицы на дробное число.

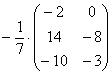
Первым делом покажем то, чего делать не надо:

При умножении матрицы на дробное число не нужно вносить дробь в матрицу, так как это в первую очередь только затрудняет дальнейшие действия с матрицей, во-вторых, затрудняет проверку решения преподавателем.

.

Что стоит сделать в данном случае – это внести минус в матрицу:

.

Если бы у вас был пример, когда все элементы матрицы делились бы на 7 без остатка, то тогда можно (и нужно!) было бы поделить.

В данном примере можно и нужно умножить все элементы матрицы на ½, т.к. каждый элемент матрицы делится на 2 без остатка.

Примечание: в теории высшей математики школьного понятия «деление» нет. Вместо фразы «это поделить на это» всегда можно сказать «это умножить на дробь». То есть, деление – это частный случай умножения.

Источник