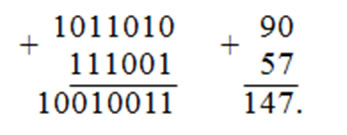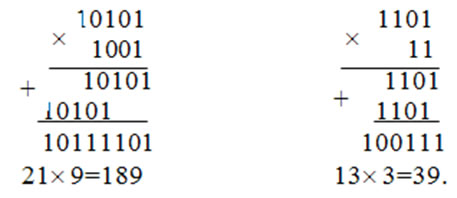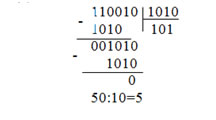Как умножаются двоичные числа
Двоичная система счисления
Содержание:
Вспомним материал по системам счисления. В нём говорилось, что наиболее удобной системой счисления для компьютерных систем является двоичная система. Дадим определение этой системе:
Двоичной системой счисления называется позиционная система счисления, у которой основанием является число 2.
Для записи любого числа в двоичной системе счисления используются всего лишь 2 цифры: 0 и 1.
Общая форма записи двоичных чисел
Для целых двоичных чисел можно записать:
Данная форма записи числа «подсказывает» правило перевода натуральных двоичных чисел в десятичную систему счисления: требуется вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа.
Правила сложения двоичных чисел
Основные правила сложения однобитовых чисел
Отсюда видно, что и, как и в десятичной системе счисления, числа, представленные в двоичной системе счисления, складывают поразрядно. Если разряд переполняется, единица переносится в следующий разряд.
Пример сложения двоичных чисел
Правила вычитания двоичных чисел
Но как быть с 0-1=? Вычитание двоичных чисел немного отличается от вычитания десятичных чисел. Для этого используется несколько способов.
Вычитание методом заимствования
Запишите двоичные числа друг под другом – меньшее число под большим. Если меньшее число имеет меньше цифр, выровняйте его по правому краю (так, как вы записываете десятичные числа при их вычитании).
Некоторые задачи на вычитание двоичных чисел ничем не отличаются от вычитания десятичных чисел. Запишите числа друг под другом и, начиная справа, найдите результат вычитания каждой пары чисел.
Вот несколько простых примеров:
Вычтите цифры в оставшихся столбцах. Теперь это легко сделать (работайте со столбцами, двигаясь, справа налево):
Вычитание методом дополнения
Запишите двоичные числа друг под другом так, как вы записываете десятичные числа при их вычитании. Этот метод используется компьютерами для вычитания двоичных чисел, так как он основан на более эффективном алгоритме.
Однако простому человеку, привыкшему вычитать десятичные числа, этот метод может показаться более сложным (если вы программист, обязательно познакомьтесь с этим методом вычитания двоичных чисел).
Если значность чисел разная, к числу с меньшей значностью слева припишите соответствующее количество 0.
В вычитаемом числе поменяйте цифры: каждую 1 поменяйте на 0, а каждый 0 на 1.
0111012 → 1000102.
К полученному вычитаемому прибавьте единицу.
1000102+ 12 = 1000112
Теперь вместо вычитания сложите два двоичных числа.
Проверьте ответ. Быстрый способ – откройте двоичный онлайн калькулятор и введите в него вашу задачу. Два других метода подразумевают проверку ответа вручную.
1) Переведем числа в двоичную систему счисления:
Допустим, что из числа 1011012 нужно вычесть 110112
2) Обозначим как A число 1011012 и как B число 110112.
3) Запишем числа A и B столбиком, одно под другим, начиная с младших разрядов (нумерация разрядов начинается с нуля).
Двоичный калькулятор онлайн
Данный калькулятор может производить следующие действия над двоичными числами:
Сложение двоичных чисел
Сложение двух двоичных чисел производится столбиком поразрядно. Начиная с младшего разряда (справа на лево), как и при сложении столбиком десятичных чисел. Но так как цифр всего две (0 и 1), их сложение происходит по следующим правилам:
Пример
Для примера сложим 1011 и 101:
| + | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | ||
| 1 | 0 | 0 | 0 | 0 |
Вычитание двоичных чисел
Вычитание двоичных чисел производится аналогично сложению – столбиком, но по следующим правилам:
Пример
Для примера вычтем из числа 1011 число 101:
| − | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | ||
| 1 | 1 | 0 |
Умножение двоичных чисел
Умножение двоичных чисел производится в столбик аналогично умножению в десятичной системе, но по следующим правилам:
Пример
Для примера перемножим числа 1011 и 101:
| × | 1 | 0 | 1 | 1 | |
| 1 | 0 | 1 | |||
| + | 1 | 0 | 1 | 1 | |
| 0 | 0 | 0 | 0 | ||
| 1 | 0 | 1 | 1 | ||
| 1 | 1 | 0 | 1 | 1 | 1 |
Деление двоичных чисел
Внешне деление двоичных чисел похоже на деление десятичных чисел, но тут есть свои нюансы: такое деление производится вычитанием делителя со сдвигом вправо, если остаток больше нуля. Чтобы понять этот процесс рассмотрим пример:
Двоичная арифметика

Всего получено оценок: 190.
Всего получено оценок: 190.
Операции сложения, вычитания, умножения и деления в двоичной системе – это двоичная арифметика. Некоторые примеры двоичной арифметики рассмотрены в данной статье.
Двоичная арифметика
Все арифметические действия, которые применимы к двоичным числам, выполняются аналогично как в десятичной системе. Удобнее всего двоичные числа складывать, вычитать, умножать и делить столбиком.
Числа записываются друг под другом с учетом разрядов. При необходимости производится перенос в старший разряд или заем из старшего разряда.
При сложении двоичных чисел следует помнить, что в числовом двоичном ряду после 1 идет 10. Это означает, что 1 + 1 = 10, а 11 + 1= 100.
Изучению двоичной системы много времени посвятил В. Лейбниц. По его просьбе была отчеканена медаль в честь двоичной системы, на которой отображались простейшие арифметические действия с двоичными числами.
Сложение
Вычисление суммы двоичных чисел производится следующим образом: числа записываются в столбик. Затем производится поразрядное суммирование цифр, начиная с младшего разряда, как в десятичной системе. Если сумма цифр текущего разряда превышает его размер, то происходит перенос единицы в старший разряд.
Правила сложения двоичных чисел:
Например, сумма двоичных чисел 1000111 + 110011 = 1111010
Арифметические операции в двоичной системе
Арифметические действия в двоичной системе производится по тем же правилам что и в десятичной системе счисления. Однако так как в двоичной системе счисления используются только две цифры 0 и 1, то арифметические действия выполняются проще, чем десятичной системе.
Сложение двоичных чисел.
Сложение выполняется поразрядно столбиком, начиная с младшего разряда и используя таблицы двоичного сложения:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10.
При сложении необходимо помнить, что 1+1 дают нуль в данном разряде и единицу переноса в старший.
Пример 3.5. Сложить два числа:
Вычитание двоичных чисел.
Вычитание выполняется поразрядно столбиком, начиная с младшего разряда и используя таблицы двоичного вычитания:
0 – 0 = 0
1 – 0 = 1
1 – 1 = 0
10 – 1 = 1.
Пример 3.6. Найти разность двух чисел:
Т.е. при вычитании двоичных чисел в случае необходимости занимается 1 из старшего разряда, которая равна двум единицам младшего разряда.
Умножение двоичных чисел.
Как видно из приведенных примеров, операция умножения может быть представлена как операции сдвига и суммирования.
Деление двоичных чисел.
Деление в двоичной системе производится вычитанием делителя со сдвигом вправо, если остаток больше нуля.
Пример 3.8. Найти частное двух чисел если:
1. Делимое больше делителя:
2. Делимое меньше делителя:
Как видно из приведенных примеров, операция деления может быть представлена как операции сравнения, сдвига и суммирования.
Вернуться в оглавление:Алгоритмические языки
Когда используется двоичная система счисления, числа выражаются посредством использования нуля и единицы. Компьютеры в своей работе используют двоичные числа. Они могут быть целыми или дробными.
С их помощью могут быть выражены все буквы алфавита. Однако для человека более привычна десятичная система.
В статье будет рассказано, как делать расчёты с использованием бинарных чисел и как преобразовывать их в более привычную десятичную систему и в противоположном направлении.
Сложение, вычитание и умножение двоичных чисел
Действия с бинарными числами, состоящими из нулей и единиц, выполняются по правилам арифметики, которые аналогичны используемым в десятичной системе.
Это верно для всех основных операций, используемых в арифметике — сложения, вычитания, умножения, деления.
Для вычисления можно проводить расчёты самостоятельно или использовать онлайн калькулятор.
Сложение
При сложении двух двоичных чисел удобно их расположить в столбик друг над другом. Аналогичным образом можно проводить вычисления с дробями.
При этом вычисления производятся так же, как обычно, за исключением правила, по которому делается перенос в старший разряд. Если, когда складывают цифры, на определённом месте переноса будет получено два или три, то единица будет перенесена в старший разряд.
После завершения вычисления всех значащих цифр будет получена сумма двух бинарных чисел.
Вычитание
Это можно делать обычным образом, однако на практике распространён ещё один вариант.
При вычитании двоичных чисел обычно используется дополнение для вычитаемого. Это форма для выражения отрицательного числа. Оно получается путём замены всех единиц — на нули, а нулей — на единицы.
Полученное таким образом вычитаемое требуется обычным образом сложить с уменьшаемым. После этого старшую единицу отбрасывают.
Результат — разность, полученная при вычислении в двоичном коде.
Умножение
Умножать в информатике можно, пользуясь обычными правилами для вычисления в столбик.
Перевод десятичного числа в двоичное
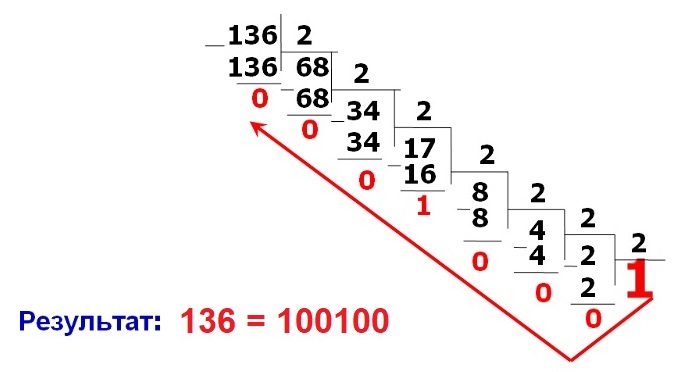
Для того чтобы представить обычное число в бинарном виде, нужно воспользоваться операцией деления на два. При первом вычислении будут получены частное и остаток.
Затем частное ещё раз делят на два. Снова записывают результаты. Продолжают повторять до получения единицы.
Первый остаток будет младшим битом числа, второй — следующим. Таким образом все остатки выписывают справа налево и получают число в двоичной системе, равное по своему значению первоначальному десятичному.
Возможно составить таблицу, которая покажет все двоичные разряды этого числа.
Примеры перевода чисел
Далее будет рассмотрено преобразование десятичного числа 23 в двоичную форму.
Запишем результаты деления на два:
23 делим на 2 — при этом частное равно 11, остаток — 1;
11 пополам — в результате частное будет 5, в остатке — 1;
5 снова делим — частное 2, остаток 1;
2 на 2 — здесь получится 1, остатком будет 0;
последний остаток равен 1.
Итак, было получено 10111, представленное в двоичном виде. Теперь будет сделан его перевод в десятичный вид. Для этого нужно использовать следующую формулу:
1 * 16 + 0 * 8 + 1 * 4 + 1 * 2 + 1 * 1 = 16 + 4 + 2 + 1 = 23.
Таким образом проверка показала, что было получено число с основанием 2, которое имеет то же самое значение.