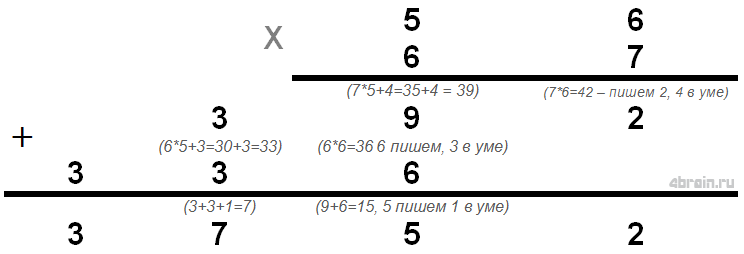Как умножают в америке
Как не запутаться в американской системе мер
Всем привет! Решил написать для вас этот пост про Американскую систему мер и как в ней ориентироваться. На самом деле всё намного проще, чем кажется =) Для полного погружения в атмосферу я буду использовать американскую систему чисел в посте. Поехали!
Наша первая остановка — магазин, деньги и школа.
Знак доллара пишется спереди числа, в то время как знак цента — после. При произношении оба знака говорятся в конце.
У монеток центов есть свои имена! И в повседневной речи используются именно они, никто не говорит «five cents, ten cents».
Penny (пенни) — 1с
Nickel (никель) — 5с
Dime (дайм) — 10с
Quarter (четвертак) — 25с
В магазине в конце цены всегда два знака отделены точкой для значения центов, даже если сумма «кругленькая». Например:
Часто ноль перед десятичной дробью просто не пишется. Десятичные дроби отделяются точкой, а не запятой. Запятой отделяются тысячи.
Большие числа, как, например, 2,956 чаще всего читаются не «two thousand nine hundred and fifty-six», как думают многие, а вот так: «twenty-nine fifty-six». Оба произношения допустимы.
> 256 — two fifty-six
> 1,900 — nineteen hundred
> 5,789 — fifty-seven eighty-nine
Формат даты также отличается от нашего: сначала пишется месяц, потом день, потом год. Если число однозначное, ноль перед ним не пишется. Дни недели пишутся с большой буквы. Сейчас, например, Wednesday, 8/13/2014
Касаемо десятичных дробей… В американской системе счета есть такое понятие, как significant figures. Я, проходя обучение в американской школе, так и не понял, что это за херня и нахера она вообще нужна, но суть, насколько мне известно, состоит в следующем:
Задание: решите пример
Зачем в конце эти нули? Да хер его знает!
Честно говоря, я не понимаю, зачем это надо, ведь опускать ноли было бы проще… Часто даже простые числа типа 3.50 имеют лишний ноль в конце. Ну да ладно, вернемся к нашим баранам.
Далее — повседневные величины:
Чтобы перевести текущую скорость из миль в час в км/ч, нужно просто умножить скорость на 1.6
> 1 миля = 1.60 км
Кстати, для определения расхода топлива автомобилем американцы используют не такую величину, как мы — сколько литров топлива машина сожрет на 100 километров пути — а наоборот: сколько миль автомобиль проедет на 1 галлоне топлива.
Чтобы узнать приблизительный рост человека, нужно его рост в футах разделить на три.
> 1 фут = .30 м
А маленькие измерения линейкой умножаются на 2.5 для перевода из дюймов в сантиметры.
> 1 дюйм = 2.50 см
Вес человека в фунтах будет примерно уменьшен в два раза при пересчете на килограммы.
> 1 фунт = .45 кг
Для шедевров кулинарных искусств не забудьте унции умножить на 30 — получите граммы.
> 1 унция = 30 гр
Касаемо кулинарии, вот вам еще:
> В одном фунте 16 унций
> 1 галлон = 3.80 литров
> 1 пинта (используется для пива) = .50 литров
> 1 жидкая унция (насколько я знаю, используется редко) = .03 литра
А теперь самое интересное: ёбнутые величины, моя любимая часть американской системы мер!
Градусы легче не переводить, т.к. это долго и муторно
> (°C x 9 / 5)+32=°F
а просто запомнить некоторые значения:
И напоследок вот вам сокращения измерений (ну, километр — км. и так далее)
Способы умножения
Все знают, как умножать в столбик, немного меньше людей знают об умножении линиями, но есть и другие интересные способы.
Умножение чисел — это очень простая операция, фактически, то же самое, что и суммирование. Конечно, пока сами числа не большие.
2х3=2+2+2 (три раза по два) или 24х6=24+24+24+24+24+24 (шесть раз по 24)
То есть, знать таблицу умножения вовсе не обязательно? Да, но с ней удобнее. Например, в случае умножения чисел 235х4596, число 4596 придется сложить 235 раз! Или наоборот, 235 сложить 4596 раз…
Слово «сложить» употреблено не зря. Вот простой способ в этом убедиться. Нужно взять листок бумаги сложить его 5 раз в одном направлении, а потом 3 раза в другом. Получится действие 5х3. Считаем получившиеся от сгибания прямоугольники — их 15. Это то же самое, если бы мы взяли 3 полоски ткани (или чего угодно) длинной 5 и сложили вместе.
Как ни крути, а получается — 15!
Необычные способы умножения
В школе нас учат использовать два инструмента: таблицу Пифагора (считается что таблицу умножения придумал именно этот греческий математик) и умножению «в столбик». Это действительно самые эффективные инструменты? Кроме них есть еще несколько интересных способов умножать числа. Может, какой-то из них будет проще и учить таблицу не придется?
По-крестьянски
Использовался для определения площади земельного участка. Например, имеем поле длинной 6 и шириной 5.
Чтобы узнать, сколько будет 6х5 делаем следующее: левое число делим на 2, а правое умножаем на 2, пока от левого числа не останется единица.
2/2= 1 | 10*2=20
4х5=20, все правильно, так же как и 1х20=20
Что происходит при таком способе? Мы разделяем прямоугольник пополам, пока его ширина не станет равняться единице. Делить на два не сложно.
Вот только что будет, если одна из сторон не будет делиться на 2? Будет долгий и не такой уж простой процесс.
6/2=3 | 2*2=4 → 12
3/2=1,5 | 4*2=8 → 12
Если в левой части четное число — эту строку не считаем, если значение меньше единицы — тоже отбрасываем, остается вторая и третья строка, а это 8+4=12. А если представить, что умножит нужно 173 на 735? Нет, такой способ умножения не самый легкий и простой.
Можно делить/умножать и на 3, но тогда нужно знать таблицу умножения «на три», тогда уж и 5 и 7 и… Да, удобнее выучить ее всю. Также, если будет необходимо перемножить большие числа, процесс будет очень длинным.
Восточный способ
То ли китайский, то ли японский способ умножения, при помощи линий, он же «графический». Его суть состоит в том, что цифры первого числа изображаются в виде параллельных линий, а второго — перпендикулярных им. Количество пересечений и является результатом умножения. То есть, здесь знать таблицу умножения не нужно, достаточно уметь суммировать. Например, так:
2 х 3 и даже 15 х 12
Японский или китайский метод, суть не меняется
Как работает умножение с помощью линий?
Первое число (фиолетовым цветом на картинке) рисуется так: Снизу вверх, слева на право, сначала тысячи, потом сотни, десятки, единицы. Второе число (голубым цветом на картинке) рисуется наоборот: сверху-вниз.
В первом примере все просто 2 и 3. Две линии пересекают 3 другие, получается 6 точек. Во втором, сначала рисуем 15 — единицу (один десяток), потом пять линий изображающих 5 (пять единиц). Потом (12) перпендикулярно ей вторую единицу и 2 линии.
Далее нужно посчитать пересечения, но уже в обратном направлении. Начинать справа. В примере это 10, 7 и 1. Результат складывается в столбик:
Если сравнить с традиционным «столбиком», сперва может показаться, что японско-китайский метод проще…
А что делать, если нужно умножить 10 на 12? Как изобразить «ноль» линией? Никак, он участия не принимает, можно нарисовать его пунктиром и пересечение не считать, все просто…
Но вот уже случае 853х951 рисовать и считать точки придется очень много. Старый-добрый столбик опять окажется удобнее. Каждый сам может попробовать перемножить 9878 и 8794 «японским методом» и засечь необходимое время.
Японский метод с нулем
Эта методика не универсальна, совсем не подходит, когда числа достаточно большие, зато ее очень просто объяснить маленьким детям, которые еще не знают таблицу умножения.
Жалюзи
Встречается еще и название «решетки» и индийский метод умножения. Поверить в индийское происхождение проще всего, если вспомнить, кто вообще придумывал эту вашу математику в древности. Итак, чтобы умножить два числа, нужно построить матрицу (если угодно — таблицу, мы же пытаемся быть проще).
Так как в каждом числе по 2 цифры, таблица будет 2х2. Каждую ячейку нежно перечеркнуть по диагонали. Далее записываем слева-на-право, и сверху-вниз цифры 4, 5, 8, 2 напротив каждой ячейки. Начинаем умножать цифры находящиеся напротив друг-друга. 4 на 8, 5 на 8, 4 на 2 и 5 на 2.
Ну вот опять нужна таблица умножения, иначе придется долго складывать числа.
Результаты записываются в ячейки хитрым способом, десятки над диагональю, а единицы — под ней. Но, если значение меньше 10 (то есть это одна, а не две цифры), то вместо десятки верху пишется «ноль», как при умножении 4х5. Но можно оставить поле пустым.
Теперь, чтобы узнать результат, нужно посчитать сумму в каждой диагонали, как показано на картинке. Сверху-вниз:
0+2+4=6
8+1=9
В результате получаем 3690.
Тоже достаточно просто, только с небольшими значениями, для умножения трехзначных чисел придется рисовать таблицу размером 3х3=9 ячеек.
Как умножать в столбик
Вот мы и добрались к самому традиционному методу. Так нас учат в школе умножать большие числа. Как же это работает и проще ли всех экзотически способов? Записываем два числа одно под другим 23х12:
1 2
Умножать начинаем «с конца». Берем последнюю цифру последнего числа, это 2. Умножаем на 3, получаем 6 и на 2, получаем 4. так и записываем их с конца 46. Повторяем то же самое со второй цифрой — 1.
Умножаем 1 на 3 и на 2. Записываем ниже 23. Только сместив на одну позицию влево. Так чтобы под цифрой 6 было пусто, а 2 оказалось под 4.
Все что осталось сделать, это сложить все цифры сверху вниз. 6+0, 4+3, 0+2. Если в какой то паре получается больше 9, то остаток переносится вправо. Так 4+3=7, но если бы мы сложили 5+6=11, то записали бы 1 и в правую колонку добавили бы еще 1.
Вы наверняка знаете как это все делается и делали сами. Но теперь, зная все остальные способы умножения можете оценить проще ли умножение в столбик всех остальных методов.
Какой метод умножения лучше?
Если перепробовать все способы умножения чисел, становится очевидно, что все представленные альтернативные методы умножения — это все варианты знакомого «столбика». Также операции разбиваются на более мелкие: сначала умножение, потом — суммирование.
Только в так называемом китайском/японском способе умножение как таковое не используется (вместо него пересечение линий) и в этом варианте действительно можно обойтись без таблицы умножения, но придется много рисовать, что повышает вероятность совершить ошибку при пересчете точек пересечения.
Есть мнение, что популярность умножения в столбик вызвана именно компактностью записи. Так на умножение требуется меньше бумаги, меньше чернил (да, чернила раньше использовались и тоже стоили денег) и, соответственно, времени.
Знать нетрадиционные методики интересно и даже полезно, но школьная таблица умножения, все же быстрее, а если вы знаете как умножать в столбик — это удобнее, чем любой другой способ. Если, конечно, не считать калькулятор.
Без калькулятора: умножаем большие числа в уме
В эру цифровых технологий у нас пропала необходимость запоминать телефоны и адреса, считать в голове. Даже ориентироваться на местности нам помогают гаджеты. Устный счет последний раз мы применяем в школе, а зря. Помимо удобства (ведь вы можете сами быстро все посчитать, не доставая смартфон), умение быстро умножать и делить здорово тренирует мозг. А если мозг не тренировать, он ленится, что приводит к ухудшению всех его функций и нашей продуктивности. Еще до времен повсеместного распространения вычислительных машин люди изобрели несколько лайфхаков устного счета. Рассмотрим их подробнее.
Гаусс — не только распределение
Еще когда будущий «король математиков» и автор закона, названного его именем, Карл Фридрих Гаусс отличался уникальными навыками. По легенде, примерно в возрасте 3 лет он заметил, что платежные ведомости его отца рассчитаны неправильно. После проверки оказалось, что мальчик был прав. В дальнейшем он продемонстрировал феноменальные математические способности. И некоторые лайфхаки устного счета называют тоже его именем.
Достаточно одной таблицы
Чтобы научиться перемножать любые числа, нам необходимо помнить таблицу умножения. Хитрость заключается в том, что любое большое число можно разложить на маленькие — те, что представлены в этой таблице. Суть умножения двух чисел заключается в многократном повторении одного из них. Например, 7 умножить на 3 — означает, что число 7 надо повторить 3 раза: 7+7+7 = 7*3 = 21.
Если перед нами стоит задача умножить однозначное число на многозначное, то достаточно разложить больше на маленькие по разрядам, т.е. сначала сотни, потом десятки, потом единицы. И по очереди их умножить на заданное число. Далее останется сложить эти произведения. Например, 254*7 = 200*7 + 50*7 + 4*7 = 1400 + 350 + 28 = 1778. Как мы видим, каждый разряд представляет собой однозначное число с определенным количеством нулей. Таким образом, нам нужно лишь помнить таблицу умножения, чтобы легко справиться с этой задачей.
Этот же способ применим для умножения двух двузначных чисел — их нужно так же разбить на однозначные и выполнить операцию последовательно. Допустим, наша задача умножить 67 на 43. 43 — это 40 + 3. А значит, 67 нужно умножить сначала на 40, затем на 3, и сложить эти произведения. Далее раскладываем 67 и производим ту же операцию. Получаем: 67*40 + 67*3 = 60*40 + 7*40 + 60*3 + 7*3 = 2400 + 280 + 180 + 21 = 2881.
Одиннадцать друзей умножения
Самый простой и интересный способ умножения двузначного числа — с использованием числа 11. Нужно всего лишь сложить между собой цифры, из которых состоит двузначное число. А по бокам поставить те же самые исходные 2 числа, которые мы складывали. Что получится, если 35 умножить на 11? Складываем 3 + 5 = 8, а по бокам ставим 3 и 5 — 385. Проверяем на калькуляторе. Но что делать, если сумма двух этих чисел больше 10? Куда что ставить? Нужно сделать все ровно так же, только при помощи наложения. Посмотрим на примере 83*11: 8 + 3 = 11. Посередине у нас стоит 11, справа 3, а к первому месту прибавляется 8, итого: 8 + 1 = 9 — это первое число. Далее у нас стояла единица, последней тройка. Собираем: 913. Проверяем. Вуаля!
Лайфхаки не тренировка
Конечно, само слово «лайфхак» подразумевает, что мы используем определенный прием, чтобы меньше напрягать мозг. При таком счете мозг тоже тренируется — ведь нам надо удерживать всю раскладку в голове, да еще и складывать эти элементы. Чтобы быстро выучить эти методики, а также дополнительно поддерживать функции мозга в тонусе, нам нужны полноценные тренировки. Они позволят освоить еще больше лайфхаков, быстро адаптироваться в незнакомых ситуациях и не теряться при виде больших данных.
Викиум разработал более 75 специальных — когнитивных тренажеров. Они развивают базовые (когнитивные) функции мозга комплексно, по запатентованной технологии. Программа составляет вам персональный план тренировок, следит за прогрессом, постепенно повышает нагрузку. Сами тренажеры выглядят как игровые задания с понятным интерфейсом — на них могут заниматься даже дети от 7 лет. В результате регулярных тренировок существенно увеличивается работоспособность мозга и ваша общая продуктивность. Занимайтесь каждый день всего по 10 минут и будьте в тонусе!
Китайское или японское умножение

В России мы привыкли умножать числа традиционным способом, которому нас учили в школе, записывая числа-множители столбиком (подробнее про наше умножение ). Однако в азиатских странах, таких как Япония и Китай принято считать иначе. Для созерцательного восточного менталитета важна непременная визуализация. Даже общепризнанные в мире арабские цифры китайцы и японцы записывают иероглифами. Именно с особенностью азиатской графической системы связан японский и китайский способ умножения чисел.
Это видео показывает, как умножать по-японски и по-китайски:
Многим покажется, что такой способ японского или китайского умножения слишком сложен и запутан, но это только на первый взгляд. Именно визуализация, то есть изображение всех точек пересечения прямых (множителей) на одной плоскости, дает нам зрительную поддержку, тогда как традиционный способ умножения подразумевает большое количество арифметических действий только в уме. Китайское или японское умножение помогает не только быстро и эффективно умножать двухзначные и трехзначные числа друг на друга без калькулятора, но и развивает эрудицию. Согласитесь, не каждый сможет похвастаться тем, что на практике владеет древнейшим китайским методом умножения (*), который актуален и прекрасно работает и в современном мире.
*) Японская или китайская таблица умножения? Археологами в Японии была найдена деревянная табличка с фрагментом таблицы умножения, которая предположительно была изготовлена в VIII веке. Учёные полагают, что подобные таблицы использовались японскими императорскими чиновниками, которым было необходимо осваивать разные науки, в том числе и арифметику.
Обнаруженная табличка — самая древняя из всех найденных в Японии ранее. Интересно, что иероглифы, которыми записаны цифры, по стилю графического начертания очень похожи на те, которые использовались как официальное письмо во времена китайской династии Тан VII-X века. Исходя из этого, ученые предположили, что таблица была скопирована из китайского учебника арифметики того времени, то есть вся японская таблица умножения была заимствована из Китая.
Именно к своим соседям в Китай ездили высокопоставленные японцы каждый год, чтобы перенять у них разные науки, такие как арифметику. Древняя китайская таблица умножения была не из простых, так как включала в себя умножение двузначных чисел друг на друга. Вряд ли все японские чиновники могли выучить такую таблицу наизусть, поэтому и носили с собой на работу что-то типа шпаргалок, фрагмент одной из которых и представляет собой найденная археологами в Японии табличка.
Итак, японская таблица умножения была заимствована у китайцев, которые, согласно некоторым гипотезам, и были одними из создателей первой арифметической системы, о чем свидетельствуют археологические находки, содержащие фрагменты таблицы умножения, возраст которых ученые оценили в 2700-3000 лет.
Урок 3. Традиционное умножение в уме

В данном уроке рассмотрены наиболее популярные приемы умножения двузначных чисел.
Первый способ – раскладка на десятки и единицы
Самым простым для понимания способом умножения двузначных чисел является тот, которому нас научили в школе. Он заключается в разбиении обоих множителей на десятки и единицы с последующим перемножением получившихся четырех чисел. Этот метод достаточно прост, но требует умения удерживать в памяти одновременно до трех чисел и при этом параллельно производить арифметические действия.
Проще такие примеры решаются в 3 действия. Сначала умножаются десятки друг на друга. Потом складываются 2 произведения единиц на десятки. Затем прибавляется произведение единиц. Схематично это можно описать так:
Для максимально быстрого эффекта потребуется хорошее знание таблицы умножения чисел до 10, умение складывать числа (до трехзначных), а также способность быстро переключать внимание с одного действия на другое, держа предыдущий результат в уме. Последний навык удобно тренировать путем визуализации совершаемых арифметических операций, когда вы должны представлять себе картинку вашего решения, а также промежуточные результаты.
Вывод. Не трудно убедиться в том, что этот способ не является самым эффективным, то есть позволяющим при наименьших действиях получить правильный результат. Следует принять во внимание другие способы.
Второй способ – арифметические подгонки
Приведение примера к удобному виду является достаточно распространенным способом счета в уме. Подгонять пример удобно, когда вам нужно быстро найти примерный или точный ответ. Желание подгонять примеры под определенные математические закономерности часто воспитывается на математических кафедрах в университетах или в школах в классах с математическим уклоном. Людей учат находить простые и удобные алгоритмы решения различных задач. Вот некоторые примеры подгонки:
Пример 49*49 может решаться так: (49*100)/2-49. Сначала считается 49 на сто – 4900. Затем 4900 делится на 2, что равняется 2450, затем вычитается 49. Итого 2401.
Произведение 56*92 решается так: 56*100-56*2*2*2. Получается: 56*2= 112*2=224*2=448. Из 5600 вычитаем 448, получаем 5152.
Этот способ может оказаться эффективнее предыдущего только в случае, если вы владеете устным счетом на базе перемножения двузначных чисел на однозначные и можете держать в уме одновременно несколько результатов. К тому же приходится тратить время на поиск алгоритма решения, а также уходит много внимания за правильным соблюдением этого алгоритма.
Вывод. Способ, когда вы стараетесь умножить 2 числа, раскладывая их на более простые арифметические процедуры, отлично тренирует ваши мозги, но связан с большими мысленными затратами, а риск получить неправильный результат выше, чем при первом методе.
56*67 – посчитаем в столбик.
Наверное, счет столбиком содержит максимальное количество действий и требует постоянно держать в уме вспомогательные числа. Но его можно упростить. Во втором уроке рассказывалось, что важно уметь быстро умножать однозначные числа на двузначные. Если вы уже умеете это делать на автомате, то счет в столбик в уме для вас будет не таким уж и трудным. Алгоритм таков
Первое действие: 56*7 = 350+42=392 – запомните и не забывайте до третьего действия.
Второе действие: 56*6=300+36=336 (ну или 392-56)
Третье действие: 336*10+392=3360+392=3 752 – тут посложнее, но вы можете начинать называть первое число, в котором уверены – «три тысячи…», а пока говорите, складывайте 360 и 392.
Вывод: счет в столбик напрямую сложен, но вы можете, при наличии навыка быстрого умножения двузначных чисел на однозначные, его упросить. Добавьте в свой арсенал и этот метод. В упрощенном виде счет в столбик является некоторой модификацией первого метода. Что лучше – вопрос на любителя.
Как можно заметить, ни один из описанных выше способов не позволяет считать в уме достаточно быстро и точно все примеры умножения двузначных чисел. Нужно понимать, что использование традиционных способов умножения для счета в уме не всегда является рациональным, то есть позволяющим при наименьших усилиях достигать максимального результата.