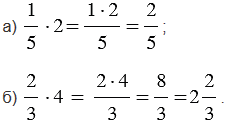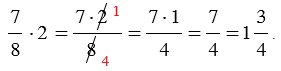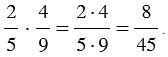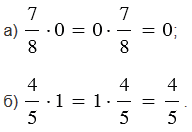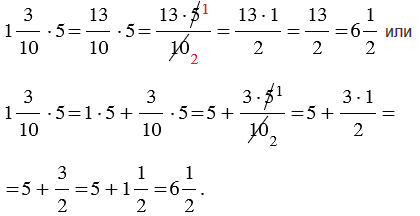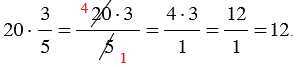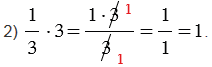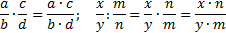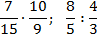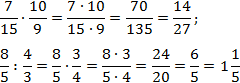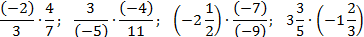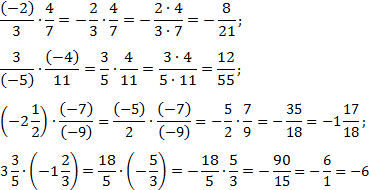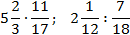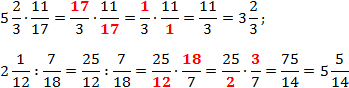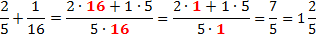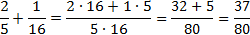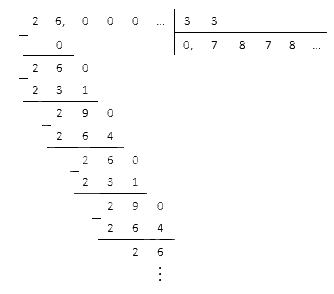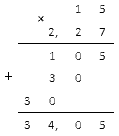Как умножают обыкновенные дроби
Умножение обыкновенных дробей
| Чтобы умножить обыкновенную дробь на натуральное число, нужно ее числитель умножить на это число, а знаменатель оставить без изменения. |
Обратите внимание, если в ответе получается неправильная дробь, то из нее выделяют целую часть.
Если мы умножаем на натуральное число, которое можно сократить с числом, стоящим в знаменателе, то сначала выполняют сокращение, а затем умножение (такой ход действий облегчает вычисления).
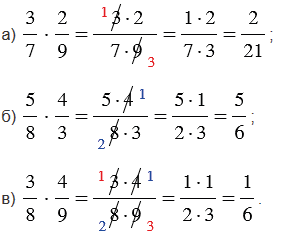
Если мы перемножаем дроби, у которых можно сократить числитель первой и знаменатель второй дроби и (или) знаменатель первой и числитель второй дроби, то сначала выполняют сокращение, а затем умножение (такой ход действий облегчает вычисления).
Умножение смешанных чисел
| Чтобы выполнить умножение смешанных чисел, нужно записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей. |
Для обыкновенных дробей, как и для натуральных чисел, выполняются свойства умножения (переместительное свойство умножения, сочетательное свойство умножения, распределительные свойства умножения относительно сложения и относительно вычитания). Также при умножении дроби на ноль (или нуля на дробь) получаем ноль, и при умножении дроби на единицу (или единицы на дробь) получим равную ей дробь.
| Чтобы умножить смешанное число на натуральное число, можно представить смешанное число в виде неправильной дроби, а затем воспользоваться правилом умножения дроби на натуральное число или можно умножить целую часть на натуральное число, далее умножить дробную часть на натуральное число и полученные произведения сложить. |
Нахождение дроби от числа
Примеры:
а) Найти 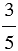
Решение:
б) Найти 0,6 от числа 9.
Решение:
в) Найти 30 % от числа 500.
Решение:
1) 30% = 30 : 100 = 0,30 = 0,3
Взаимно обратные числа
| Два числа, произведение которых равно 1, называют взаимно обратными. |
Примеры:
1) 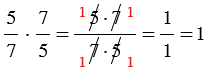
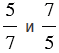
2)
Чтобы определить число обратное смешанному числу, нужно представить это смешанное число в виде неправильной дроби.
Пример:
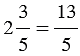
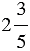
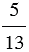
Запомните:
Поделись с друзьями в социальных сетях:
Умножение обыкновенных дробей: правила, примеры, решения
Еще одно действие, которое можно выполнять с обыкновенными дробями, – умножение. Мы попробуем разъяснить его основные правила при решении задач, покажем, как умножается обыкновенная дробь на натуральное число и как правильно выполнить умножение трех обыкновенных дробей и больше.
Как умножить одну обыкновенную дробь на другую
Запишем сначала основное правило:
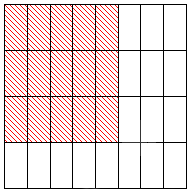
Посмотрим на примере, как правильно применить это правило. Допустим, у нас есть квадрат, сторона которого равна одной числовой единице. Тогда площадь фигуры составит 1 кв. единицу. Если разделить квадрат на равные прямоугольники со сторонами, равными 1 4 и 1 8 числовой единицы, у нас получится, что он теперь состоит из 32 прямоугольников (потому что 8 · 4 = 32 ). Соответственно, площадь каждого из них будет равна 1 32 от площади всей фигуры, т.е. 1 32 кв. единицы.
Далее нам надо выделить цветом часть исходного квадрата так, как это сделано на рисунке:
5 8 · 3 4 = 5 · 3 8 · 4 = 15 32
Разберем решения нескольких задач на умножение обыкновенных дробей.
Решение
Все решение можно записать так:
7 11 · 9 8 = 7 · 9 11 · 8 = 63 88
Если в ответе у нас получилась сократимая дробь, нужно довести вычисление до конца и выполнить ее сокращение. Если же у нас получилась неправильная дробь, из нее надо выделить целую часть.
Решение
Cогласно изученному выше правилу, нам надо умножить числитель на числитель, а знаменатель на знаменатель. Запись решения будет выглядеть так:
4 15 · 55 6 = 4 · 55 15 · 6 = 220 90
Поясним, как это выглядит, используя данные конкретной задачи.
Решение
Запишем вычисления, исходя из правила умножения. У нас получится:
4 15 · 55 6 = 4 · 55 15 · 6
Далее мы можем просто сократить некоторые множители и получить следующее: 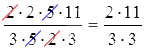
Нам осталось подсчитать несложные произведения в числителе и знаменателе и выделить целую часть из получившейся в итоге неправильной дроби:
2 · 11 3 · 3 = 22 9 = 2 4 9
Числовое выражение, в котором имеет место умножение обыкновенных дробей, обладает переместительным свойством, то есть при необходимости мы можем изменить порядок следования множителей:
a b · c d = c d · a b = a · c b · d
Как перемножить обыкновенную дробь с натуральным числом
Запишем сразу основное правило, а потом попробуем объяснить его на практике.
Понять эту формулу легко, если вспомнить, что любое натуральное число может быть представлено в виде обыкновенной дроби со знаменателем, равным единице, то есть:
a b · n = a b · n 1 = a · n b · 1 = a · n b
Поясним нашу мысль конкретными примерами.
Решение
2 27 · 5 = 2 · 5 27 = 10 27
Ответ: 2 27 · 5 = 10 27
Когда мы перемножаем натуральное число с обыкновенной дробью, то часто приходится сокращать результат или представлять его как смешанное число.
Решение
Также мы могли сократить дробь с помощью разложения числителя и знаменателя на простые множители, и результат получился бы точно таким же.
Числовое выражение, в котором натуральное число умножается на дробь, также обладает свойством перемещения, то есть порядок расположения множителей не влияет на результат:
a b · n = n · a b = a · n b
Как выполнить умножение трех и более обыкновенных дробей
Мы можем распространить на действие умножения обыкновенных дробей те же свойства, которые характерны для умножения натуральных чисел. Это следует из самого определения данных понятий.
Благодаря знанию сочетательного и переместительного свойства можно перемножать три обыкновенные дроби и более. Допустимо переставлять множители местами для большего удобства или расставлять скобки так, как будет легче считать.
Покажем на примере, как это делается.
Перед тем, как начать умножение, мы можем немного облегчить себе задачу и разложить некоторые числа на простые множители для дальнейшего сокращения. Это будет проще, чем сокращать уже готовую дробь, получившуюся в результате.
1 · 12 · 3 · 5 20 · 5 · 7 · 8 = 1 · ( 2 · 2 · 3 ) · 3 · 5 2 · 2 · 5 · 5 · 7 ( 2 · 2 · 2 ) = 3 · 3 5 · 7 · 2 · 2 · 2 = 9 280
Решение
Умножение дробей.
Чтобы правильно умножить дробь на дробь или дробь на число, нужно знать простые правила. Эти правила сейчас разберем подробно.
Умножение обыкновенной дроби на дробь.
Чтобы умножить дробь на дробь необходимо посчитать произведение числителей и произведение знаменателей этих дробей.
Рассмотрим пример:
Мы числитель первой дроби умножаем с числителем второй дроби, также и знаменатель первой дроби умножаем со знаменателем второй дроби.
Умножение дроби на число.
Воспользуемся этим правилом при умножении.
Неправильную дробь \(\frac<20> <7>= \frac<14 + 6> <7>= \frac<14> <7>+ \frac<6> <7>= 2 + \frac<6><7>= 2\frac<6><7>\\\) перевели в смешанную дробь.
Другими словами, при умножении числа на дробь, число умножаем на числитель, а знаменатель оставляем без изменения. Пример:
Умножение смешанных дробей.
Чтобы перемножить смешанные дроби, нужно сначала каждую смешанную дробь представить в виде неправильно дроби, а потом воспользоваться правилом умножения. Числитель умножаем с числителем, знаменатель умножаем со знаменателем.
Умножение взаимно обратных дробей и чисел.
Вопросы по теме:
Как умножить дробь на дробь?
Ответ: произведение обыкновенных дробей является умножение числитель с числителем, знаменатель со знаменателем. Чтобы получить произведение смешанных дробей нужно перевести их в неправильную дробь и перемножить по правилам.
Как выполнить умножение дробей с разными знаменателями?
Ответ: не важно одинаковые или разные знаменатели у дробей, умножение происходит по правилу нахождения произведения числитель с числителем, знаменатель со знаменателем.
Как умножать смешанные дроби?
Ответ: в первую очередь надо перевести смешанную дробь в неправильную дробь и далее находить произведение по правилам умножения.
Как умножить число на дробь?
Ответ: число умножаем с числителем, а знаменатель оставляем тот же.
Пример №1:
Вычислите произведение: а) \(\frac<8> <9>\times \frac<7><11>\) б) \(\frac<2> <15>\times \frac<10><13>\)
Пример №2:
Вычислите произведения числа и дроби: а) \(3 \times \frac<17><23>\) б) \(\frac<2> <3>\times 11\)
Пример №3:
Напишите число обратное дроби \(\frac<1><3>\)?
Ответ: \(\frac<3> <1>= 3\)
Пример №4:
Вычислите произведение двух взаимно обратных дробей: а) \(\frac<104> <215>\times \frac<215><104>\)
Пример №5:
Могут ли взаимно обратные дроби быть:
а) одновременно правильными дробями;
б) одновременно неправильными дробями;
в) одновременно натуральными числами?
Решение:
а) чтобы ответить на первый вопрос приведем пример. Дробь \(\frac<2><3>\) правильная, обратная ей дробь будет равна \(\frac<3><2>\) – неправильная дробь. Ответ: нет.
в) натуральные числа – это числа которые мы используем при счете, например, 1, 2, 3, …. Если возьмем число \(3 = \frac<3><1>\), то обратная ей дробь будет \(\frac<1><3>\). Дробь \(\frac<1><3>\) не является натуральным числом. Если мы переберем все числа, получать обратное число всегда дробь, кроме 1. Если возьмем число 1, то обратная ей дробь будет \(\frac<1> <1>= \frac<1> <1>= 1\). Число 1 натуральное число. Ответ: могут быть одновременно натуральными числами только в одном случае, если это число 1.
Пример №6:
Выполните произведение смешанных дробей: а) \(4 \times 2\frac<4><5>\) б) \(1\frac<1> <4>\times 3\frac<2><7>\)
Решение:
а) \(4 \times 2\frac<4> <5>= \frac<4> <1>\times \frac<14> <5>= \frac<56> <5>= 11\frac<1><5>\\\\ \)
б) \(1\frac<1> <4>\times 3\frac<2> <7>= \frac<5> <4>\times \frac<23> <7>= \frac<115> <28>= 4\frac<3><7>\)
Пример №7:
Могут ли два взаимно обратных числа быть одновременно смешанными числами?
Умножение и деление дробей
В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей»). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.
Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.
Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.
В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь — ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.
Задача. Найдите значение выражения:
По определению имеем:
Умножение дробей с целой частью и отрицательных дробей
Если в дробях присутствует целая часть, их надо перевести в неправильные — и только затем умножать по схемам, изложенным выше.
Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:
До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:
Задача. Найдите значение выражения:
Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:
Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).
Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.
Сокращение дробей «на лету»
Умножение — весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения. Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:
Задача. Найдите значение выражения:
По определению имеем:
Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.
Обратите внимание: в первом случае множители сократились полностью. На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.
Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:
Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.
Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:
Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.
Умножение десятичных дробей: правила, примеры, решения
В рамках этого материала мы коснемся только правил умножения положительных дробей. Случаи с отрицательными разобраны отдельно в статьях об умножении рациональных и действительных чисел.
Умножение десятичных дробей: общие принципы
Сформулируем общие принципы, которых надо придерживаться при решении задач на умножение десятичных дробей.
Вспомним для начала, что десятичные дроби есть не что иное, как особая форма записи обыкновенных дробей, следовательно, процесс их умножения можно свести к аналогичному для дробей обыкновенных. Это правило работает и для конечных, и для бесконечных дробей: после их перевода в обыкновенные с ними легко выполнять умножение по уже изученным нами правилам.
Посмотрим, как решаются такие задачи.
Мы можем использовать метод подсчета столбиком, как и для натуральных чисел.
Для начала приведем исходные дроби к обыкновенным. У нас получится:
Полученную в итоге обыкновенную дробь можно привести к десятичному виду, разделив числитель на знаменатель в столбик:
Если у нас в условии задачи стоят бесконечные непериодические дроби, то нужно выполнить их предварительное округление (см. статью об округлении чисел, если вы забыли, как это делается). После этого можно производить действие умножения с уже округленными десятичными дробями. Приведем пример.
Решение
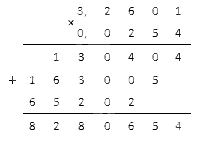
Как умножать десятичные дроби столбиком
Метод подсчета столбиком можно применять не только для натуральных чисел. Если у нас есть десятичные дроби, мы можем умножить их точно таким же образом. Выведем правило:
Умножение десятичных дробей столбиком выполняется в 2 шага:
1. Выполняем умножение столбиком, не обращая внимание на запятые.
2. Ставим в итоговом числе десятичную запятую, отделяя ей столько цифр с правой стороны, сколько оба множителя содержат десятичных знаков вместе. Если в результате не хватает для этого цифр, дописываем слева нули.
Разберем примеры таких расчетов на практике.
Решение
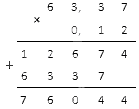
Первым делом выполним умножение чисел, игнорируя десятичные запятые.
Решение
Считаем без учета запятых. Получаем следующее число:
Мы будем ставить запятую, отделяющую 8 цифр с правой стороны, ведь исходные дроби вместе имеют 8 знаков после запятой. Но в нашем результате всего семь цифр, и нам не обойтись без дополнительных нулей:
Как умножить десятичную дробь на 0,001, 0,01, 01, и т.д
Умножать десятичные дроби на такие числа приходится часто, поэтому важно уметь делать это быстро и точно. Запишем особое правило, которым мы будем пользоваться при таком умножении:
Решение
Как перемножить десятичную дробь с натуральным числом
Процесс такого умножения ничем не отличается то действия умножения двух десятичных дробей. Удобно пользоваться методом умножения в столбик, если в условии задачи стоит конечная десятичная дробь. При этом надо учитывать все те правила, о которых мы рассказывали в предыдущем пункте.
Решение
Умножим столбиком исходные числа и отделим два знака запятой.
Если мы выполняем умножение периодической десятичной дроби на натуральное число, надо сначала поменять десятичную дробь на обыкновенную.
Приведем периодическую дробь к виду обыкновенной.
Бесконечные дроби перед подсчетами надо предварительно округлить.
Решение
Округлим до сотых исходную бесконечную десятичную дробь. После этого мы придем к умножению натурального числа и конечной десятичной дроби:
Как умножить десятичную дробь на 1000, 100, 10 и др
Покажем на примере, как именно это делать.
Решение
Приведенное нами правило будет работать так же и в случае с бесконечными десятичными дробями, но здесь следует быть очень внимательным к периоду итоговой дроби, так как в нем легко допустить ошибку.
Если в условиях задачи стоят бесконечные непериодические дроби, которые надо умножать на десять, сто, тысячу и др., не забываем округлить их перед умножением.
Как перемножить десятичную дробь с обыкновенной или со смешанным числом
Чтобы выполнить умножение такого типа, нужно представить десятичную дробь в виде обыкновенной и далее действовать по уже знакомым правилам.
Решение
Если в расчете участвует бесконечная непериодическая дробь, нужно округлить ее до некоторой цифры и уже потом умножать.
Решение