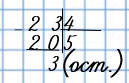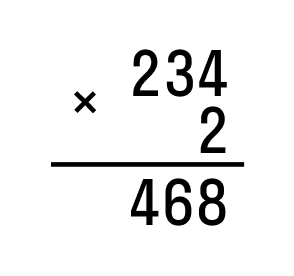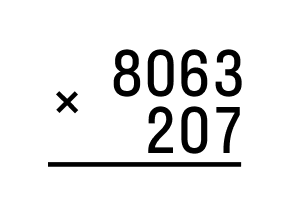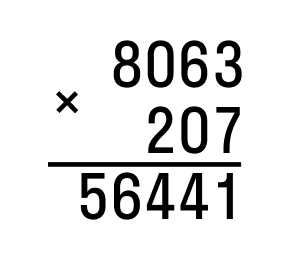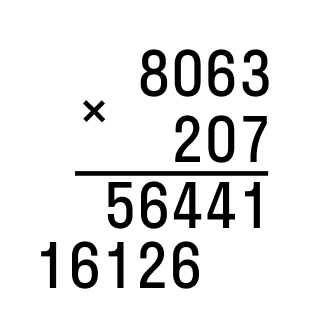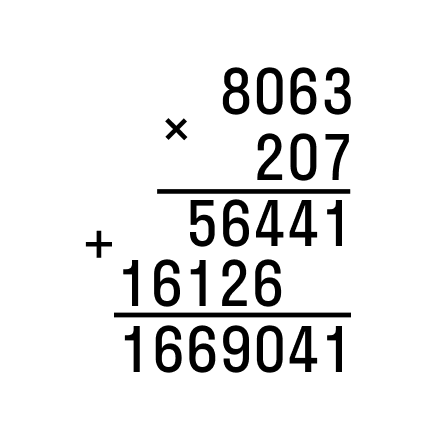Как умножать с остатком
Математика
Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет
С этой картой можно накопить на мечту, жми ⇒
План урока:
На уроке научимся умножать и делить круглые числа, решать задачи на движение в противоположных направлениях.
Начнем с разминки. Чтобы хорошо и быстро умножать и делить многозначные числа, нужно знать на «отлично» таблицу умножения. Проверим? Игра называется «В десяточку!». Вам нужно набрать ровно 10 баллов, чтобы стать победителем. Записывайте в черновик только ответы. Попросите друга читать примеры, так будет быстрее! Правильные ответы найдете в рубрике «Это интересно».
Умножение чисел, оканчивающихся нулями
Решим следующие примеры устно: 721 ∙ 50, 4 500 ∙ 40.
Заменим круглое число произведением двух множителей: 50 = 5 ∙ 10
Число 721 сначала умножим на 5, затем – на 10.
721 ∙ 50 = (721 ∙ 5) ∙10 = 3 605 ∙ 10 = 36 050
Во втором примере сначала число 4 500 представим в виде произведения множителей 45 и 100, затем число 40 – в виде произведения 4 и 10.
4 500 ∙ 40 = 45 ∙ 100 ∙ 4 ∙ 10 = (45 ∙ 4) ∙100 ∙10 =180 ∙100 ∙10 = 180 000
Записи получаются очень длинными, можно и запутаться! Гораздо удобнее записать такие примеры столбиком. Мы знаем, что при умножении многозначных чисел столбиком существуют строгие правила: единицы подписываем под единицами, десятки – под десятками и так далее. Но при умножении круглых чисел от этого строгого правила нужно отступить.
Множители записываем друг под другом так, чтобы нули оказалась в стороне (как бы за чертой).
Попробуйте самостоятельно решить несколько примеров столбиком. Не забывайте о том, что под черту сносим нули обоих множителей.
640 ∙ 200 69 000 ∙ 30 56 700 ∙ 80
Деление чисел, оканчивающихся нулями
Решим устно примеры: 240 : 40, 720 : 80.
Заменим делитель произведением двух чисел: 40 = 4 ∙ 10, 80 = 8 ∙10.
240 : 40 = 240 : (4 ∙ 10) = 240 : 10 : 4 = 6
720 : 80 = 720 : (8 ∙10) = 720 : 10 : 8 = 9
Попробуем решить пример более сложный.
Заменим 60 произведением 6 ∙ 10
1560 : 60 = 1560 : (6 ∙ 10) = 1560 :10 : 6 = 156 : 6
Действительно, 156 разделить на 6 устно трудно. Значит, этот способ здесь не подходит!
Будем делить столбиком.
Теперь самостоятельно поработайте с числами, которые оканчиваются нулями. Устно выполняйте вычисления в первом столбике, письменно – во втором.
640 : 80
210 : 30
720 : 30
1280 : 80
640 : 80 = 640 : (8 ∙ 10) = 640 : 10 : 8 = 8
210 : 30 = 210 : (3 ∙ 10) = 210 : 10 : 3 = 7
Деление с остатком на 10, 100, 1 000
79 : 10 450 : 10 900 : 100 817 : 100 95 000 : 1 000 95 600 : 1 000
Запишем в первый столбик примеры на деление без остатка, а во второй – с остатком.
450 : 10
900 : 100
95 000 : 1 000
79 : 10
817 : 100
95 600 : 1 000
Вспомним, как разделить число на 10, 100, 1 000. При делении на 10 у делимого убираем один нуль, при делении на 100 – убираем два нуля, при делении на 1 000 – убираем три нуля. Очень просто! Решим примеры первого столбика.
450 : 10 = 45
900 : 100 = 9
95 000 : 1 000 = 95
А какое правило действует при делении на 10, 100, 1 000 с остатком?
У делимого не будем убирать цифры, а только лишь отступим (с конца) на одну цифру, если делим на 10, на две – если делим на 100, на три – если делим на 1 000. Вот так:
79 : 10 7 9
817 : 100 8 17
95 600 : 1 000 95 600
Получаем ответ и остаток.
79 : 10 = 7 (ост. 9)
817 : 100 = 8 (ост. 17)
95 600 : 1 000 = 95 (ост. 600)
Сделаем проверку умножением и прибавим остаток.
7 ∙ 10 + 9 = 79
8 ∙100 + 17 = 817
95 ∙ 1 000 + 600 = 95 600
Ребята, помните о том, что при делении остаток должен быть меньше делителя!
Давайте проверим это правило в наших примерах.
Умножение в столбик — удобные способы и примеры решения
Перемножение однозначных чисел мало у кого вызывает затруднение, ведь для решения таких примеров существует специальная таблица.
Вычислять же значения дробей и многозначных чисел в строку бывает довольно затруднительно.
удержать промежуточные результаты в голове порой просто невозможно. Как раз для таких случаев придумано умножение в столбик — этот метод значительно упрощает математические вычисления.
Необходимый минимум
Преимущество использования «столбиков» очевидно — пропадает необходимость считать в уме или всегда держать при себе калькулятор. Даже действительно длинные числа с помощью этого метода умножаются без лишних проблем. Достаточно иметь при себе:
Если же с последним пока ещё возникают затруднения, можно положить её рядом с собой и сверять по ходу решения. Правда, при таком раскладе процесс затянется на какое-то время, а полученный результат желательно перепроверить. Ведь одна маленькая ошибка в начале или середине вычисления сделает ответ заведомо неверным.
Регулярное решение примеров столбиком тренирует внимательность и память ребёнка, учит его концентрироваться на отдельно взятой задаче. Это также удобный способ закрепить базовые математические знания.
Как умножать столбиком
Чтобы научиться решать примеры, необходимо понять и отработать базовый алгоритм.
В целом он достаточно прост:
Метод столбиков не подходит для решения примеров, содержащих корни или возведённые в степень числа.
Прежде чем приступить к вычислениям, «проблемные» цифры нужно преобразовать до целых или десятичных.
Решение базовых примеров
Для большей наглядности стоит привести примеры умножения двузначных и трёхзначных чисел.
Пример 1 — отыскать произведение чисел 58 и 23. Решение задания:
По такому же принципу происходит умножение трёхзначных чисел. Разве что вычисление потребует чуть больше времени, а количество промежуточных результатов увеличится.
Пример 2 — решить выражение 659х854. Пошаговое решение:
При затруднениях в процессе решения можно проверить правильность умножения столбиком онлайн-калькулятором. А также существуют специальные генераторы примеров, которые используют как своеобразный тренажёр для закрепления изученного материала.
Целые числа с нулями
В ситуациях с нулями немного сложнее.
Если нолик «потерялся» где-то в середине, то в процессе решения его следует пропустить. Ведь умножение абсолютно любого числа на 0 в итоге даёт этот же 0. Поэтому можно сразу переходить к следующей цифре и заполнить строку под чертой, отступив не на 1, а на 2 единицы.
Что касается таких чисел как 10, 100, 1200, 12030 и т. п. — суть такая же, но алгоритм решения отличается. Вычисления проводят лишь с цифрами, отличными от нуля. А все «0» на конце чисел просто игнорируются. Хотя после сложения их количество надо подсчитать и добавить к ответу:
Задание 1 — найти произведение чисел 202 и 123. Решение таково:
Задание 2 — вычислить 120х300. Пошаговое решение:
Операции с десятичными дробями
На самом деле умножение десятичных дробей столбиком не слишком сильно отличается от аналогичного действия с числами, у которых есть нули.
В этом случае примеры решают точно так же, как и обычные — про запятую можно временно забыть. Но, когда ответ уже найден, её обязательно нужно восстановить. А для этого надо узнать, сколько цифр после запятой находится у каждого множителя. Их количество складывают, а потом отсчитывают это число с конца ответа.
Задание 1 — вычислить 2,5х3. Пошаговое решение:
Задание 2 — отыскать значение произведения 7,5х2,5. Решение с объяснением:
Если как следует разобраться в теме, юный математик сможет решать даже сложные примеры. Единственный минус метода — большие числа делают вычисления громоздкими, из-за каждой ошибки придётся проверять и править весь пример.
Деление с остатком
Начнём рассмотрение новой темы с решения задачи.
Мама принесла 8 конфет и разделила их поровну между двумя детьми. Сколько конфет получил каждый?
Каждый ребёнок получил по 4 конфеты.
На следующий день мама опять принесла 8 конфет, но в гостях у её детей была ещё одна подружка. Мама опять разделила конфеты поровну, но уже между тремя детьми. Сколько конфет получил каждый ребёнок?
Каждый получил по 2 конфеты и 2 конфеты остались лишними.
Как сделать проверку?
Правило 1
Деление с остатком — это деление одного числа на другое, при котором остаток не равен нулю.
Правило 2
При делении с остатком остаток всегда должен быть меньше делителя.
Порядок решения
1. Нахожу наибольшее число до 14, которое делится на 5 без остатка. Это число 10.
2. Вычитаю из делимого найденное число: 14 − 10 = 4
3. Сравниваю остаток с делителем
Проверка деления с остатком
1. Умножаю неполное частное на делитель.
2. Прибавляю остаток к полученному результату.
3. Сравниваю полученный результат с делимым, он должен быть МЕНЬШЕ.
Деление в столбик
В 23 содержится 5 раз по 4, и ещё остаётся 3.
Решение записывают так:
23 : 4 = 5 (ост. 3) или так:
Поделись с друзьями в социальных сетях:
Как умножать в столбик
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Основные понятия
Во всем мире принято использовать эти десять цифр для записи чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С их помощью создается любое натуральное число.
Название числа напрямую зависит от количества знаков.
Разряд — это позиция, на которой стоит цифра в записи. Их принято отсчитывать с конца.
Разряд единиц — то, чем заканчивается любое число. Разряд десятков — то, что находится перед разрядом единиц. Разряд сотен стоит перед разрядом десятков. На место отсутствующего разряда всегда можно поставить ноль.
Умножение — арифметическое действие, в котором участвуют два аргумента — множители. Результат их умножения называется произведением.
Свойства умножения
От перестановки множителей местами произведение не меняется.
Результат произведения трёх и более множителей не изменится, если любую группу заменить произведением.
Самое главное в процессе вычисления — это знание таблицы умножения. Это сделает подсчет упорядоченным и быстрым.
Важно помнить правило: умножение в столбик с нулями дает в результате ноль:
Алгоритм умножения в столбик
Чтобы понять, как умножать в столбик — рассмотрим действия по шагам:
Запишем пример в строку. Выберем и подчеркнем из двух чисел наименьшее, чтобы не забыть при новой записи поставить его вниз.
Записываем произведение в виде столбика. Сначала наибольший множитель, затем наименьший, тот что мы подчеркнули ранее. Слева ставим соответствующий знак и проводим черту под которой будем записывать ход решения. Важно обратить внимание разряды, чтобы единицы стояли стоять под единицами, десятки под десятками и т. д.
Поэтапно производим необходимые действия. Каждую цифру первого множителя нужно умножить на крайнюю цифру второго. Это действие происходит справа налево: единицы, десятки, сотни.
Если результат получится двузначным, под чертой записывается только последняя его цифра. Остальное переносим в следующий разряд путем сложения со значением, полученным при следующем умножении.
После умножения на единицу второго множителя с остальными цифрами необходимо провести аналогичные манипуляции. Результаты записывать под чертой, сдвигаясь влево на одну позицию.
Складываем то, что нашли и получаем ответ.
Умножение на однозначное число
Для решения задачи по произведению двух натуральных чисел, одно из которых однозначное, а другое — многозначное, нужно использовать способ столбика. Для вычисления воспользуемся последовательностью шагов, которую рассмотрели выше.
Возьмем пример 234 × 2:
Запишем первый множитель, а под ним второй. Соответствующие разряды расположены друг под другом. Двойка находится под четверкой.
Последовательно умножаем каждое число в первом множителе на второй, начиная с единиц и продвигаясь к десяткам и сотням.
Ответ запишем под чертой:
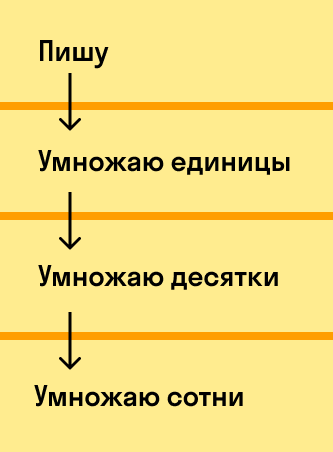
Производить действия необходимо в следующей последовательности:
Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!
Умножение двух многозначных чисел
Если оба множителя — многозначные натуральные числа, нужно действовать следующим образом.
Рассмотрим пример 207 × 8063:
Сначала запишем наибольшее 8063, затем наименьшее 207. Нужно разместить цифры друг под другом справа налево:
Последовательно перемножаем значения разрядов. Результатом является неполное произведение.
Далее перемножаем десятки. Первый множитель умножим на значение разряда десятков второго и т. д. Результат запишем под чертой.
По аналогии действуем с сотыми. Ноль пропускаем в соответствии с правилом. Так получилось второе неполное произведение:
Далее складываем два произведения в столбик.
Получившееся семизначное число — результат умножения исходных натуральных чисел.
Ответ: 8 063 × 207 = 1 669 041.
Примеры на умножение в столбик
Самостоятельное решение задачек помогает быстрее запомнить правила и натренировать скорость. Не важно, в каком классе учится ребенок — в 1, 3 или 4 — эти примеры подойдут всем.
Деление чисел с остатком
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Деление с остатком целых положительных чисел
Деление — это разбиение целого на равные части.
Остаток от деления — это число, которое образуется при делении с остатком. То есть то, что «влезло» и осталось, как хвостик.
Чтобы научиться делить числа с остатком, нужно усвоить некоторые правила. Начнем!
Все целые положительные числа являются натуральными. Поэтому деление целых чисел выполняется по всем правилам деления с остатком натуральных чисел.
Попрактикуемся в решении.
Пример
Разделить 14671 на 54.
Выполним деление столбиком:
Неполное частное равно 271, остаток — 37.
Ответ: 14671 : 54 = 271(остаток 37).
Деление с остатком положительного числа на целое отрицательное
Чтобы легко выполнить деление с остатком положительного числа на целое отрицательное, обратимся к правилу:
В результате деления целого положительного a на целое отрицательное b получаем число, которое противоположно результату от деления модулей чисел a на b. Тогда остаток равен остатку при делении |a| на |b|.
Неполное частное — это результат деления с остатком. Обычно в ответе записывают целое число и рядом остаток в скобках.
Это правило можно описать проще: делим два числа со знаком «плюс», а после подставляем «минус».
Все это значит, что «хвостик», который у нас остается, когда делим положительное число на отрицательное — всегда положительное число.
Алгоритм деления положительного числа на целое отрицательное (с остатком):
Пример
Разделить 17 на −5 с остатком.
Применим алгоритм деления с остатком целого положительного числа на целое отрицательное.
Разделим 17 на − 5 по модулю. Отсюда получим, что неполное частное равно 3, а остаток равен 2. Получим, что искомое число от деления 17 на − 5 = − 3 с остатком 2.
Ответ: 17 : (− 5) = −3 (остаток 2).
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Деление с остатком целого отрицательного числа на целое положительное
Чтобы быстро разделить с остатком целое отрицательное число на целое положительное, тоже придумали правило:
Чтобы получить неполное частное с при делении целого отрицательного a на положительное b, нужно применить противоположное данному числу и вычесть из него 1. Тогда остаток d будет вычисляться по формуле:
d = a − b * c
Из правила делаем вывод, что при делении получается целое неотрицательное число.
Для точности решения применим алгоритм деления а на b с остатком:
Рассмотрим пример, где можно применить алгоритм.
Пример
Найти неполное частное и остаток от деления −17 на 5.
Разделим заданные числа по модулю.
Получаем, что при делении частное равно 3, а остаток 2.
Так как получили 3, противоположное ему −3.
Необходимо отнять единицу: −3 − 1 = −4.
Чтобы вычислить остаток, необходимо a = −17, b = 5, c = −4, тогда:
d = a − b * c = −17 − 5 * (−4) = −17 − (− 20) = −17 + 20 = 3.
Значит, неполным частным от деления является число −4 с остатком 3.
Ответ: (−17) : 5 = −4 (остаток 3).
Деление с остатком целых отрицательных чисел
Сформулируем правило деления с остатком целых отрицательных чисел:
Для получения неполного частного с от деления целого отрицательного числа a на целое отрицательное b, нужно произвести вычисления по модулю, после чего прибавить 1. Тогда можно произвести вычисления по формуле:
d = a − b * c
Из правила следует, что неполное частное от деления целых отрицательных чисел — положительное число.
Алгоритм деления с остатком целых отрицательных чисел:
Пример
Найти неполное частное и остаток при делении −17 на −5.
Применим алгоритм для деления с остатком.
Разделим числа по модулю. Получим, что неполное частное равно 3, а остаток равен 2.
Сложим неполное частное и 1: 3 + 1 = 4. Из этого следует, что неполное частное от деления заданных чисел равно 4.
Для вычисления остатка применим формулу. По условию a = −17, b = −5, c = 4, тогда получим d = a − b * c = −17 − (−5) * 4 = −17 − (−20) = −17 + 20 = 3.
Получилось, что остаток равен 3, а неполное частное равно 4.
Ответ: (−17) : (−5) = 4 (остаток 3).
Деление с остатком с помощью числового луча
Деление с остатком можно выполнить и на числовом луче.
Пример 1
Рассмотрим выражение: 10 : 3.
Отметим на числовом луче отрезки по 3 деления. Видим, что три деления помещаются полностью три раза и одно деление осталось.
Решение: 10 : 3 = 3 (остаток 1).
Пример 2
Рассмотрим выражение: 11 : 3.
Отметим на числовом луче отрезки по 3 деления. Видим, что три деления поместились три раза и два деления осталось.
Решение: 11 : 3 = 3 (остаток 2).
Проверка деления с остатком
Пока решаешь пример, бывает всякое: то в окно отвлекся, то друг позвонил. Чтобы убедиться в том, что все правильно, важно себя проверять. Особенно ученикам 5 класса, которые только начали проходить эту тему.
Формула деления с остатком
a = b * c + d,
где a — делимое, b — делитель, c — неполное частное, d — остаток.
Эту формулу можно использовать для проверки деления с остатком.
Пример
Рассмотрим выражение: 15 : 2 = 7 (остаток 1).
В этом выражении: 15 — это делимое, 2 — делитель, 7 — неполное частное, а 1 — остаток.
Чтобы убедиться в правильности ответа, нужно неполное частное умножить на делитель (или наоборот) и к полученному произведению прибавить остаток. Если в результате получится число, которое равно делимому, то деление с остатком выполнено верно. Вот так:
Теорема о делимости целых чисел с остатком
Если нам известно, что а — это делимое, тогда b — это делитель, с — неполное частное, d — остаток. И они между собой связаны. Эту связь можно описать через теорему о делимости с остатком и показать при помощи равенства.
Теорема
Любое целое число может быть представлено только через целое и отличное от нуля число b таким образом:
где q и r — это некоторые целые числа. При этом 0 ≤ r ≤ b.
Доказательство:
Если существуют два числа a и b, причем a делится на b без остатка, тогда из определения следует, что есть число q, и будет верно равенство a = b * q. Тогда равенство можно считать верным: a = b * q + r при r = 0.
Тогда необходимо взять q такое, чтобы данное неравенством b * q