Как умножать графики функций
Преобразования графиков функций с примерами решения и образцами выполнения
Параллельный перенос, сжатие и растяжение графиков. Построение графиков с модулями.
Графики многих функций можно получить из ранее рассмотренных с помощью элементарных геометрических преобразований: параллельного переноса, сжатия, растяжения, симметричного отображения. Рассмотрим некоторые из этих преобразований. Для каждого из элементарных преобразований предлагается два способа построения графика: с помощью преобразования графика и с помощью преобразования системы координат. Обучающийся должен выбрать тот, который кажется ему проще и овладеть им. В каждом случае считается известным график функции у = f(х).
Параллельный перенос графиков
График функции у = /(x) + Ь получается из графика функции у = f(х) с помощью его переноса на вектор b = (0; b). Действительно, в этом случае ко всем ординатам графика у = f(х) прибавляется величина b, что означает сдвиг графика вдоль оси Оу. Если b > 0, то график функции у = f(х) переносится вверх параллельно оси Oy на b, если b 0 — вниз, если b 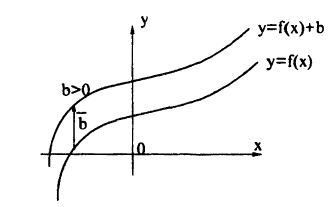
Пример:
График функции у = x² — 1 (рис. 50) смещен на 1 вниз параллельно оси Oy относительно графика функции у = х².
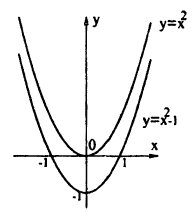
График функции у = f(x+a) получается с помощью переноса графика функции у = f(x) на вектор а = (—а;0). Действительно, перейдя к новым координатам X = х + α, Y = у параллельным переносом вдоль оси Ox на —а, заметим, что относительно новых координат получится исходный график функции Y = f(X). Если а > 0, то старые координаты получаются из новых сдвигом направо вдоль оси Ox на α, т.к. х = X — а. Если же сдвигать график, а не систему координат, то его нужно двигать в противоположном направлении — налево. Итак, если а > 0, то график функции у = f(x) переносится налево параллельно оси Ox на а, если а 0 — вправо, если α 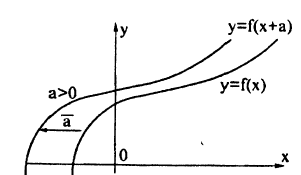
Сжатие и растяжение графиков
График функции у = kf(x), где к ∈ R, получается с помощью ’’растяжения” графика функции у = f(x) в к раз в направлении от оси Ох. ’’Растяжение” здесь понимается как умножение на к ординат всех точек графика у = f(x)∙ При k > 1 это будет действительно растяжение в к раз от оси Ox вдоль оси Оу. При 0 0 можно исправить значения по оси Оу, умножив их на k. При k 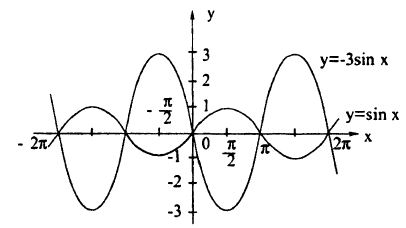
При k > 1 график функции у = f(x) сжимается в k раз к оси Oy вдоль оси Ох; при 0 0 можно исправить значения по оси Ох, поделив их на k. При k 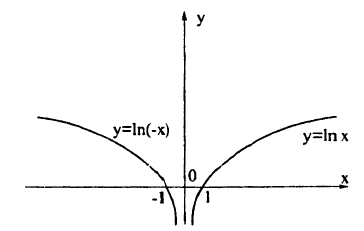
Пользуясь изложенными методами, приведем последовательность преобразований при построении графика функции у = f(kx + b), если дан график функции у = f(x):
Пример:
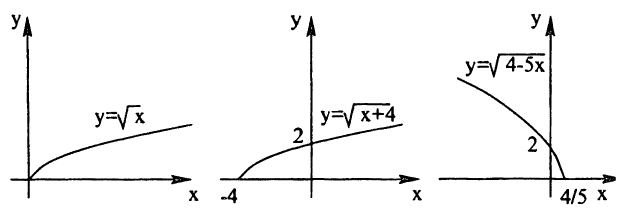
Написать последовательность преобразований и построить график функции у = 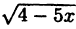
Решение:
Построение графика показано на рис. 55
Замечание:
Теперь понятно, что если функция у = f(x) периодическая с периодом Т, то функция у = К ∙ f(kx + b) + а тоже периодическая с периодом T₁ = 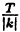
Построение графиков с модулями
График функции у = ∣f(x)∣ получается из графика функции у = f(x) следующим образом (рис. 56)
Действительно, по определению модуля действительного числа имеем:
(5.1)
Таким образом, те участки исходного графика, которые лежат не ниже оси Ox (f(x) ≥ 0), менять не нужно, а для тех участков, которые лежат ниже оси Ох, нужно построить функцию у = —f(x). В соответствии с п. 5.2 это получается симметричным отображением исходного графика относительно оси Ох. Заметим, что полученный график лежит не ниже оси Ох, что естественно, т.к. |f(x)| ≥ 0 для ∀x ∈ D(f).
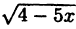
Пример:
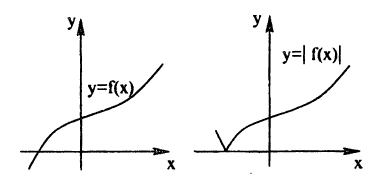
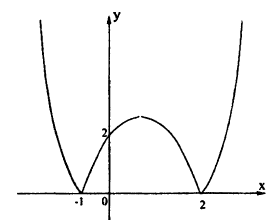
Построение графика функции у = |х² — 1| показано на рис. 57.
График функции у = f (|x|) получается из графика функции у = f(х) следующим образом (рис. 58):
Действительно, по определению модуля действительного числа имеем:
(5.2)
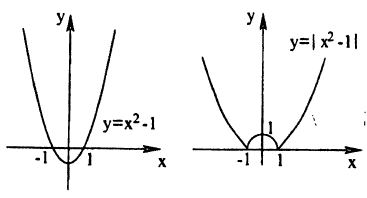
Таким образом, не нужно изменять те участки исходного графика, для которых х ≥ 0, а для х 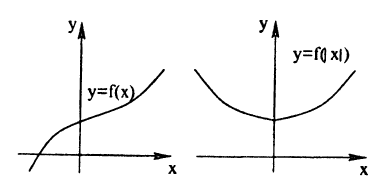
Пример:
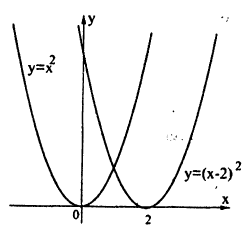
Построение графика функции у = (|x| — 2)² показано на рис. 59
Элементарными методами можно строить эскизы графиков более сложных функций.
Пример:
Построить эскиз графика у =
Решение:
Построение графика показано на рис. 60. Заметим, что график отсутствует там, где sin х 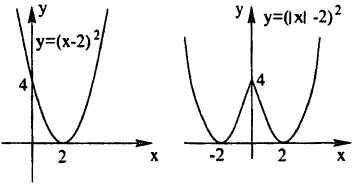
Кроме того, так как √u > и при 0 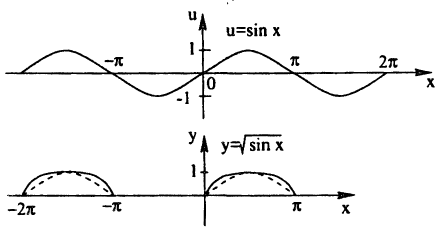
Построение графиков функций с примерами
Пример:
C помощью элементарных преобразований постройте график функции: у = x² — х — 2.
Решение:
Выделим полный квадрат из правой части уравнения функции: у = x² — х — 2 ⇔ y = x²-x+ 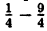
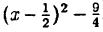
1) y =x²
2) у =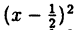
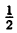
3) у = 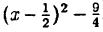
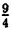
Пример:
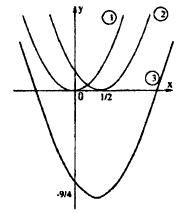
Используя сложение, деление функций, постройте график функции: у = х + 
Решение:
В одних осях координат нарисуем графики следующих функций (рис. 62):
1) у = х,
2) y=
3) y = x + 
Пример:
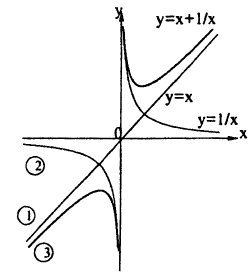
Постройте график сложной функции у = sin² х.
Решение:
В одних осях координат нарисуем графики функций:
1) y = sin x,
2) y = sin² х.
Учитывая, что квадрат числа меньшего единицы, меньше исходного числа, получим график (рис. 63)
Пример:
Постройте график функции в полярной системе координат: r = 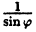
Решение:
Вычислим значения г для некоторых значений 
 | 0 | 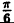 | 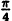 | 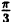 | 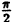 |
| r | ∞ | 2 | 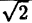 | 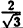 | ∞ |
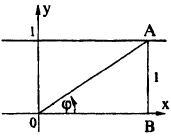
Соединив плавной линией найденные точки, получим линию вдоль оси Ох, проходящую через точку (0;1). Докажем что эта линия — прямая (рис. 64). Действительно: из Δ ОAВ ⇒ cos 
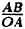
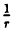
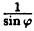
Пример:
Постройте линию, описываемую уравнением, у =
Решение:
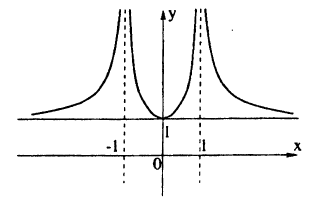
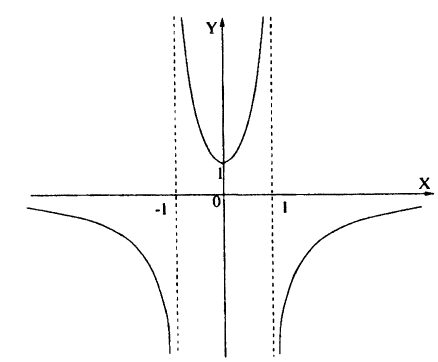
Сначала построим график функции у = 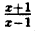
Наконец, строим линию описываемую уравнением у = 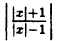
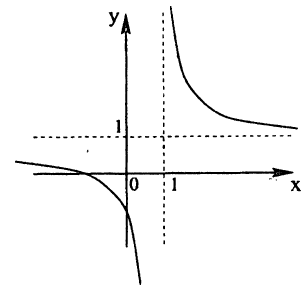
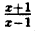
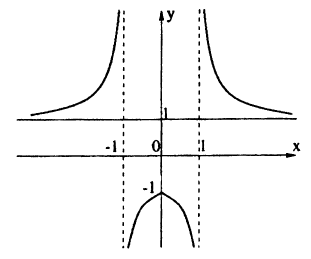
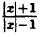
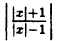
Пример:
Постройте линию, описываемую уравнением у =
Решение:
Для построения графика данного примера сначала постройте график функции у =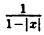
Пример:
Решение:
Для построения графика данного примера сначала постройте график функции у = х² — х — 2. Затем отразите симметрично оси Ox ту часть графика, которая осталась снизу от оси Ох. Затем сотрите ту часть графика, которая расположена в нижней полуплоскости.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Преобразование графиков функций
В этой статье мы расскажем об основных преобразованиях графиков функций. Что нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали. Как задать растяжение графика по горизонтали или вертикали. Как отразить график относительно оси Х или Y.
Но конечно, не только для того, чтобы сдать ЕГЭ. Первая лекция на первом курсе технического или экономического вуза посвящена функциям и графикам. Первые зачеты в курсе матанализа связаны с функциями и графиками.
Начнем со сдвигов графиков по Х и по Y.
Сдвиг по горизонтали.
Пусть функция задана формулой и Тогда график функции сдвинут относительно исходной на а вправо. График функции сдвинут относительно исходной на а влево.
1. Сдвиг по вертикали.
Пусть функция задана формулой и С — некоторое положительное число. Тогда график функции сдвинут относительно исходного на С вверх. График функции сдвинут относительно исходного на С вниз.
Теперь растяжение графика. Или сжатие.
2. Растяжение (сжатие) по горизонтали.
3. Растяжение (сжатие) по вертикали
И отражение по горизонтали.
4. Отражение по горизонтали
График функции симметричен графику функции относительно оси Y.
5. Отражение по вертикали.
График функции симметричен графику функции относительно оси Х.
Друзья, не возникло ли у вас ощущения, что вы все это где-то видели? Да, наверняка видели, если когда-либо редактировали изображения в графическом редакторе на компьютере. Изображение можно сдвинуть (по горизонтали или вертикали). Растянуть (по горизонтали или вертикали). Отразить. И все это мы делаем с графиками функций.
6. Графики функций и
На рисунке изображен график функции Она специально взята такая — несимметричная относительно нуля.
Построим график функции
Конечно же, мы пользуемся определением модуля.
Это мы и видим на графике. Для неотрицательных значений х график остался таким же, как был. А вместо каждого отрицательного х мы взяли противоположное ему положительное число. И поэтому вся та часть графика функции, что лежала слева от оси Х, заменилась на зеркально отраженную правую часть графика.
Теперь график функции Вы уже догадались, что будет. Вся часть графика, лежащая ниже оси Х, зеркально отражается в верхнюю полуплоскость. А верхняя часть графика, лежащая выше оси Х, остается на месте.
Вот самые простые задачи на преобразование графиков.
1. Построим график функции
Это квадратичная парабола, сдвинутая на 3 влево по x и на 1 вниз по y.
2. Построим график функции
Выделим полный квадрат в формуле.
Обратите внимание: график функции пересекает ось y в точке На нашем графике это точка
Алгебра. Урок 5. Графики функций
Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Декартова система координат
Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.
Координатные оси – прямые, образующие систему координат.
Ось абсцисс (ось x ) – горизонтальная ось.
Ось ординат (ось y ) – вертикальная ось.
Функция
Прямая
Линейная функция – функция вида y = a x + b где a и b – любые числа.
Графиком линейной функции является прямая линия.
Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :
Парабола
Гипербола
Характерная особенность гиперболы в том, что у неё есть асимптоты.
Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.
Ось x – горизонтальная асимптота гиперболы
Ось y – вертикальная асимптота гиперболы.
На графике асимптоты отмечены зелёной пунктирной линией.
0″ height=»346″ width=»346″ sizes=»(max-width: 346px) 100vw, 346px» data-srcset=»/wp-content/uploads/2017/01/Гипербола-1.png 346w,/wp-content/uploads/2017/01/Гипербола-1-150×150.png 150w,/wp-content/uploads/2017/01/Гипербола-1-300×300.png 300w,/wp-content/uploads/2017/01/Гипербола-1-176×176.png 176w,/wp-content/uploads/2017/01/Гипербола-1-60×60.png 60w, https://epmat.ru/wp-content/uploads/2017/01/Гипербола-1.png»>
Если k 0, ветви гиперболы проходят через II и IV четверти.
Квадратный корень
Функция y = x имеет следующий график:
Возрастающие/убывающие функции
То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)
Примеры возрастающих функций:
То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).
Примеры убывающих функций:
Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.
Элементарные функции и их графики
Понятие функции — одно из ключевых в математике. О нём подробно рассказано в статье «Что такое функция».
И конечно, в задачах части 2 Профильного ЕГЭ по математике без них не обойтись. А если вы выбрали технический или экономический вуз — первая же лекция по матанализу будет посвящена именно элементарным функциями и их графикам.
Но это не всё. Математические функции, изучением которых мы занимаемся, — это не что-то такое выдуманное или существующее только в замкнутом пространстве учебника. Они являются отражением реальных взаимосвязей и процессов, происходящих в природе и обществе.
Существует всего пять типов элементарных функций:
2. Показательные
Это функции вида y = a x
4. Тригонометрические
В их формулах присутствуют синусы, косинусы, тангенсы и котангенсы.
Элементарными они называются потому, что из них, как из элементов, получаются все остальные, встречающиеся в школьном курсе. Например, y = x 2 · e x — произведение квадратичной и показательной функций; y = sin(a x ) — сложная функция, то есть комбинация двух функций — показательной и тригонометрической.
Графики и свойства основных элементарных функций следует знать наизусть.

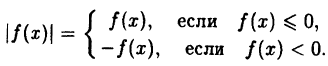
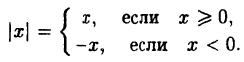
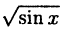
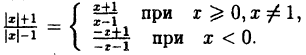
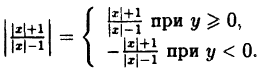

















 , где n — целое? Потому что функция y = sinx — периодическая, то есть каждое свое значение принимает бесконечно много раз.
, где n — целое? Потому что функция y = sinx — периодическая, то есть каждое свое значение принимает бесконечно много раз.