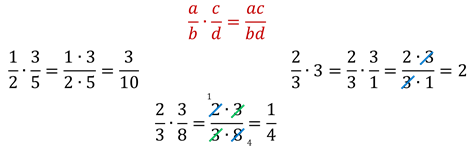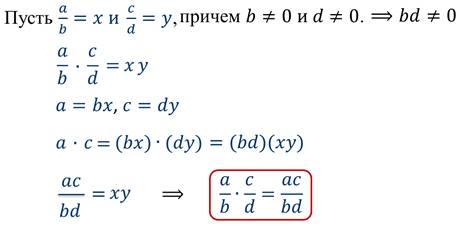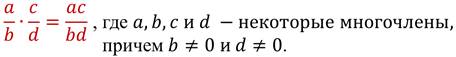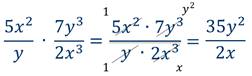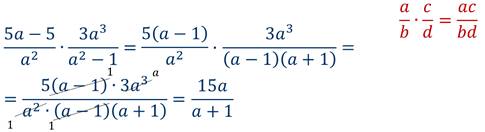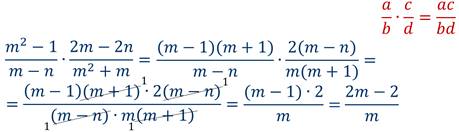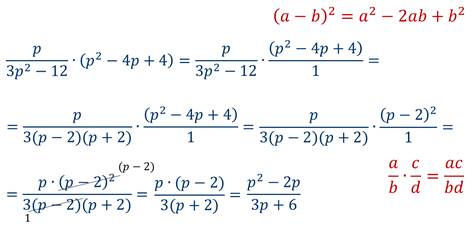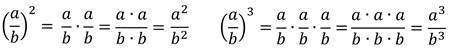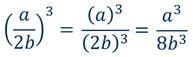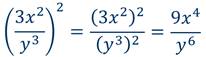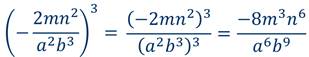Как умножать дроби со степенями
Умножение и деление алгебраических дробей
Умножение дробей
Чтобы умножить одну алгебраическую дробь на другую, надо умножить числитель первой дроби на числитель второй дроби (полученное произведение будет числителем результата) и отдельно умножить знаменатель первой дроби на знаменатель второй (полученное произведение будет знаменателем результата).
Правило умножения алгебраических дробей в виде формулы:
| a | · | c | = | ac | , |
| b | d | bd |
Пример. Выполнить умножение алгебраических дробей:
Решение: Перед тем, как приступать к умножению дробей, желательно разложить их числители и знаменатели на множители — это поможет сократить алгебраическую дробь, которая получится в результате:
Теперь сокращаем полученную дробь:
Чтобы умножить многочлен на алгебраическую дробь или алгебраическую дробь на многочлен, надо умножить многочлен на числитель дроби, а знаменатель оставить без изменений.
Пример. Выполнить умножение многочлена на алгебраическую дробь:
Разложим числитель на множители и сократим дробь:
Правило умножения алгебраической дроби на многочлен (или умножение многочлена на алгебраическую дробь) в виде формулы:
| a · | b | = | ab | или | b | · a | = | ab | , |
| c | c | c | c |
Возведение алгебраических дробей в степень
Чтобы возвести в степень алгебраическую дробь, надо возвести в эту степень отдельно её числитель и отдельно знаменатель.
Правило возведения алгебраических дробей в степень в виде формулы:
| ( | a | ) n = | a n | . |
| b | b n |
Пример. Выполнить возведение в степень:
| а) ( | a 2 | ) 3 ; б) (- | 2x 3 | ) 2 | . |
| b | y 2 |
| а) ( | a 2 | ) 3 = | (a 2 ) 3 | = | a 6 | ; |
| b | (b) 3 | b 3 |
| б) (- | 2x 3 | ) 2 = | (2x 3 ) 2 | = | 4x 6 | . |
| y 2 | (y 2 ) 2 | y 4 |
Деление дробей
Чтобы разделить одну алгебраическую дробь на другую, надо дробь, выступающую в качестве делителя, заменить на обратную ей дробь и после этого умножить первую дробь на вторую.
Правило деления алгебраических дробей в виде формулы:
| a | : | c | = | a | · | d | = | ad | . |
| b | d | b | c | bc |
Следовательно, частное двух дробей равно произведению первой дроби и перевёрнутой второй дроби.
Пример. Выполнить деление алгебраических дробей:
Решение: Переворачиваем делитель и умножаем дроби по правилам умножения:
Теперь можно приступать к сокращению полученной дроби:
Чтобы разделить многочлен на алгебраическую дробь, надо перевернуть дробь и выполнить умножение многочлена на полученную дробь по правилам умножения.
Правило деления многочлена на алгебраическую дробь в виде формулы:
| a : | b | = a · | c | = | ac | . |
| c | b | b |
Пример. Выполнить деление:
Чтобы разделить алгебраическую дробь на многочлен, надо представить многочлен в виде дроби и перевернуть её, затем выполнить умножение дробей по правилам умножения.
Правило деления алгебраической дроби на многочлен в виде формулы:
Сложение, вычитание, умножение, и деление степеней
Сложение и вычитание степеней
Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками.
Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.
Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.
Но степени различных переменных и различные степени одинаковых переменных, должны слагаться их сложением с их знаками.
Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.
Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.
Умножение степеней
Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.
Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.
Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.
Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.
Если умножается сумма и разница двух чисел, возведённых в квадрат, результат будет равен сумме или разнице этих чисел в четвёртой степени.
Деление степеней
Числа со степенями могут быть поделены, как и другие числа, путем отнимая от делимого делителя, или размещением их в форме дроби.
При делении степеней с одинаковым основанием их показатели вычитаются..
| Делимое | y 2m | 8a n+m | 12(b + y) n |
| Делитель | y m | 4a m | 3(b + y) 3 |
| Результат | y m | 2a n | 4(b +y) n-3 |
Или:
y 2m : y m = y m
8a n+m : 4a m = 2a n
12(b + y) n : 3(b + y) 3 = 4(b +y) n-3
Необходимо очень хорошо усвоить умножение и деление степеней, так как такие операции очень широко применяются в алгебре.
Примеры решения примеров с дробями, содержащими числа со степенями
Умножение, деление и возведение дробей в степень
Вы будете перенаправлены на Автор24
С алгебраическими дробями можно проводить любые математические операции, такие как сравнение, сложение, вычитание, умножение, деление и возведение в степень.
Умножение алгебраических дробей
Алгебраические дроби умножают по тому же правилу, что и обыкновенные дроби
т.е. при умножении алгебраических дробей необходимо умножить числители исходных дробей и знаменатели исходных дробей
Для нахождения произведения воспользуемся правилом умножения дробей, тогда получим
Для нахождения произведения воспользуемся правилом умножения дробей, тогда получим
Деление алгебраических дробей
Алгебраические дроби делят по тому же правилу, что и обыкновенные дроби
т.е. при делении алгебраических дробей необходимо первую дробь оставить без изменений, деление заменить на умножение, а вторую дробь изменить на обратную, затем произвести умножение полученных дробей
Воспользуемся правилом, тогда получим
Применив данную формулу, получим:
Тогда дробь примет вид
Теперь заметим, что числитель и знаменатель дроби содержит одинаковое выражение х-4, на которое можно сократить дробь
Готовые работы на аналогичную тему
Возведение в степень алгебраических дробей
Алгебраические дроби возводят в степень по тому же правилу, что и обыкновенные дроби
т.е. при возведении алгебраических дробей в степень необходимо числитель возвести в указанную степень и знаменатель возвести в степень.
Сначала воспользуемся правилом возведения дроби в степень, т.е. необходимо числитель возвести в указанную степень и знаменатель возвести в степень
Теперь воспользуемся правилом возведения степени в степень в числителе
В знаменателе воспользуемся правилом возведения в степень произведения
А теперь преобразуем по свойству возведения в отрицательный показатель степени:
Тогда исходная дробь примет вид
Теперь воспользуемся правилом возведения в степень дроби, тогда получим:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 29 04 2021
Умножение дробей. Возведение дроби в степень
Урок 5. Алгебра 8 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Умножение дробей. Возведение дроби в степень»
Для начала давайте вспомним правило умножения обыкновенных дробей.
Для того чтобы умножить дробь на дробь, надо числитель умножить на числитель, а знаменатель на знаменатель и первое произведение записать в числителе новой дроби, второе – в знаменателе.
Аналогичным образом происходит умножение рациональных дробей. Давайте докажем, что это правило на самом деле действует при умножении рациональных дробей.
Иначе говоря, докажем, что произведение двух рациональных дробей тождественно равно дроби, у которой числитель равен произведению числителей, а знаменатель – произведению знаменателей перемножаемых дробей при любых допустимых значениях переменных, кроме b равное нулю и d равное нулю.
Получили, что равенство верно при любых допустимых значениях переменных, т.е. является тождеством.
Правило умножения рациональных дробей:
Чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе – знаменателем дроби.
В буквенном виде это правило записывают так:
Это правило выполняется и когда произведение трёх и более рациональных дробей.
Прежде чем выполнять умножение рациональных дробей, полезно их числители и знаменатели разложить на множители. Это облегчит сокращение той рациональной дроби, которая получится в результате умножения.
Пример 1: умножить дроби.
Пример 2: умножить дроби.
Пример 3: Представить произведение дробей в виде рациональной дроби.
Пример 4: выполнить умножение.
Теперь рассмотрим, как выполняется возведение рациональной дроби в степень.
Проверим это равенство на конкретных примерах.
Правило возведения рациональной дроби в степень:
Чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе, а второй в знаменателе дроби.
Пример 5: возвести в третью степень дробь.
Пример 6: возвести во вторую степень дробь.
Чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе – знаменателем дроби.
Чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе, а второй в знаменателе дроби.
Дробная степень числа
Дробный показатель
Число с дробным показателем степени равно корню с показателем, равным знаменателю, и подкоренным числом в степени, равной числителю.
Чтобы разобраться, почему число в дробной степени равно корню, надо вспомнить правило извлечения корня из степени:
Чтобы извлечь корень из степени, надо показатель степени разделить на показатель корня:
Следовательно, если показатель степени не делится на показатель корня, то получается дробная степень:
Поэтому извлечение корня всегда может быть заменено возведением в степень.
Действия над степенями с дробными показателями
Действия над степенями с дробными показателями совершаются по тем же правилам, которые установлены для степеней с целым показателем.
При доказательстве этого положения, будем сначала предполагать, что члены дробей: 

В частном случае n или q могут равняться единице.
При умножении дробных степеней с одинаковыми основаниями их показатели складываются:
При делении дробных степеней с одинаковыми основаниями из показателя делимого вычитается показатель делителя:
Чтобы возвести степень в другую степень, в случае дробных показателей, достаточно перемножить показатели степеней:
Чтобы извлечь корень из дробной степени, достаточно показатель степени разделить на показатель корня:
Правила действий применимы не только к положительным дробным показателям, но и к отрицательным.