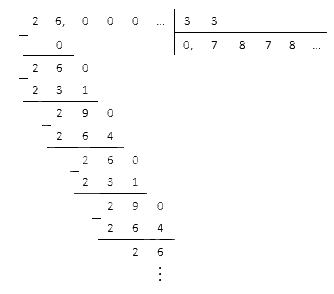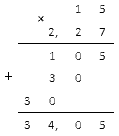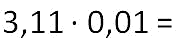Как умножать числа с запятыми

Правило умножения десятичных дробей на натуральные числа

Умножение десятичных дробей — общие принципы

Десятичная дробь — форма записи обыкновенной дроби, у которой знаменатель равен 10, 100, 1000 и т.д.

Числа со знаменателями 10, 100, 1000 и т.д. записывают без знаменателя. Сначала пишут целую часть, а потом числитель дробной части. Целую часть отделяют от дробной части запятой.

Например, вместо 5 7 10 пишут 5,7 (читают: «5 целых 7 десятых»).

Вместо 3 17 100 пишут 3,17 (читают: «3 целых 17 сотых»).

Десятичные дроби перемножают как целые числа, на запятые внимания не обращают. В результате отделяют запятой столько цифр справа, сколько их стоит после запятой во всех множителях вместе.

Задания подобного плана выполняют по следующему алгоритму:

В двух множителях три цифры после запятой. Нужно отделить три цифры справа в результате и поставить запятую.

Умножение десятичной дроби на обыкновенную дробь или смешанное число

Для того, чтобы умножить десятичную дробь на обыкновенную дробь, необходимо:

Для того, чтобы умножить десятичную дробь на смешанное число, необходимо:

Умножение десятичной дроби на натуральное число

Произведение десятичной дроби и натурального числа — сумма слагаемых, каждое из которых равно этой дроби, а количество слагаемых определяется натуральным числом.

Выражение представляют в виде суммы, в которой слагаемое 0,25 повторяется четыре раза:

Для того, чтобы умножить десятичную дробь на натуральное число, необходимо:

Алгоритм, как ставить запятую, правила переноса

Для того, чтобы в результате умножения правильно поставить запятую, надо:

При умножении десятичной дроби на 10, 100, 1000 и т. д. запятую в десятичной дроби переносят вправо на столько цифр, сколько нулей стоит в множителе после единицы.

Если количество цифр в десятичной дроби после запятой меньше количества нулей после единицы, то нужно:

При умножении десятичной дроби на 0,1; 0,01; 0,001 и т. д. переносят запятую влево на столько цифр, сколько нулей стоит перед единицей в множителе. Нуль целых также учитываем.

Примеры решения задач

Для объяснения решения действуем по алгоритму:

6 5 × 3 4 = 6 × 3 5 × 4 :

Чтобы умножить десятичную дробь на смешанное число:

Решаем пример по схеме:

Запятую в десятичной дроби переносим вправо на две цифры, так как в множителе после единицы стоит два нуля.

Запятую переносим влево на четыре цифры, так как в множителе перед единицей стоит четыре нуля.

Чтобы решить уравнение, нужно найти его корни или доказать, что корней нет.

Для закрепления навыков умножения десятичных дробей используют математические тренажеры.

Источник

Умножение десятичных дробей: правила, примеры, решения

В рамках этого материала мы коснемся только правил умножения положительных дробей. Случаи с отрицательными разобраны отдельно в статьях об умножении рациональных и действительных чисел.

Умножение десятичных дробей: общие принципы

Сформулируем общие принципы, которых надо придерживаться при решении задач на умножение десятичных дробей.

Вспомним для начала, что десятичные дроби есть не что иное, как особая форма записи обыкновенных дробей, следовательно, процесс их умножения можно свести к аналогичному для дробей обыкновенных. Это правило работает и для конечных, и для бесконечных дробей: после их перевода в обыкновенные с ними легко выполнять умножение по уже изученным нами правилам.

Посмотрим, как решаются такие задачи.

Мы можем использовать метод подсчета столбиком, как и для натуральных чисел.

Для начала приведем исходные дроби к обыкновенным. У нас получится:

Полученную в итоге обыкновенную дробь можно привести к десятичному виду, разделив числитель на знаменатель в столбик:

Если у нас в условии задачи стоят бесконечные непериодические дроби, то нужно выполнить их предварительное округление (см. статью об округлении чисел, если вы забыли, как это делается). После этого можно производить действие умножения с уже округленными десятичными дробями. Приведем пример.

Решение

Как умножать десятичные дроби столбиком

Метод подсчета столбиком можно применять не только для натуральных чисел. Если у нас есть десятичные дроби, мы можем умножить их точно таким же образом. Выведем правило:

Умножение десятичных дробей столбиком выполняется в 2 шага:

1. Выполняем умножение столбиком, не обращая внимание на запятые.

2. Ставим в итоговом числе десятичную запятую, отделяя ей столько цифр с правой стороны, сколько оба множителя содержат десятичных знаков вместе. Если в результате не хватает для этого цифр, дописываем слева нули.

Разберем примеры таких расчетов на практике.

Решение

Первым делом выполним умножение чисел, игнорируя десятичные запятые.

Решение

Считаем без учета запятых. Получаем следующее число:

Мы будем ставить запятую, отделяющую 8 цифр с правой стороны, ведь исходные дроби вместе имеют 8 знаков после запятой. Но в нашем результате всего семь цифр, и нам не обойтись без дополнительных нулей:

Как умножить десятичную дробь на 0,001, 0,01, 01, и т.д

Умножать десятичные дроби на такие числа приходится часто, поэтому важно уметь делать это быстро и точно. Запишем особое правило, которым мы будем пользоваться при таком умножении:

Решение

Как перемножить десятичную дробь с натуральным числом

Процесс такого умножения ничем не отличается то действия умножения двух десятичных дробей. Удобно пользоваться методом умножения в столбик, если в условии задачи стоит конечная десятичная дробь. При этом надо учитывать все те правила, о которых мы рассказывали в предыдущем пункте.

Решение

Умножим столбиком исходные числа и отделим два знака запятой.

Если мы выполняем умножение периодической десятичной дроби на натуральное число, надо сначала поменять десятичную дробь на обыкновенную.

Приведем периодическую дробь к виду обыкновенной.

Бесконечные дроби перед подсчетами надо предварительно округлить.

Решение

Округлим до сотых исходную бесконечную десятичную дробь. После этого мы придем к умножению натурального числа и конечной десятичной дроби:

Как умножить десятичную дробь на 1000, 100, 10 и др

Покажем на примере, как именно это делать.

Решение

Приведенное нами правило будет работать так же и в случае с бесконечными десятичными дробями, но здесь следует быть очень внимательным к периоду итоговой дроби, так как в нем легко допустить ошибку.

Если в условиях задачи стоят бесконечные непериодические дроби, которые надо умножать на десять, сто, тысячу и др., не забываем округлить их перед умножением.

Как перемножить десятичную дробь с обыкновенной или со смешанным числом

Чтобы выполнить умножение такого типа, нужно представить десятичную дробь в виде обыкновенной и далее действовать по уже знакомым правилам.

Решение

Если в расчете участвует бесконечная непериодическая дробь, нужно округлить ее до некоторой цифры и уже потом умножать.

Решение

Источник

Дроби. Умножение десятичных дробей.

Умножение десятичных дробей производят в 3 этапа:

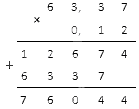
1. Десятичные дроби записываются в столбик и умножают как обычные числа.

2. Считаем число знаков после запятой у 1-ой десятичной дроби и у 2-ой. Их число складываем.

3. В итоговом результате отсчитываем справа налево такое число цифр, сколько получилось их в пункте выше, и ставим запятую.

Правила умножения десятичных дробей.

1. Умножить, не обращая внимания на запятую.

2. В произведении отделяем после запятой такое количество цифр, сколько их после запятых в обоих множителях вместе.

Умножая десятичную дробь на натуральное число, необходимо:

1. Умножить числа, не обращая внимания на запятую;

2. В результате ставим запятую так, чтобы справа от нее было столько цифр, сколько в десятичной дроби.

Умножение десятичных дробей столбиком.

Рассмотрим на примере:

Записываем десятичные дроби в столбик и умножаем их как натуральные числа, не обращая внимания на запятые. Т.е. 3,11 мы рассматриваем как 311, а 0,01 как 1.

Отсчитываем справа налево четыре знака у результата. В итоговом результате цифр меньше, чем нужно отделить запятой. В этом случае необходимо слева дописать не хватающее количество нулей.

В нашем случае не достает 1-ой цифры, поэтому дописываем слева 1 ноль.

Умножая любую десятичную дробь на 10, 100, 1000 и так далее, запятая в десятичной дроби переносится вправо на столько знаков, сколько нулей после единицы.

Для умножения десятичной дроби на 0,1; 0,01; 0,001; и так далее, нужно в этой дроби перенести запятую влево на столько знаков, сколько нулей перед единицей.

Источник

Умножение десятичных дробей: правила, примеры

В данной публикации мы рассмотрим, каким образом десятичную дробь можно умножить на натуральное целое число или другую десятичную дробь. Также разберем примеры для закрепления теоретического материала.

Умножение десятичной дроби на натуральное число

Делитель – 10, 100, 1000, 10000 и т.д.

Чтобы умножить десятичную дробь на натуральное число 10, 100, 1000 и т.д., просто переносим запятую-разделитель вправо на столько нулей, сколько содержит это число.

Пример 1

Объяснение: Т.к. в числе 10 всего один ноль, то и запятую переносим на одну позицию вправо.

Пример 2

Объяснение: Т.к. в числе 100 два нуля, то запятую переносим на две позиции.

Пример 3

Объяснение: В числе 10 один ноль, следовательно, десятичный разделитель сдвигаем на одну позицию.

Пример 4

Объяснение: В числе 1000 три нуля, значит разделитель сдвигаем на три позиции.

Примечание: если количество нулей и, соответственно, позиций переноса разделителя больше, чем цифр после запятой, значит дописываем оставшиеся нули в конце полученного результата. Это работает и в обратную сторону (см. Пример 7 ниже).

Пример 5

Объяснение: В числе 1000 три нуля, следовательно разделитель переносим на две позиции и дописываем один ноль в конце найденного числа.

Делитель – любое число

Чтобы умножить десятичную дробь на любое натуральное целое число, отбрасываем запятую и выполняем умножение, как будто имеем дело не с дробью, а с обычным числом. Затем отсчитываем с конца полученного результата столько цифр, сколько было в дробной части исходной десятичной дроби, и ставим в этом месте запятую.

Пример 6: найдем произведение чисел 5,68 и 8.

Убираем запятую в числе 5,68 и умножаем его на 8:
568 ⋅ 8 = 4544

Отсчитываем две цифры с конца и добавляем запятую-разделитель, т.е.:

Примечание: Если десятичная дробь меньше 1 (т.е. целая часть равна 0), то отбросив запятую, мы не учитываем при умножении ноль/нули, которые идут в начале.

Пример 7: умножим число 0,089 на 7.

Убираем запятую в числе 0,089 и, отбросив нули, умножаем его на 7:
89 ⋅ 7 = 623

Здесь обратная ситуация рассмотренной ранее в Примере 5. С конца отсчитываем 3 цифры, ставим запятую и добавляем ноль слева от нее, т.е.:

Произведение десятичных дробей

Чтобы умножить одну десятичную дробь на другую, выполняем практически те же самые действия, что и описанные в разделе выше – убираем запятые, на этот раз в обеих дробях, и умножаем их как обычные числа. Затем отсчитываем с конца найденного результата столько цифр, сколько их было вместе в дробных частях обоих множителей, и пишем запятую.

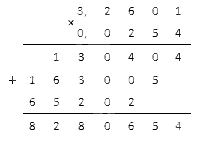
Пример 8: найдем, сколько будет 5,615 ⋅ 2,14.

5615 ⋅ 214 = 1201610

Отсчитать с конца нужно 5 цифр, т.к. в первом множителе после запятой было три цифры, во втором – две (5 = 3 + 2). Т.е.:

5,615 ⋅ 2,14 = 12,01610 = 12,0161

Пример 9: вычислим, сколько будет 0,24 ⋅ 3,17.

Отсекаем запятой 4 цифры с конца и получаем ответ – 0,7608.

Источник

Умножение десятичных дробей

Умножение десятичных дробей происходит в три этапа.

Десятичные дроби записывают в столбик и умножают как обыкновенные числа.

Считаем количество знаков после запятой у первой десятичной дроби и у второй. Их количество складываем.

В полученном результате отсчитываем справа налево столько же цифр, сколько получилось их в пункте выше и ставим запятую.

Как умножать десятичные дроби

Отсчитываем справа налево 4 знака (цифры) у полученного числа. В полученном результате цифр меньше, чем нужно отделить запятой. В таком случае нужно слева приписать недостающее число нулей.

У нас не хватает одной цифры, поэтому приписываем слева один ноль.

При умножении любой десятичной дроби на 10; 100; 1000 и т.д. запятая в десятичной дроби перемещается вправо на столько знаков, сколько нулей стоит после единицы.

Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т.д., надо в этой дроби перенести запятую влево на столько знаков, сколько нулей стоит перед единицей.

Считаем и ноль целых!

Источник