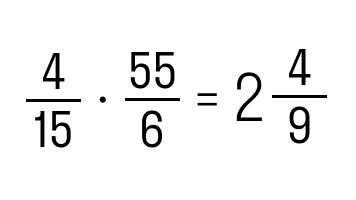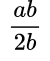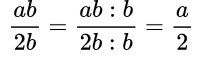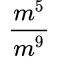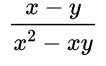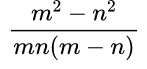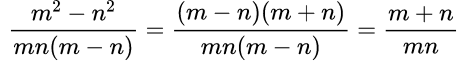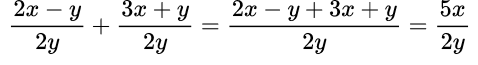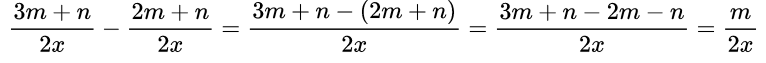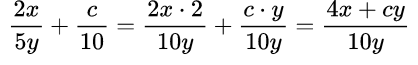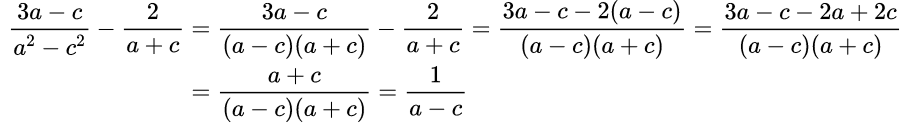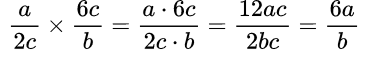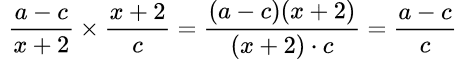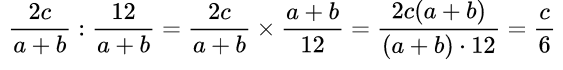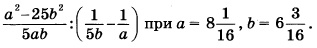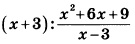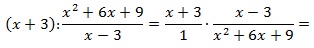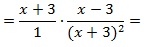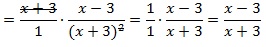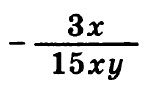Как умножать буквенные дроби
Умножение алгебраических дробей
При умножении алгебраических дробей используют правила умножения обыкновенных дробей.
Правило умножения алгебраических дробей
Рассмотрим пример умножения алгебраических дробей.
При сокращении алгебраических дробей используют правила сокращения алгебраических дробей.
Рассмотрим еще один пример умножения алгебраических дробей, которые содержат многочлены и в числителе, и в знаменателе.
При умножении алгебраических дробей, которые содержат многочлены и в числителе, и в знаменателе, заключайте многочлены в скобки целиком.
Неправильно
Правильно
Как умножить алгебраическую дробь на одночлен (букву)
Рассмотрим пример умножения алгебраической дроби на одночлен.
Представим одночлен « 21z 5 » как алгебраическую дробь со знаменателем « 1 ». Это можно сделать, так как при делении на « 1 » получается тот же самый одночлен.
При умножении алгебраической дроби не забывайте использовать правило знаков.
Рассмотрим пример умножения двух отрицательных алгебраических дробей.
Перед тем как перемножить алгебраические дроби, определим итоговый знак по правилу знаков: « минус на минус дает плюс ».
Значит, итоговым знаком произведения будет знак « + ».
Умножение и деление алгебраических дробей
В этой статье мы продолжаем изучение основных действий, которые можно выполнять с алгебраическими дробями. Здесь мы рассмотрим умножение и деление: сначала выведем нужные правила, а затем проиллюстрируем их решениями задач.
Как правильно делить и умножать алгебраические дроби
Чтобы выполнить умножение алгебраических дробей или разделить одну дробь на другую, нам нужно использовать те же правила, что и для обыкновенных дробей. Вспомним их формулировки.
Когда нам надо умножить одну обыкновенную дробь на другую, мы выполняем отдельно умножение числителей и отдельно знаменателей, после чего записываем итоговую дробь, расставив по местам соответствующие произведения. Пример такого вычисления:
2 3 · 4 7 = 2 · 4 3 · 7 = 8 21
А когда нам надо разделить обыкновенные дроби, мы делаем это с помощью умножения на дробь, обратную делителю, например:
2 3 : 7 11 = 2 3 · 11 7 = 22 7 = 1 1 21
Умножение и деление алгебраических дробей выполняется в соответствии с теми же принципами. Сформулируем правило:
Чтобы перемножить две и более алгебраические дроби, нужно перемножить отдельно числители и знаменатели. Результатом будет дробь, в числителе которой будет стоять произведение числителей, а в знаменателе – произведение знаменателей.
Для того чтобы разделить одну алгебраическую дробь на другую, нужно выполнить умножение первой дроби на дробь, обратную второй.
Отдельно остановимся на том, что такое обратная алгебраическая дробь. Она представляет из себя такую дробь, которая при умножении на исходную дает в итоге единицу. То есть такие дроби будут аналогичны взаимно обратным числам. Иначе можно сказать, что обратная алгебраическая дробь состоит из таких же значений, что и исходная, однако числитель и знаменатель у нее меняются местами. Так, по отношению к дроби a · b + 1 a 3 дробь a 3 a · b + 1 будет обратной.
Решение задач на умножение и деление алгебраических дробей
В этом пункте мы посмотрим, как правильно применять озвученные выше правила на практике. Начнем с простого и наглядного примера.
Решение
Сначала выполним умножение. Согласно правилу, нужно отдельно перемножить числители и знаменатели:
1 x + y · 3 · x · y x 2 + 5 = 1 · 3 · x · y ( x + y ) · ( x 2 + 5 )
Мы получили новый многочлен, который нужно привести к стандартному виду. Заканчиваем вычисления:
1 · 3 · x · y ( x + y ) · ( x 2 + 5 ) = 3 · x · y x 3 + 5 · x + x 2 · y + 5 · y
Теперь посмотрим, как правильно разделить одну дробь на другую. По правилу нам надо заменить это действие умножением на обратную дробь x 2 + 5 3 · x · y :
1 x + y : 3 · x · y x 2 + 5 = 1 x + y · x 2 + 5 3 · x · y
Приведем полученную дробь к стандартному виду:
1 x + y · x 2 + 5 3 · x · y = 1 · x 2 + 5 ( x + y ) · 3 · x · y = x 2 + 5 3 · x 2 · y + 3 · x · y 2
Решение
Перед тем, как вычислять произведение, разложим на отдельные множители числитель первой исходной дроби и знаменатель второй. Для этого нам потребуются формулы сокращенного умножения. Вычисляем:
У нас получилась дробь, которую можно сократить:
О том, как это делается, мы писали в статье, посвященной сокращению алгебраических дробей.
Перемножив одночлен и многочлен в знаменателе, мы получим нужный нам результат:
Вот запись всего решения без пояснений:
В некоторых случаях исходные дроби перед умножением или делением удобно преобразовать, чтобы дальнейшие вычисления стали быстрее и проще.
После всех преобразований можем наконец перейти непосредственно к делению алгебраических дробей:
Как умножить или разделить алгебраическую дробь на многочлен
Решение
Начнем с замены многочлена дробью, далее действуем согласно основному правилу.
Умножение дробей: теория и практика
Понятие дроби
Дробь — одна из форм представления числа в математике. Это запись, в которой a и b являются числами или выражениями. Существует два формата записи:
Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление — в 5 классе уже это знают.
Дроби могут быть двух видов:
Дробь называют правильной, когда ее числитель меньше знаменателя:
Неправильной — ту, у которой числитель больше знаменателя или равен ему:
Такое число называют смешанным, читают как «пять целых одна четвертая», а записывают так: 5 1\4.
Основные правила дробей
Умножение дробных чисел
Рассмотрим несколько вариантов умножения обыкновенных дробей.
Как умножить дробь на дробь
Числитель равен произведению числителей обеих дробей, а знаменатель равен произведению знаменателей:
Важно проверить возможность сокращения — так решать будет легче:
Как умножить смешанные дроби
Преобразовать смешанные числа в неправильные, перемножить числители и знаменатели, при необходимости сократить и перевести в смешанную дробь.
Как умножить дробь на натуральное число
Метод 1. Числитель умножить на натуральное число, а знаменатель оставить без изменения. Если в результате произведения получилась неправильная дробь, нужно выделить целую часть, то есть превратить неправильную в смешанную.
Метод 2. Знаменатель разделить на натуральное число, а числитель оставить прежним.
Этот способ будет удобнее предыдущего, если знаменатель делится на натуральное число без остатка.
Решение задач
Ребятам в 5 и 6 классе нужно практиковаться как можно чаще, чтобы решать такие примеры быстро и легко.
Задание 1. Выполнить умножение 2/17 на 5.
Как решаем: перемножим числитель и натуральное число.
Ответ:
Задание 2. Выполнить умножение 4/15 и 55/6.
Как решаем:
Ответ:
Задание 3. Выполнить умножение одной целой трех седьмых на шесть.
Как решаем:
Ответ:
Онлайн-курсы по математике для детей и подростков — прекрасный способ разобраться в новом материале и закрепить его на практике.
Умножение и деление алгебраических дробей
Умножение дробей
Чтобы умножить одну алгебраическую дробь на другую, надо умножить числитель первой дроби на числитель второй дроби (полученное произведение будет числителем результата) и отдельно умножить знаменатель первой дроби на знаменатель второй (полученное произведение будет знаменателем результата).
Правило умножения алгебраических дробей в виде формулы:
| a | · | c | = | ac | , |
| b | d | bd |
Пример. Выполнить умножение алгебраических дробей:
Решение: Перед тем, как приступать к умножению дробей, желательно разложить их числители и знаменатели на множители — это поможет сократить алгебраическую дробь, которая получится в результате:
Теперь сокращаем полученную дробь:
Чтобы умножить многочлен на алгебраическую дробь или алгебраическую дробь на многочлен, надо умножить многочлен на числитель дроби, а знаменатель оставить без изменений.
Пример. Выполнить умножение многочлена на алгебраическую дробь:
Разложим числитель на множители и сократим дробь:
Правило умножения алгебраической дроби на многочлен (или умножение многочлена на алгебраическую дробь) в виде формулы:
| a · | b | = | ab | или | b | · a | = | ab | , |
| c | c | c | c |
Возведение алгебраических дробей в степень
Чтобы возвести в степень алгебраическую дробь, надо возвести в эту степень отдельно её числитель и отдельно знаменатель.
Правило возведения алгебраических дробей в степень в виде формулы:
| ( | a | ) n = | a n | . |
| b | b n |
Пример. Выполнить возведение в степень:
| а) ( | a 2 | ) 3 ; б) (- | 2x 3 | ) 2 | . |
| b | y 2 |
| а) ( | a 2 | ) 3 = | (a 2 ) 3 | = | a 6 | ; |
| b | (b) 3 | b 3 |
| б) (- | 2x 3 | ) 2 = | (2x 3 ) 2 | = | 4x 6 | . |
| y 2 | (y 2 ) 2 | y 4 |
Деление дробей
Чтобы разделить одну алгебраическую дробь на другую, надо дробь, выступающую в качестве делителя, заменить на обратную ей дробь и после этого умножить первую дробь на вторую.
Правило деления алгебраических дробей в виде формулы:
| a | : | c | = | a | · | d | = | ad | . |
| b | d | b | c | bc |
Следовательно, частное двух дробей равно произведению первой дроби и перевёрнутой второй дроби.
Пример. Выполнить деление алгебраических дробей:
Решение: Переворачиваем делитель и умножаем дроби по правилам умножения:
Теперь можно приступать к сокращению полученной дроби:
Чтобы разделить многочлен на алгебраическую дробь, надо перевернуть дробь и выполнить умножение многочлена на полученную дробь по правилам умножения.
Правило деления многочлена на алгебраическую дробь в виде формулы:
| a : | b | = a · | c | = | ac | . |
| c | b | b |
Пример. Выполнить деление:
Чтобы разделить алгебраическую дробь на многочлен, надо представить многочлен в виде дроби и перевернуть её, затем выполнить умножение дробей по правилам умножения.
Правило деления алгебраической дроби на многочлен в виде формулы:
Алгебраические дроби
теория по математике 📈 алгебраические выражения
Любая обыкновенная дробь называется алгебраической дробью, так как она представляет собой деление, записанное с помощью дробной черты. В алгебраической дроби могут встречаться не только числа, но и буквенные выражения.
Примеры алгебраических дробей:
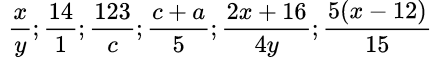
Сокращение алгебраической дроби
Сократить алгебраическую дробь – это значит разделить числитель и знаменатель на одно и то же выражение, на их общий множитель (одночлен, его степень или многочлен) – применяется основное свойство дроби. Причем и числитель, и знаменатель должны содержать множители.
Пример №1. Сократим дробь:
В числителе и знаменателе дроби мы видим переменную b, на которую и разделим каждую часть дроби:
Промежуточные действия можно не записывать, а выполнять устно.
Пример №2. Сократим дробь:
Здесь содержатся степени с одинаковым основанием, поэтому, необходимо помнить еще и правило деления степеней с одинаковым основанием (основание остается прежним, а показатели степеней вычитаем). Сократим дробь на меньшую степень – на m 5 :
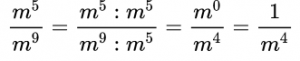
В каждой части дроби содержатся разные многочлены, поэтому сократить пока дробь мы не можем, так как нет множителей. Значит, по возможности, мы должны найти выражение, которое можно разложить на множители, это знаменатель, так как можем вынести за скобки общий множитель х(х – у). Только потом мы можем сократить дробь на одно и то же выражение – многочлен (х – у).
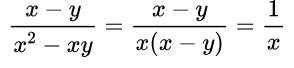
Здесь мы видим, что в числителе многочлен, а в знаменателе произведение одночленов и многочлена, причем многочлены различны. Значит, надо сделать так, чтобы числитель и знаменатель содержали одинаковые множители. Числитель можно разложить на множители по формуле разности квадратов, то есть m 2 – n 2 =(m–n)(m+n), затем сократить дробь на одно и то же выражение (m–n).
Сложение и вычитание алгебраических дробей с одинаковым знаменателем
При сложении и вычитании алгебраических дробей с одинаковыми знаменателями знаменатель остается прежним, а числители складывают или вычитают (из числителя первой вычитают числитель второй дроби).
Пример №5. Выполним сложение дробей:
Здесь одинаковые знаменатели, поэтому записываем его, а числители складываем: при сложении видим подобные слагаемые, которые приводим и получаем в числителе 5х.
Пример №6. Выполним вычитание дробей:
В знаменатель записываем 2х, а из числителя первой дроби вычитаем числитель второй дроби, при этом не забываем вычитаемое взять в скобки, если оно является многочленом. Затем раскрываем скобки, помня о том, что необходимо поменять знаки на противоположные, так как перед ними стоит знак «минус». Затем приводим подобные слагаемые и получаем новый числитель.
Сложение и вычитание алгебраических дробей с разными знаменателями
Чтобы сложить или вычесть дроби с разными знаменателями, необходимо:
Пример №7. Выполнить сложение дробей:
Чтобы найти общий знаменатель, надо найти для чисел 5 и 10 наименьшее общее кратное (наименьшее число, которое делится и на 5, и на 10), это число 10. В первом знаменателе есть еще множитель – переменная у, поэтому также берем у для общего знаменателя. Таким образом, у нас есть два множителя 10 и у, это и есть наш общий знаменатель.
Теперь находим дополнительный множитель к каждой дроби. Для этого общий знаменатель 10у делим на первый знаменатель 5у, получим 2, значит, умножаем на 2 первый числитель 2х. Для второй дроби 10у делим на 10, получаем у, умножаем на него числитель второй дроби – с. Получаем в числителе 4х+су.
Пример №8. Выполнить вычитание дробей:
Здесь знаменатели дробей различные многочлены, поэтому надо рассмотреть каждый. Первый знаменатель – это формула сокращенного умножения, по ней можно разложить на множители данный многочлен а 2 – с 2 =(а–с)(а+с). Второй знаменатель представляет собой простой многочлен, который нельзя разложить на множители. Составим новый знаменатель, состоящий из разных выражений – это (а–с)(а+с).
Находим дополнительные множители: к первой дроби дополнительного множителя нет, так как новый общий знаменатель – это полностью знаменатель первой дроби. А ко второй дроби это будет выражение (а – с). Поэтому умножаем числитель 2 на (а – с).
Приводим подобные слагаемые, а полученную дробь сокращаем на выражение (а+с).
Умножение алгебраических дробей
Чтобы перемножить алгебраические дроби, надо числитель перемножить с числителем, а знаменатель со знаменателем. При необходимости выполнить сокращение алгебраической дроби, используя правило.
Пример №9. Выполнить умножение дробей:
Здесь перемножаем числители и знаменатели, полученную дробь сокращаем на 2с.
Пример №10. Выполнить умножение дробей:
Здесь в числителях и знаменателях — многочлены. Поэтому при записи умножения обязательно заключаем их в скобки. При этом мы видим, что числитель и знаменатель содержат одинаковые множители – многочлены (х+2), поэтому можно сократить дробь на этот многочлен.
Деление алгебраических дробей
Чтобы разделить одну алгебраическую дробь на другую, надо первую дробь умножить на дробь, обратную второй (то есть умножить на дробь, у которой числитель равен знаменателю второй дроби, а знаменатель числителю второй дроби). Далее – выполнить умножение дробей по уже известному алгоритму.
Пример №11. Выполнить деление дробей:
Здесь выполним деление по алгоритму: перейдем от деления к умножению на дробь, обратную делителю. Сократим полученную дробь на выражение (a+b) и на 2.
Найдите значение выражения:
Упрощение заданного выражения нужно начать с преобразований в скобках. Здесь следует привести дроби к общему знаменателю:

затем 1) сокращаем дроби на 5ab; 2) в числителе первой дроби раскладываем выражение, используя формулу сокращенного умножения для разности квадратов:
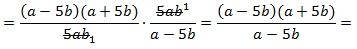


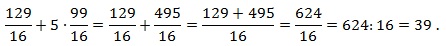
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения при x = 12:
Выполним тождественные преобразования выражения, чтобы упростить его. 1-й шаг – переход от деления дробей к их умножению:
далее в знаменателе второй дроби сворачиваем выражение по формуле сокращенного умножения (используем ф-лу для квадрата суммы):
теперь сокращаем выражение (в числителе первой дроби и в знаменателе второй) и приходим к окончательно упрощенному виду:
Подставляем числовое значение для х в полученное выражение и находим результат:
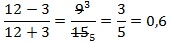
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения
В первую очередь в заданиях такого типа необходимо упростить выражение, а затем подставить числа. Приведем выражение к общему знаменателю — это b, для этого умножим первое слагаемое на b, после этого получим в числителе:
Приведем подобные слагаемые — это 9b² и — 9b², в числителе остается 5a. Запишем конечную дробь:
Вычислим её значение, подставив числа из условия:
pазбирался: Даниил Романович | обсудить разбор | оценить
Найдите значение выражения:
Итак, в данном задании при вычитании дробей нам необходимо привести их к общему знаменателю. Общий знаменатель — это 15 x y, для этого необходимо первую дробь домножить на 5 y — и числитель и знаменатель, естественно:
Далее, после того как дроби приведены к общему знаменателю, можно производить вычисления. Вычислим числитель:
5 y — (3 x + 5 y) = 5 y — 3 x — 5 y = — 3 x
Тогда дробь примет вид:
Выполнив простые сокращения числителя и знаменателя на 3 и на x, получим: — 1/5 y
Подставим значение y = 0,5: — 1 / (5 • 0,5) = — 1 / 2,5 = — 0,4
pазбирался: Даниил Романович | обсудить разбор | оценить