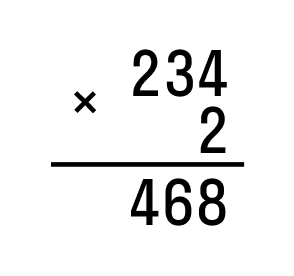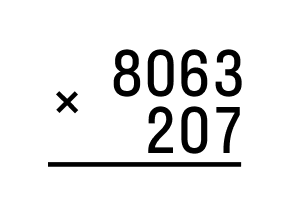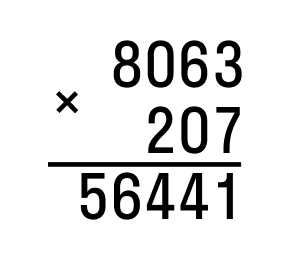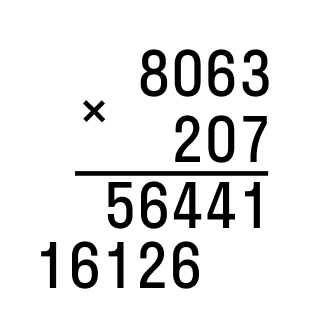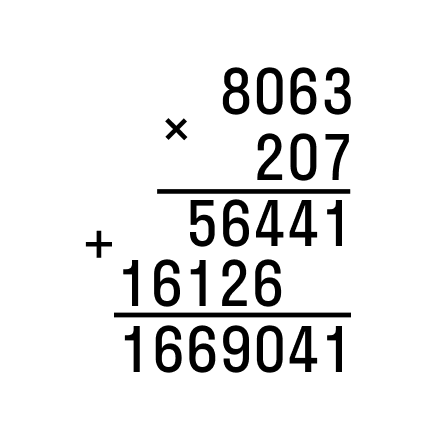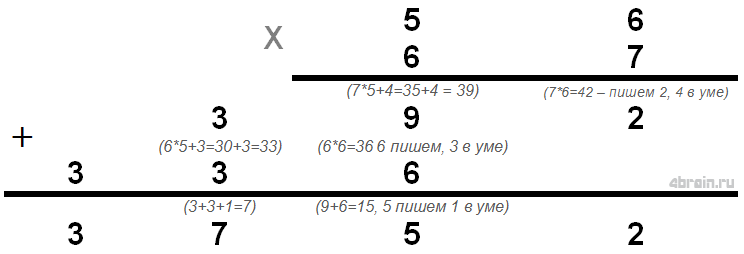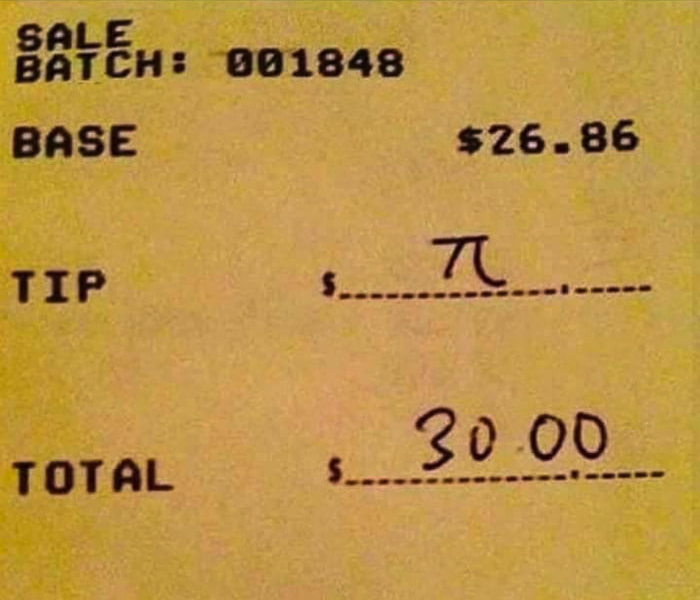Как умножать 2 значные числа

Как умножать в столбик

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Основные понятия

Во всем мире принято использовать эти десять цифр для записи чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. С их помощью создается любое натуральное число.

Название числа напрямую зависит от количества знаков.

Разряд — это позиция, на которой стоит цифра в записи. Их принято отсчитывать с конца.

Разряд единиц — то, чем заканчивается любое число. Разряд десятков — то, что находится перед разрядом единиц. Разряд сотен стоит перед разрядом десятков. На место отсутствующего разряда всегда можно поставить ноль.

Умножение — арифметическое действие, в котором участвуют два аргумента — множители. Результат их умножения называется произведением.

Свойства умножения

От перестановки множителей местами произведение не меняется.

Результат произведения трёх и более множителей не изменится, если любую группу заменить произведением.

Самое главное в процессе вычисления — это знание таблицы умножения. Это сделает подсчет упорядоченным и быстрым.

Важно помнить правило: умножение в столбик с нулями дает в результате ноль:

Алгоритм умножения в столбик

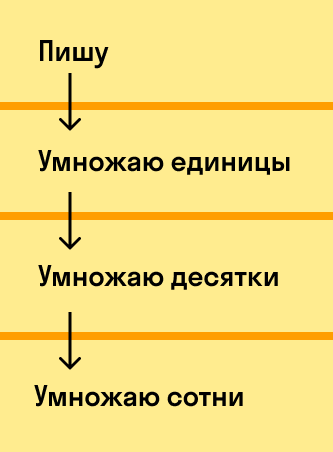
Чтобы понять, как умножать в столбик — рассмотрим действия по шагам:

Запишем пример в строку. Выберем и подчеркнем из двух чисел наименьшее, чтобы не забыть при новой записи поставить его вниз.

Записываем произведение в виде столбика. Сначала наибольший множитель, затем наименьший, тот что мы подчеркнули ранее. Слева ставим соответствующий знак и проводим черту под которой будем записывать ход решения. Важно обратить внимание разряды, чтобы единицы стояли стоять под единицами, десятки под десятками и т. д.

Поэтапно производим необходимые действия. Каждую цифру первого множителя нужно умножить на крайнюю цифру второго. Это действие происходит справа налево: единицы, десятки, сотни.

Если результат получится двузначным, под чертой записывается только последняя его цифра. Остальное переносим в следующий разряд путем сложения со значением, полученным при следующем умножении.

После умножения на единицу второго множителя с остальными цифрами необходимо провести аналогичные манипуляции. Результаты записывать под чертой, сдвигаясь влево на одну позицию.

Складываем то, что нашли и получаем ответ.

Умножение на однозначное число

Для решения задачи по произведению двух натуральных чисел, одно из которых однозначное, а другое — многозначное, нужно использовать способ столбика. Для вычисления воспользуемся последовательностью шагов, которую рассмотрели выше.

Возьмем пример 234 × 2:

Запишем первый множитель, а под ним второй. Соответствующие разряды расположены друг под другом. Двойка находится под четверкой.

Последовательно умножаем каждое число в первом множителе на второй, начиная с единиц и продвигаясь к десяткам и сотням.

Ответ запишем под чертой:

Производить действия необходимо в следующей последовательности:

Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!

Умножение двух многозначных чисел

Если оба множителя — многозначные натуральные числа, нужно действовать следующим образом.

Рассмотрим пример 207 × 8063:

Сначала запишем наибольшее 8063, затем наименьшее 207. Нужно разместить цифры друг под другом справа налево:

Последовательно перемножаем значения разрядов. Результатом является неполное произведение.

Далее перемножаем десятки. Первый множитель умножим на значение разряда десятков второго и т. д. Результат запишем под чертой.

По аналогии действуем с сотыми. Ноль пропускаем в соответствии с правилом. Так получилось второе неполное произведение:

Далее складываем два произведения в столбик.

Получившееся семизначное число — результат умножения исходных натуральных чисел.

Ответ: 8 063 × 207 = 1 669 041.

Примеры на умножение в столбик

Самостоятельное решение задачек помогает быстрее запомнить правила и натренировать скорость. Не важно, в каком классе учится ребенок — в 1, 3 или 4 — эти примеры подойдут всем.

Источник

Как быстро умножать двузначные числа в уме?

Умение мгновенно считать в уме может стать бесценным подспорьем в работе и в условиях скоростных темпов жизни современного человека.

Как быстро умножать большие числа, как овладеть такими полезными навыками? У большинства вызывает затруднения устное перемножение двузначных чисел на однозначные. А о сложных арифметических расчетах и говорить нечего. Но при желании способности, заложенные в каждом человеке, можно развить. Регулярные тренировки, немного усилий и применение, разработанных учеными, эффективных методик позволят достичь потрясающих результатов.

Выбираем традиционные методы

Проверенные десятилетиями способы перемножения двузначных чисел не теряют своей актуальности. Простейшие приемы помогают миллионам обычных школьников, учащихся специализированных ВУЗов и лицеев, а также людям, занимающимся саморазвитием, усовершенствовать вычислительное мастерство.

Умножение с помощью разложения чисел

Наиболее легким способом, как быстро научиться умножать большие числа в уме, является перемножение десятков и единиц. Сначала умножаются десятки двух чисел, затем поочередно единицы и десятки. Четыре полученных числа суммируются. Для использования этого метода важно уметь запоминать результаты перемножения и складывать их в уме.

Умножение в столбик в уме

Приведенные выше способы умножения универсальны. Но знание более эффективных алгоритмов для некоторых чисел намного сократит количество расчетов.

Это, пожалуй, самый простой способ, который используется для умножения любых двузначных чисел на 11.

Достаточно между цифрами множителя вставить их сумму:
13*11 = 1(1+3)3 = 143

Если в скобках получается число больше 10, то к первой цифре добавляется единица, а из суммы в скобках вычитается 10.
28*11 = 2 (2+8) 8 = 308

Умножение больших чисел

Поделитесь этим постом с друзьями

Источник

Урок 3. Традиционное умножение в уме

Давайте рассмотрим, как можно умножать двузначные числа, используя традиционные методы, которым нас обучают в школе. Некоторые из этих методов, могут позволить вам быстро перемножать в уме двузначные числа при достаточной тренировке. Знать эти методы полезно. Однако важно понимать, что это лишь вершина айсберга.

В данном уроке рассмотрены наиболее популярные приемы умножения двузначных чисел.

Первый способ – раскладка на десятки и единицы

Самым простым для понимания способом умножения двузначных чисел является тот, которому нас научили в школе. Он заключается в разбиении обоих множителей на десятки и единицы с последующим перемножением получившихся четырех чисел. Этот метод достаточно прост, но требует умения удерживать в памяти одновременно до трех чисел и при этом параллельно производить арифметические действия.

Проще такие примеры решаются в 3 действия. Сначала умножаются десятки друг на друга. Потом складываются 2 произведения единиц на десятки. Затем прибавляется произведение единиц. Схематично это можно описать так:

Для максимально быстрого эффекта потребуется хорошее знание таблицы умножения чисел до 10, умение складывать числа (до трехзначных), а также способность быстро переключать внимание с одного действия на другое, держа предыдущий результат в уме. Последний навык удобно тренировать путем визуализации совершаемых арифметических операций, когда вы должны представлять себе картинку вашего решения, а также промежуточные результаты.

Вывод. Не трудно убедиться в том, что этот способ не является самым эффективным, то есть позволяющим при наименьших действиях получить правильный результат. Следует принять во внимание другие способы.

Второй способ – арифметические подгонки

Приведение примера к удобному виду является достаточно распространенным способом счета в уме. Подгонять пример удобно, когда вам нужно быстро найти примерный или точный ответ. Желание подгонять примеры под определенные математические закономерности часто воспитывается на математических кафедрах в университетах или в школах в классах с математическим уклоном. Людей учат находить простые и удобные алгоритмы решения различных задач. Вот некоторые примеры подгонки:

Пример 49*49 может решаться так: (49*100)/2-49. Сначала считается 49 на сто – 4900. Затем 4900 делится на 2, что равняется 2450, затем вычитается 49. Итого 2401.

Произведение 56*92 решается так: 56*100-56*2*2*2. Получается: 56*2= 112*2=224*2=448. Из 5600 вычитаем 448, получаем 5152.

Этот способ может оказаться эффективнее предыдущего только в случае, если вы владеете устным счетом на базе перемножения двузначных чисел на однозначные и можете держать в уме одновременно несколько результатов. К тому же приходится тратить время на поиск алгоритма решения, а также уходит много внимания за правильным соблюдением этого алгоритма.

Вывод. Способ, когда вы стараетесь умножить 2 числа, раскладывая их на более простые арифметические процедуры, отлично тренирует ваши мозги, но связан с большими мысленными затратами, а риск получить неправильный результат выше, чем при первом методе.

56*67 – посчитаем в столбик.

Наверное, счет столбиком содержит максимальное количество действий и требует постоянно держать в уме вспомогательные числа. Но его можно упростить. Во втором уроке рассказывалось, что важно уметь быстро умножать однозначные числа на двузначные. Если вы уже умеете это делать на автомате, то счет в столбик в уме для вас будет не таким уж и трудным. Алгоритм таков

Первое действие: 56*7 = 350+42=392 – запомните и не забывайте до третьего действия.

Второе действие: 56*6=300+36=336 (ну или 392-56)

Третье действие: 336*10+392=3360+392=3 752 – тут посложнее, но вы можете начинать называть первое число, в котором уверены – «три тысячи…», а пока говорите, складывайте 360 и 392.

Вывод: счет в столбик напрямую сложен, но вы можете, при наличии навыка быстрого умножения двузначных чисел на однозначные, его упросить. Добавьте в свой арсенал и этот метод. В упрощенном виде счет в столбик является некоторой модификацией первого метода. Что лучше – вопрос на любителя.

Как можно заметить, ни один из описанных выше способов не позволяет считать в уме достаточно быстро и точно все примеры умножения двузначных чисел. Нужно понимать, что использование традиционных способов умножения для счета в уме не всегда является рациональным, то есть позволяющим при наименьших усилиях достигать максимального результата.

Источник

Как умножать двузначные числа: в столбец и в уме

Умножение двузначных чисел – навык, крайне необходимый для нашей повседневной жизни. Люди постоянно сталкиваются с потребностью перемножить что-либо в уме: ценник в магазине, массу продуктов или размер скидки. Но как умножать двузначные числа быстро и без проблем? Давайте разберемся.

Как умножить двузначное число на однозначное?

Начнем с простой задачи – как умножать двузначные числа на однозначные.

Для начала, двузначное число – это такое число, которое состоит из определенного количества десятков и единиц.

Вам будет интересно: University of California Los Angeles: описание, факультеты и рейтинг

Для того чтобы умножить двузначное число на однозначное в столбец, нужно написать нужное двузначное число, а под ним соответствующее однозначное. Далее следует поочередно умножить на заданное число сначала единицы, а потом – десятки. Если при умножении единиц получилось число больше 10, то количество десятков нужно просто перенести в следующий разряд, прибавив их.

Умножение двузначных чисел на десятки

Умножение двузначных чисел на десятки – задача ненамного сложнее, чем умножение на однозначные числа. Основной порядок действий остается тем же:

Как перемножить два двузначных числа?

После того как вы полностью разобрались с умножением двузначных и однозначных чисел, можно начинать думать, как умножать столбиком двузначные числа друг на друга. На самом деле это действие тоже не должно потребовать от вас больших усилий, так как принцип все еще остается тем же.

Как правильно умножать двузначные числа? Для этого недостаточно просто прочитать или выучить приведенную инструкцию. Помните, для того чтобы освоить принцип, как умножать двузначные числа, в первую очередь нужно постоянно практиковаться – решать как можно больше примеров, как можно реже пользоваться калькулятором.

Как умножать в уме

Научившись блестяще умножать на бумаге, можно задаться вопросом, как быстро умножить двузначные числа в уме.

Конечно, это не самая простая задача. Она требует некоторой концентрации, хорошей памяти, а также способности удерживать в голове некоторое количество информации. Однако и этому можно научиться, приложив достаточно усилий, тем более если подобрать правильный алгоритм. Очевидно, что легче всего умножать на круглые числа, поэтому самым простым способом является разложение чисел на множители.

Некоторые хитрости при умножении двузначных чисел

Но существует ли более легкий способ в уме умножать двузначные числа, и как это сделать?

Есть несколько хитростей. Они помогут вам легко и быстро умножать двузначные числа.

Ставим 7 в середину, 374. Это и есть ответ.

Если при сложении получается число больше 10, то следует просто добавить единицу к первому числу. Например, 79 × 11.

14 = 2 × 7, поэтому при выполнении математических операций можно умножить сначала на 7, а потом на 2.

Например, чтобы умножить число на 29, можно сначала умножить его на 30, а потом отнять от полученного числа данное число один раз. Это правило справедливо для любых десятков.

Источник

Быстрый способ умножения двузначных чисел

Ну а ничего, что такой способ годится только для вариантов, когда одно из чисел от 90 до 99. Иначе :

Запоминать способ для вариантов, где один из множителей в диапазоне 10 чисел.. ну несерьезно, передай Кондрашеву А.А.

А я лет с 11-13 научилась умножать в уме числа 3х, 4х значные, 5тизначные на 2хзначные, например. Я просто в уме вижу перед собой листок и решаю на нем пример, элементарное умножение в столбик.
Конечно, эту процедуру можно и на листочке производить, но листочек память не тренирует)))

А двухзначные раскладываю на близкие круглые числа, потом прибавляю или отнимаю недостающие единицы

Нечётные чуть длиннее, например 79*95
5*9=45
5*70=350
+45=395
90*9=810
90*70=6300
+810=7110
+395=7505

Способ универсальный, от простого к сложному, подходит и для многозначных в любых комбинациях, ограничение только по количеству цифр, которое может запомнить мозг.

Была статья на хабре)
Там гораздо круче, несколько способов.

И этот, в том числе, был

По мне так проще всего так:
95*88=

1. 95*8=720+40=760
2. 760*10=7600 (конечно только в случаях 88 99 33 66)
3. 7600+760=8360

Это шутка?

Почему ЭТО работает

Несколько лет назад по интернету гуляла интригующая картинка

Многие уже успели проверить это для разных пар чисел. Сегодня я хочу показать, почему это работает для любых чисел, близких к сотне. И, что самое забавное, не только для них.

Не будем забивать пост картинками и шутками, а сразу перейдем к делу.

Допустим, у нас есть два числа, которые мы хотим перемножить. Назовем их a и b. Тогда, по вышеуказанному способу нам нужно отнять эти числа от 100 (получим 100-а и 100-b), вычесть их сумму из 100 и умножить результат на 100, получив таким образом разряд сотен. Чтобы получить разряд единиц, числа 100-a и 100-b нужно перемножить. Сложив сотни и единицы, получим предполагаемый результат умножения. Запишем это формально:

Раскроем еще одни скобки:

В итоге, раскрывая до конца:

Получаем верное тождество, выполняющееся для любых чисел

Интересно, что при доказательстве не использовалось, что a и b должны быть меньше 100. Давайте перемножим этим способом, скажем, 456 и 789:

Умножим на 100, получим 114500. Это «как бы» разряд сотен, хотя тут есть уже и тысячи и десятки тысяч и т.д.

Сложим эти числа, получим

245284 + 114500 = 359784

Перемножив числа 456 и 789 на калькуляторе или в столбик, получим такой же результат.

Спасибо за внимание)

Четыре недели

Так вышло, что срочно понадобилось снять квартиру на месяц, сдавать никто не хотел на такой короткий срок и пришлось искать посуточную.

Диалог с одной владелицей квартиры:

— 1100, у Вас не выйдет 4 недели.

— Как не выйдет? 29 дней.

— Ну это же не четыре недели!

— В неделе сколько дней?

— Ой, знаете, сейчас у меня календаря рядом нет, смотреть Вам еще тут.

*перезванивает через полчаса*

— Знаете, я тут проверила, и правда если 29 дней, то 4 недели выходит. Давайте по 1000

Как крупье считают ставку

Один из важнейших навыков крупье это в считанные секунды посчитать сколько выиграл победный номер.

Опытный крупье считает эту ставку быстрее чем вы это сделаете на калькуляторе.

Каждый чипс дает определенные выигрыши, например если поставить на линию между 11 и 12, это означает что вы покрываете сразу два числа и если выпадет 11 или 12 то вам заплатят 17 к 1.

Чем больше чипс покрывает номеров, том меньше коэффициент.

1 номер называют Страйт ап = 35 к 1
2 номера сплит = 17
3 номера стрит = 11
4 номера корнер = 8
6 номеров сикс лайн = 5

И вот на картинке у нас: (11 номер выпал)
3 раза по 35
3 раза по 17
2 раза по 8
4 раза по 5
3 раза по 11

Такой вот пример, и считать такую ставку нужно очень быстро, секунд за 5-15

(На фото сделан сетофф в разные стороны просто что бы было видно)

Вот еще фото, посчитайте сами и пишите в комменты что получилось без помощи калькулятора)) если вы посчитали в уме хотя бы за 45 секунд то скорее всего вы либо крупье, либо математик)

Чаевые математика

Турция и математика.

У среднестатистического жителя Турции математика вызывает благоговейный страх. Обычно это самый сложный предмет в школе.

Маленькая история как я прослыла звездой математики среди подружек.

Минут 15 я потратила на то, чтобы объяснить «аудитории», что старый автобус может вообще сломаться на обочине, если ему приспичило, а скорость нового автобуса от этого никак не зависит. Чувствую, что до конца не убедила.

Быстрый устный счет

В общем, думаю любому может пригодиться пара секретиков быстрого счета. К сути.

Возвести в квадрат

Итак, нам дано число, например, 97. Требуется возвести его в квадрат.

Найдем ближайшее круглое число А = 100

Оно на 3 больше исходного, значит B будет на 3 меньше исходного. Остается перемножить A*B и прибавить 3^2, получив 100 * 94 + 3^2 = 9409.

Очевидно, это работает на любых числах: возведем в квадрат число 2018. Итак, думаю самый простой способ взять d=18, тогда получится (2018-18)(2018+18) + 18^2 = 2000 * 2036 + 18^2 = 4072000 + 18^2 = 4 072 324.

(хотя кто-то предпочтет знать отдельный метод для двузначных чисел, но я посчитал, что это частный случай, и пикабушникам это просто не нужно. Кстати, сколько будет 49.5^2?)

Перемножить два числа

Здесь довольно много способов.

3) Всегда остается старый, добрый способ посчитать поразрядно. То есть:

Целая часть корня числа

Итак, начинаем совсем грубо.

2) 100 ^ 2 = 10000 >> 2018.

3) Ок, пусть будет 50.

4) 50^2 = 2500 > 2018 (чегООО? Опять мимо?)

4) 1 500 000^2 = 1.5 ^ 2 * 1 000 000 ^ 2 = 2 250 000 000 000 F

6) 1 550 000^2 = 155^2 * 10^4^2 = (200 * 110 + 45^2) * 10^8 = (200 * 110 + 2025) * 10^8 = (22 000 + 2025) * 10^8 = 24 025 * 10^8 = 2 402 500 000 000 > F

Годный лайфхак:

Не дайте себя обмануть в магазине. Устный счёт для чайников и «гуманитариев».

Преподавая технические дисциплины, сталкиваюсь с тем, что у детей зачастую не возникает проблем при сложении чисел. А вот при вычитании долго думают и гораздо чаще ошибаются.

Думаю, такая же история знакома и взрослым.

Ну а раз уж складывать гораздо проще, чем вычитать, то обычно предлагаю детям и своим знакомым использовать такую фишку, как вычитать с помощью сложения.

Обычно дети схватывают моментально и начинают гораздо быстрее считать в уме и реже ошибаются.

если это 164-32, то обычно проблем не возникает, ведь у первого числа и число десятков и единиц больше, чем у второго и ответ дать просто.

Но как только появляется необходимость вычесть 126-78, то это часто приводит к ошибкам. А если это ещё и дробные числа, то совсем плохо.

Эта ситуация знакома и взрослым по необходимости быстро посчитать, сколько должен дать сдачи продавец.

Так в чем же фишка, и как использовать сложение при необходимости вычитания?

Между вычитаемыми числами нужно найти какое-нибудь круглое число. И чем «круглее», тем будет проще.

Вернёмся к примеру, 126-78. Какое круглое число находится между этими числами? Правильно, 100.

А теперь считаем, сколько нужно прибавить к 100, чтобы получить первое число? 26. А сколько нужно прибавить ко второму числу, чтобы получить 100? 22. Значит, наш ответ 26+22=48.

И второй пример выше:

Сколько нужно прибавить к 200, чтоб получить 435.3? 235.3.

Сколько нужно прибавить к 178.7, чтобы получить 200? 21.3.

Все знакомые, которых научил такому способу, говорят, что теперь у них не возникает проблем в магазинах, когда считают сдачу.

Источник