Как уменьшить погрешность измерений
Порядок уменьшения погрешности измерений
Уменьшение погрешности измерений, а следовательно и повышение точности измерений, сводится к исключению грубых и систематическихпогрешностей и снижению влияния случайных погрешностей и неисключенных остатков систематических погрешностей.
Сначала, при обработке экспериментальных данных, стремятся исключить грубые погрешности.
При выполнении многократних наблюдений трудно сделать вывод, обусловленные полученные экстремальные значения измеряемой величины (наибольшие и наименьшие) являються грубыми ошибками, или они являются результатом случайного разброса измеряемого значения.В этом случае используют метод математической статистики, основанный на втором свойству случайных погрешностей. Вычисляют интервал, в котором все значения наблюдений должны находиться с высокой степенью вероятности, и если некоторые из экспериментальных данных выходят за него, то они считаются грубыми ошибками, которые не учитываются при получении результата измерений.
Выявление, оценка и устранение известных систематических погрешностей из результата измерений является важной задачей. Систематическую погрешность выявляют путем анализа условий и методов измерений,а устраняют следующим образом:
Прежде всего пытаются исключить источники погрешностей до начала измерений путем выявления и устранения причин их возникновения. Например, систематическую составляющую дополнительной погрешности ЗО уменьшают ужесточением требований к условиям измерений (ограничением диапазона температур, давлений и т.п.).
Результаты, в которых исключены систематические погрешности, называются исправленными. Обычно стараются исключить систематические погрешности из результата наблюдений, но если они имеют постоянное значение, их нельзя исключать из результата измерений.
Если обозначенными способами исключить систематическую погрешность не удается, ее пытаются исключить экспериментально, то есть путем надлежащей организации и проведения измерений, что обычно приводит к значительному повышению трудоемкости выполнения измерений.Для этого используются методы:
· Метод замещения является наиболее универсальным методом. Измерения выполняются в два этапа. Сначала с прибором делают отсчет измеряемой величины, после этого вместо измеряемой величины на вход прибора подают известную величину, значение которой с помощью регулируемой меры устанавливают таким образом, чтобы показания прибора были как и при включении измеряемой величины.За результат измерения принимают значение меры.
· Метод компенсации погрешностей по знаку: два измерения выполняются так, чтобы постоянная систематическая погрешность входила в результаты измерений с разными знаками. После этого берется среднее арифметическое двух измерений.
· Метод симметричных наблюдений: заключается в проведении многократных наблюдений через равные промежутки времени и усреднении результатов наблюдений, симметрично расположенных относительно среднего наблюдения. Этот метод используют для устранения погрешностей через влияющие величины, которые изменяются по периодическому закону.
Случайные погрешности полностью исключить невозможно. Поэтому на практике стараются снизить их влияние на результат измерения: увеличивают количество наблюдений n, поскольку случайная погрешность обратно пропорціональна 
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Погрешности измерения и методы их уменьшения?
Конспект лекций
«метрология, стандартизация и сертификация»
МЕТРОЛОГИЯ
Определение метрологии, ее виды и основная функция?
Основные функции метрологии:
— создание общей теории измерений;
— образование единиц физических величин и систем единиц;
— разработка методов и средств измерений, методов определения точности, основ обеспечения единства и единообразия средств измерений;
— создание эталонов и образцовых средств, проверке мер и средств измерений.
Важнейшей задачей метрологии является обеспечение единства измерений,
Единство измерений—состояние измерений, характеризующееся тем, что их результаты выражаются в узаконенных единицах, размеры которых в установленных пределах равны размерам единиц, воспроизводимых первичными эталонами, а погрешности результатов измерений известны и с заданной вероятностью не выходят за установленные пределы.
Единство измерений достигается путем точного воспроизведения и хранения в специализированных организациях установленных единиц физических величин и передачи их размеров применяемым на практике СИ. Воспроизведение единицы физической величины осуществляется в результате операций по материализации единицы физической величины с помощью государственного эталона.
Передача размера единицы — приведение размера единицы физической величины, хранимой поверяемым средством измерений, к размеру единицы, воспроизводимой или хранимой эталоном, осуществляемое при их поверке (калибровке). Размер единицы передается от более точных средств измерений к менее точным.
Хранение единицы — совокупность операций, обеспечивающих неизменность во времени размера единицы, присущего данному средству измерений.
Определение измерения?
Измерение физической величины—совокупность операций по применению технического средства, хранящего единицу физической величины, обеспечивающих нахождение соотношения (в явном или неявном виде) измеряемой величины с ее единицей и получение значения этой величины.
Измерительная задача — задача определения значения физической величины путем ее измерения с требуемой точностью в заданных условиях измерений.
Объект измерения — тело (физическая система, процесс, явление и т.д.), которое характеризуется одной или несколькими измеряемыми физическими величинами.
§ Вал, у которого измеряют диаметр;
§ технологический процесс, во время которого измеряют температуру;
§ Положение корабля, координаты которого измеряют.
Область измерений — совокупность измерений физических величин, свойственных какой-либо области науки или техники и выделяющихся своей спецификой.
Примечание: Выделяют ряд областей измерений: механические, магнитные, акустические, измерения ионизирующих излучений и др.
Вид измерений — часть области измерений, имеющая свои особенности и отличающаяся однородностью измеряемых величин.
Пример:В области акустических измерений могут быть выделены как виды измерений: измерения амплитуды, частоты, фазы, акустического давления и др.
Принцип измерений — физическое явление или эффект, положенное в основу измерений.
1. Применение явления термо-ЭДС для измерения температуры.
2. Применение явления упругости материала для измерения его твёрдости.
3. Применение эффекта Допплера для измерения скорости.
4. Использование силы тяжести при измерении массы взвешиванием.
Метод измерений — прием или совокупность приемов сравнения измеряемой физической величины с ее единицей в соответствии с реализованным принципом измерений.
Методика выполнения измерений (МВИ) — установленная совокупность операций и правил при измерении, выполнение которых обеспечивает получение результатов измерений с гарантированной точностью в соответствии с принятым методом.
Погрешности измерения и методы их уменьшения?
Точность результата измерений—одна изхарактеристик качества измерения, отражающая близость к нулю погрешности результата измерения.
Примечание: Точность измерений тем или иным средством измерений (СИ) определяется их погрешностью. Высокая точность измерений соответствует малым погрешностям как систематическим, так и случайным.
Погрешность результата измерений—отклонение результата измерения от истинного (действительного) значения измеряемой величины.
· Погрешность не следует путать с ошибкой измерений, связанной с субъективными обстоятельствами.
Абсолютная погрешность измерения—погрешность измерения, выраженная в единицах измеряемой величины.
Относительная погрешность измерения—погрешность измерения, выраженная отношением абсолютной погрешности измерения к действительному или измеренному значению измеряемой величины.
Вагон массой 50000 кг измерен с абсолютной погрешностью ±50 кг, при этом относительная погрешность составляет: ±50/50000 = ±0,1%.
Примечание: Относительную погрешность в долях или процентах находят из отношений:
где Dх — абсолютная погрешность измерений;
х — действительное или измеренное значение величины.
Систематическая погрешность — постоянная, или изменяющаяся по определенному закону при повторных измерениях одной и той же величины погрешность. Она может быть связана, например, с ошибкой в градуировке шкалы.
Постоянные погрешности—погрешности, которые длительное время сохраняют свое значение, например, в течение времени выполнения всего ряда измерений.
Периодические погрешности—погрешности, значение которых является периодической функцией времени или перемещения указателя измерительного прибора.
Случайная погрешность измерения—составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных с одинаковой тщательностью, одной и той же физической величины.
В отличие от систематической ее нельзя исключить из результатов измерений, однако ее значение может быть уменьшено в результате специальных способов обработки результатов измерений, основанных на положениях теории вероятности и математической статистики.
Промах — погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда.
Примечание: Иногда вместо термина «промах» применяют термин грубая погрешность измерений
Общим методом уменьшения погрешностей является конструктивно- технологический метод, основанный на выявлении и устранении причин и источников возникновения погрешностей.
Примерами использования такого метода являются: термостатирование прибора (для исключения температурной погрешности), применение экранов и фильтров (для уменьшения погрешностей от влияния электромагнитных полей, наводок и др.), рациональное расположение средств измерений по отношению друг к другу, к источнику влияющих воздействий и к объекту исследования (например, магнитоэлектрические приборы должны быть удалены друг от друга) и др.
Во многих случаях использование данного метода для достижения требуемой точности измерения встречает большие затруднения и может привести к резкому возрастанию стоимости средств измерений.
Более широкое применение получили методы структурной и (или) временной избыточности, т.е. на введении дополнительных средств измерений (измерительных преобразователей, приборов и др.) и (или) выполнении дополнительных измерений, результаты которых обрабатываются по определенному алгоритму.
Уменьшение погрешности измерений
Методы исключения систематических погрешностей: Постоянные сист. погр. обнаруживают только путём сравнения результатов измерений с другими, полученными с использованием более точных методов и средств измерения.
Систематическая погрешность (∆с) проявляется в виде смещения Хизм относительно Х. Может быть учтена введением поправки.
Метод введения поправок позволяет достаточно просто вычислить и исключить из результата изм-я сист погр-сти. Поправка С – величина одноимённая с измеряемой Хи, которая вводиться в результат измерения Х=Хи+∆с+С с целью исключения (компенсации) сист погр.
При ∆с ≈ 0 – измерения называются правильные.
Метод замещения обеспечивает наиболее полную компенчацию пост. Сист. Погр. Его суть состоит в такой замене замеряемой величины Хи известной величиной А, получаемой с помощью регулируемой меры, чтобы показание измерительного прибора сохранилось неизменным. Значение измеряемой вел. считывают по указателю меры. При использовании метода погрешность неточного измерительного прибора устраняют, а погрешность измерения определяют только погрешностью самой меры и погрешностью отсчёта измеряемой величины по указателю меры.
· повышение класса точности прибора;
Случайная погрешность проявляется в виде разброса значений Хизм относительно Х. Может быть оценена в виде доверительного интервала.
Способы уменьшения 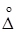
· повышение класса точности измерительных приборов (при однократных измерениях);
· проведение многократных наблюдений с помощью высокочувствительных приборов.
Понятие Классы точности средств измерений включает обобщенную характеристику средства измерения, определяемую пределами основной и дополнительной допускаемых погрешностей, т.е. обеспечивающую гарантированные границы этих погрешностей.
Применимость класса точности в качестве оценки точности средства измерения ограничена, так как при этом нет возможности раздельного нормирования случайных и систематических погрешностей, влияний внешних условий, динамических погрешностей.
Классы точности присваиваются средствам измерения на стадии их разработки и пересматриваются в процессе эксплуатации путем нормирования предельных допускаемых погрешностей при периодических поверках (ГОСТ 8.401-80).
Пределы допускаемой абсолютной погрешности выражаются в виде
Пределы допускаемой относительной погрешности рассчитываются из значения абсолютной погрешности D, измеряемой величины X, наибольшего по модулю значения шкалы Хк по соотношениям
Предел допускаемой приведенной основной погрешности определяют по абсолютной погрешности D и нормирующему значению L по выражению
В соответствии с основной метрологической характеристикой СИ – погрешностью ИП присваивают класс точности.
В зависимости от применяемого способа назначения класса точности применяется соответствующая форма их обозначения. Погрешность может нормироваться, в частности, по отношению к:
Для стрелочных приборов принято указывать класс точности, записываемый в виде числа, например, 0,05 или 4,0. Это число дает максимально возможную погрешность прибора, выраженную в процентах от наибольшего значения величины, измеряемой в данном диапазоне работы прибора. Так, для вольтметра, работающего в диапазоне измерений 0 — 30 В, класс точности 1,0 определяет, что указанная погрешность при положении стрелки в любом месте шкалы не превышает 0,3 В.
Относительная погрешность результата, полученного с помощью указанного вольтметра, зависит от значения измеряемого напряжения, становясь недопустимо высокой для малых напряжений. При измерении напряжения 0,5 В погрешность составит 20 %. Как следствие, такой прибор не годится для исследования процессов, в которых напряжение меняется на 0,1 — 0,5 В.
Обычно цена наименьшего деления шкалы стрелочного прибора согласована с погрешностью самого прибора. Если класс точности используемого прибора неизвестен, за погрешность s прибора всегда принимают половину цены его наименьшего деления. Понятно, что при считывании показаний со шкалы нецелесообразно стараться определить доли деления, так как результат измерения от этого не станет точнее.
Обозначения класса точности могут иметь вид заглавных букв латинского алфавита, римских цифр и арабских цифр с добавлением условных знаков.
Если класс точности обозначается латинскими буквами, то класс точности определяется пределами абсолютной погрешности.
Если класс точности обозначается арабскими цифрами без условных знаков, то класс точности определяется пределами приведённой погрешности и в качестве нормирующего значения используется наибольший по модулю из пределов измерений.
Если класс точности обозначается арабскими цифрами с галочкой, то класс точности определяется пределами приведённой погрешности, но в качестве нормирующего значения используется длина шкалы.
Если класс точности обозначается римскими цифрами, то класс точности определяется пределами относительной погрешности.
Расшифровка обозначений классов точности на средствах измерений
Поверка средств измерения
В основе обеспечения единообразия средств измерений лежит система передачи размера единицы измеряемой величины. Технической формой надзора за единообразием средств измерений является государственная (ведомственная) поверка средств измерений, устанавливающая их метрологическую исправность.
Пригодным к применению в течение определенного межповерочного интервала времени признают те СИ, поверка которых подтверждает их соответствие метрологическим и техническим требованиям к данному СИ.
Средства измерений подвергают первичной, периодической, внеочередной, инспекционной и экспертной поверкам.
Первичной поверке подвергаются СИ при выпуске из производства или ремонта, а также СИ, поступающие по импорту.
Периодической поверке подлежат СИ, находящиеся в эксплуатации или на хранении через определенные межповерочные интервалы, установленные с расчетом обеспечения пригодности к применению СИ на период между поверками.
Инспекционную поверку производят для выявления пригодности к применению СИ при осуществлении госнадзора и ведомственного метрологического контроля за состоянием и применением СИ.
Экспертную поверку выполняют при возникновении спорных вопросов по метрологическим характеристикам (MX), исправности СИ и пригодности их к применению.
Достоверная передача размера единиц во всех звеньях метрологической цепи от эталонов или от исходного образцового средства измерений к рабочим средствам измерений производится в определенном порядке, приведенном в поверочных схемах.
Поверочная схема – это утвержденный в установленном порядке документ, регламентирующий средства, методы и точность передачи размера единицы физической величины от государственного эталона или исходного образцового средства измерений рабочим средствам.
Различают государственные, ведомственные и локальные поверочные схемы органов государственной или ведомственных метрологических служб.
Поверке подвергаются СИ, выпускаемые из производства и ремонта, получаемые из-за рубежа, а также находящиеся в эксплуатации и хранении. Основные требования к организации и порядку проведения поверки СИ установлены ГОСТ 8.513-84.
Основополагающие документы по обеспечению единства измерений
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
ЛЕКЦИЯ 6. §5. Методы уменьшения погрешностей измерений
§5. Методы уменьшения погрешностей измерений.
Общим методом, пригодным в принципе для уменьшения погрешностей, является конструктивно-технологический метод, основанный на выявлении причин и источников наиболее существенных погрешностей и всемерном снижении их влияния. В конструктивно технологическом методе используются такие приемы, как термостатирование, применение малошумящих электронных компонентов, использование прецизионных элементов и узлов, материалов со стабильными характеристиками, рационального конструирования и совершенной технологии изготовления средств измерений. Однако возможности указанного метода весьма ограничены и что также очень важно, его применение с целью достижения высоких точностей измерений приводит к резкому возрастанию стоимости средств измерений. В связи с этим широкое распространение получили методы повышения точности, основанные на введении структурной и (или) временной избыточности, т. е. на введении дополнительных средств измерений (измерительных преобразователей, измерительных устройств) и (или) выполнении дополнительных измерений, результаты которых обрабатываются по специальному алгоритму, позволяющему повысить точность. Поведение систематических и случайных погрешностей во времени (при повторных измерениях) существенно различно, в связи с чем существенно отличаются и методы их уменьшения. При постоянстве значения измеряемой величины наиболее эффективным методом уменьшения случайной погрешности является усреднение результатов наблюдения. Среднее квадратическое отклонения погрешности результата измерения, т. е. среднего значения результатов n наблюдений, уменьшается до 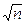
Гораздо труднее, уменьшить случайную погрешность в том случае, когда значение измеряемой величины изменяется во времени. В этом случае используется более сложная процедура фильтрации, целью которой является получение оптимальной оценки измеряемой величины, причем оценка также рассматривается как процесс, протекающий во времени. Погрешность оценки (разность между оценкой и измеряемым процессом) представляет собой функцию времени, а в качестве критерия оптимальности оценки используют некоторый функционал от погрешности оценки на временном интервале наблюдения, например средний квадрат погрешности.
В зависимости от вида используемых преобразований различают линейную и нелинейную фильтрацию, причем практическая реализация необходимых преобразовании может осуществляться как аппаратурным, так и программным способом.
Необходимо отметить, что для реализации оптимальной процедуры фильтрации необходима априорная информация о характеристиках изучаемого сигнала и помехи (случайной погрешности). Для более подробного изучения фильтрации следует обратиться к специальной литературе.
Рассмотрим основные методы уменьшения систематических погрешностей. Как известно, систематические погрешности делятся на постоянные и переменные. Наиболее распространенные методы исключения постоянных систематических погрешностей: введения поправок, замещения, компенсации погрешностей по знаку. Однако на практике, особенно при использовании информационно-измерительных систем для измерения неэлектрических величин в производственных условиях, доминирующую роль играют переменные систематические погрешности, вызванные изменениями температуры, влажности, давления окружающей среды, изменениями питающих напряжений, влиянием внешних электрических и магнитных полей и т. п. Следует отметить, что переменные систематические погрешности зависят от изменяющихся внешних воздействий, значения которых обычно не известны и поэтому проявляют себя как случайные функции времени. В это смысле от случайных погрешностей они отличаются тем, что представляют собой нестационарные случайные функции изменяющиеся во времени относительно медленно. Уменьшение подобных переменных систематических погрешностей представляет собой актуальную и достаточно сложную задачу.
Указанные выше методы исключения систематических погрешностей находят применение главным образом в лабораторной практике — их применение в автоматических измерительных устройствах и ИИС в производственных условиях и при изменениях систематических погрешностей в большинстве случаев невозможно. В связи с этим получили развитие методы уменьшения переменных систематических погрешностей, основанные на использовании структурной и (или) временной избыточности.
1). Конструктивно-технологические методы (экранирование, термостатирование, метод размещения элементов или узлов на растяжке, старение элементов, подбор контактных пар, теоретический расчет), 2). Поверка приборов. 3). Рандомизация или перевод систематических погрешностей в ряд случайных. 4). Метод инвертирования. 5). Метод замещения. 6). Использование отрицательной обратной связи (метод автокомпенсации). 7). Метод вспомогательных измерений. 8). Метод симметричных измерений. 9). Метод тестовых сигналов. 10). Метод образцовых сигналов. 11). Итерационный метод.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Практические приемы уменьшения погрешностей
Обычно выделяют три группы погрешностей: неустранимая погрешность; погрешность метода; вычислительная погрешность. Неустранимая погрешность порождается: а) неточностью входных данных в математическом описании задачи; б) несоответствия математической модели реальной задаче. Погрешность метода возникает из-за того, что используются приближенные методы. А погрешность вычислений возникает при вводе-выводе и при выполнении математических операций, а также при округлениях. Попробуем привести несколько практических приемов для уменьшения влияния вычислительной погрешности на результаты вычислений.
1. Сложение чисел необходимо проводить по мере их возрастания так как в машинной арифметике из-за погрешности округления существенен порядок выполнения операций.
2. В некоторых случаях имеет смысл выполнить предварительные преобразования вычисляемого выражения.
Например, вместо (a+b)^2 для случая, когда одно число намного меньше другого, лучше использовать выражение: a^2+2ab+b^2. Перемножение большого и маленького числа: 2ab позволит слегка поправить ситуацию.
3. Необходимо исключать вычитание двух почти равных чисел, тем более когда такая разность находится в знаменателе выражения.
4. Если числа равны a и b почти равны, то вычитание этих чисел следует производить раньше, чем деление или умножение.
К примеру, следует отдать предпочтение выражению (a-b)/c, а не выражению a/c-b/c. Во-первых здесь меньше операций (смотри пункт 3 и 6), а во-вторых, после деления числа станут меньше и еще меньше будут отличаться друг от друга, что может привести к обращению разности в ноль.
5. При перемножении нескольких чисел надо сразу перемножать самое большое число и самое маленькое, так как умножение друг на друга нескольких маленьких чисел может привести к появлению машинного нуля.
6. Всегда следует стремиться к уменьшению числа арифметических операций. Это объясняется тем, что чем больше операций, тем больше суммирующие погрешности.
