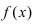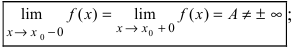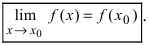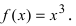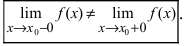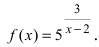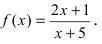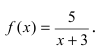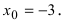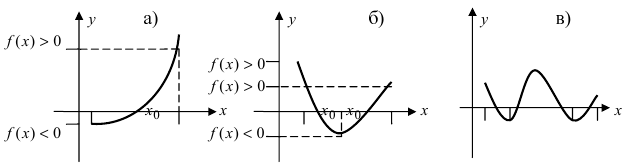Как указывать точки разрыва
Непрерывность функций и точки разрыва с примерами решения
Содержание:
Непрерывность функций и точки разрыва
Непрерывность функции
Определение: Функция
— предел функции в точке 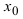
Пример:
Найти область непрерывности функции
Решение:
Данная функция непрерывна 
Замечание: Всякая элементарная функция непрерывна в области своего определения.
Точки разрыва
Определение: Точки, в которых не выполняется хотя бы одно из условий непрерывности функции, называются точками разрыва. Различают точки разрыва первого и второго родов.
Определение: Точкой разрыва I рода называется точка, в которой нарушается условие равенства лево- и правостороннего пределов, т.е.
Пример:
Доказать, что функция 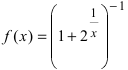
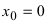
Решение:
Нарисуем график функции в окрестности нуля (Рис. 64): 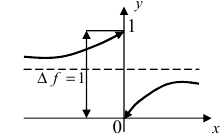
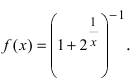
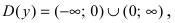
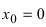
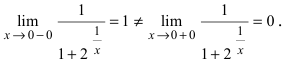
Замечание: По поводу точки разрыва I рода иначе говорят, что в этой точке функция испытывает конечный скачок (на Рис. 64 скачок равен 1).
Определение: Точка, подозрительная на разрыв, называется точкой устранимого разрыва, если в этой точке левосторонний предел равен правостороннему.
Пример:
Доказать, что функция 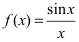
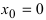
Решение:
В точке 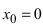
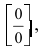
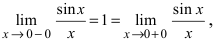
Определение: Все остальные точки разрыва называются точками разрыва II рода.
Замечание: Для точек разрыва второго рода характерен тот факт, что хотя бы
один из односторонних пределов равен 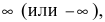
Пример:
Исследовать на непрерывность функцию
Решение:
Найдем область определения этой функции: 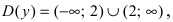
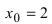
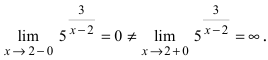
Пример:
Исследовать на непрерывность функцию
Решение:
Найдем область определения этой функции: 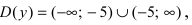
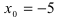
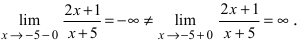
Операции над непрерывными функциями
Теорема: Сумма (разность) непрерывных функций есть непрерывная функция.
Доказательство: Докажем приведенную теорему для суммы двух функций 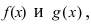
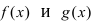
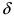
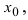
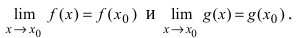
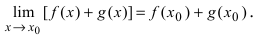
Теорема: Произведение непрерывных функций есть непрерывная функция.
Теорема: Частное двух непрерывных функций 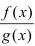
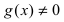
Теорема: Сложная функция от непрерывных функций есть непрерывная функция.
Схема исследования функции на непрерывность
Исследование функции на непрерывность проводят по следующей схеме:
Пример:
Исследовать на непрерывность функцию
Решение:
Согласно схеме исследования функции на непрерывность имеем:
Рис. 65. Поведение графика функции 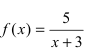
Из рисунка видно, что график функции 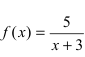
Свойства непрерывных функций на отрезке (a; b)
Свойства непрерывных функций на отрезке 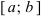
Определение: Замкнутый интервал 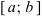
Приведем без доказательства свойства непрерывных функций на сегменте 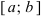
Теорема: Если функция 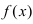
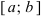
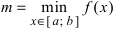
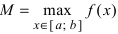
Пример:
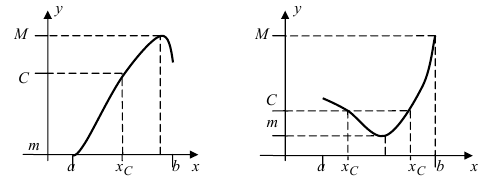
Привести примеры графиков функций, удовлетворяющих условиям теорем(см. Рис. 66).
Рис. 66. Графики функций, удовлетворяющих условиям теоремы.
Решение:
На графике а) функция достигает своего наименьшего 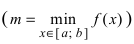
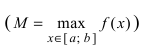
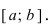
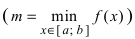
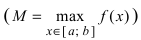
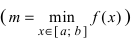
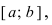
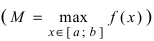
Тб. Если функция 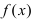
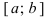
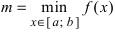
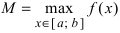
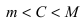
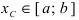
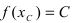
Пример:
Изобразить графики функций, удовлетворяющих условиям Тб (см. Рис. 67).
Рис. 67. Графики функций, удовлетворяющих условиям Тб.
Теорема: Если функция 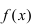
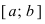
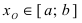
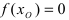
Пример:
Изобразить графики функций, удовлетворяющих условиям теоремы(см. Рис. 68).
Рис. 68. Графики функций, удовлетворяющих условиям теоремы.
На графике а) существует единственная точка, в которой выполняются условия теоремы. На графиках б) и в) таких точек две и четыре, соответственно. Однако в случаях б) и в) для удовлетворения условий теоремы надо разбивать сегмент на отдельные отрезки.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Точки разрыва функции — алгоритмы и примеры решения
Нахождение точек разрыва функции является одним из важнейших элементов исследования в математическом анализе. Многие студенты используют для пополнения своих знаний информацию из интернета, однако даже не подозревают, что она может быть недостоверной. Чтобы избежать неприятных последствий, следует решать по методике, которую рекомендуют специалисты, а также обладать определенными базовыми знаниям.
Общие сведения
Когда математики говорят, что нужно произвести исследование функции на непрерывность, т. е. необходимо найти точки разрыва первого и второго рода. Если же таковых нет, то данное утверждение следует доказать математическим методом.
Непрерывной называется функция, которая не имеет точек разрыва, и меняется без существенных скачков в некоторых точках или промежутках, т. е. обладает определенным знакопостоянством. Это свойство определяется при помощи метода, представляющего совокупность математических преобразований. Последние основываются на теоремах. Они позволяют доказать существование или отсутствие точек и интервалов разрыва графика функции.
Базовые знания
Базовые знания — совокупность навыков, необходимых для решения какой-либо задачи. Для нахождения точек разрыва необходимы такие знания:
Когда список сформирован, тогда необходимо приступать к изучению материала. После полного понимания первого пункта необходимо переходить к последующему. Все пять элементов связаны между собой. Специалисты рекомендуют не заучивать наизусть понятия и термины, а понимать их.
Область определения
Областью определения некоторой функции w = f (p) называется интервал или числовой промежуток всех значений аргумента «р», при которых существует эта функция. Величину следует обозначать литерой «D». Конечная запись для вышеописанного тождества имеет такой вид: D (w) или D (f (р)).
Следует отметить, что D (w) зависит от ее вида. В алгебре бывают только простые и составные. К первым нужно отнести следующие подтипы:
К рациональным равенствам целого типа относятся любые выражения без корней, степеней, дробей, логарифмов, а также тождества, не содержащие каких-либо тригонометрических функций. В этом случае D соответствует всему интервалу действительных, которые обозначаются литерой «Z».
Для дробных D (w) зависит от знаменателя. В этом случае нужно решить уравнение, приравняв знаменатель к нулю. Например, чтобы найти D у функции вида w = [(p — 2)(p + 7)] / (p 2 — 1), нужно приравнять знаменатель дроби к 0.
Когда выражение является иррациональным, тогда нужно обратить внимание на степень корня и подкоренное выражение. Если степень четная, то выражение не должно быть отрицательным числом. Функция действительна для всех Z, кроме тех, которые превращают выражение под корнем в пустое множество. Например, для w = (p — 2) / [(p 2 — 1)]^(½) нужно решить неравенство (p 2 — 1) > 0. Интервалы, которым соответствует решение, можно записать в таком виде: (-бесконечность;-1) U (1;бесконечность). Бесконечность можно еще обозначать «inf».
Выражение под натуральным логарифмом должно быть всегда больше 0. В этом случае решается также неравенство, состоящее из тождества, находящегося под его знаком. Интервал для косинуса и синуса — все Z. Однако для tg (x) рекомендуется исключить значения аргумента (Pi / 2) + Pi * k, а для и ctg (x) — Pi * k (к принадлежит множеству Z).
Решение уравнений
Уравнения бывают нескольких видов: линейными, квадратными, кубическими и биквадратными. Первые являются самыми простыми, и решаются при помощи такой методики:
К квадратным относятся равенства вида ap 2 + bp + c = 0. Математики их классифицируют на неполные и полные. К первым относятся только равенства, которые не содержат второй или третий член. Квадрат при первом коэффициенте должен быть всегда. Существует 4 метода решения:
Рассчитать D по формуле: D = b 2 — 4ac.
Нахождение предела функции — основа математического анализа. В некоторых источниках описаны разнообразные формулы и теоремы. Предел состоит из трех элементов:
Виды разрывов
Чтобы исследовать функцию на непрерывность, нужно уметь определять характер разрыва. Он классифицируется следующим образом: первого и второго рода. Первые бывают двух типов: устранимые и неустранимые.
Разрыв I рода существует в том случае, когда оба предела (левосторонний и правосторонний) являются конечными, т. е. не равны inf. Когда оба предела равны, то это точка устранимого разрыва. В противном случае (при неравенстве односторонних пределов) — разрыв является неустранимым, и называется «скачком».
Решения задач
После получения базовых знаний необходимо разобрать примеры решения. Точки разрыва функции следует искать по следующему алгоритму:
Однако для начала нужно найти область определения, которая играет важную роль в решении. Если она является множеством всех действительных чисел, то искать разрыв не имеет смысла. Он не существует. Если указанная функция содержит неизвестную, которая может превратить ее значение в неопределенность, то нужно вычислить правосторонний и левосторонний пределы (пункт 1). После этого их нужно сравнить, и сделать выводы о принадлежности точки к какому-нибудь виду.
Простые варианты
Нужно исследовать функцию w = (r 2 — 1) / (r — 2) на непрерывность или доказать, что она разрывная. Область определения D (w) = (-inf;2) U (2;+inf). Существует некоторый разрыв в точке r = 2. Для классификации его характера необходимо найти пределы:
Из полученных вычислений можно сделать вывод, что r = 2 является разрывом II рода. Это были простые задачи. Однако существуют более сложные, в которых нужно выполнять математические преобразования.
Сложное задание
Дано некоторое выражение: (2s 2 — 98) / (4s 2 — 8s — 16). Необходимо представить его в виде функции, и доказать существование типа разрыва в пространстве. Для доказательства нужно сначала решить уравнение в знаменателе:
Это свидетельствует о том, что разрыв есть. Далее нужно определить его характер по такому алгоритму:
Выполнять вычисления для двух точек необязательно, поскольку пределы будут равны и в этом случае. Следовательно, это устранимый разрыв I рода.
Таким образом, для нахождения разрывов необходимо знать некоторые особенности и методику, позволяющую правильно классифицировать их характер.
Непрерывность функции в точке, разрывы первого и второго рода
Процесс исследования функции на непрерывность неразрывно связан с навыком нахождения односторонних пределов функции. Поэтому, чтобы приступить к изучению материала данной статьи, желательно предварительно разобрать тему предела функции.
Непрерывность функции в точке
Данное определение позволяет вывести следствие: значение предела функции в точках непрерывности совпадает со значением функции в этих точках.
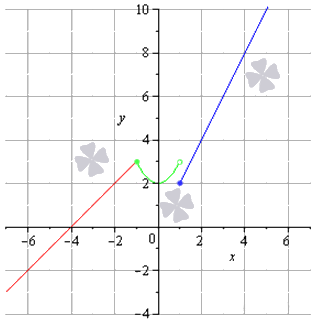
Решение
Соответствующая последовательность значений функций выглядит так:
на чертеже они обозначены зеленым цветом.
Соответствующая последовательность функций:
на рисунке обозначена синим цветом.
После вычисления значения функции в заданной точке очевидно выполнение равенства:
Устранимый разрыв первого рода
Решение
Ответ: пределы справа и слева являются равными, а заданная функция в точке х 0 = 5 не определена, т.е. в этой точке функция имеет устранимый разрыв первого рода.
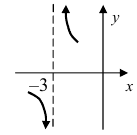
Неустранимый разрыв первого рода
Неустранимый разрыв первого рода также определяется точкой скачка функции.
Решение
Определим пределы справа и слева от этих точек и значение заданной функции в этих точках:
Ответ: в конечном счете мы получили:
Нам остается только подготовить чертеж данного задания.
Разрыв второго рода (бесконечный разрыв)
Решение
Зададим произвольную последовательность значений аргумента, сходящуюся к х 0 слева. К примеру:
Ей соответствует последовательность значений функции: