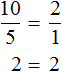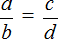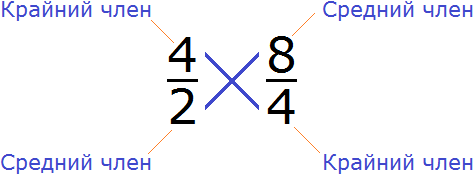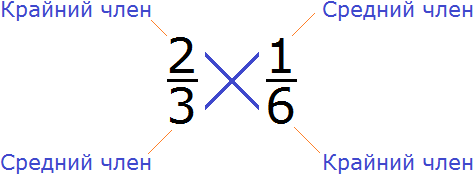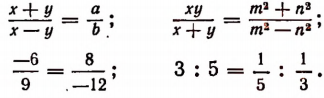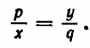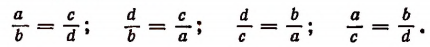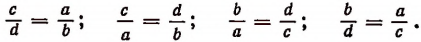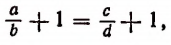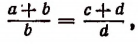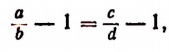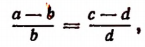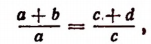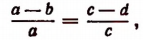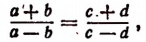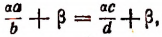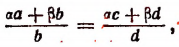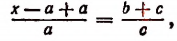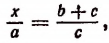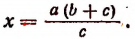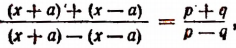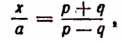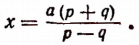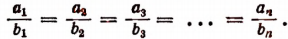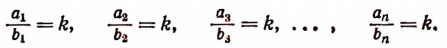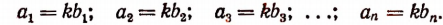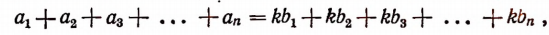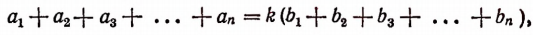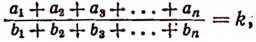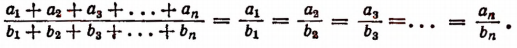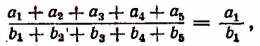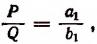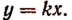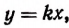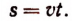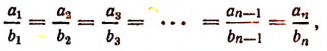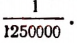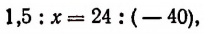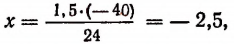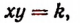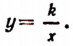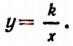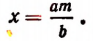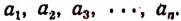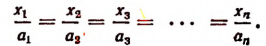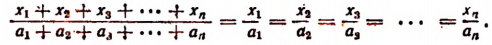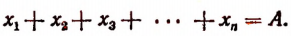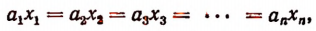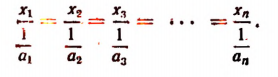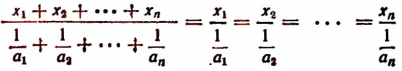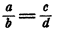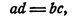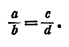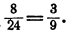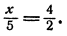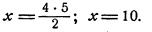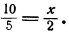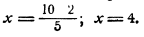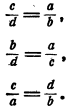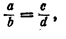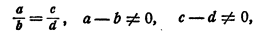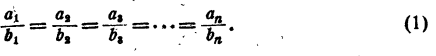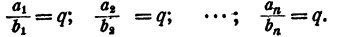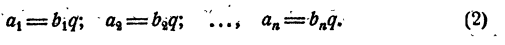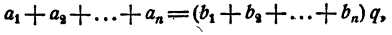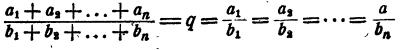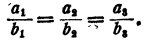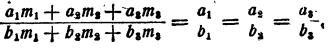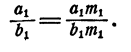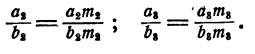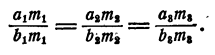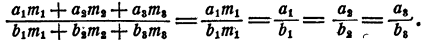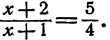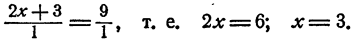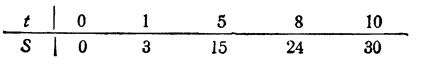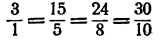Как указать верную пропорцию

Пропорция

Продолжаем изучать соотношения. В данном уроке мы познакомимся с пропорцией.

Что такое пропорция?

Пропорцией называют равенство двух отношений. Например, отношение равно отношению

Данная пропорция читается следующим образом:

Десять так относится к пяти, как два относится к одному

Дроби, из которых составлена пропорция, всегда равны. Например, если в пропорции 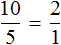выполнить деление в обеих дробях, то получится число 2 в обеих частях:

Предположим, что в классе 10 девочек и 5 мальчиков

Запишем отношение десяти девочек к пяти мальчикам:

Преобразуем данное отношение в дробь

Выполнив деление в этой дроби, мы получим 2. То есть десять девочек так будут относиться к пяти мальчикам, что на одного мальчика будет приходиться две девочки

Теперь рассмотрим другой класс в котором две девочки и один мальчик

Запишем отношение двух девочек к одному мальчику:

Преобразуем данное отношение в дробь:

Выполнив деление в этой дроби, мы снова получим 2. То есть две девочки так будут относиться к одному мальчику, что на этого одного мальчика будут приходиться две девочки:

В нашем примере десять девочек так относятся к пяти мальчикам, как и две девочки относятся к одному мальчику.

Пример 2. Рассмотрим отношение 12 девочек к 3 мальчикам

а также отношение 12 девочек к 2 мальчикам

Данные отношения не являются пропорциональными. Другими словами, мы не можем записать, что 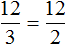, поскольку первое отношение, как видно на рисунке показывает, что на одного мальчика приходятся четыре девочки, а второе отношение показывает, что на одного мальчика приходятся шесть девочек.

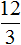
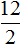
Поэтому отношение не пропорционально отношению .

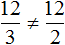
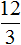
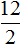
Вторая рассмотренная нами пропорция была . Мы пришли к выводу, что она составлена неправильно, поэтому поставили между дробями и знак не равно (≠). Если выполнить деление в этих дробях, получим числа 4 и 6. Понятно, что 4 не равно 6.

Можно проверить это, выполнив деление в этих дробях, то есть разделить 4 на 2, а 8 на 4. В результате с двух сторон получатся двойки. А 2 равно 2

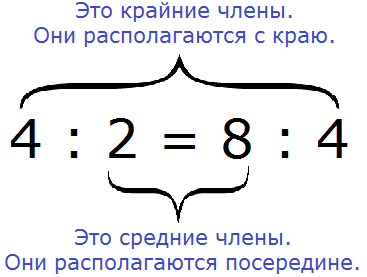
Все числа, находящиеся в пропорции (числители и знаменатели обеих дробей) называются членами пропорции. Эти члены подразделяются на два вида: крайние члены и средние члены.

В нашей пропорции 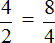крайние члены это 4 и 4, а средние члены это 2 и 8

Почему крайние члены называют крайними, а средние средними? Если записать пропорцию не в дробном, а в обычном виде, то сразу станет всё понятно:

Числа 4 и 4 располагаются с краю, поэтому их назвали крайними, а числа 2 и 8 располагаются посередине, поэтому их назвали средними:

С помощью переменных пропорцию можно записать так:

Данное выражение можно прочесть следующим образом:

a так относится к b, как c относится к d

Смысл данного предложения уже понятен. Речь идет о членах, участвующих в соотношении. a и d — это крайние члены пропорции, b и c — средние члены пропорции.

Основное свойство пропорции

Основное свойство пропорции выглядит следующим образом:

Произведение крайних членов пропорции равно произведению её средних членов.

Мы знаем, что произведение это ни что иное, как обычное умножение. Чтобы проверить правильно ли составлена пропорция, нужно перемножить её крайние и средние члены. Если произведение крайних членов будет равно произведению средних членов, то такая пропорция составлена правильно.

Например, проверим правильно ли составлена пропорция 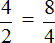. Для этого перемножим её крайние и средние члены. Легко заметить, что крайние и средние члены пропорции располагаются «крест-накрест», поэтому в умножении нет ничего сложного. Перемножаем члены пропорции «крест-накрест»:

4 × 4 = 16 — произведение крайних членов пропорции равно 16.

2 × 8 = 16 — произведение средних членов пропорции так же равно 16.

4 × 4 = 2 × 8

4 × 4 = 2 × 8 — произведение крайних членов равно произведению средних членов. Значит пропорция 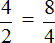составлена правильно.

Пример 2. Проверить правильно ли составлена пропорция

Проверим равно ли произведение крайних членов пропорции произведению её средних членов. Перемножим члены пропорции крест-накрест:

2 × 6 = 12 — произведение крайних членов пропорции равно 12

3 × 1 = 3 — произведение средних членов пропорции равно 3

2 × 6 ≠ 3 × 1 — произведение крайних членов пропорции НЕ равно произведению её средних членов. Значит пропорция 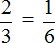составлена неправильно.

Поэтому в пропорции 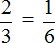разумнее заменить знак равенства (=) на знак не равно (≠)

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Источник

Составление и решение пропорций в математике

Пропорции — что это в математике

Валя съела 3 яблока из пяти. Какую часть яблок съела Валя?

Вначале узнаем, какую часть яблок составляет 1 яблоко. Всего у Вали было 5 яблок, значит, одно из них — это 1 5 часть всех яблок. Тогда 3 съеденных яблока составляют 3 5 всех яблок.

Тот же ответ получим, если 3 разделим на пять.

Получается, что 3 яблока соотносятся с пятью яблоками как 3 к 5.

Отношением двух чисел называют частное этих чисел.

Отношение показывает, во сколько раз одно число больше другого. Или какую часть первое число составляет от второго.

Термин «отношение» применяют в случаях, когда нужно выразить одну величину в долях другой. Например, одну площадь в долях другой площади. Это операцию выполняют с помощью деления.

Делимое в выражении отношения называют предыдущим членом. Делитель называют последующим членом.

В задаче 1 предыдущий член — это 3, последующий — 5.

Если есть два равных отношения, то они образуют пропорцию.

Пропорцией называют равенство двух отношений.

Даны два отношения: 3,8:2 и 5,7:3.

Можно ли составить из этих выражений пропорцию?

Найдем значения каждого из отношений:

Значения выражений оказались равными, значит, эти отношения равны.

Тогда можно записать равенство: 3,8:2=5,7:3.

Такое равенство называется пропорцией.

Ответ: да, можно составить из этих отношений чисел пропорцию.

Полученное равенство читают: «Отношение a к b равно отношению c к d» или «a относится к b, как c относится к d».

Числа a и d в пропорции называют крайними членами пропорции.

Числа b и c — средними членами пропорции.

Назовите крайние и средние члены пропорции 42:6=49:7.

Крайние члены пропорции — 42 и 7.

Средние члены пропорции — 6 и 49.

Средние члены пропорции — 5 и 35.

Понятие «пропорция» пришло из латинского языка. Слово в переводе означает соразмерность, определенное соотношение частей между собой.

Основное свойство пропорции, правило

Основное свойство пропорции

В верной пропорции произведение крайних членов равно произведению средних членов:

Определите, верна ли пропорция 6:2=9:3.

В верной пропорции произведение крайних членов равно произведению средних членов.

Значит, 6:2=9:3. Пропорция верна.

Обратное утверждение тоже верно:

Если произведение средних членов равно произведению крайних членов, то пропорция верна.

Если поменять в это пропорции местами средние члены, получим 60:10=12:2. Эта пропорция тоже верна. При перестановке произведение крайних и средних членов не изменилось.

Если в пропорции поменять крайние члены — 2:10=12:60, то произведение тоже не изменится.

Пропорция будет верной, если поменять местами средние члены или крайние члены.

Если какой-то из членов пропорции неизвестен, то его можно найти.

По основному свойству пропорции можно найти ее неизвестный член, если все остальные компоненты известны.

Найдите неизвестный член пропорции: 4,8:b=8:2,5.

Используем основное свойство пропорции: произведение крайних членов = произведению средних членов.

Составление и решение пропорций

Запишите пропорцию: 6 так относится к 18, как 9 относится к 27.

Слово «относится» заменяем на знак деления.

Получаем два отношения: 6:18 и 9:27.

Если эти два отношения равны, то получаем верную пропорцию.

Проверяем, верна ли пропорция.

Для этого воспользуемся основным свойством пропорции: произведение крайних членов = произведению средних членов.

Чтобы проверить, верна ли пропорция, воспользуемся основным свойством пропорции.

Запишем произведения крайних и средних членов пропорции:

Значит, произведение крайних членов равно произведению средних членов.

Вывод: пропорция верна.

Примеры уравнений с решением для 6 класса

Чтобы найти неизвестный член пропорции, используем основное свойство пропорции. Находим произведение крайних и средних членов. Выражаем неизвестный компонент.

Используем основное свойство пропорций. Записываем равенства произведений крайних и средних членов.

Решите уравнение: 0,25:x=3,75:3.

Но чтобы выражение осталось неизменным, нужно домножить на сто и делимое.

Чтобы найти неизвестный компонент пропорции, нужно воспользоваться основным свойством дроби.

По основному свойству дроби произведение крайних членов равно произведению средних членов.

Записываем полученное выражение:

1 действие — умножение.

Переводим смешанное число в неправильную дробь и умножаем на вторую: числитель на числитель, знаменатель на знаменатель.

Сокращаем дробь: есть одинаковые числа в числителе и знаменателе.

2 действие — деление.

Смешанное число переводим в неправильную дробь.

Умножаем 7 5 на взаимно обратную дробь.

Источник

Что такое пропорция

Что такое пропорция

Пропорция — это равенство двух отношения.

Пропорциональный — это такой, который находится в определенном отношении к какой-либо величине.

Пропорция всегда содержит равные коэффициенты.

Если выразить определение формулой, то выглядеть оно будет так:

a и d — крайние члены пропорции, b и с — средние члены пропорции.

Читается это выражение так: a так относится к b, как c относится к d

Например:

Это равенство двух отношений: 15 так относится к 5, как 9 относится к 3.

15 и 3 — крайние члены пропорции.

5 и 9 — средние члены пропорции.

Наглядный пример для понимания:

У нас есть восемь кусочков аппетитной пиццы и, предположим, четыре голодных друга.

Это значит, что 8 аппетитных кусочков пиццы будут так относиться к 4 голодным друзьям, что каждому голодающему достанется по 2 кусочка. Прекрасно!

А теперь представим, ситуацию, в которой есть только половина аппетитной пиццы, но при этом и голодных друга — всего два.

Что мы имеем: 4 кусочка и 2 друга, претендующих на них.

Это значит, что 4 аппетитных кусочка будут так относиться к 2 голодным друзьям, что каждому из них достанется по 2 кусочка.

Оценив обе ситуации, делаем вывод, что отношение 8/4 пропорционально отношению 4/2. Отношения в пропорции — равные.

Вывод: знание математических пропорций пригодится при заказе пиццы. Быстренько прикидываем отношение количества человек, претендующих на пиццу, и число кусочков — и сразу заказываем побольше пиццы, чтобы никто не остался голодным😉

Основное свойство пропорции

Запомните основное свойство пропорции:

Произведение крайних членов пропорции равно произведению средних членов этой пропорции.

В виде формулы свойство выглядит так:

a : b = c : d
a * d = b * c

Мы знаем, что a и d — крайние члены пропорции, b и c — средние.

Это свойство следует применять, чтобы проверить пропорцию. Если все сходится согласно формулировке — пропорция составлена верно, и отношения в пропорции являются равными друг другу.

Давайте проверим несколько пропорций.

Пример 1. Дана пропорция:6/2 = 12/4

Делаем вывод, что пропорция 6/2 = 12/4 составлена верно.

Пример 2. Дана пропорция: 10/2 = 16/4

Отсюда делаем вывод, что отношения в пропорции 10/2 ≠ 16/4 не являются равными.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Примеры решения задач с пропорцией

Чтобы потренироваться в составлении пропорций, решим вместе несколько задачек.

Задачка 1. Дана математическая пропорция: 15/3 = x/4

Ответ: в пропорции 15/3 = x/4, x = 20

Задачка 2. Найдите четвертый член пропорции: 18, 9 и 24.

Ответ: четвертый член пропорции — 12.

Задачка 3. 18 человек могут съесть пять килограммов суши за 8 часов, сколько часов понадобится 9 людям?

Ответ: 16 часов понадобится 9 людям, чтобы съесть все суши.

Задачка 4. Дана пропорция: 20/2 = y/4

Источник

Урок 22 Бесплатно Пропорции

Чтобы узнать название темы урока, обратите внимание на картинку.

Попробуйте отгадать ребус.

На этом уроке вы узнаете, что называют пропорцией, выведете основное свойство пропорции и с помощью него научитесь решать задачи и уравнения.

Пропорция

В IV веке до н.э. древнегреческий математик Евдокс Книдский дал определение пропорции, состоящей из величин любой природы, а не только из натуральных величин.

Пропорции применяли с древности при решении различных задач.

Древние греки использовали пропорцию и ее свойство для строительства сооружений, при создании произведений искусства (скульптуры, статуи), в ремесленническом деле и др.

Соблюдение пропорций, определенных соотношений, активно используется и в настоящее время в архитектуре, искусстве, музыке, при решении физических задач.

В географии и моделировании пропорциональные зависимости применяют при создании уменьшенной копии реального объекта.

В химии для проведения успешной реакции рассчитывают пропорциональное отношение химических веществ.

В медицине и фармацевтике используют пропорции при изготовлении лекарственных препаратов.

В кулинарии, например, с помощью пропорции можно рассчитать рецепт одного и того же блюда для разного количества гостей.

Разберем, что же такое пропорция в математическом понимании.

Возьмем два отношения: \(\mathbf<\frac<36><9>>\) и \(\mathbf<\frac<12><3>>\) и эти отношения равны, так как \(\mathbf<36\div9=4>\) и \(\mathbf<12\div3=4>\), значит \(\mathbf<\frac<36><9>= \frac<12><3>>\)

Равенство двух отношений называют пропорцией.

С помощью букв запишем пропорцию из двух отношений так: \(\mathbf\) или \(\mathbf<\frac= \frac>\).

Эту математическую запись читают так: «Отношение a к b равно отношению c к d» или «a так относится к b, как c относится к d».

Все члены пропорции не равны нулю: \(\mathbf\).

Числа a и d называют крайними членами пропорции.

Числа b и c называют средними членами пропорции.

У меня есть дополнительная информация к этой части урока!

В мире существует «золотая пропорция», которую называют «золотым сечением». Это пропорциональное деление отрезка на различные по размеру части, но в таком соотношении к друг другу, что меньший отрезок так относится к большему, как больший ко всей величине.

Приблизительное значение «золотого сечения» равно 1,618… Число это продолжается бесконечно после запятой, и оно не периодично.

В процентном выражении целая часть относится к большей, как большая к меньшей, примерно так: 62% и 38% соответственно.

Обозначают число «золотого сечения» математической буквой \(\mathbf<\varphi>\) (фи).

Мир живой и неживой природы, мир творений человека полон красоты, симметрии и гармонии. Этот мир описывается законом «золотого сечения».

Рассмотрим только несколько примеров, где присутствует и используется правило «золотого сечения».

Считается, что длина фаланг пальцев и длина кисти руки, средний палец и мизинец, или высота лица и расстояние от кончика подбородка до центральной точки соединения губ у пропорционального человека находятся в определенных отношениях, соответствуя правилу «золотого сечения».

Форма тела ящериц, стрекоз, бабочек соответствует закону «золотого сечения»: отношение грудной и брюшной части тела приближенно равны значению «золотого сечения».

Спиралевидная форма ракушек тоже описывается числом \(\mathbf<\varphi>\) (фи).

«Золотая пропорция» была обнаружена в египетских пирамидах, произведениях искусства, архитектуре и применяется до сих пор в разных областях жизни человека

Пройти тест и получить оценку можно после входа или регистрации

Источник

Пропорции в математике с примерами решения и образцами выполнения

Определение пропорции:

Связь между четырьмя алгебраическими выражениями А, В, С и D, имеющая вид

называется пропорцией.

(Равенство 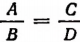теряет смысл и перестает быть пропорцией как при В = О, так и при D = 0. Оно теряет смысл и перестает быть пропорцией и тогда, когда В и D равны нулю одновременно.)

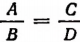
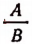
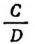
В пропорции величины А и D называются крайними, а В и С средними членами. Далее выражение называется первым отношением, а вторым; А и С называются предыдущими членами этих отношений, а В и D —последующими.

Главное свойство пропорции

Умножив левую и правую части пропорции

на произведение bd, получим ad = be, т. е. во всякой пропорции произведение крайних членов равно произведению средних.

Составление пропорции по данному равенству двух произведений

Пусть pq = ху. Разделив левую и правую части этого равенства на qx, получим

Этот результат можно сформулировать следующим образом.

Если произведение двух чисел равно произведению двух других, то из этих четырех чисел можно составить пропорцию, беря множители одного произведения за крайние, а множители другого произведения за средние члены пропорции. (При этом дополнительно требуется, чтобы оба последующих члена пропорции не оказались равными нулю.)

Перестановка членов пропорции

Пусть ad = be и числа а, b, с, d — все отличны от нуля. Разделив левую и правую части равенства ad = bc первый раз на bd, второй на ab, третий на ас и четвертый на cd, получим соответственно четыре пропорции:

Поменяв местами отношения в этих равенствах, получим еще четыре пропорции:

Этот результат показывает, что в пропорции можно менять местами средние и крайние члены и ставить оба крайних члена на места средних, а оба средних на места крайних.

Производные пропорции

1. Прибавив к левой и правой частям пропорции по единице, получим

т. е. во всякой пропорции сумма членов первого отношения так относится к своему последующему, как сумма членов второго отношения — к своему последующему.

2. Вычтя из левой и правой частей пропорции по единице, получим:

т. е. во всякой пропорции разность членов первого отношения так относится к своему последующему, как разность членов второго отношения — к своему последующему.

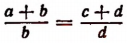
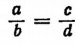
3. Разделив левую часть равенства на левую часть равенства и правую на правую, получим:

т. е. во всякой пропорции сумма членов первого отношения так относится к своему предыдущему, как сумма членов второго отношения — к своему предыдущему.

4. Разделив левую часть равенства 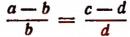на левую часть равенства и правую на правую, получим:

т. е. во всякой пропорции разность членов первого отношения так относится к своему предыдущему, как разность членов второго отношения —к своему предыдущему.

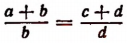
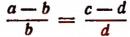
5. Разделив левую часть равенства на левую часть равенства и правую на правую, получим:

т. е. во всякой пропорции сумма членов первого отношения так относится к их разности, как сумма членов второго отношения — к их разности.

Из пропорции мы вывели пять производных пропорций. Однако надо иметь в виду, что из пропорции можно было бы получить сколько угодно производных пропорций.

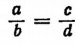
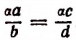
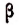
Например, умножив обе части пропорции на число а, получим . Прибавив к левой и правой частям последнего равенства число , будем иметь, что

т. е. получим новую производную пропорцию.

Определение неизвестного члена пропорции

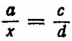
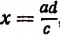
Пусть в пропорции числа а, с, d известны, a х изображает число неизвестное. Тогда по свойству пропорции cx = ad, откуда , т. е. неизвестный средний член пропорции равен произведению крайних членов, деленному на известный средний. Аналогично определяется и неизвестный крайний член.

Примеры:

1. Найти неизвестное число х из пропорции 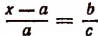, где а, b и с числа известные.

Составим производную пропорцию по правилу: сумма членов первого отношения так относится к своему последующему члену, как сумма членов второго отношения к своему последующему:

2. Найти неизвестное х из пропорции 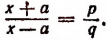Составим производную пропорцию по правилу: сумма членов первого отношения так относится к их разности, как сумма членов второго отношения к их разности, т. е.

Ряд равных отношений

Основное свойство ряда равных отношений

Пусть имеется ряд равных отношений:

Обозначим общее значение всех этих отношений буквой k. Тогда

Складывая левые и правые части этих равенств, получим:

Итак, доказано следующее:

если несколько отношений равны друг другу, то отношение суммы их предыдущих членов к сумме последующих равно каждому из этих отношений.

Пример:

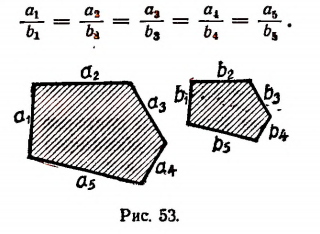
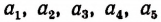
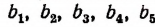
Пусть длины сторон одного многоугольника (рис. 53) пропорциональны длинам сторон другого многоугольника, т. е.

По свойству ряда равных отношений получим:

где Р и Q периметры многоугольников.

Прямая пропорциональность

Сначала рассмотрим несколько примеров.

Пример:

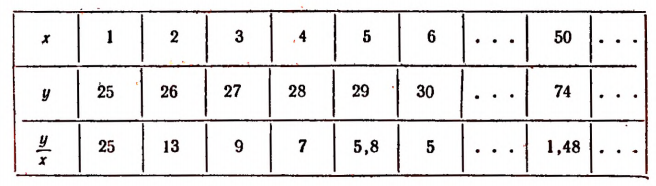
Пусть буква х обозначает в годах возраст сына, а буква у — возраст отца и пусть в данный момент сыну один год, а отцу 25 лет.

Составим таблицу значений х и соответствующих им значений буквы у. В третьей строке этой таблицы выпишем значения отношения :

В этом примере отношение (отношение возраста отца к возрасту сына) не остается неизменным. Оно с течением времени убывает.

Пример:

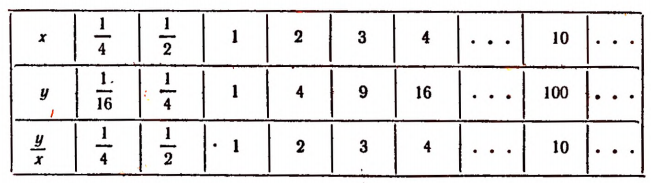
Пусть буква х обозначает в сантиметрах длину стороны квадрата, а буква у — площадь квадрата в квадратных сантиметрах.

Составим таблицу, подобную предыдущей.

Отношение и здесь не остается неизменным. Оно возрастает при возрастании х.

Пример:

Пусть буква х обозначает в кубических сантиметрах объем ртути при температуре 0°, а буква у — вес этой ртути в граммах. Известно, что 1 куб. см ртути при температуре 0° весит 13,6 г.

Опять составим таблицу значений х, у и .

Этот третий пример существенно отличается от двух предыдущих. Здесь отношение сохраняет неизменное значение.

Определение:

Две величины у и х называются прямо пропорциональными (или просто пропорциональными), если при всех их возможных изменениях отношение остается равным одному и тому же числу и если при х = 0 значение у также равно нулю.

Значит, вес ртути и объем ртути при постоянной температура являются величинами пропорциональными.

Возраст отца и возраст сына не пропорциональны.

Также не пропорциональны сторона квадрата и его площадь.

Пусть изменяющиеся величины у и х пропорциональны. Тогда отношение будет равно некоторому постоянному числу.

Обозначая это постоянное число буквой k, получим:

Следовательно, если величины у и х пропорциональны и отношение равно k, то у выражается в зависимости от х формулой

Число k называется коэффициентом пропорциональности (величины у по отношению к величине х).

Теперь докажем обратное положение. Пусть

где k — постоянное число.

Отсюда следует, что при х = 0 и у = 0 и что 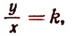А это и означает, что величины у и х пропорциональны.

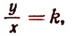
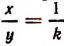
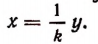
Из того что следует, что , или что Отсюда можно сделать следующий вывод:

Если коэффициентом пропорциональности величины у по отношению к величине х служит постоянное число k, то коэффициентом пропорциональности величины х по отношению к величине у будет служить число .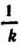

Приведем еще один пример пропорциональных величин. Путь s, пройденный при равномерном движении, пропорционален. времени t, т. е.

Здесь постоянное число v есть коэффициент пропорциональности величины s по отношению к величине t (v есть скорость равномерного движения).

Сделаем еще два замечания.

Замечание:

Если имеется два ряда чисел:

то числа одного из этих рядов называются пропорциональными числам другого ряда.

Замечание:

Если имеются только два постоянных числа а и b, то бессмысленно говорить о них, что они пропорциональны или не пропорциональны.

В этом случае можно интересоваться либо характером этих чисел, либо их разностью, либо их отношением и т. д.

В заключение решим две простые задачи на пропорциональные величины.

Задача:

На карте в масштабе расстояние между двумя пунктами равно 42,5 см. Определить, чему равно это расстояние на карте в масштабе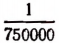

Решение:

Длина на карте прямо пропорциональна масштабу. Поэтому.

Задача:

С помощью непосредственного измерения установили, что при повышении температуры рельса на 24°С его длина увеличивается на 1,5 мм. Требуется вычислениями определить изменение длины рельса при понижении его температуры на 40°С. (Считать изменение длины рельса величиной, прямо пропорциональной изменению температуры.)

Решение:

Обозначив искомое изменение (в мм) буквой х, получим:

т. е. при понижении температуры рельса на 40°С его длина сократится на 2,5 мм.

Обратная пропорциональность

Сначала приведем примеры.

1. Рассмотрим изменяющийся прямоугольный параллелепипед с квадратным основанием, имеющий неизменный объем, равный 3600 куб. см (рис. 54).

Пусть буква х обозначает в сантиметрах изменяющуюся сторону основания, а буква у — изменяющуюся высоту параллелепипеда.

легко видеть, что произведение ху не остается неизменным при постоянстве объема.

2. Рассмотрим изменяющийся прямоугольник, имеющий неизменную площадь, равную 100 кв. см.

Пусть буква х обозначает одно изменяющееся измерение (например, длину прямоугольника), а буква у — другое изменяющееся измерение (ширину). Пусть х и у выражены в сантиметрах.

Так как произведение измерений прямоугольника равно его площади, то величины х и у при всех своих возможных изменениях будут давать в своем произведении число 100, т. е. произведение изменяющихся величин х и у будет оставаться неизменным.

Существенное отличие второго примера от первого заключается в том, что в нем произведение ху остается неизменным, в то время как в первом оно изменяется.

Определение:

Две величины х и у называются обратно пропорциональными, если при всех их возможных изменениях произведение ху остается равным одному и тому же числу.

Обозначая это число буквой k, получим

Следовательно, если величины х и у обратно пропорциональны, то величина у выражается через величину х по формуле следующего вида:

Число k называется коэффициентом обратной пропорциональности.

Длина прямоугольника и ширина прямоугольника при заранее заданной площади прямоугольника являются величинами обратно пропорциональными. Коэффициентом обратной пропорциональности служит как раз эта площадь.

Сторона основания прямоугольного параллелепипеда с квадратным основанием и высота параллелепипеда при заранее заданном объеме не являются величинами обратно пропорциональными.

Задача:

Зал освещается m лампами по а свечей каждая. Сколькими лампами в b свечей можно получить ту же освещенность зала?

Число ламп и число свечей каждой лампы при данной освещенности зала являются величинами обратно пропорциональными. Поэтому, обозначая число ламп в b свечей буквой x, получим

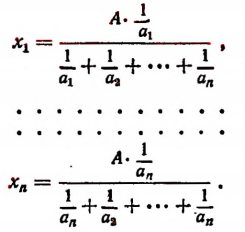
Пропорциональное деление

Задача:

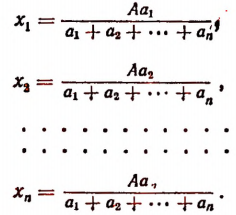
Число А разделить на n слагаемых прямо пропорционально числам

Обозначим искомые слагаемые буквами 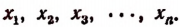Тогда по условию задачи

Пользуясь свойством ряда равных отношений, получим

Задача:

Число А разделить на n слагаемых обратно пропорционально числам

Обозначим искомые слагаемые буквами 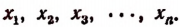Тогда согласно условию задачи

По свойству ряда равных отношений получим

Пропорции и пропорциональная зависимость

члены а и d называются крайними, а b и с средними.

При изложении свойств пропорции будем считать, что ни один из членов пропорции не равен нулю.

Пример:

отношение числа 7 к числу 2. Предыдущий член здесь 7, последующей 2.

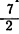
Пример:

пропорция. Крайние члены здесь 10 и 2, средние— 4 и 5.

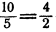
Главное свойство пропорции

Теорема:

Во всякой пропорции произведение крайних
членов равно произведению средних.

Доказательство:

Умножим обе части равенства (1) на bd, получим

Теорема:

Если произведение двух чисел
равно произведению двух других чисел, то из этих четырех чисел можно составить пропорцию^ крайними членами которой являются сомножители одного из двух произведений, а средними—сомножители другого.

При этом предполагается, что ни один из сомножителей не равен нулю.

Доказательство:

a, b, с, d все отличны от нуля. Разделим обе части равенства на bd, получим

Пример:

— пропорция. Произведение крайних ее членов равно 20, произведение средних ее членов также равно 20.

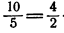
Пример:

8 • 9 = 3 • 24 — равенство двух произведений.
Разделим обе части этого равенства на 9 • 24, получим пропорцию

Определение неизвестного члена пропорции

Теорема:

Средний член пропорции равен произведению крайних, деленному на другой средний. Крайний член пропорции равен произведению средних, деленному на другой крайний.

На основании теоремы 1 имеем

Разделим обе части равенства (4) на с, получим равенство (2). Разделим обе части равенства (4) на d, получим равенство (3). Теорема доказана.

Пример:

Найти х, если

Решение:

Пример:

Найти х, если

Решение:

Перестановка членов пропорции

Теорема:

Во всякой пропорции можно переставить
средние члени, переставить крайние члени, переставить и средние члени и крайние, средние поставить на место крайних, а крайние на место средних.

Иными словами, если

(переставлены средние члены),

(в (1) переставлены крайние члены),

(в (1) переставлены и средние и крайние члены),

(средние поставлены на место крайних, крайние — на место средних).

Доказательство:

Разделим обе части равенства (6) на cd, получим равенство (2). Точно так же, разделив обе части равенства (6) на аb, а затем на ас, получим равенства (3) и (4). Равенство (5) получается из равенства (4) посредством перестановки отношений. Теорема доказана.

Следствие:

Переставим отношения в равенствах (I), (2), (3), получим еще три пропорции

Таким образом, всякую пропорцию посредством перестановки ее членов можно представить в восьми различных видах.

Производные пропорции

Теорема:

1) Во всякой пропорции сумма членов первого отношения так относится к последующему члену этого отношения, как сумма членов второго отношения относится к своему последующему.
2) Во всякой пропорции разность членов первого отношения так относится к последующему члену этого отношения, как разность членов второго отношения относится к своему последующему.

Иными словами, если

Доказательство:

Прибавим к каждой части равенства (1)
по 1, получим равенство (2). Вычтем из каждой части равенства (1) по 1, получим равенство (3). Теорема доказана.

Теорема:

1) Во всякой пропорции сумма членов первого отношения так относится к предыдущему члену этого отношения, как сумма членов второго отношения относится к своему предыдущему.
2) Во всякой пропорции разность членов первого отношения так относится к предыдущему члену этого отношения, как разность членов второго отношения относится к своему предыдущему.

Иными словами, если

Доказательство:

Разделим равенство (2) почленно на
равенство (1), т. е., левую часть равенства (2) разделим на левую часть равенства (1), а правую часть равенства (2) на правую часть равенства (1). Получим равенство (4). Разделив равенство (3) почленно на равенство (1), получим равенство 5). Теорема доказана.

Теорема:

Во всякой пропорции сумма членов первого
отношения так относится к их разности, как сумма членов второго отношения относится к их разности, если только эти разности отличны от нуля.

Иными словами, если

Доказательство:

Разделив почленно равенство (4) на
равенство (5), получим равенство (6).

Ряд равных отношений

Теорема:

Если даны несколько равных отношений* то
сумма всех предыдущих членов отношений относится к сумме всех последующих как любой из предыдущих к своему последующему.

Доказательство:

Пусть имеется несколько равных отношений

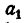
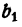
Обозначим результат деления на буквой q. Так как все отношения ряда (1) равны между собой, каждое из них также равно q. Таким образом,

Сложив почленно все равенства (2), имеем

Задача:

Доказать, что при любых 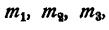отличных от нуля,

Решение:

Умножим каждый, член первого отношения на 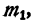получим пропорцию

На основании теоремы 8 имеем

Задача:

Решить уравнение

Решение:

Пользуясь теоремой 7 § 5, имеем

Пропорциональная зависимость

Мы много раз составляли уравнения, выражающие зависимость между величинами, и могли наблюдать, что. зависимости эти бывают весьма разнообразны.

При решении многих задач мы встречаемся с двумя величинами, зависимость между которыми такова, что при изменении этих величин их отношение остается неизменным. Такие величины называются прямо пропорциональными, а зависимость между ними — пропорциональной зависимостью.

Для примера приведем несколько задач, в которых мы встретимся с величинами, находящимися в пропорциональной зависимости.

Задача:

Скорость течения реки 3 км в час. Плот за t часов прошел вниз по реке S км. Составить уравнение, выражающее зависимость между S и t.

Задача:

С каждого гектара собрано 30 ц ржи и, таким образом, с k га собрано А ц. Составить уравнение, выражающее зависимость между А и k.

Задача:

Основание прямоугольника 2 см, высота h см, площадь Q 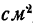. Составить уравнение, выражающее зависимость между Q и h.

Задача:

1 м материи стоит 20 руб. За m м этой материи
уплатили N pyб. Составить уравнение, выражающее зависимость между N и m.

Мы рассмотрели четыре задачи, которые по своему содержанию относятся к различным областям практической деятельности. Нетрудно убедиться, что в каждой из этих задач мы действительно имеем дело с прямо пропорциональными величинами.

Так, в первой задаче отношение расстояния (в kм), пройденного плотом, к времени (в часах), в течение которого плот находился в пути, всегда одно и то же и равно 3. Поэтому расстояние, которое проходит плот вниз по реке, пропорционально времени, в течение которого плот находится в пути, при условии, что скорость течения реки повсюду одна и та же.

Точно так же во второй задаче количество ржи, собранной с нескольких гектаров, пропорционально количеству ржи, собранной с одного гектара, при условии, что с каждого гектара собрано по одному и тому же количеству ржи и т. д.

Заметим, что уравнения, к которым мы пришли в рассмотренных задачах, имеют один и тот же вид. В этих уравнениях одна, из величин равна произведению некоторого числового множителя на другую величину. Этот множитель называется коэффициентом пропорциональности. В первой задаче коэффициент
пропорциональности равен 3, во второй задаче он равен 30, в третьей задаче он равен 2, в четвертой задаче он равен 20.

Таким образом, пропорциональная зависимость между величинами всегда выражается уравнением y = kx, где k — коэффициент пропорциональности. Известно, что зависимость между двумя величинами может быть наглядно представлена таблицей, а затем и графиком.

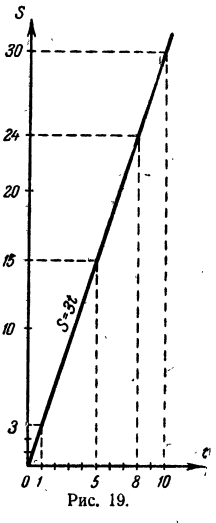
Для примера представим таблицей зависимость, выражаемую уравнением S = 3/ (первая задача):

Построим график зависимости S = 3t (рис. 19). Обратим внимание на следующие обстоятельства:

и т. д. (для первого столбца это отношение не имеет смысла; так как на нуль делить нельзя).

2, График представляет собой луч, выходящий из начала координат (при t= 0, S = 0). (Доказательство этого утверждения здесь провести нельзя, так как для этого требуются некоторые сведения из геометрии.)

То же самое можно наблюдать и при графическом представлении любой другой пропорциональной зависимости между двумя величинами.

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник