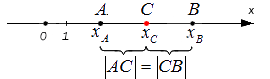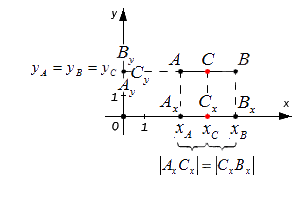Как указать середину отрезка
Нахождение координат середины отрезка: примеры, решения
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
И далее мы рассмотрим, как же определять координаты середины отрезка (точки C ) при заданных координатах концов отрезка ( A и B ), расположенных на координатной прямой или в прямоугольной системе координат.
Середина отрезка на координатной прямой
Из первого равенства выведем формулу для координаты точки C : x C = x A + x B 2 (полусумма координат концов отрезка).
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
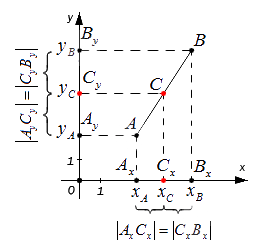
Середина отрезка на плоскости
x C = x A + x B 2 и y C = y A + y B 2
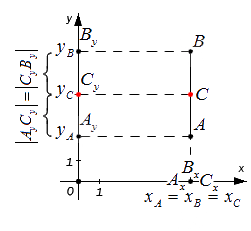
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
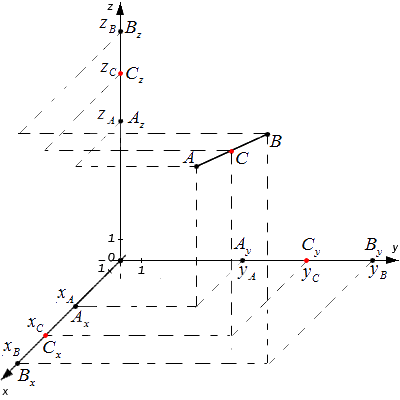
Середина отрезка в пространстве
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Следовательно, точка C имеет координаты:
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Решение
Решение
Ответ: 58
Решение
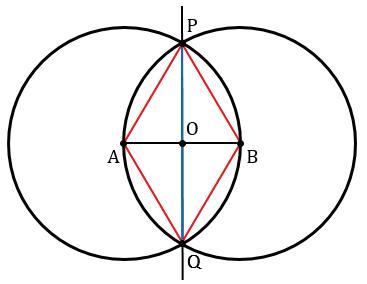
Построение середины отрезка
Пример:
Дано: отрезок АВ.
Построить: середину АВ.
Решение:
Строим с помощью линейки произвольный отрезок АВ.
Далее с помощью циркуля строим две окружности радиуса АВ с центрами в точках А и В.
Получаем две точки пересечения данных окружностей. Обозначим их Р и Q. Проведем с помощью линейки через точки Р и Q прямую РQ.
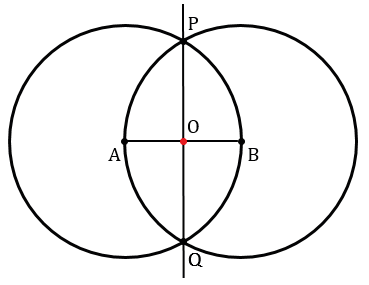
Точку пересечения прямой РQ и отрезка АВ обозначим О.
Рассмотрим треугольники РАQ и РВQ.
Поделись с друзьями в социальных сетях:
Координаты середины отрезка
Что такое середина отрезка
Отрезок — это геометрическая фигура, представляющая собой ограниченный с двух сторон участок прямой.
Пусть точки A и B не совпадают. Если провести через них прямую, то образуется отрезок AB или BA, который ограничен точками A и B. Данные точки являются концами отрезка.
Длина отрезка — это расстояние между двумя точками, ограничивающими данный отрезок. Длина отрезка AB обозначается как модуль данной геометрической фигуры, то есть |AB|.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Серединой отрезка является такая точка C, принадлежащая отрезку AB, которая расположена в центре данного отрезка, то есть |AC|=|CB|.
Правила нахождения координат середины отрезка, формулы
Середина отрезка на координатной прямой
Предположим, что несовпадающие точки A и B лежат на координатной прямая Ох. Известно, что A и B соответствуют действительные числа xA и xB, а точка С делит AB пополам. Определите координату xC, соответствующую С.
Так как C — это середина AB, то справедливо следующее равенство:
Вычислим расстояние между A и C, а также между C и B. Для этого определим модуль разницы их координат. На математическом языке это будет иметь вид:
Опустим знак модуля и получим справедливость двух выражений:
Исходя из первого равенства, получим формулу нахождения xC, согласно которой координата точки С равна половине суммы координат A и B:
Следствием второго равенства будет следующее утверждение:
Это противоречит заданным условиям, следовательно, формула определения координат середины отрезка выглядит так:
Середина отрезка на плоскости
В декартовой системе координат Oxy расположены две точки A(xA,yA) и B(xB,yB), которые не совпадают между собой. Точка C является центром AB. Необходимо произвести вычисление координат xC и yC, соответствующих С.
Пусть произвольные точки А и В лежат на одной координатной прямой, а также не принадлежат прямым, располагающимся перпендикулярно к оси абсцисс или ординат. Опустим от заданных точек A, B, C перпендикуляры на ось x на ось y. Полученные точки пересечения с осями координат Ax, Ay; Bx, By; Cx, Cy — это проекции исходных точек.
По построению прямые AAx, BBx, CCx относительно друг друга находятся параллельно. Прямые AAy, BBy, CCy не пересекаются, то есть являются параллельными. Согласно равенству AB=BC, далее применим теорему Фалеса и получим:
Это значит, что Cx и Cy являются серединами отрезков AxBx и AyBy соответственно. Теперь воспользуемся формулой определения координат середины отрезка на координатной прямой и получим:
Данные формулы подходят для вычисления координат середины отрезка в случае его расположения на осях абсцисс и ординат, а также при перпендикулярности одной из них. Следовательно, координаты центра отрезка AB, находящегося в плоскости и ограниченного точками A(xA,yA) и B(xB,yB), вычисляются следующим образом:
Середина отрезка в пространстве
Допустим, что в трехмерной системе координат Oxyz любые две точки с соответствующими им координатами A(xA, yA, zA) и B(xB, yB, zB). C(xC, yC, zC) — это центр АВ. Задание заключается в том, чтобы определить xC, yC, zC.
Проведем от исходных точек перпендикуляры к прямым Ox, Oy и Oz. Образовавшиеся точки пересечения с координатными осями — Ax, Ay, Az; Bx, By, Bz; Cx, Cy, Cz — проекции точек A, B, C на них.
Воспользуемся теоремой Фалеса:
Исходя из полученных равенств следует, что Cx, Cy, Cz — делят AxBx, AyBy, AzBz пополам, то есть являются серединами перечисленных отрезков. Значит, для определения координат центра AB с концами A(xA,yA,zA) и B(xB,yB,zB) используем формулу:
Метод с использованием координат радиус-векторов концов отрезка
Трактовка векторов в алгебре позволяет составить формулу для расчета координат середины отрезка.
Дано: прямоугольная система координат Oxy, в которой лежат произвольные точки A(xA,yA) и B(xB,yB), а также C, делящая пополам отрезок, ограниченный A и B.
По определению действий над вектором в геометрии:
Это значит, что С — это центр диагоналей.
Произведем подстановку в формулу (1):
Получили формулу определения координат середины отрезка, находящегося в декартовой системе координат:
По аналогично схеме можно вывести формулу для расчета координат центра отрезка, лежащего в пространстве:
Примеры решения задач
Дано: в декартовой системе координат имеются точки M(5,4) и N(1,−2). Найти координаты середины отрезка MN.
Пусть точка O — центр MN. Тогда вычислим ее координаты, подставив в формулы:
Точка O имеет координаты (3,1).
Дано: треугольник ABC лежит в прямоугольной системе координат. Известны координаты его вершин: A(7,3), B(−3,1), C(2,4). Вычислите длину медианы АМ.
Поскольку АМ является медианой треугольника ABC, то точка М делит сторону ВС на два равных отрезка, то есть является серединой отрезка ВС. Отсюда можно вычислить координат точки М:
Теперь, зная координаты начала и конца отрезка АМ, применим формулу нахождения расстояния между точками:
Формула нахождения координаты середины отрезка
Вы будете перенаправлены на Автор24
Начальные геометрические сведения
Понятие отрезка, как и понятие точки, прямой, луча и угла, относится к начальным геометрическим сведениям. С перечисленных понятий начинается изучение геометрии.
Под «начальными сведениями» обычно понимают нечто элементарное и простое. В понимании, возможно, это так и есть. Тем не менее, такие простые понятия часто встречаются и оказываются необходимыми не только в нашей повседневной жизни, но и в производстве, строительстве и прочих сферах нашей жизнедеятельности.
Начнём с определений.
Рисунок 1. Отрезок. Автор24 — интернет-биржа студенческих работ
Рисунок 2. Середина отрезка. Автор24 — интернет-биржа студенческих работ
Готовые работы на аналогичную тему
Введём простое наблюдение. Если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих отрезков.
Формула нахождения координаты середины отрезка
Формула нахождения координаты середины отрезка относится к курсу аналитической геометрии на плоскости.
Дадим определение координатам.
В нашем случае, координаты отмечаются на плоскости, определённой координатными осями.
Рисунок 3. Координатная плоскость. Автор24 — интернет-биржа студенческих работ
Координаты точек в такой системе определяются двумя числами.
Существуют разные формулы (уравнения), определяющие те или иные координаты. Обычно в курсе аналитической геометрии изучают разные формулы прямых, углов, длины отрезка и прочие.
Перейдём сразу к формуле координаты середины отрезка.
Рисунок 4. Формула нахождения координаты середины отрезка. Автор24 — интернет-биржа студенческих работ
Практическая часть
Примеры из школьного курса геометрии достаточно просты. Рассмотрим несколько основных.
Для лучшего понимания, рассмотрим для начала элементарный наглядный пример.
Рисунок 5. Отрезки на плоскости. Автор24 — интернет-биржа студенческих работ
Рассмотрим другой простой пример, в котором нужно вычислить длину.
Прочие подобные примеры обычно идентичны и ориентированы на умение сопоставлять значения длин и их представление с алгебраическими действиями. Нередко в задачах встречаются случаи, когда сантиметр не укладывается ровное количество раз в отрезок. Тогда единицу измерения делят на равные части. В нашем случае сантиметр делится на 10 миллиметров. Отдельно измеряют остаток, сравнивая с миллиметром. Приведём пример, демонстрирующий такой случай.
Если в очередной задаче возникают трудности с пониманием её решения (например, нетипичные случаи с несколькими отрезками, образующими углами и прочими усложнениями), то лучше рассмотреть задачу, сделав по её условию рисунок. Наглядность способствует лучшему пониманию и более скорому нахождению решения.
Теперь решим задачи по аналитической геометрии.
Подставим значения и получим уравнения:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 08 05 2021
Онлайн калькулятор. Середина отрезка
Предлагаю вам воспользоваться онлайн калькулятором для вычисления середины отрезка AB.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление координат середины отрезка и закрепить пройденный материал.
Калькулятор для вычисления координат середины отрезка AB
Выберите необходимую вам размерность:
Введите координаты точек.
Ввод данных в калькулятор для вычисления координат середины отрезка
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора для вычисления координат середины отрезка
Теория. Середина отрезка.
Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка.
| xc = | xa + xb | ; | yc = | ya + yb |
| 2 | 2 |
| xc = | xa + xb | ; | yc = | ya + yb | ; | zc = | za + zb |
| 2 | 2 | 2 |