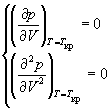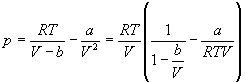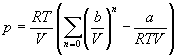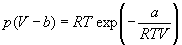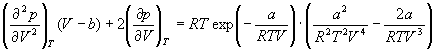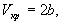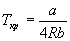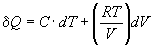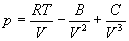Докажите с помощью примеров и логических рассуждений что температура параметр состояния системы
Докажите с помощью примеров и логических рассуждений что температура параметр состояния системы
Глава 1. Основы химической термодинамики
1. Основные понятия термодинамики
Примеры функций состояния: энергия U, энтальпия H, энергия Гельмгольца F, энергия Гиббса G, энтропия S. Термодинамические параметры объем V, давление p, температуру T также можно считать функциями состояния, т.к. они однозначно характеризуют состояние системы. Примеры функций перехода: теплота Q и работа A.
Все выводы и соотношения термодинамики основаны на двух постулатах (исходных положениях) и трех законах (началах).
Первое исходное положение, или основной постулат термодинамики:
Любая изолированная система с течением времени приходит в равновесное состояние и самопроизвольно не может из него выйти.
Переход системы в равновесное состояние называют релаксацией. Основной постулат термодинамики ничего не говорит о времени релаксации. В классической равновесной термодинамике вообще нет времени. Термодинамика позволяет установить только возможность протекания процессов, но не может определить скорость этих процессов.
Второе исходное положение, или нулевой закон термодинамики описывает свойства систем, находящихся в состоянии теплового равновесия:
Если система А находится в тепловом равновесии с системой В, а та, в свою очередь, находится в равновесии с системой С, то системы А и С также находятся в тепловом равновесии.
Из нулевого закона следует, что при равновесии внутренние параметры системы являются функциями внешних параметров и температуры. Уравнение, связывающее внутренние параметры с внешними параметрами и с температурой, называют уравнением состояния термодинамической системы. В общем случае уравнение состояния имеет вид:
(1.2) называют калорическим.
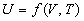
Если известны термическое и калорическое уравнения состояния, то с помощью законов термодинамики можно определить все термодинамические свойства системы, т.е. получить ее полное термодинамическое описание. Сами уравнения состояния нельзя вывести методами классической термодинамики, но их можно определить экспериментально.
Для описания реальных газов, в которых частицы имеют конечные размеры и взаимодействуют друг с другом, используют более сложные уравнения состояния:
(уравнение Ван-дер-Ваальса)
(уравнение Бертло)
(I уравнение Дитеричи)
(II уравнение Дитеричи)
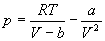
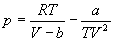
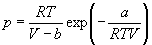
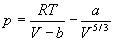
С высокой точностью поведение любого реального газа можно описать с помощью вириального разложения по степеням обратного объема:
(1.4) или давления 
, (1.5)
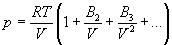
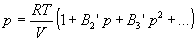
Уравнение состояния идеального газа и вириальное уравнение состояния реального газа можно вывести методами статистической термодинамики.
Иногда уравнения состояния реальных газов записывают через так называемые приведенные переменные, которые определяют через параметры критического состояния газов: pr = p / pкр, Vr = V / Vкр, Tr = T / Tкр, где критические параметры определяются как координаты точки перегиба на изотерме реального газа:
ПРИМЕРЫ
Пример 1-1. Докажите, что при больших объемах уравнение Ван-дер-Ваальса переходит в уравнение идеального газа.
Решение. Уравнение Ван-дер-Ваальса:
.
.
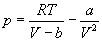
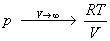
Пример 1-2. Найдите вириальные коэффициенты Bi для газа, подчиняющегося уравнению Ван-дер-Ваальса.
Решение. В уравнении Ван-дер-Ваальса выделим сомножитель RT/V:
Если разложить первое слагаемое в скобке в ряд по степеням b/V, получим:
Из этого разложения следует, что второй вириальный коэффициент газа Ван-дер-Ваальса зависит от температуры:
Пример 1-3. Найдите критические параметры и приведенное уравнение состояния для газа Дитеричи (I уравнение).
Решение. Запишем уравнение Дитеричи в виде:
и продифференцируем левую и правую часть этого уравнения два раза по объему при постоянной температуре:
и учтем, что в критической точке первая и вторая производная равны 0:
,
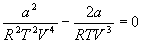
откуда находим: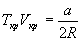 
.
Если продифференцировать обе части уравнения состояния по объему один раз с учетом равенства нулю первой производной, то можно найти второе соотношение между критическими объемом и температурой:
,
.
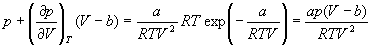
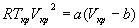
Подставляя сюда первое найденное соотношение для критических параметров, получим:
И, наконец, подставляя эти параметры в уравнение состояния, находим критическое давление:
.
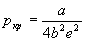
Для вывода приведенного уравнения состояния подставим в уравнение Дитеричи приведенные переменные:
, 
, 
.
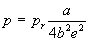
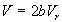
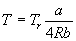
В результате получаем приведенное уравнение Дитеричи, не содержащее индивидуальных параметров:
.
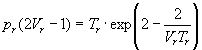
ЗАДАЧИ
1-1. Приведите пример термодинамического процесса, который может совершаться как обратимо, так и необратимо. Назовите для этого процесса по одной функции состояния и перехода.
1-2. Приведите примеры систем со временем релаксации порядка: а) секунд; б) часов; в) десятилетий.
1-3. Изменение теплоты в зависимости от температуры и объема в некоторой системе описывается уравнением:
1-4. Докажите, что при больших объемах первое уравнение Дитеричи переходит в уравнение идеального газа.
1-5. Найдите частные производные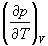 
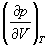
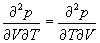
и 
для: а) идеального газа; б) газа Ван-дер-Ваальса; в) газа, подчиняющегося I уравнению Дитеричи. Докажите, что 
.
1-6. Используя вириальные разложения (1.4) и (1.5), найдите связь между вириальными коэффициентами B2, B3 и B2‘, B3‘.
1-7. Найдите критические параметры и приведенные уравнения состояния для газов: а) Ван-дер-Ваальса; б) Бертло.
1-8. Предложено следующее уравнение состояния (для одного моля):
Выразите критические параметры через постоянные B и C и найдите фактор сжимаемости PV/RT в критической точке.
Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору