Докажите что в правильном тетраэдре скрещивающиеся ребра взаимно перпендикулярны

Теорема о трех перпендикулярах

Что такое теорема о трех перпендикулярах простыми словами

Как ее использовать в задачах

Как оформлять на ЕГЭ

Начнем с парочки вводных понятий, ты же хочешь жить по понятиям?

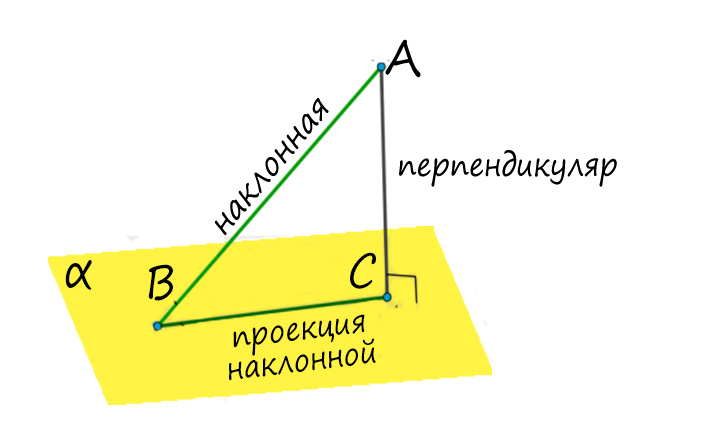
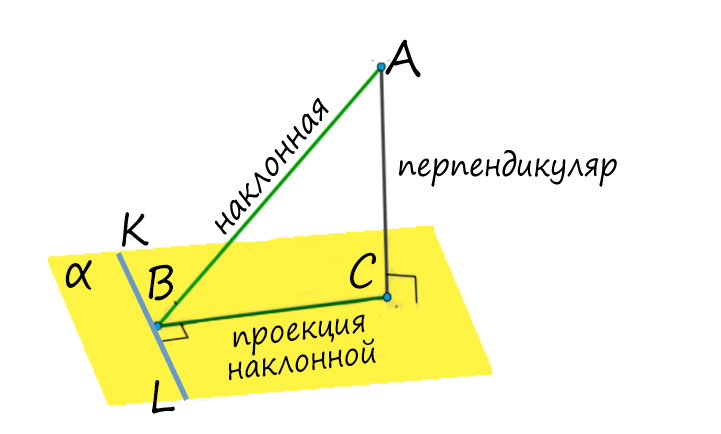
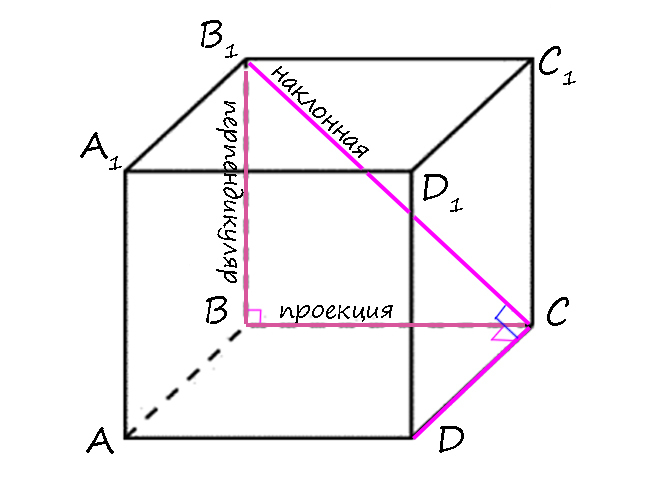
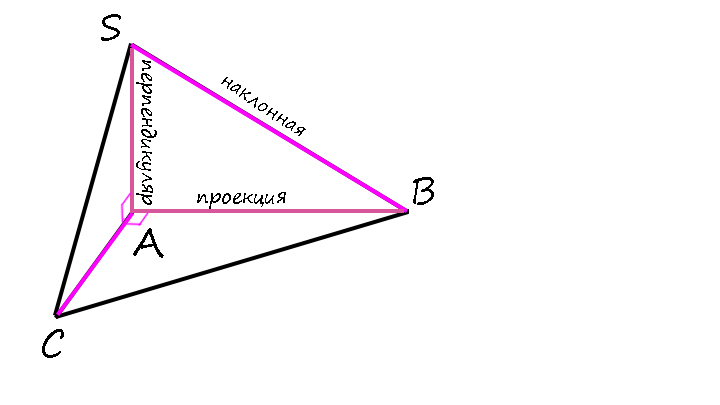
Если в плоскости альфа провести прямую KL через точку В так, что KL ⊥ BC, тогда по теореме о трех перпендикулярах (т.т.п.) KL ⊥ BA.

Словами можно сказать так: прямая, лежащая в плоскости, перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции этой наклонной на данную плоскость (верно и наоборот).

Перейдем к самому распространенному примеру:

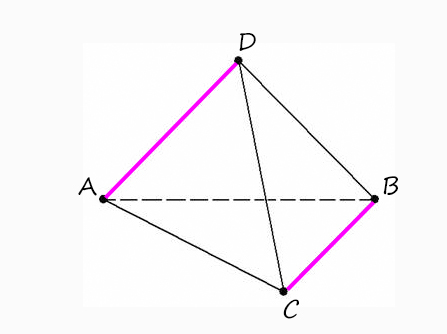
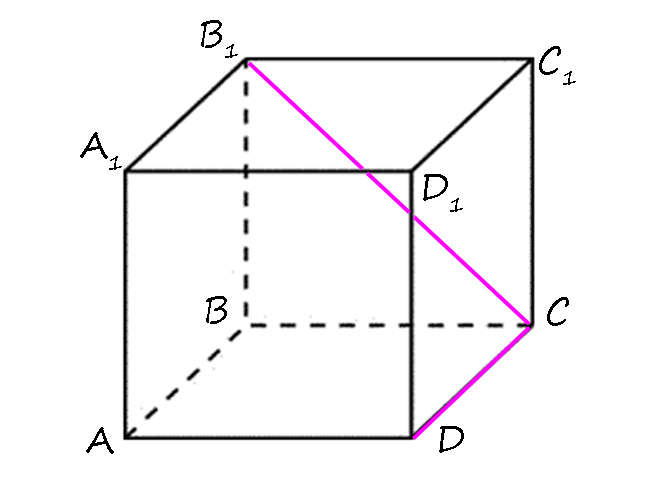
1) Докажите, что в тетраэдре скрещивающиеся ребра перпендикулярны.

У тетраэдра есть три пары скрещивающихся ребер. Докажем перпендикулярность одной пары, другие вы сделаете по аналогии, например, AD ⊥ BC.

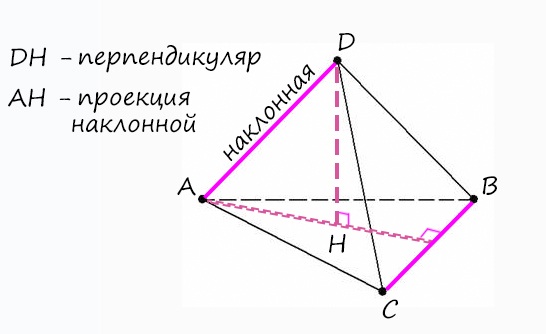
Сейчас есть только наклонная AD и плоскость (ABC), значит, нам не хватает проекции наклонной и перпендикуляра, тогда проведем их:

Тогда, чтобы доказать, что AD ⊥ BC:
1) AH ⊥ BC (если продлить АН до пересечения с BC), т.к. AH является выстой в правильном треугольнике.
2) DH ⊥ (ABC) (по построению, а, значит, перпендикулярно любой прямой, находящейся в этой плоскости) => DH ⊥ BC.

После того, как мы это доказали, можем смело сказать, что AD ⊥ BC (всегда дожно быть доказательство двух пунктов, и только тогда вывод).

2) Докажите, что в прямом параллепипеде ребра B₁C и CD перпендикулярны.

Возьмем B₁C как наклонную к плоскости (ABCD), тогда перпендикуляром будет BB₁, а проекцией наклонной на эту плоскость — BC.

1) BB₁ ⊥ (ABCD) т.к. параллепипед прямой (боковые ребра перпендикулярны плоскости основания) => BB₁ ⊥ CD (если прямая перпендикулярна плоскости, то и перпендикулярна всем прямым, лежащим в этой плоскости).
2) BC ⊥ CD т.к. ABCD — прямоугольник.
3) По т.т.п.: B₁C ⊥ CD.

Два пункта доказательства, третий пункт вывод.

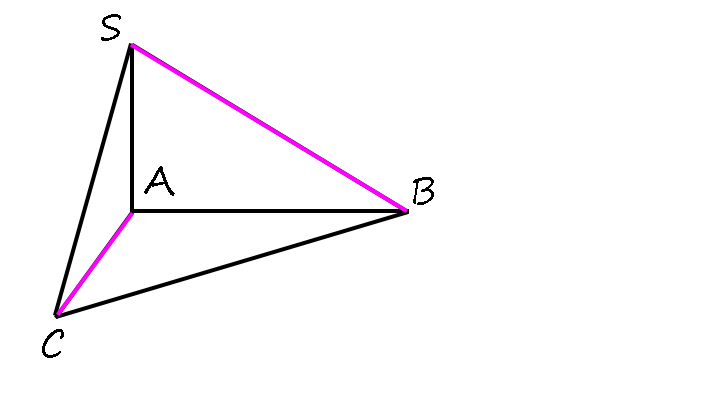
3) Дана пирамида SABC с высотой AS, в основании которой лежит прямоугольный треугольник с прямым углом A. Докажите, что SB⊥ AC.

Скажем, что BC — наклонная к плоскости (ABC):

1) SA ⊥ (ABC) => SA ⊥ AC
2) AB ⊥ AC ( ABC — прямоугольный треугольник по условию).

Вывод:

Два пункта доказательство и вывод!
1) Перпендикуляр будет опускаться на плоскость под 90 °.
2) Проекция наклонной на плоскость перпендикулярна прямой.
3) По т.т.п. наклонная перпендикулярна прямой.

Источник

Избранные теоремы геометрии тетраэдра (стр. 6 из 9)

Доказать, что скрещивающиеся ребра правильного тетраэдра взаимно перпендикулярны.

Пусть DH – высота правильного тетраэдра, точка H – центр правильного ΔABC. Тогда проекцией отрезка AD на плоскость основания ABC будет отрезок BH. Т.к. BH AC, то по теореме о трех перпендикулярах наклонная BD AC.

Дан правильный тетраэдр МАВС с ребром 1. найдите расстояние между прямыми AL и МО, где L-середина ребра МС, О-центр грани АВС.

Каждое ребро треугольной пирамиды PABCравно 1; BD– высота треугольника ABC. Равносторонний треугольник BDEлежит в плоскости, образующей угол ϕс ребром AC, причём точки Pи Eлежат по одну сторону от плоскости ABC. Найдите расстояние между точками Pи E.

Решение. Поскольку все рёбра пирамиды PABCравны, это правильный тетраэдр. Пусть M – центр основания ABC, N– ортогональная проекция вершины Eравностороннего треугольника BDEна плоскость ABC,K– середина BD,F– основание перпендикуляра, опущенного из точки Eна высоту PMтетраэдра PABC. Так какEK

Найди углы между скрещивающимися высотами соседних граней тетраэдра.

Пусть BK и DF – высоты граней ABC и BCD.

Запишем теорему косинусов для ΔDLF:

Случай №2 (высота расположена иначе).

BK и CN – высоты граней ABC и BCD. Проведем FP || CN и FL || BK.

Запишем теорему косинусов для ΔLFP:

Так как угол между прямыми по определению острый

Глава II. Тетраэдр в курсе математики средней школы

§1. Сравнительная характеристика изложения темы «тетраэдр» в школьных учебниках

Однако проблемы в изучении темы для учащихся существуют, и разные учебники пытаются решить их разными способами (порядком изложения теоретического материала, уровнем сложности задач и т.п.). Дадим краткую характеристику распространенных учебников геометрии в аспекте изучения тетраэдра.

Изложение темы «Тетраэдр» в учебнике «Геометрия» для 10-11 классов Атанасяна Л. С. и др.

В базовом учебнике «Геометрия» для 10-11 классов средней школы Атанасяна Л. С. и др. информацию о тетраэдре можно найти в 7 параграфах (12, 14, 28, 29, 32, 33, 69).

Источник

Пособие «Успешное решение стереометрической задачи»

Муниципальное общеобразовательное учреждение

«Новомичуринская средняя общеобразовательная школа №1»

Пронского района Рязанской области

Пособие по решению

(№14 ЕГЭ по математике)

Козлова Елена Александровна,

МОУ «Новомичуринская средняя

общеобразовательная школа № 1»

Угол между скрещивающимися прямыми …………………………………….

Площади сечений многогранников ……………………………………………

Расстояние от точки до плоскости …………………………………………….

Расстояние от точки до прямой ………………………………………………..

Угол между прямой и плоскостью ……………………………………………..

Расстояние между скрещивающимися прямыми ……………………………..

«Вдохновение есть расположение души к живейшему принятию впечатлений и соображению понятий, следственно и объяснению оных. Вдохновение нужно в геометрии, как и в поэзии».

Задание № 14 (С2) Единого государственного экзамена по математике представляет стереометрическую задачу. При решении такого вида задач используют поэтапно вычислительный или координатно-векторный методы.

В данном пособии даны рекомендации к решению и приведены решения некоторых задач именно поэтапно вычислительным методом (многие решения представлены учениками 10 – 11 классов 2012 – 2015 уч. г.). Этот метод является традиционным и требует от учащихся знание теории, практических умений и навыков, а также развитого пространственного воображения. В пособии много задач для самостоятельного решения, к которым даны ответы. Его можно использовать как на уроках геометрии, так и во внеурочное время для подготовки к ЕГЭ.

Желаю всем, кто увлечён геометрией, с вдохновением решать стереометрические задачи!

Угол между скрещивающимися прямыми

Определение. Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

Признак скрещивающихся прямых. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые являются скрещивающимися.

Определение. Углом между двумя пересекающимися прямыми называется наименьший из углов, образованных при пересечении прямых.

Величина угла между двумя пересекающимися прямыми принадлежит промежутку (0 0 ; 90 0 ).

Определение. Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся.

Полезно помнить следующие утверждения:

скрещивающиеся ребра правильной треугольной пирамиды взаимно перпендикулярны;

диагональ основания правильной четырехугольной пирамиды и скрещивающееся с ней боковое ребро взаимно перпендикулярны;

диагональ правильной четырехугольной призмы и скрещивающаяся с ней диагональ основания взаимно перпендикулярны.

Задачи для самостоятельного решения

В кубе АС ₁ точки Р и М – середины ребер А ₁ В ₁ и В ₁ С ₁ соответственно. Найдите косинус угла между прямыми АР и ВМ.

В правильной треугольной призме АВСА ₁ В ₁ С ₁ сторона основания равна 4, высота равна 10. Точки К и М – середины ребер АС и А ₁ В ₁ соответственно. Найдите косинус угла между прямыми АС ₁ и КМ.

Длины всех ребер правильной четырехугольной пирамиды РАВС D равны между собой. Найдите угол между прямыми РН и ВМ, если отрезок РН – высота данной пирамиды, точка М – середина её бокового ребра АР.

Пример 1. В правильной треугольной призме АВСА ₁ В ₁ С ₁ все ребра которой равны 1, найдите косинус угла между прямыми АВ ₁ и ВС ₁ .

Пример 2. В правильном тетраэдре АВС D найдите угол между высотой DH тетраэдра и медианой боковой грани BCD .

Решение Казаченко Виктории (11 класс, 2013 – 2014 уч. год).

Пример 4. В правильной треугольной призме АВСА ₁ В ₁ С ₁ сторона основания равна 4, высота равна 10. Точки К и М – середины ребер АС и А ₁ В ₁ соответственно. Найдите косинус угла между прямыми АС ₁ и КМ.

Решение Каковкиной Юлии (10 класс, 2014 – 2015 уч. год).

Площади сечений многогранников

Задачи для самостоятельного решения

Сторона основания правильной треугольной призмы АВСА ₁ В ₁ С ₁ равна 30. На ребрах АС, АВ и А ₁ В ₁ выбрали точки К, Р и М соответственно так, что АК : КС = АР : РВ = В ₁ М : МА ₁ = 2 : 1. Площадь сечения призмы плоскостью КРМ равна 210. Найдите площадь боковой грани данной призмы.

В правильной треугольной пирамиде МАВС с вершиной М высота равна 3, а боковые ребра равны 6. Найдите площадь сечения этой пирамиды плоскостью, проходящей через середины ребер АВ и АС параллельно прямой МА.

Площадь боковой поверхности правильной четырехугольной пирамиды SAB С D равна 108, а площадь полной поверхности этой пирамиды равна 144. Найдите площадь сечения, проходящего через вершину S этой пирамиды и через диагональ ее основания.

В правильной четырехугольной пирамиде МАВС D боковое ребро равно 8, высота пирамиды равна 2. Найдите площадь сечения, проходящего через прямую BD и середину F ребра МС.

Высота правильной четырехугольной пирамиды равна 80, сторона основания равна 120. Вычислить площадь сечения, проходящего через центр основания параллельно боковой грани.

В правильной четырехугольной пирамиде МАВС D с вершиной М стороны основания равны 3, а боковые ребра равны 8. Найдите площадь сечения пирамиды плоскостью, проходящей через точку В и середину ребра MD параллельно прямой АС.

В правильной пирамиде МАВС D АМ = 4, А D = 3. Постройте сечение пирамиды плоскостью, проходящей через диагональ В D основания параллельно ребру МА и найдите его площадь.

В правильной треугольной призме все ребра равны 1. Точка Е – середина ребра АС. Найдите площадь сечения призмы плоскостью А ₁ В ₁ Е.

Пример 1. Высота правильной треугольной пирамиды равна стороне ее основания, длина которого равна а . Найти площадь сечения пирамиды плоскостью, проходящей через сторону основания перпендикулярно противоположному ребру.

Пример 2. На ребре АВ прямоугольного параллелепипеда АС ₁ взята точка Е так, что АЕ : ЕВ = 4 : 1. Найдите площадь сечения плоскостью ЕСА ₁ , если АВ = 5, А D = 4, АА ₁ = 1.

Решение Перемыщевой Анны (10 класс, 2014 – 2015 уч. год).

Пример 3. Сторона основания правильной треугольной призмы АВСА ₁ В ₁ С ₁ равна 30. На ребрах АС, АВ и А ₁ В ₁ выбрали точки К, Р и М соответственно так, что АК : КС = АР : РВ = В ₁ М : МА ₁ = 2 : 1. Площадь сечения призмы плоскостью КРМ равна 210. Найдите площадь боковой грани данной призмы.

Решение Лутхова Андрея (10 класс, 2014 – 2015 уч. год).

Пример 4. Высота правильной четырехугольной пирамиды равна 80, сторона основания равна 120. Вычислить площадь сечения пирамиды плоскостью, проходящей через центр основания параллельно боковой грани.

Расстояние от точки до плоскости

Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.

Признак перпендикулярности двух плоскостей. Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

Признак параллельности прямой и плоскости. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

Признак параллельности двух плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

При решении задач по данной теме, применяют метод площадей, подобие треугольников, метод объемов.

Правила, которые помогут решить некоторые задачи.

Правило 1. Чтобы найти расстояние от данной точки до данной плоскости, достаточно найти расстояние от произвольной точки прямой, содержащей данную точку, до параллельной ей данной плоскости.

Правило 2. Чтобы найти расстояние от данной точки до данной плоскости, достаточно найти расстояние от произвольной точки плоскости, содержащей данную точку, до параллельной ей данной плоскости.

Необходимо знать, что:

в правильной треугольной пирамиде скрещивающиеся ребра взаимно перпендикулярны;

плоскость, проходящая через высоту правильной пирамиды (треугольной, четырехугольной, шестиугольной) и высоту её боковой грани (апофему), перпендикулярна этой боковой грани;

диагональ куба перпендикулярна плоскости, проведенной через концы трех ребер куба, выходящих из той же вершины, что и диагональ.

Задачи для самостоятельного решения

от центра основания пирамиды до грани EMD ;

В правильной четырехугольной пирамиде PABCD c основанием ABCD точка М – середина ребра РА, точка К – середина ребра РВ. Найдите расстояние от вершины А до плоскости СМК, если РС = 6, АВ = 4.

В правильной четырехугольной пирамиде М ABCD АР = 4, А D = 3. Постройте сечение пирамиды плоскостью, проходящей через диагональ В D основания параллельно ребру МА и найдите расстояние от точки М до плоскости сечения.

Ребро SA пирамиды SABC перпендикулярно плоскости основания АВС.

Постройте прямую пересечения плоскости, проходящей через середины ребер АВ, АС, S А, и плоскости, проходящей через середину ребра ВС и перпендикулярной ему.

Источник

Докажите что в правильном тетраэдре скрещивающиеся ребра взаимно перпендикулярны

Ребра тетраэдра равны 38. Найдите площадь сечения, проходящего через середины четырех его ребер.

В правильном тетраэдре скрещивающиеся ребра перпендикулярны. Каждая сторона сечения является средней линией соответствующей грани, и поэтому вдвое меньше параллельного ей ребра. Значит, сечением является квадрат со стороной 19. Тогда площадь сечения равна 361.

Ребра тетраэдра равны 32. Найдите площадь сечения, проходящего через середины четырех его ребер.

В правильном тетраэдре скрещивающиеся ребра перпендикулярны. Каждая сторона сечения является средней линией соответствующей грани, которая, как известно, в 2 раза меньше параллельной ей стороны и равна поэтому 16. Значит, сечением является квадрат со стороной 16. Тогда площадь сечения

Ребра тетраэдра равны 4. Найдите площадь сечения, проходящего через середины четырех его ребер.

Это задание ещё не решено, приводим решение прототипа.

Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер.

В правильном тетраэдре скрещивающиеся ребра перпендикулярны. Каждая сторона сечения является средней линией соответствующей грани, которая, как известно, в 2 раза меньше параллельной ей стороны и равна поэтому 0,5. Значит, сечением является квадрат со стороной 0,5. Тогда площадь сечения

Ребра тетраэдра равны 16. Найдите площадь сечения, проходящего через середины четырех его ребер.

Это задание ещё не решено, приводим решение прототипа.

Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер.

В правильном тетраэдре скрещивающиеся ребра перпендикулярны. Каждая сторона сечения является средней линией соответствующей грани, которая, как известно, в 2 раза меньше параллельной ей стороны и равна поэтому 0,5. Значит, сечением является квадрат со стороной 0,5. Тогда площадь сечения

Ребра тетраэдра равны 30. Найдите площадь сечения, проходящего через середины четырех его ребер.

Это задание ещё не решено, приводим решение прототипа.

Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер.

В правильном тетраэдре скрещивающиеся ребра перпендикулярны. Каждая сторона сечения является средней линией соответствующей грани, которая, как известно, в 2 раза меньше параллельной ей стороны и равна поэтому 0,5. Значит, сечением является квадрат со стороной 0,5. Тогда площадь сечения

Ребра тетраэдра равны 37. Найдите площадь сечения, проходящего через середины четырех его ребер.

Это задание ещё не решено, приводим решение прототипа.

Ребра тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер.

В правильном тетраэдре скрещивающиеся ребра перпендикулярны. Каждая сторона сечения является средней линией соответствующей грани, которая, как известно, в 2 раза меньше параллельной ей стороны и равна поэтому 0,5. Значит, сечением является квадрат со стороной 0,5. Тогда площадь сечения

Источник

Докажите что в правильном тетраэдре скрещивающиеся ребра взаимно перпендикулярны

На рёбрах AB и BC треугольной пирамиды ABCD отмечены точки M и N соответственно, причём AM : BM = CN : NB = 1 : 2. Точки P и Q — середины ребер DA и DC соответственно.

а) Докажите, что P, Q, M и N лежат в одной плоскости.

б) Найти отношение объёмов многогранников, на которые плоскость PQM разбивает пирамиду.

а) Треугольник ABC подобен треугольнику MBN по двум пропорциональным сторонам и углу между ними. Тогда углы BAC и BMN равны, и AC || MN. PQ || AC поскольку является средней линией треугольника ADC. Значит, MN || PQ и поэтому P, Q, M и N лежат в одной плоскости.

б) Пусть объём ABCD равен V. Пятигранник APMNCQ состоит из четырёхугольной пирамиды PACNM с основанием ACNM и треугольной пирамиды PQCN с основанием QCN. Выразим их объемы через V.

Расстояние от P до BCD вдвое меньше расстояния от A до BCD, а площади треугольников QCN и BCD, по теореме об отношении площадей треугольников с равным углом, относятся как 1 : 6. Значит,

Площадь треугольника MBN составляет площади ABC. Значит, Расстояние от точки P до ABC вдвое меньше расстояния от D до ABC, поэтому

Таким образом, то есть

Смею напомнить, что название пирамиды начинается с вершины, не лежащей на плоскости основания, а не как вздумается, из-за этого возникают серьезные проблемы при попытке решения.

Основанием данной треугольной пирамиды можно считать любую грань. И решение от этого не зависит.

Дана треугольная пирамида DABC, точки M, N, P и Q лежат на рёбрах AB, BC, AD, CD, причём AM : MB = CN : NB = 3 : 1. Точки P и Q — середины рёбер DA и DC соответственно.

а) Докажите, что точки P, Q, M и N лежат в одной плоскости.

б) Найдите отношение многоугольников на которые делит плоскость PQM пирамиду.

а) Треугольник ABC подобен треугольнику MBN по двум пропорциональным сторонам и углу между ними. Тогда углы BAC и BMN равны, и AC || MN. Далее, PQ || AC поскольку является средней линией треугольника ADC. Значит, MN || PQ и поэтому P, Q, M и N лежат в одной плоскости.

б) Пусть объём ABCD равен V. Пятигранник APMCQN состоит из четырёхугольной пирамиды PACNM с основанием ACNM и треугольной пирамиды PQCN с основанием QCN. Выразим их объемы через V.

Расстояние от P до (BCD) вдвое меньше расстояния от A до (BCD), а площади треугольников QCN и BCD относятся как 3 : 8. Значит,

Площадь треугольника MBN составляет площади ABC. Значит, Расстояние от точки P до (ABC) вдвое меньше расстояния от D до (ABC), поэтому

Таким образом, то есть

В правильной треугольной пирамиде SABC точки M, N и K — середины ребер основания, а P, Q и R делят боковые ребра SA, SB и SC в отношении 1 : 2, считая от вершины.

а) Доказать, что точки M, N, K, P, Q, R — лежат на одной сфере.

б) При каких углах наклона бокового ребра к основанию центр сферы лежит вне пирамиды SABC.

а) Поскольку прямая PQ параллельна прямой AB, прямая QR параллельна прямой BC, плоскости и параллельны. Пирамида тоже правильная, поэтому ее высота проходит через центр описанной окружности треугольника Она же является высотой пирамиды и проходит через центр вписанной окружности то есть центр описанной окружности

Таким образом, осталось найти на этой высоте точку так, чтобы такая точка и будет центром сферы. Заметим, что треугольники и подобны треугольнику с коэффициентами и соответственно, поэтому их радиусы описанных окружностей отличаются во столько же раз. Пусть тогда Пусть, далее, высота пирамиды равна Изобразим сечение пирамиды плоскостью Пусть, наконец, причем если лежит ниже мы считаем, что Тогда осталось приравнять расстояния. Имеем:

(это верно при любом положении точки );

Итак, мы доказали существование центра сферы.

б) Требуется, чтобы то есть

Ответ:

Источник