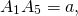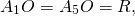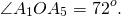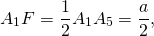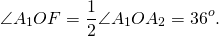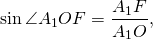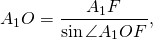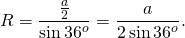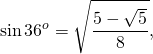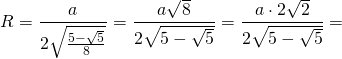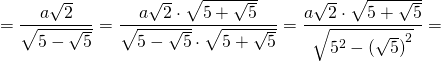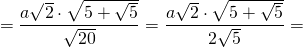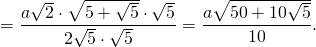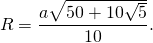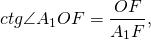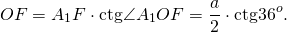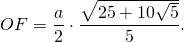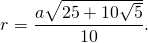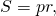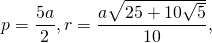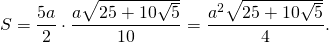Докажите что в правильном пятиугольнике диагонали равны
Правильный пятиугольник
По теореме о сумме углов выпуклого многоугольника, сумма углов правильного пятиугольника равна 180º(5-2)=540º.

Сумма внешних углов многоугольника, взятых по одному при каждой вершине, равна 360º. Поскольку все внешние углы правильного пятиугольника равны между собой, градусная мера каждого, например, угла 1, равна
∠1=360º:5=72º (можно было внешний угол искать как смежный с внутренним).
Каждый центральный угол правильного пятиугольника, например, угол A1O A2, равен
Как и любой другой правильный многоугольник, правильный пятиугольник вписан в окружность и описан около окружности.
Соединив центр правильного многоугольника с его вершинами, получим пять равных равнобедренных треугольников.
Основанием каждого такого треугольника равно стороне 5-угольника, боковые стороны равны радиусу описанной окружности, угол при вершине — центральному углу 5-угольника.

По свойству равнобедренного треугольника, OF является также медианой и биссектрисой треугольника A1OA5, то есть
Рассмотрим прямоугольный треугольник A1OF.
Таким образом, формула радиуса описанной около правильного пятиугольника окружности —
Подставив значение котангенса 36°, получаем:
Итак, формула радиуса вписанной в правильный пятиугольник окружности
можно найти площадь правильного пятиугольника. Здесь
Все диагонали правильного пятиугольника равны.
Доказательство равенства четырех диагоналей пятиугольника единице
1. Доказательство равенства четырех диагоналей пятиугольника единице
Определение 2.1.1. Диаметром d многоугольника М называется точная верхняя граница расстояний между его точками. [6, 68]
d=sup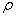
Х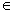
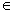
Теорема 2.1.1. Диаметр многоугольника равен расстоянию между некоторыми его вершинами.
Многоугольник М является ограниченной замкнутой областью. По теореме Вейерштрасса непрерывная функция 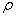
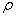
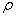
Х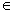
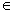
Отрезок АВ также будем называть диаметром многоугольника.
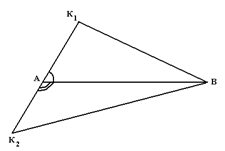
Ясно, что концы диаметра многоугольника должны находиться на его границе, при этом если хотя бы один из концов диаметра АВ не является вершиной многоугольника, то как видно из рисунка 2.1.1, один из отрезков K1B, K2B будет больше АВ (т.к. один из углов 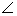
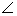
Итак, диаметр многоугольника совпадает либо с одной из сторон, либо с одной из диагоналей многоугольника.
Определение 2.1.2. Выпуклый многоугольник диаметра 1 будем называть оптимальным, если его периметр больше периметра любого другого выпуклого многоугольника диаметра 1.
Теорема 2.1.2. Все стороны оптимального пятиугольника меньше 1.
Для доказательства теоремы потребуется следующая лемма.
Лемма 2.1.1. Сумма расстояний от точки дуги окружности до ее концов принимает наибольшее значение, когда эта точка делит дугу пополам.
Пусть Р – точка дуги окружности, точки F и M ее концы (рис. 2.1.2).
Из 

FP+PM=2 r sin 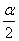
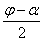
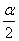
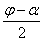
=2 r (2sin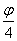
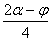
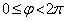
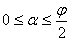
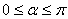
Сумма FP+PMпринимает наибольшее значение, когда cos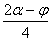
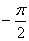
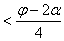
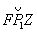
Таким образом, получаем: p 1 0 +1+ 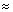
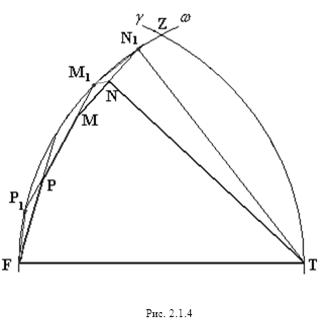
Рассмотрим второй случай, когда прямые PM, MN пересекают дугу окружности 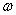
Из рисунка 2.1.4 видно, что периметр p рассматриваемого пятиугольника FPMNT меньше периметра P 2 пятиугольника FP1М1N1T т.е.:
p 2 3 правильного пятиугольника равен:
P 3 = 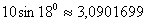
Таким образом, получаем, что периметр рассматриваемого пятиугольника FPMNT меньше периметра правильного пятиугольника диаметра 1.
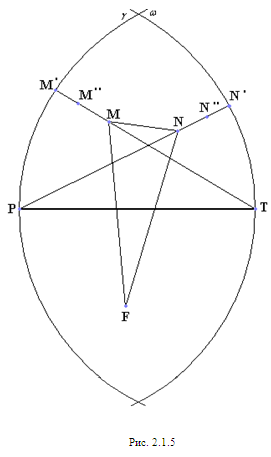
Теорема 2.1.3. В оптимальном пятиугольнике, по крайней мере, три диагонали равны 1.
Пусть диагональ PT=1 (по теореме 2.1.2).
Проведем две окружности: 
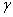
Рассмотрим первый случай, когда прямая MN пересекает дуги обеих окружностей