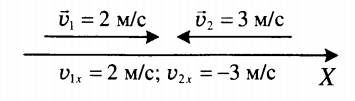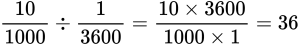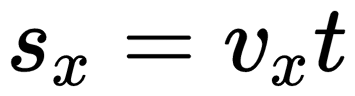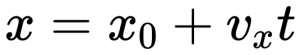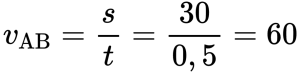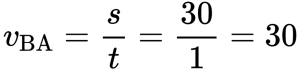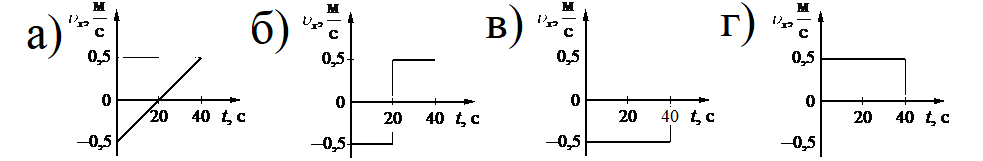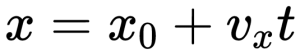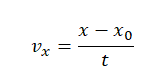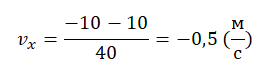Докажите что если времена движения на двух участках

18.12.202312.09.2023 admin 0 Comments

Средняя скорость (окончание)

7. Сравните промежутки времени, в течение которых Саша ехал и шёл пешком в первом и втором случаях.

Обобщим рассмотренные выше ситуации.

Рассмотрим сначала случай, когда тело двигалось с разными скоростями в течение равных промежутков времени.

Пусть первую половину всего времени движения тело двигалось со скоростью υ₁, а вторую половину — со скоростью υ₂. Можно ли найти среднюю скорость движения на всём участке, если не известны ни общее время движения, ни путь, пройденный телом за всё время движения?

Можно: для этого введём обозначения для всех нужных нам величин независимо от того, известны они или неизвестны. Это распространённый приём при решении многих задач.

Обозначим всё время движения t, весь путь l, а пути, пройденные за первую и вторую половину времени движения, обозначим соответственно l₁ и l₂.

8. Выразите через υ₁, υ₂ и t:

а) l₁ и l₂; б) l; в) среднюю скорость.

Найдя ответы на эти вопросы, вы узнаете, справедливо ли в общем случае утверждение: если тело двигалось на двух участках с разными скоростями в течение равных промежутков времени, то его средняя скорость на всём пути равна среднему арифметическому скоростей движения на двух участках.

Рассмотрим теперь случай, когда тело двигалось с разными скоростями первую и вторую половину пути.

Пусть теперь первую половину всего пути тело двигалось со скоростью υ₁ а вторую половину — со скоростью υ₂.

Обозначим снова всё время движения t, весь путь l, а промежутки времени, в течение которых тело двигалось на первом и втором участке, обозначим соответственно t₁ и t₂.

9. Выразите через υ₁, υ₂ и l:

a) t₁ и t₂; б) t; в) среднюю скорость.

Ответив на эти вопросы, вы узнаете, справедливо ли в общем случае утверждение: если тело двигалось на двух участках равной длины с разными скоростями, то его средняя скорость на всём пути не равна среднему арифметическому этих скоростей.

10. Докажите, что средняя скорость тела, которое двигалось на двух участках равной длины с разными скоростями, меньше, чем если бы оно двигалось на двух участках с теми же скоростями в течение равных промежутков времени.

Подсказка. Выразите для каждого из двух случаев среднюю скорость через скорости на первом и втором участках и сравните полученные выражения.

11. На первом участке пути тело двигалось со скоростью υ₁, а на втором — со скоростью υ₂. Чему равно отношение длин этих участков, если средняя скорость движения оказалась равной среднему арифметическому υ₁ и υ₂?

Источник

Мгновенная и средняя скорость

1. Мгновенная скорость

В этом параграфе мы будем рассматривать неравномерное движение. Однако при этом нам пригодится то, что мы знаем о прямолинейном равномерном движении.

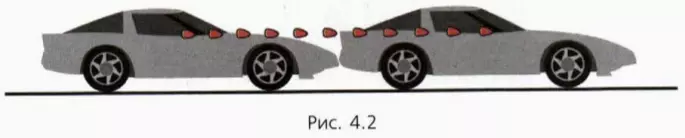
На рисунке 4.1 показаны положения разгоняющегося автомобиля на прямом шоссе с интервалом времени 1 с. Стрелка указывает на зеркальце заднего вида, положение которого мы рассмотрим далее более подробно.

Мы видим, что за равные интервалы времени автомобиль проходит разные пути, то есть движется неравномерно.

Уменьшим теперь последовательные интервалы времени в 20 раз – до 0,05 с – и проследим за изменением положения автомобиля в течение половины секунды (это нетрудно сделать, например, с помощью видеосъемки).

Чтобы не загромождать рисунок 4.2, на нем изображены только два положения автомобиля с промежутком времени 0,5 с. Последовательные положения автомобиля с интервалом 0,05 с отмечены положением его зеркальца заднего вида (показано красным цветом).

Мы видим, что когда последовательные равные промежутки времени достаточно малы, то пути, проходимые автомобилем за эти промежутки времени, практически одинаковы. А это означает, что движение автомобиля в течение столь малых промежутков времени можно с хорошей точностью считать прямолинейным равномерным.

Оказывается, этим замечательным свойством обладает любое движение (даже криволинейное): если рассматривать его за достаточно малый промежуток времени Δt, оно очень похоже на прямолинейное равномерное движение! Причем чем меньше промежуток времени, тем больше это сходство.

Скорость тела за достаточно малый промежуток времени и называют его скоростью в данный момент времени t, если этот момент времени находится в промежутке Δt. А более точное ее название – мгновенная скорость.

Насколько малым должен быть промежуток времени Δt, чтобы в течение этого промежутка движение тела можно было считать прямолинейным равномерным, зависит от характера движения тела.

В случае разгона автомобиля это доли секунды. А, например, движение Земли вокруг Солнца можно с хорошей точностью считать прямолинейным и равномерным даже в течение суток, хотя Земля за это время пролетает в космосе больше двух с половиной миллионов километров!

Говоря далее о скорости, мы будем (если это особо не оговорено) подразумевать обычно мгновенную скорость.

? 1. По рисунку 4.2 определите мгновенную скорость автомобиля. Длину автомобиля примите равной 5 м.

Значение мгновенной скорости автомобиля показывает спидометр (рис. 4.3).

Как найти мгновенную скорость по графику зависимости координаты от времени

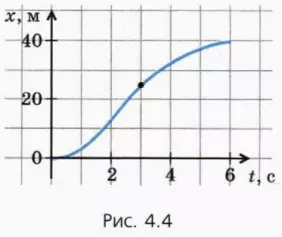
На рисунке 4.4 изображен график зависимости координаты от времени для автомобиля, который движется по прямолинейному шоссе.

Мы видим, что он движется неравномерно, потому что график зависимости его координаты от времени – это кривая, а не отрезок прямой.

Покажем, как определить по этому графику мгновенную скорость автомобиля в какой-либо момент времени – скажем, при t = 3 с (точка на графике).

Для этого рассмотрим движение автомобиля за столь малый промежуток времени, в течение которого его движение можно считать прямолинейным равномерным.

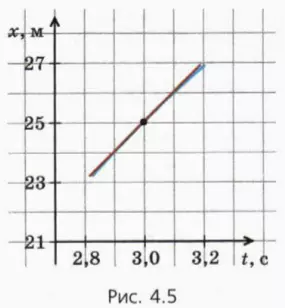
На рисунке 4.5 показан интересующий нас участок графика при десятикратном увеличении (см., например, шкалу времени).

Мы видим, что этот участок графика практически неотличим от отрезка прямой (красный отрезок). За последовательные равные промежутки времени по 0,1 с автомобиль проходит практически одинаковые расстояния – по 1 м.

2. Чему равна мгновенная скорость автомобиля в момент t = 3 с?

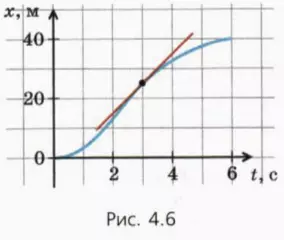
Возвращаясь к прежнему масштабу чертежа, мы увидим, что прямая красного цвета, с которой практически совпадал малый участок графика, – касательная к графику зависимости координаты от времени в данный момент времени (рис. 4.6).

Итак, о мгновенной скорости тела можно судить по угловому коэффициенту касательной к графику зависимости координаты от времени: чем больше угловой коэффициент касательной, тем больше скорость тела. (Описанный способ определения мгновенной скорости с помощью касательной к графику зависимости координаты от времени связан с понятием производной функции. Это понятие вы будете изучать в курсе «Алгебра и начала аиализа».) А в тех точках графика, где угол наклона касательной равен нулю, то есть касательная параллельна оси времени t, мгновенная скорость тела равна нулю.

? 3. Рассмотрите рисунок 4.6.
а) В каких точках графика угол наклона касательной наибольший? наименьший?
б) Найдите наибольшую и наименьшую мгновенную скорость автомобиля в течение первых 6 с его движения.

2. Средняя скорость

Во многих задачах используют среднюю скорость, связанную с пройденным путем:

Определенная таким образом средняя скорость является скалярной величиной, так как путь – это скалярная величина. (Иногда во избежание недоразумений ее называют средней путевой скоростью.)

Например, если автомобиль в течение трех часов проехал по городу 120 км (при этом он мог разгоняться, тормозить и стоять на перекрестках), то его средняя скорость равна 40 км/ч.

? 4. Насколько уменьшится средняя скорость только что упомянутого автомобиля, если из-за остановок в пробках общее время движения увеличится на 1 ч?

Средняя скорость на двух участках движения

Во многих задачах рассматривается движение тела на двух участках, на каждом из которых движение можно считать равномерным. В таком случае, согласно определению средней скорости (1), можно записать:

где l₁ и t₁ – путь и время для первого участка, а l₂ и t₂ – для второго. Рассмотрим примеры.
Саша выехал из поселка на велосипеде со скоростью 15 км/ч и ехал в течение часа. А потом велосипед сломался, и Саша еще час шел пешком со скоростью 5 км/ч.

? 5. Найдите:
а) путь, пройденный Сашей за все время движения;
б) общее время движения Саши;
в) среднюю скорость Саши.

В рассмотренном случае средняя скорость оказалась равной среднему арифметическому скоростей, с которыми Саша ехал и шел. Всегда ли это справедливо? Рассмотрим следующий пример.
Пусть Саша ехал на велосипеде в течение часа со скоростью 15 км/ч, а потом прошел такое же расстояние пешком со скоростью 5 км/ч.

? 6. Найдите:
а) путь, который Саша прошел пешком;
б) путь, пройденный Сашей за все время движения;
в) общее время движения Саши;
б) среднюю скорость Саши.

Рассмотрев этот случай, вы увидите, что на этот раз средняя скорость не равна среднему арифметическому скоростей езды и ходьбы. А если присмотреться еще внимательнее, то можно заметить, что во втором случае средняя скорость меньше, чем в первом. Почему?

? 7. Сравните промежутки времени, в течение которых Саша ехал и шел пешком в первом и втором случаях.

Обобщим рассмотренные выше ситуации.

Рассмотрим сначала случай, когда тело двигалось с разными скоростями в течение равных промежутков времени.

Пусть первую половину всего времени движения тело двигалось со скоростью v₁, а вторую половину – со скоростью v₂. Можно ли найти среднюю скорость движения на всем участке, если не известны ни общее время движения, ни путь, пройденный телом за все время движения?

Можно: для этого введем обозначения для всех нужных нам величин независимо от того, известны они или неизвестны. Это распространенный прием при решении многих задач.

Обозначим все время движения t, весь путь l, а пути, пройденные за первую и вторую половину времени движения, обозначим соответственно) l₁ и l₂.

? 8. Выразите через v₁, v₂ и t:
a) l₁ и l₂; б) l; в) среднюю скорость.

Найдя ответы на эти вопросы, вы узнаете, справедливо ли в общем случае утверждение: если тело двигалось на двух участках с разными скоростями в течение равных промежутков времени, то его средняя скорость на всем пути равна среднему арифметическому скоростей движения на двух участках.

Рассмотрим теперь случай, когда тело двигалось с разными скоростями первую и вторую половину пути.

Пусть теперь первую половину всего пути тело двигалось со скоростью v₁, а вторую половину – со скоростью v₂. Обозначим снова все время движения t, весь путь l, а промежутки времени, в течение которых тело двигалось на первом и втором участке, обозначим соответственно t₁ и t₂.

? 9. Выразите через v₁, v₂ и l:
а) t₁ и t₂; б) t; в) среднюю скорость.

Ответив на эти вопросы, вы узнаете, справедливо ли в общем случае утверждение: если тело двигалось на двух участках равной длины с разными скоростями, то его средняя скорость на всем пути не равна среднему арифметическому этих скоростей.

? 10. Докажите, что средняя скорость тела, которое двигалось на двух участках равной длины с разными скоростями, меньше, чем если бы оно двигалось на двух участках с теми же скоростями в течение равных промежутков времени.
Подсказка. Выразите для каждого из двух случаев среднюю скорость через скорости на первом и втором участках и сравните полученные выражения.

? 11. На первом участке пути тело двигалось со скоростью v₁, а на втором – со скоростью v₂. Чему равно отношение длин этих участков, если средняя скорость движения оказалась равной среднему арифметическому v₁ и v₂?

Дополнительные вопросы и задания

12. Одну треть всего времени движения поезд ехал со скоростью v₁, а оставшееся время – со скоростью v₂.
а) Выразите пройденный поездом путь через v₁, v₂ и все время движения t.
б) Выразите среднюю скорость поезда через v₁ и v₂.
в) Найдите числовое значение средней скорости при v₁ = 60 км/ч, v₂ = 90 км/ч.

13. Автомобиль ехал три четверти всего пути со скоростью v₁, а оставшийся участок пути – со скоростью v₂.
а) Выразите все время движения автомобиля через v₁, v₂ и весь пройденный путь l.
б) Выразите среднюю скорость движения автомобиля через v₁ и v₂.
в) Найдите числовое значение средней скорости при v₁ = 80 км/ч, v₂ = 100 км/ч.

14. Автомобиль ехал 2 ч со скоростью 60 км/ч. Сколько времени после этого он должен ехать со скоростью 80 км/ч, чтобы его средняя скорость на всем пути стала равной 66,7 км/ч?

15. Перенесите в тетрадь (по клеточкам) график зависимости координаты автомобиля от времени, изображенный на рисунке 4.4. Считайте, что автомобиль едет вдоль оси x.
а) Определите графически среднюю скорость за 6 с.
б) Используя касательную, определите, в какие примерно моменты времени мгновенная скорость автомобиля была равна его средней скорости за 6 с.

Источник

Равномерное прямолинейное движение

теория по физике 🧲 кинематика

Равномерное прямолинейное движение — это такое движение, при котором тело совершает за любые равные промежутки времени равные перемещения.

Скорость при прямолинейном равномерном движении

Если тело движется равномерно и прямолинейно, его скорость остается постоянной как по модулю, так и по направлению. Ускорение при этом равно нулю.

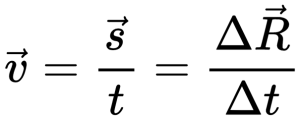
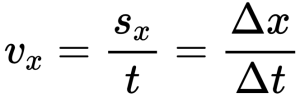
Векторный способ записи скорости при равномерном прямолинейном движении:s — вектор перемещения, ΔR— изменение радиус-вектора, t — время, а ∆t — его изменение. Проекция скорости на ось ОХ: s_x — проекция перемещения на ось ОХ, ∆x — изменение координаты точки (ее абсциссы). Знак модуля скорости зависит от направления вектора скорости и оси координат:

Основная единица измерения скорости — 1 метр в секунду. Сокращенно — 1 м/с.

Спидометр — прибор для измерения модули скорости тела.

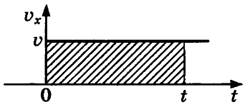
График зависимости скорости от времени представляет собой прямую линию, перпендикулярную оси скорости и параллельную оси времени. Выглядит он так:

Чтобы сравнить модули скоростей на графике, нужно оценить их удаленность от оси времени. Чем дальше график от оси, тем больше модуль.

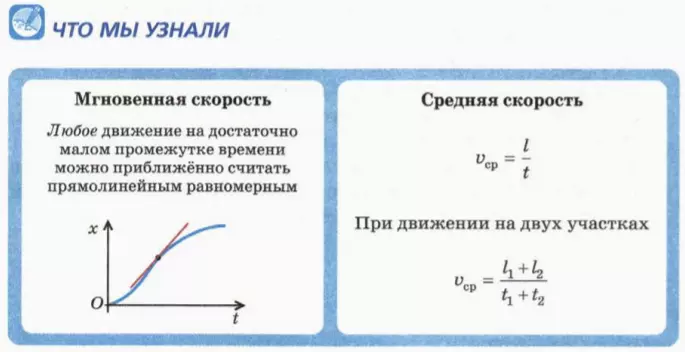
Пример №1. Найти модуль скорости и направление движения тела относительно оси ОХ. Выразить скорость в км/ч.

График скорости пересекает ось в точке со значением 10. Единица измерения — м/с. Поэтому модуль скорости равен 10 м/с. График лежит выше оси времени. Это значит, что тело движется по направлению оси ОХ. Чтобы выразить скорость в км/ч, нужно перевести 10 м в километры и 1 с в часы:

Теперь нужно разделить километры на часы:

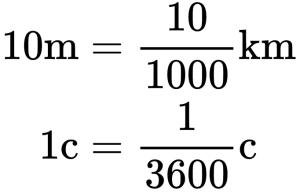
Перемещение и координаты тела при равномерном прямолинейном движении

Геометрический смысл перемещения заключается в том, что его модуль равен площади фигуры, ограниченной графиком скорости, осями скорости и времени, а также линией, проведенной перпендикулярно оси времени.

При прямолинейном равномерном движении эта фигура представляет собой прямоугольник. Поэтому модуль перемещения вычисляется по следующей формуле:

Вектор перемещения равен произведению вектора скорости на время движения: Внимание!

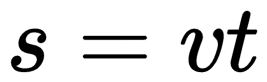
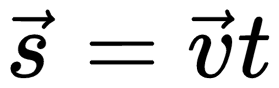
При равномерном прямолинейном движении путь и перемещение совпадают. Поэтому путь, пройденный телом, можно найти по этим же формулам.

Формула проекции перемещения:

График проекции перемещения

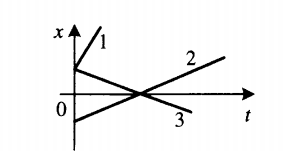
График проекции перемещения показывает зависимость этой проекции от времени. При прямолинейном равномерном движении он представляет собой луч, исходящий из начала координат. Выглядит он так:

Чтобы по графику проекции перемещения сравнить модули скоростей, нужно сравнить углы их наклона к оси s_x.Чем меньше угол, тем больше модуль. Согласно рисунку выше, модули скорости тел, которым соответствуют графики 1 и 3, равны. Они превосходят модуль скорости тела 2, так как их угол наклона к оси s_x меньше.

График координаты

График координаты представляет собой график зависимости координаты от времени. Выглядит он так:

Так как график координаты представляет собой график линейной функции, уравнение координаты принимает вид :

Чтобы сравнить модули скоростей тел по графику координат, нужно сравнить углы наклона графика к оси координат. Чем меньше угол, тем больше модуль скорости. На картинке выше наибольший модуль скорости соответствует графику 1. У графиков 2 и 3 модули равны.

Чтобы по графику координат найти время встречи двух тел, нужно из точки пересечения их графиков провести перпендикуляр к оси времени.

Пример №2. График зависимости координаты тела от времени имеет вид:

Изучите график и на его основании выберите два верных утверждения:

На участке 1 координата растет, и ее график представляет собой прямую. Это значит, что на этом участке тело движется равномерно (с постоянной скоростью). На участке 2 координата с течением времени не меняется, что говорит о том, что тело покоится. Исходя из этого, верными утверждениями являются номера 1 и 3.

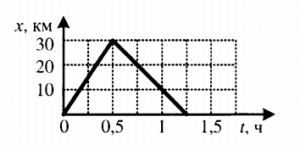
Пример №3. На рисунке изображен график движения автомобиля из пункта А (х=0 км) в пункт В (х=30 км). Чему равна минимальная скорость автомобиля на всем пути движения туда и обратно?

Согласно графику, с начала движения до прибытия автомобиля в пункт 2 прошло 0,5 часа. А с начала движения до возвращения в пункт А прошло 1,5 часа. Поэтому время, в течение которого тело возвращалось из пункта В в пункт А, равно:

Туда и обратно автомобиль проходил равные пути, каждый из которых равен 30 км. Поэтому скорость во время движения от А к В равна:

Скорость во время движения от В к А равна:

Минимальная скорость автомобиля на всем пути движения составляет 30 км/ч.

На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Скорость второго тела v₂ больше скорости первого тела v₁ в n раз, где n равно…