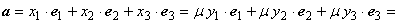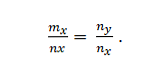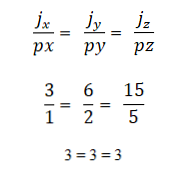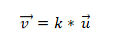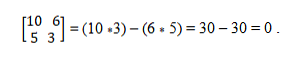Докажите что если два вектора коллинеарны то координаты одного вектора пропорциональны координатам
Условие коллинеарности векторов
В статье ниже рассмотрим условия, при которых векторы считаются коллинеарными, а также разберем тему на конкретных примерах. И, прежде чем приступить к обсуждению, напомним некоторые определения.
Коллинеарные векторы – ненулевые векторы, лежащие на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому.
Данное определение дает возможность убедиться в коллинеарности векторов в их геометрическом отображении, однако точность такого способа может иметь погрешности, например, в зависимости, от качества самого чертежа. Поэтому обратимся к алгебраическому толкованию: сформируем условие, которое будет явным признаком коллинеарности.
Координатная форма условия коллинеарности векторов
Мы можем также получить еще одно условие коллинеарности векторов, опираясь на понятие их произведения.
Два ненулевых вектора коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.
Рассмотрим применение условия коллинеарности на конкретных примерах.
Решение
Ответ: заданные векторы коллинеарны.
Решение
Решение
Согласно выведенному выше условию, векторы коллинеарны, если
b → = λ · a → ⇔ b x = λ · a x b y = λ · a y ⇔ p = λ · 2 3 = λ · 7
Ответ: при p = 6 7 заданные векторы коллинеарны.
Также распространены задачи на нахождения вектора, коллинеарного заданному. Решаются они без затруднений, основываясь на условии коллинеарности: : достаточным будет взять произвольное действительное число λ и определить вектор, коллинеарный данному.
Решение
Решение
Коллинеарность векторов, условия коллинеарности векторов.
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 1).
 |
| рис. 1 |
Условия коллинеарности векторов
Два вектора будут коллинеарны при выполнении любого из этих условий:
Условие коллинеарности векторов 1. Два вектора a и b коллинеарны, если существует число n такое, что
N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю.
N.B. Условие 3 применимо только для трехмерных (пространственных) задач.
Доказательство третего условия коллинеарности
Пусть есть два коллинеарные вектора a = < ax ; ay ; az > и b = < nax ; nay ; naz >. Найдем их векторное произведение
Примеры задач на коллинеарность векторов
Примеры задач на коллинеарность векторов на плоскости
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае плоской задачи для векторов a и b примет вид:
| ax | = | ay | . |
| bx | by |
| Вектора a и b коллинеарны т.к. | 1 | = | 2 | . |
| 4 | 8 |
| Вектора a и с не коллинеарны т.к. | 1 | ≠ | 2 | . |
| 5 | 9 |
| Вектора с и b не коллинеарны т.к. | 5 | ≠ | 9 | . |
| 4 | 8 |
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение n a :
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | . |
| bx | by |
Решим это уравнение:
Ответ: вектора a и b коллинеарны при n = 6.
Примеры задач на коллинеарность векторов в пространстве
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности, которое в случае пространственной задачи для векторов a и b примет вид:
| ax | = | ay | = | az | . |
| bx | by | bz |
Вектора a и b коллинеарны т.к. 1 4 = 2 8 = 3 12
Вектора a и с не коллинеарны т.к. 1 5 = 2 10 ≠ 3 12
Вектора с и b не коллинеарны т.к. 5 4 = 10 8 ≠ 12 12
Решение: Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием коллинеарности, найдем существует ли такое число n при котором:
| n = | by | = | 6 | = 2 |
| ay | 3 |
Найдем значение n a :
Решение: Так как вектора не содержат компоненты равные нулю, то воспользуемся вторым условием коллинеарности
| ax | = | ay | = | az | . |
| bx | by | bz |
Из этого соотношения получим два уравнения:
| 3 | = | 2 |
| 9 | n |
| 3 | = | m |
| 9 | 12 |
Решим эти уравнения:
| n = | 2 · 9 | = 6 |
| 3 |
| m = | 3 · 12 | = 4 |
| 9 |
Ответ: вектора a и b коллинеарны при n = 6 и m = 4.
Коллинеарные векторы
В данной публикации мы рассмотрим, какие векторы называются коллинеарными и перечислим условия, при которых они являются таковыми. Также разберем примеры решения задач по этой теме.
Условия коллинеарности векторов
Векторы, лежащие на одной или нескольких параллельных прямых, называются коллинеарными.
Два вектора коллинеарны, если выполняется одно из условий ниже:
2. Отношения координат векторов равны. Но данное условие не может применяться, если одна из координат равняется нулю.
3. Векторное произведение равно нулевому вектору (применимо только для трехмерных задач).
Примеры задач
Решение:
У заданных векторов нет нулевых координат, значит мы можем применить второе условие коллинеарности.
Задание 2
Выясним, при каком значении n векторы и коллинеарны.
Решение:
Т.к. среди координат нет нулей, согласно второму условию мы можем составить их соотношение, чтобы рассчитать недостающий элемент.
1.5.2. Линейные операции в координатной форме.
Рассмотрим, как преобразуются координаты при сложении векторов и при умножении вектора на число.
Теорема 1.5.2. При сложении векторов их соответствующие координаты складываются.
Док-во. Пусть 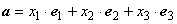
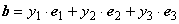
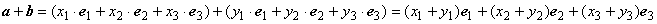
Теорема 1.5.3. При умножении вектора на число все его координаты умножаются на это число.
Док-во. Пусть 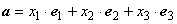
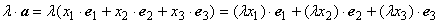
При доказательстве обеих теорем используются свойства операций сложения векторов и умножения вектора на число, входящие в определение векторного пространства.
Следствие из теор. 1.5.3: Критерий коллинеарности векторов. Два ненулевых вектора коллинеарны тогда и только тогда, когда их координаты в любом базисе пропорциональны.
Док-во. Необходимость. Пусть векторы а(х1, х2, х3) и b(y1, y2, y3) коллинеарны. Тогда по теореме 1.4.6. 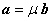
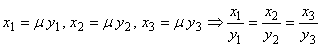
Достаточность. Если координаты векторов пропорциональны, т.е. 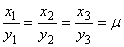
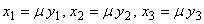
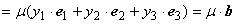
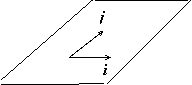
Опр.1.5.4. Базис векторного пространства называется ортонормированным, если составляющие его векторы взаимно перпендикулярны и имеют единичную длину.
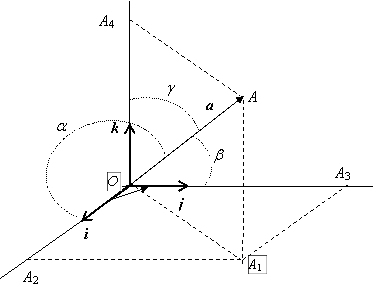
Опр. 1.5.5. Упорядоченная тройка некомпланарных векторов a, b, c называется правой, если при приведении этих векторов к общему началу кратчайший поворот от a к b виден из конца вектора c против часовой стрелки (если кратчайший поворот от a к b совершается по часовой стрелке, то тройка векторов a, b, c называется левой).
Заметим, что если тройка a, b, c – правая (левая), то правыми (левыми) являются тройки b, c, a и c, a, b, т.е. ориентация не меняется при циклической перестановке векторов. В тоже время перестановка двух векторов меняет ориентацию: если тройка a, b, c – правая (левая), то тройка b, a, c (и, как следствие, тройки a, c, b и c, b, a) – левая (правая).
Ортонормированный базис в пространстве будем задавать правой тройкой ортов i, j, k. Произвольный вектор пространства a теперь может быть представлен в виде 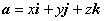
Чтобы распечатать файл, скачайте его (в формате Word).
Коллинеарная система и примеры
коллинеарные векторы Они являются одним из трех типов существующих векторов. Речь идет о тех векторах, которые находятся в одном направлении или направлении действия. Это означает следующее: два или более векторов будут коллинеарными, если они расположены в виде прямых линий, параллельных друг другу.
Вектор определяется как величина, применяемая к телу, и характеризуется как имеющий направление, смысл и масштаб. Векторы могут быть найдены в плоскости или в пространстве и могут быть разных типов: коллинеарные векторы, параллельные векторы и параллельные векторы.
Коллинеарные векторы
Векторы коллинеарны, если линия действия одного является точно такой же линией действия всех других векторов, независимо от размера и смысла каждого из векторов..
Векторы используются в качестве представлений в различных областях, таких как математика, физика, алгебра, а также в геометрии, где векторы коллинеарны только тогда, когда их направление одинаково, независимо от того, имеет ли их значение значение.
черты
— Два или более вектора коллинеарны, если соотношение между координатами равно.
Пример 1
У нас есть векторы m = m_x; m_y и n = n_x; n_y. Они коллинеарны, если:
Пример 2
— Два или более векторов коллинеарны, если произведение или вектор умножения равен нулю (0). Это связано с тем, что в системе координат каждый вектор характеризуется своими соответствующими координатами, и если они пропорциональны друг другу, векторы будут коллинеарными. Это выражается следующим образом:
Пример 1
У нас есть векторы a = (10, 5) и b = (6, 3). Чтобы определить, являются ли они коллинеарными, применяется теория детерминантов, которая устанавливает равенство перекрестных произведений. Таким образом, вы должны:
Коллинеарная векторная система
Коллинеарные векторы представлены графически с использованием направления и смысла их, учитывая, что они должны проходить через точку приложения и модуль, который имеет определенный масштаб или длину.
Система коллинеарных векторов формируется, когда два или более векторов воздействуют на объект или тело, представляя силу и действуя в одном направлении..
Например, если к телу приложены две коллинеарные силы, их результат будет зависеть только от направления, в котором они действуют. Есть три случая, которые:
Коллинеарные векторы с противоположными чувствами
Результирующий из двух коллинеарных векторов равен сумме этих:
пример
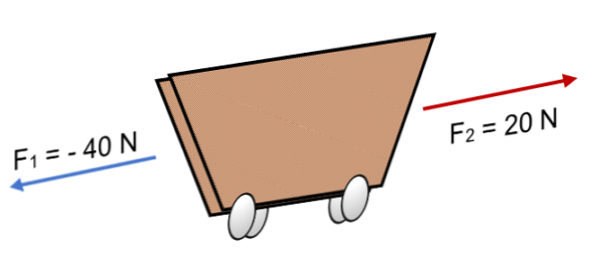
Если на тележку F действуют две силы1 = 40 Н и F2 = 20 Н в обратном направлении (как показано на рисунке), результат:
R = Σ F = (- 40 Н) + 20 Н.
Коллинеарные векторы с одинаковым смыслом
Величина результирующей силы будет равна сумме коллинеарных векторов:
пример
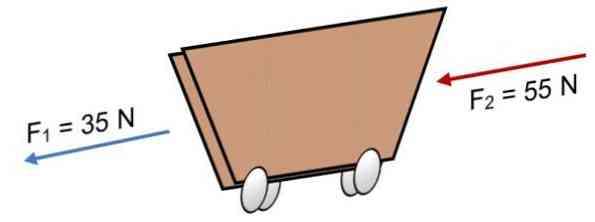
Если на тележку F действуют две силы1 = 35 Н и F2 = 55 Н в том же направлении (как показано на рисунке), результат:
R = Σ F = 35 Н + 55 Н.
Положительный результат показывает, что коллинеарные векторы действуют влево.
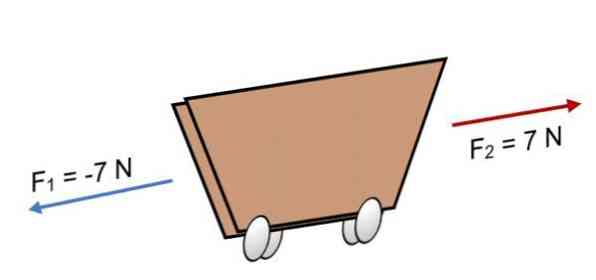
Коллинеарные векторы с одинаковыми величинами и противоположными значениями
Результирующий из двух коллинеарных векторов будет равен сумме коллинеарных векторов:
Поскольку силы имеют одинаковую величину, но в противоположном направлении, то есть одно будет положительным, а другое отрицательным, при сложении двух сил результирующее значение будет равно нулю.
пример
Поскольку результат равен 0, это означает, что векторы сбалансированы друг с другом и, следовательно, тело находится в равновесии или в состоянии покоя (оно не будет двигаться).
Разница между коллинеарным и параллельным векторами
Коллинеарные векторы характеризуются наличием одинакового направления на одной линии или потому, что они параллельны линии; то есть они являются векторами прямых параллельных линий.
С другой стороны, параллельные векторы определены, потому что они находятся в разных направлениях действия, которые перехвачены в одной точке.
Системы параллельных векторов решаются математическими методами или графами, которые являются методом параллелограмма сил и методом многоугольника сил. По ним будет определяться значение результирующего вектора, который указывает направление, в котором будет двигаться тело..
По сути, основное различие между коллинеарными векторами и параллельными векторами заключается в линии действия, в которой они действуют: коллинеарные действуют в одной линии, тогда как параллельные в разных.
То есть коллинеарные векторы действуют в одной плоскости: «X» или «Y»; и одновременный акт в обеих плоскостях, начиная с одной и той же точки.
Коллинеарные векторы не находятся в одной точке, как параллельные, потому что они параллельны друг другу.
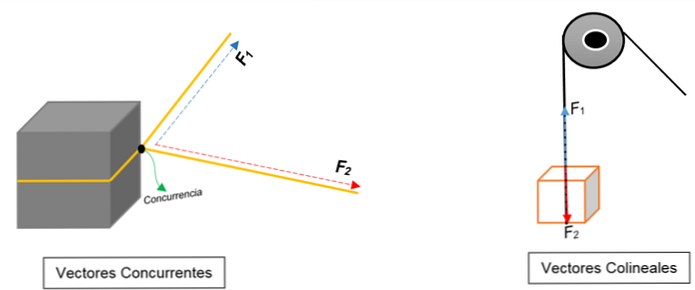
На левом изображении вы можете увидеть блок. Он связан веревкой, а узел делит его на две части; когда тянуть в разные стороны и с разными силами, блок будет двигаться в том же направлении.
Представлены два вектора, которые совпадают в точке (блоке), независимо от их модуля, смысла или направления.
Вместо этого на правом изображении появляется шкив, который поднимает коробку. Веревка представляет собой линию действий; когда его тянут, на него действуют две силы (векторы): одна сила натяжения (при подъеме на блок) и другая сила, та, которая воздействует на вес блока. Оба имеют одинаковое направление, но в противоположных направлениях; не соглашайтесь в точке.