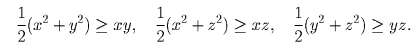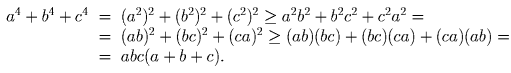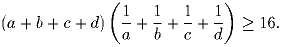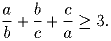Докажите что если a b c 0 то a3 b3 c3 3abc
докажите, что a^3+b^3+c^3=3abc, если a+b+c=0
a^3 это а в степени 3
Другие вопросы из категории
включили мотор и через один час после этого прибыли к месту старта. Во сколько раз скорость течения реки меньше собвственной скорости лодки? Скорость лодки в неповдижной воде(собвстенная скорость лодки) и скорость течения реки считаются постоянными.
Читайте также
есть число рациональное.
2. Докажите, что значение выражения есть число рациональное.
2) Докажите, что выражение А*В-С*D тождественно равно выражению С*D-A*B, если А=ах, В=су-b, C=x и D=acy-ab.
-биссектриса угла CAD.№2. Прямоугольные треугольники АВС и АВD имеют общую гипотенузу АВ. Известно, что AC=BD. Докажите, что AD параллельна ВС.№3. Прямоугольные треугольники АВС и АВD имеют общую гипотенузу АВ.(катеты СВ и DА пересекаются в точке О). Известно, что угол СВА равен углу DАВ. Докажите равенство треугольников АСО и ВDО
2)Докажите что при любом целом y значение выражения 32у+(у-8)^-y(y-16) кратно 32
прямых секущей соответственные углы равны,то прямые параллейны.
3.докажите,что если при пересечении 2 прямых секущей сумма односторонних углов равна 180 градусам,то прямые параллейны.
4.объясните,какие утвержения называются аксиомами.приведите примеры аксиом
Докажите что если a b c 0 то a3 b3 c3 3abc
Задача 17:
Докажите, что 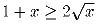
Решение:
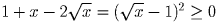
Задача 18:
Докажите, что x + 1/x ≥ 2 при x > 0.
Решение:
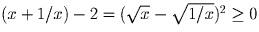
Задача 19:
Докажите, что (x² + y²)/2 ≥ xy при любых x и y.
Решение:
Перегруппировав члены, получаем (x – y)² ≥ 0.
Задача 20:
Докажите, что 2(x² + y²) ≥ (x + y)² при любых x и y.
Решение:
Перегруппировав члены, получаем (x – y)² ≥ 0.
Задача 21:
Докажите, что 1/x + 1/y ≥ 4/(x + y) при x,y > 0.
Решение:
Приводим к общему знаменателю и получаем (x – y)² ≥ 0.
Задача 22:
Докажите, что x² + y² + z² ≥ xy + yz + zx при любых x, y, z.
Решение:
Запишем три неравенства:
Сложив их, мы и получим требуемое неравенство.
Задача 23:
a, b, c ≥ 0. Докажите, что (a + b)(a + c)(b + c) ≥ 8abc.
Решение:
Надо перемножить три неравенства: 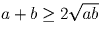
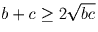
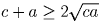
Задача 24:
a, b, c ≥ 0. Докажите, что 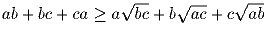
Решение:
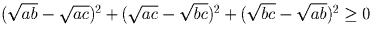
Задача 25:
Докажите, что x² + y² + 1 ≥ xy + x + y при любых x и y.
Решение:
x² + y² + 1 – xy – x – y = ((x – y)² + (x – 1)² + (y – 1)²)/2 ≥ 0.
Задача 26:
Докажите, что при любых a, b, c имеет место неравенство: a 4 + b 4 + c 4 ≥ abc(a + b + c).
Решение:
Воспользуемся неравенством x² + y² + z² ≥ xy + yz + zx, причем дважды:
Задача 27:
Докажите, что x 4 + y 4 + 8 ≥ 8xy при любых x и y.
Решение:
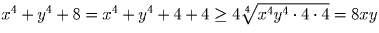
Задача 28:
a, b, c, d – положительные числа. Докажите, что
Решение:
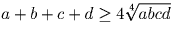
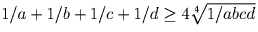
Задача 29:
a, b, c – положительные числа. Докажите, что
Решение:
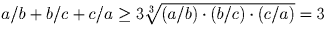
Задача 30:
Докажите, что при x ≥ 0 имеет место неравенство 3x³ – 6x² + 4 ≥ 0.
Решение:
Докажем, что 3x³ + 4 ≥ 6x². Но 3x³ + 4 = 2x³ + x³ + 4. Применяя неравенство Коши, получаем
Задача 31:
Докажите, что при a, b, c > 0 имеет место неравенство 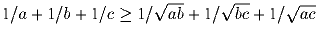
Задача 32:
Докажите, что при a, b, c > 0 имеет место неравенство ab/c + ac/b + bc/a ≥ a + b + c.
Задача 33:
Докажите, что при a, b, c ≥ 0 имеет место неравенство ((a + b + c)/3)² ≥ (ab + bc + ca)/3.
Задача 34:
Докажите, что при a, b, c ≥ 0 имеет место неравенство (ab + bc + ca)² ≥ 3abc(a + b + c).
Задача 35:
Сумма трех положительных чисел равна шести. Докажите, что сумма их квадратов не меньше 12.
Задача 36:
Докажите, что при x ≥ 0 имеет место неравенство 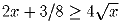
Задача 37:
Сумма двух неотрицательных чисел равна 10. Какое максимальное и какое минимальное значение может принимать сумма их квадратов?
Задача 38:
Докажите неравенство Коши для пяти чисел, т.е. докажите, что при a, b, c, d, e ≥ 0 имеет место неравенство
Решение:
Указание. Докажите сначала неравенство Коши для восьми чисел, а затем воспользуйтесь той же идеей, что и при доказательстве неравенства Коши для трех чисел.