До замыкания рубильника амперметр показывал 2 а что он покажет после замыкания

Расчет электрических цепей постоянного тока. Расчет электрических цепей при периодических несинусоидальных ЭДС, токах и напряжениях

Страницы работы

Фрагмент текста работы

Цель занятия – приобрести навыки расчета и анализа цепей постоянного тока с использованием законов Ома, Кирхгофа, методом наложения.

Перед тем, как приступить к решению задач, студентам необходимо ответить на вопросы, содержащиеся в разделе «Подготовка к работе».

1. Дать определение электрическому току, указать условия существования электрического тока.

2. Дать определение линейной и нелинейной электрических цепей.

3. Дать определение ветви узла и контура электрической цепи. Указать, как могут быть соединены элементы, входящие в одну и ту же ветвь.

4. Указать признаки последовательного и параллельного соединения элементов.

5. Сформулировать законы Ома и Кирхгофа.

6.Записать формулы преобразования треугольника сопротивления в звезду.

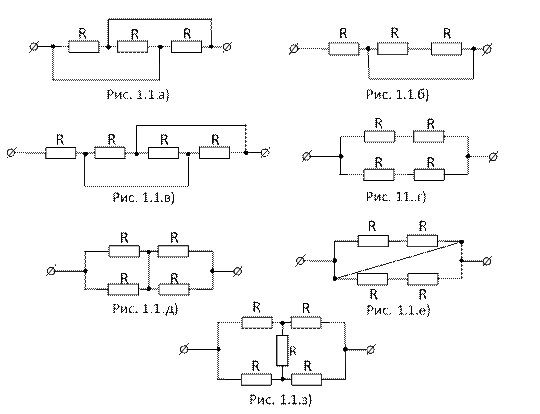
1.Определить эквивалентное сопротивление электрических цепей:

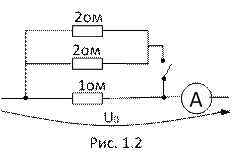
2.Как изменится показание амперметра после замыкания рубильника? U₀ – постоянное напряжение (рис.1.2).

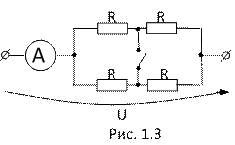
3.Как изменится показание амперметра, если замкнуть рубильник? U- постоянное напряжение.

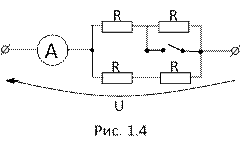
4.Что покажет амперметр после замыкания рубильника, если до замыкания он показывал 9А? U – постоянное напряжение (рис 1.4).

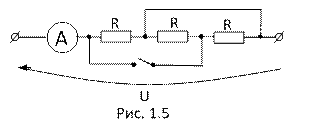
5. До замыкания рубильника амперметр показывал 6А (рис. 1.5). Что он покажет после замыкания рубильника, если U – постоянное напряжение?

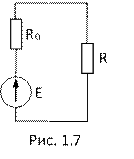
6. Для рис. 1.7 выразить напряжение U через параметры цепи (E, R₀, R).

7. Для цепи, изображенной на рис. 1.7, задано: E = 204В; R₀ = 1ом; R = 50 ом. Параллельно сопротивлению R подключается идеальный амперметр (R_A = 0). Что он покажет?

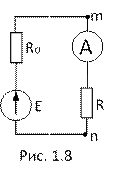
8. Для цепи, изображенной на рис. 1.8, задано: E = 204В; R₀ = 1ом; R = 50 ом. Что покажет амперметр (R_A = 0), если точки m и n замкнуть проводником с нулевым сопротивлением?

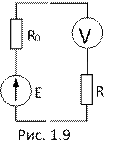
9. Что покажет вольтметр с бесконечно большим внутренним сопротивлением, включенный в цепь, как показано на рис. 1.9?

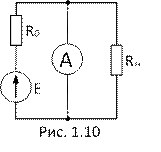
10. Чему будет равно показание амперметра с нулевым внутренним сопротивлением, включенного в цепь, как показано на рис. 1.10?

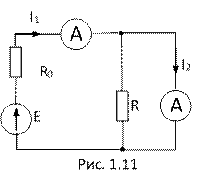
11. Два амперметра с нулевыми внутренними сопротивлениями включены в цепь, как изображено на схеме. Определить отношение их показаний.

12. Для цепи, изображенной на схеме, задано: E = 204В; R₀ = 1ом; R = 50 ом. В каком-либо месте разорвем цепь и включим в образовавшийся разрыв идеальный вольтметр (R_V = ∞). Что он покажет?

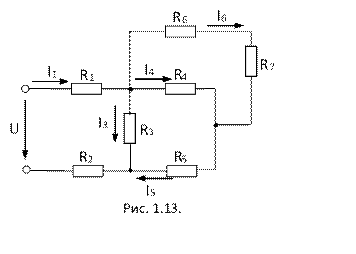
13.Найти распределение токов в схеме цепи, если R₁ = R₂ = 0,5ом; R₃ = R₄ = 6ом; R₅ = R₆ = 1ом; R₇ = 2ом, а напряжение на входе U = 120В. Определить мощность потребляемую цепью. Ответ: I₁ = 40А; I₃ = 13,33А; I₄ = 8,9А; I₅ = 26,7А; I₆ = 17,8А; P = 4,8кВт.

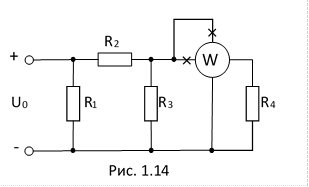
14.Для цепи, изображенной на схеме, задано: P = 75Вт; R₁ = 2ом; R₂ = 6ом; R₃ = 3ом; R₄ = 3ом. Расчитать токи во всех ветвях цепи и напряжения на резисторах, а также напряжение питания U.

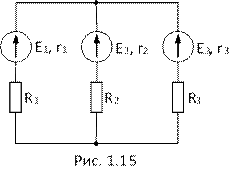
15.В цепи, изображенной на схеме, задано: E₁ = 10В; E₂ = 40В; E₃ = 5ом;

r₁ = 5ом; r₂ = r₃ =2ом; R₁ = 30ом; R₂ = 3ом; R₃ = 8ом. Определить токи в ветвях с помощью законов Кирхгофа. Составить уравнение баланса мощности.

1.2 Практическое занятие №2

Цель занятия – приобрести навыки расчета и анализа сложных цепей постоянного тока методом контурных токов, 2-х узлов, узловых потенциалов и эквивалентного генератора.

1. В чем состоит отличие сложной электрической цепи от простой.

2. Пояснить методику составления уравнений по методу контурных токов и правило знаков при составлении уравнений.

3. Пояснить методику составления уравнений по методу узловых потенциалов и как выбираются знаки слагаемых уравнений.

4. Для схемы с двумя узлами написать формулы:

— определения узлового напряжения и пояснить правило знаков для источников ЭДСЕ и тока I.

— определения токов в ветвях.

5. Пояснить, когда целесообразно применять метод эквивалентного

Источник

Раздел 1

Физические основы электротехники. Интегральные характеристики электромагнитного поля. Уравнения и законы электромагнитного поля в интегральной форме. Элементы электрических цепей и их модели.
Электрическая цепь. Положительные направления тока и напряжения. Мгновенная мощность и энергия.

Термины и определения основных понятий

Электротехника – наука, занимающаяся разработкой вопросов практического использования законов электромагнитных явлений.

Примечание — Напряженность электрического поля равна отношению силы, действующей на заряженную частицу, к се заряду и имеет направление силы, действующей на частицу с положительным зарядом

Примечание — Электрическое напряжение U12 вдоль рассматриваемого пути от точки 1 к точке 2 определяют по формуле:

,

где Е— напряженность электрического поля;

dl — бесконечно малый элемент пути;

r1 и r2 — радиусы-векторы точек 1 и 2.

Магнитное поле – одна из двух сторон электромагнитного поля, характеризующаяся воздействием на движущуюся электрически заряженную частицу с силой, пропорциональной заряду этой частицы и ее скорости.

Электромагнитное поле – вид материи, определяемый во всех точках двумя векторными величинами, которые характеризуют две его стороны, называемые «электрическое поле» и «магнитное поле», оказывающий силовое воздействие на электрически заряженные частицы, зависящее от их скорости и электрического заряда.

Идеальный элемент (электрической цепи) – абстрактное представление элемента электрической цепи, характеризуемое одним параметром.

Элемент (электрической цепи) – отдельное устройство, входящее в состав электрической цепи, выполняющее в ней определенную функцию.

Электрическая цепь – совокупность устройств и объектов, образующих путь для электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий об электродвижущей силе, электрическом токе и электрическом напряжении.

Участок (электрической) цепи – часть электрической цепи, содержащая выделенную совокупность ее элементов.

(электрическое) соединение – соединение участков электрической цепи, с помощью которого образуется электрическая цепь.

Параметр электрической цепи [элемента электрической цепи] – величина, характеризующая какое-либо свойство электрической цепи [элемента электрической цепи] в качественном и количественном отношениях.

Разнообразные электротехнические и электронные устройства представляют собой системы заряженных тел и контуров с токами, взаимодействующие друг с другом. Электромагнитные явления, происходящие в таких системах, определяются как процессами в заряженных телах и проводящих контурах с токами, так и физическими процессами в окружающих средах, в которых распространяется электромагнитное поле, характеризуемое векторами:

— электрической напряженности ,

— электрического смещения ,

— магнитной напряженности ,

— магнитной индукции .

Эти характеристики (,,, — являются дифференциальными т. к. характеризуют электромагнитное поле в каждой точке.

Процессы в электромагнитных полях описываются в макроскопическом понимании уравнениями Максвелла в интегральной форме, представляющими собой обобщение законов Ампера, Фарадея и Гаусса. Все эти законы изучены в курсе физики.

1. Закон полного тока (связь между, электрическим током и напряженностью магнитного поля).

— линейный интеграл напряженности магнитного поля по любому замкнутому контуру равен полному току сквозь поверхность, ограниченную этим контуром.

2. Закон электромагнитной индукции.

Устанавливает связь между электрическим полем и возбуждающим его переменным магнитным полем.

Уравнение является обобщением закона электромагнитной индукции Фарадея: ЭДС, возникающая в контуре при изменении магнитного потока сквозь поверхность, ограниченную данным контуром равна взятом со знаком минус скорости изменения магнитного потока,

а т. к. то (2)

3. Это обобщение закона Гаусса устанавливает связь электрического поля, окружающего заряженные частицы и тела с величиной электрического заряда.

(3)

Поток вектора электрического смещения сквозь любую замкнутую поверхность в любой среде равен свободному заряду, заключенному в объеме, ограниченном этой поверхностью.

4. Устанавливает соленоидальность магнитного поля. Линии вектора магнитной индукции всюду непрерывны Поток вектора магнитной индукции через любую замкнутую поверхность .

Поговорим и некоторых физических величинах, входящих в уравнения (1-4).

; — закон Кулона; .

— ток проводимости – представляет собой упорядоченное движение электронов в металле или ионов в электролите: .

— ток переноса – возникает под действием электрического поля в свободном пространстве, заполненном зарядами со среднеобъемной плотностью , движущимися со скоростью .

, где — плотность тока переноса.

— ток электрического смещения – возникает в диэлектриках и связан с переменным электрическим полем.

, где — плотность тока смещения.

Токи проводимости и переноса могут возникать как в постоянных, так и в переменных электрических полях. Ток смещения присутствует только в переменных полях. Это значит, что в переменных полях линии вектора плотности тока проводимости могут иметь продолжением линии вектора плотности тока смещения.

В общем случае расчет электромагнитных систем сводится к решению уравнений Максвелла для электромагнитного поля. Решение этих уравнений даже для сравнительно простых электромагнитных систем крайне сложно. Поэтому во многих практических случаях, когда в системе можно выделить отдельные элементы, связанные только с одним видом поля (электрическим или магнитным), можно отказаться от исследования электромагнитного поля и решать задачу, рассматривая систему как электрическую цепь, которая в отличие от электромагнитной системы описывается не векторами ,,,, а интегральными величинами:

— электрическим напряжением

— электрическим током

— Э. Д.С.

— магнитным потоком .

т. к ; ; ;

и перейти от теории электромагнитного поля к теории электрических и магнитных цепей.

Условное графическое изображение электрической цепи называется электрической схемой. Она показывает, как осуществить соединение эле­ментов цепи (рис.1.1).

Ветвь (электрической цепи) – участок электрической цепи, вдоль которого протекает один и тот же ток.

Узел (электрической цепи) – место соединения ветвей электрической цепи.

Любой замкнутый путь, проходящий по нескольким ветвям, называ­ется контуром.

Контуры называются независимыми, если каждый из них содержит хотя бы одну ветвь не вошедшую во все остальные.

Численно ток определяется как предел отношения количества электри­чества, проходящего через поперечное сечение проводника за интервал вре­мени , при стремящимся к нулю: .

Маленькие буквы обозначают мгновенные значения величин ().

Если через поперечное сечение проводника за одинаковые промежутки времени переносится одинаковое количество заряда (и по знаку) то ток назы­вается постоянным.

.

Электрическая цепь в общем случае состоит из источников и приёмни­ков электрической энергии и проводов.

В источниках энергии (аккумулятор, электромагнитные генераторы) хи­мическая, механическая, тепловая энергии превращаются в электрическую, а в приемниках (двигатели, резисторы и т. д.) происходит обратное преобразо­вание энергии.

При расчёте режимов работы электрических цепей пользуются идеали­зированными моделями электротехнических устройств, называемыми эле­ментами цепи.

Сопротивлением называют идеализированный элемент цепи, прибли­женно заменяющий резистор (рис. 1.2), в котором происходит преобразование электрической энергии в тепловую.

Сопротивление идеального резистора постоянно, и не зависит ни от ка­ких факторов. Сопротивление реального проводника увеличивается с ростом частоты переменного тока (поверхностный эффект).

Термин «сопротивление» и соответствующее обозначение применяется как для обозначения самого элемента цепи, так и меры противодействия про­водящей среды перемещению носителей электрических зарядов.

— в цепи постоянного тока, — проводимость

.

Это идеализированный элемент цепи, приближающийся по свойствам к индуктивной катушке, в котором накапливается энергия электромагнитного поля (рис.1.3).

Идеальная индуктивность имеет нулевое сопротивление для постоянного тока. Реальная катушка имеет конечное, не равное нулю сопротивление.

Термин «индуктивность» и « L » применяются как для обозначения са­мого элемента цепи, так и для количественной оценки отношения потокосце­пления самоиндукции к току в данном элементе.

, .

Потокосцепление это сумма произведений магнитных потоков на числа витков, с которыми они связаны.

, .

Это идеализированный элемент цепи, приближённо заменяющий кон­денсатор, в котором накапливается энергия электрического поля (рис. 1.4).

В идеальной ёмкости отсутствуют тепловые потери. В диэлектрике ре­ального конденсатора, при переменном токе, вследствие поляризации возни­кают тепловые потери, которые возрастают с увеличением частоты.

В действительности они всегда сопутствуют друг другу.

Электрические цепи, состоящие только из линейных элементов, называ­ются линейными. В них выполняется принцип суперпозиции (наложения).

Положительные (условно) направления тока и напряжения.

Для расчета электрических цепей необходимо учитывать направления токов и напряжений. Направление тока характеризуется знаком тока. Понятие положительный и отрицательный ток имеет смысл, если только сравнивать направление тока с некоторым заранее выбранным ориентиром – так назы­ваемым положительным направлением. Его выбирают произвольно и указы­вают стрелкой.

Если в результате расчета тока, выполненного с учётом выбранного по­ложительного направления тока получился положительный, то это значит, что его фактическое направление совпадает с выбранным, если отрицатель­ный – противоположно выбранному.

Мгновенная мощность и энергия

Двухполюсником называется электрическая цепь, содержащая два за­жима (рис.1.6).

Активный двухполюсник содержит источники энергии, пассивный – нет.

Пусть через участок ab под воздействием приложенного напряжения U проходит заряд dq . Поступающая при этом в приемник элементарная энергия равна:

.

— энергия, поступающая в приёмник за время

в цепи постоянного тока:

Если образующие цепь проводники неподвижны (т. е. не совершается механической работы), а ток постоянен, то работа сторонних сил источ­ника энергии целиком расходуется на нагрев. Количество теплоты, выде­лившееся при прохождении постоянного тока в проводнике с сопротивле­нием r равно:

Производная энергии по времени (скорость поступления энергии в цепь в данный момент времени) представляет собой мгновенную мощ­ность.

Мгновенная мощность – величина алгебраическая, её значение поло­жительно при одинаковых знаках напряжения и тока на зажимах активного двухполюсника (говорят, источник отдает энергию в цепь), и отрицательна при разных знаках (энергия возвращается из рассматриваемого участка цепи в источник).

Частный случай: , если .

Рассеиваемая в резисторе мощность всегда положительна, так как протекание тока в нем сопровождается необратимым процессом нагрева­ния проводника.

В любой электрической цепи, по закону сохранения энергии, количе­ство вырабатываемой в единицу времени энергии источников должно быть равно потребляемой, то есть электрическая мощность источников должна быть равна мощности потребителей.

Если направление источника ЭДС и тока, протекающего через него, совпадают, то источник отдаёт энергию и произве­дение входит в ле­вую часть равенства со знаком плюс. В противном случае источник потреб­ляет энергию и берётся со знаком минус.

Если схема содержит источник тока то в общем случае его мощность записывается как , где — падение напряжения на зажи­мах. Направление передачи энергии зависит от знака напряжения на за­жимах источника.

Например, для схемы изображенной на рис.1.7: ;.

1. Сформулируйте закон полного тока, теорему Гаусса. и закон электромагнитной индукции.

2. В чем заключается принцип непрерывности магнитного потока?

3. При каком условии при решении задачи можно перейти от теории электромагнитного поля к теории электрических цепей?

4. Что называется электрической схемой, ветвью, узлом, контуром, незавиимым контуром?

5. Из чего состоит электрическая цепь?

6. Сформулируйте понятие «элемент электрической цепи»?

9. Дайте определение понятий «мгновенная мощность» и «энергия»

10. В чем заключается баланс мощностей?

Упражнения и задачи

Ответ: выходящих линий больше.

2. Определить напряженность электрического поля меж­ду двумя

равномерно заряженными параллельными пласти­нами с

поверхностной плотностью заряда а (краевым искаже­нием поля

пренебречь). Диэлектрическая проницаемость среды ε.

3. До замыкания рубильника (см. схему) амперметр по­казывал 6 А. Что он покажет после замыкания рубильника, если U — приложенное

4. Временная диаграмма на зажимах активного сопротивления Ом изображена на рис 1.

Определить значение тока в момент времени

5. Используя данные примера 4, записать уравнение мгновенной мощности в промежутках 0 – 0,5 с и 0,5 – 1 с; построить временную диаграмму мощности.

Источник