Для чего служит масштаб в черчении
Чертежик
Метки
Масштабы чертежей
Масштабы чертежей. Масштабом называется отношение линейных размеров изображения предмета на чертеже к действительным размерам предмета.
Масштабы чертежей бывают численные, линейные, поперечные (десятичные) и угловые (пропорциональные).
Численный масштаб обозначается дробью, которая показываем кратность увеличения или уменьшения размеров изображения на чертеже. Численный масштаб обозначается дробью, которая показываем кратность увеличения или уменьшения размеров изображения на чертеже.
В зависимости от сложности и величины изображения, ею назначения, стадии проектирования на чертежах применяются:
1.) Масштабы уменьшения: 1:2; 1 :2,5; 1:4; 1 : 5; 1 : 10; 1 : 15; 1:20; 1:25; 1 : 40; 1:50; 1:75; 1: 100; 1:200; 1:400; 1:500; 1:800; 1:1000. (
Пример: допустим дана длина 5000 мм. Необходимо начертить в масштабе 1:100, то чертится отрезок размером 50 мм.)
При проектировании генеральных планов крупных объектов допускается применять масштабы: 1:2000; 1:5000; 1: 10000; 1:20000; 1:25000; 1: 50000.
2.) Масштабы увеличения: 2:1; 2,5:1; 4:1; 5:1; 10:1; 20:1; 40:1; 50:1; 100: 1.
Пример: допустим дана длина 50 мм. Необходимо начертить в масштабе 2:1, то чертится отрезок длиной 100 мм.)
В необходимых случаях допускается применять масштабы увеличения 100-n : I. где n — целое число.
3.) Натуральная величина: 1:1.(пример: длина детали 10 мм., соответственно, чертим линию размером 10мм. )
Масштаб должен указываться на всех чертежах, кроме некоторых строительных, а также чертежей, воспроизводимых путем клиширования или фотографирования.
Если на листе все чертежи выполнены в одном масштабе, то его значение проставляют в соответствующей графе основной надписи по типу 1:1; 1:2; 2:1 и т. д. Если на одном листе помещены чертежи разного масштаба, то масштаб указывают под названием соответствующего чертежа но типу М1:1; М1:2 и т. д.
Угловые (пропорциональные) маштабы применяют для построения изображений в уменьшенном или увеличенном в несколько раз виде.
Угловым масштабом целесообразно пользоваться, когда масштаб чертежа неопределенный 1 : n, где n может быть любое целое или дробное число и при ограниченном количестве размеров на чертеже.
Применение масштабов смотрите в примерах чертежей и в разделе чтение сборочного чертежа
Что такое масштаб, для чего нужен и что он показывает
Чтобы изобразить предметы, которые имеют размер больше листа, на котором планируется его рисовать, используется такое понятие, как масштаб. Что такое масштаб? Что обозначает данное понятие и как оно применяется на практике?
Что такое масштаб
С немецкого языка, слово «masstab» дословно переводится, как «мерная палка». Что показывает масштаб? Эта величина показывает, какое соотношение величины оригинального предмета и его изображения. Его принято использовать в математике, географии, картографии, моделировании, программировании, проектировании и других науках. Проще говоря, масштаб – соотношение реального и изображенного размеров.
Какие бывают масштабы
Масштаб, указанный на чертеже или карте, может быть изображен числом или графически. Поэтому выделяют несколько разных видов масштаба:
Как использовать масштаб
Для чего нужен масштаб и что он показывает, уже узнали. Но, как ним правильно пользоваться? К примеру, на карте есть два населенных пункта А и Б, а вам необходимо узнать, какое между ними расстояние. Согласно карте, ее масштаб составляет 1:50 000. Чтобы определить расстояние между населенными пунктами, измеряем при помощи обыкновенной линейки расстояние, которое есть между ними на карте. У нас получилось 5 см. Теперь, нам осталось 5 умножить на 0,5 (так как согласно масштаба в 1 см карты – 0,5 км в реальности). Проведя простые расчеты, мы получили, что расстояние между населенными пунктами А и Б равно 2,5 км.
Разновидности карт
Именно масштаб является одним из основных критериев, по которому принято классифицировать географические карты. Исходя из этого, все карты делят на:
Местность, показанная на крупномасштабной графической карте, будет более детализована и чем крупнее масштаб нанесен на карте, тем соответственно больше различных объектов мы сможем на ней показать.
Мелкомасштабные географические карты применяются для передачи данных о континентах или полушариях. Среднемасштабные подходят для изображения стран. А на крупномасштабных, принято показывать небольшие по размеру объекты. Обычно их используют туристы, военные и т.д.
Масштаб в черчении
С данным понятием школьная программа знакомит не только на уроках географии, но и в черчении. Здесь он используется для детального изображения различных предметов. От географического масштаба, чертежный отличается тем, что здесь, наоборот, он применяется для увеличения на рисунке мелких деталей или их частей. К примеру, чтобы показать винтик и т.д.
В данном случае, масштабирование нам помогает детальнее рассмотреть мелкий предмет. Записывается масштаб на чертеже, тоже в перевернутом виде 100:1. Это значит, что 100 метрических единиц предмета, который изображен на данном чертеже, соответствуют 1 единице его размера в действительности.
Материал по технологии «Масштабы»
Описание разработки
Для изображения на чертежах очень крупных или слишком мелких изделий (самолеты, часы) используют масштабы.
Масштаб — это отношение размеров изображения действительным размерам предмета.
Если изображения на чертежах имеют такие же размеры, как и действительные размеры детали, считается, что чертежи выполнены в натуральную величину, или в масштабе 1:1 (один к одному). Если изображения на чертеже имеют размеры больше действительных размеров детали, то для их построения использован масштаб увеличения. Если изображения на чертеже имеют размеры меньше действительных размеров детали, то для их построения использован масштаб уменьшения.
— масштаб натуральной величины — 1:1.
— масштабы уменьшения — 1:2; 1:2, 5; 1:4; 1:5; 1:10; 1:15; 1:20; 1:25; 1:40; 1:50; 1:75; 1:100; 1:200; 1:400; 1:500; 1:800; 1:1000.
— масштабы увеличения — 2:1; 2, 5:1; 4:1; 5:1; 10:1; 20:1; 40:1; 50:1; 100:1.
При любом масштабе на чертеже всегда наносят только действительные размеры. Масштаб записывают в специальной графе основной надписи по типу 1:1; 1:2; 2:1 и т. д. Масштаб может быть проставлен на поле чертежа только для тех изображений, которые выполнены в масштабе, отличном от масштаба, заявленного в основной надписи. В этом случае над изображением делают запись М 1:2; М 2:1 и т. д.
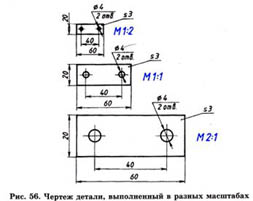
Сопоставьте изображения, выполненные в различных масштабах (рис. 56).
Чтобы построить чертеж детали в масштабе 2:1, необходимо линейные размеры изображения увеличить в два раза. Если необходимо выполнить изображение в масштабе 1:2, то линейные размеры уменьшаются в два раза. Размеры углов не изменяются при выборе масштаба изображения.
Вопросы и задания
1. Что такое масштаб?
2. Какие масштабы установлены стандартом?
3. Для чего необходимы масштабы?
4. Где указывается масштаб изображения на чертеже?
5. Где и как указывается масштаб изображения, если он отличается от указанного в основной надписи?
6. В рабочей тетради на листе бумаги в клеточку выполните чертеж картонной прокладки (рис. 57) в масштабе 2:1.
Урок черчения «Правила оформления конструкторских документов-чертежей: масштабы; нанесение размеров на чертеже»
Разделы: Технология
Цель урока: Формировать у учащихся знание правил ГОСТ ЕСКД по оформлению конструкторских документов-чертежей. Сформировать представление о масштабах и их обозначениях. Обеспечить в ходе урока знакомство с правилами нанесения размеров на чертежи и другие технические документы.
Образовательная. Закрепить усвоение понятий ГОСТ ЕСКД. Сформировать знания понятия масштаб и правил нанесения размеров на чертежи.
Развивающая. Развитие пространственных представлений, наблюдательности, логического мышления, самостоятельного анализа, умений применять формируемые знания в новых ситуациях.
Воспитательная. Формировать у учащихся представление о роли чертежа, как интернационального языка техники.
Вид урока: стандартный классический.
Для реализации цели и задач урока использовались различные методы и приемы обучения, т.е. способы современной деятельности учителя и учащихся, направленные на решение дидактических задач обучения.
1) Применяемые методы из классификации по источнику получения знаний.
Словесные методы.
Объяснение – монологическая форма объяснения, словесное истолкование
Беседа – диалогический метод обучения
Эвристическая беседа – подведение учащихся к пониманию новых знаний, создание проблемной ситуации.
Метод демонстраций – демонстрация приемов нанесения размеров на чертеж, наглядных пособий.
Практическая деятельность учащихся – выполнение задания по определению правильности нанесения размеров на чертеж
2) Средства обучения.
Материальные – кабинет, мебель, микроклимат, доска, мел, наглядные пособия, карточки для индивидуальной работы, чертежные принадлежности, рабочая тетрадь.
Идеальные (умственные действия).
Вербальные – речь (обмен информацией между участниками учебного процесса).
Материализованные – схемы нанесения размеров на чертеж, выполненные учителем во время объяснения нового материала.
3) Форма организации работы учащихся.
Фронтальная – учитель ведет работу со всем классом одновременно (объяснение, показ); все ученики выполняют одинаковую, общую для всех работу (обсуждение).
Индивидуальная – каждый ученик самостоятельно выполняет задание, предложенное учителем.
1. Организационный момент.
Цель: Поздороваться с детьми, настроить их на работу.
2. Проверка предыдущих знаний
Цель: Подготовить переход к новой теме.
Прежде чем мы начнём проходить новую тему, следует повторить некоторые понятия предыдущего урока.
Вопрос 1: Что такое ГОСТ?
Ответ: Государственный стандарт – документ, устанавливающий комплекс норм, правил, требований.
Вопрос 2: Что такое ЕСКД?
Ответ: Единая система конструкторских документов – комплекс стандартов, устанавливающих правила и положения по порядку разработки и оформлению конструкторских документов
Вопрос 3: Что такое формат?
Ответ: Лист определённого размера.
Вопрос 4: Какие форматы вам известны?
3. Введение в тему урока.
Цель: Создать эмоциональный настрой на восприятие темы урока.
4. Объяснение учителем новой темы
Цель: Сформировать представление о масштабах и их обозначениях. Обеспечить в ходе урока знакомство с правилами нанесения размеров на чертежи и другие технические документы.
В практике приходится выполнять чертежи различных изделий. Не всегда размеры изделия и размеры форматов бумаги позволяют выполнить чертеж в натуральную величину. В таких случаях чертеж выполняют в измененном виде, т.е. в некотором масштабе.
Масштаб – это отношение линейных размеров изображаемого предмета на чертеже к его натуральным действительным размерам.
ГОСТ устанавливает следующие масштабы.
Масштабы уменьшения: 1:2; 1:2,5; 1:4; 1:5; 1:10; 1:15; 1:20; 1:25; 1:40; 1:50; 1:75; 1:100;…
Натуральный масштаб: 1:1
Масштабы увеличения: 2:1; 2,5:1; 4:1; 5:1; 10:1; 20:1; …
Для определения величины изображенного изделия или какой- либо его части по чертежу на нем наносят размеры.
6. Практическая работа с классом.
Цель: Закрепление полученных знаний, путем совместного анализа чертежа детали, осмысление материала учениками
Определить ошибки на чертеже детали предложенном учителем. (Рисунок 11)
О1 — ненужно указывать миллиметры при обозначении линейных размеров
О2 — размерные числа на параллельных размерных линиях должны стоять в шахматном порядке
О3 — размерные линии должны заканчиваться стрелкой
О4 – размерные числа ставят слева от вертикальной размерной линии
О5 – при обозначении диаметра необходимы две размерные стрелки
О6 – так как в детали два одинаковых отверстия необходимо это указать при помощи надписи “2 отв.”
О7 – размерную линию проводят из центра дуги, размерная стрелка упирается в точку окружности.
О8 — на чертеже изображена дуга, поэтому необходимо указать размер радиуса (прописную латинскую букву R).
О9 – цент окружности должен лежать на пересечении штрихов штрихпунктирной линии
О10 – перед размерным числом должна стоять буква S, которая обозначает толщину детали.
7. Индивидуальная практическая работа.
Цель: Закрепление полученных знаний, путем самостоятельного анализа и логического мышления
Напишите номер чертежа, на котором правильно проставлены размеры детали.
Ответы: правильными являются варианты 1 – для всех нечетных заданий, варианты 2 – для всех четных заданий.
8. Подведение итогов.
Цель: Формирование эмоционально-оценочного отношения к чертежу
Цель: Применение полученных знания в новых ситуациях, подготовка к графической работе.
Ботвинников А.Д., Виноградов В.Н., Вышепольский И.С. Черчение, учебник для 7-8 классов средней школы. Параграф № 2.5; 2.6; рис.36а стр.30 (задание к графической работе № 2), выполнять в тетради.
10. Организационный момент.
Цель: Поблагодарить учеников за урок, попрощаться с детьми.
Онлайн конвертер длины, перевод всех систем измерения, метрическая, британо-американская, старорусская, морская, астрономическая, типографская
Какими бывают масштабы чертежей?
ГОСТ различает три вида масштабов: натуральной величины, уменьшения и увеличения.
Когда 1 сантиметр на бумаге равен 1 сантиметру величины объекта, то чертеж имеет масштаб натуральной величины. Он носит численное обозначение 1:1 и используется в машино- и приборостроении.
Масштаб уменьшения применяют, когда размер изображаемого элемента больше бумаги, на котором его можно начертить.
Чтобы не брать несколько листов, объект пропорционально уменьшают на изображении. Масштаб записывается как отношение чисел, где в числителе обязательно стоит единица. Это значит, что объект на чертеже в кратное количество раз уменьшен относительно натурального размера. Например, отношение на чертеже 1:1000 означает, что 1 см изображения соответствует 10м. Помните, что масштаб 1:3 не используется как масштаб уменьшения, т.к. получаются дробные значения при делении на 3. Сейчас,когда расчеты проводятся на компьютере, это не является проблемой. Тем не менее, в ГОСТ размера 1:3 нет.
Номенклатура применяемых значений строго регламентирована ГОСТ. Для масштабов уменьшения допускаются следующие пропорции:
Масштаб уменьшения применяют в промышленном и гражданском строительстве. Для этой отрасли существует отдельный набор нормативных документов по оформлению чертежей. Масштабы для изображения строительных планов, фасадов, разрезов и узлов, регламентируются ГОСТ 21.501-2011, Таблица 1:
Отдельно для градостроительства ГОСТ допускает использование масштабов 1:2000; 1:5000; 1:10000; 1:20000; 1:25000; 1:50000. Это нужно для нанесения на генеральный план территорий с большой площадью.
Масштаб увеличения используется, когда размер какой-нибудь детали мал и для удобства его изображение нужно увеличить.
Такой тип масштаба удобнее для чтения, чем 1:1. Обозначают масштаб увеличения отношением, где единица находится в знаменателе. Соответственно, в 10 сантиметрах чертежа передан 1 сантиметр реальной детали.
Нормативом предложены следующие масштабы:
Масштаб увеличения применяют реже, допустимые соотношения находятся в диапазоне 1001:1 до 1009:1. Используется, как масштаб натуральной величины, преимущественно в машиностроении и приборостроении.
Что такое длина и как ее измерить
Длина — это физическая мера расстояния между двумя точками в пространстве. Она измеряется в соответствии с евклидовой метрикой (классический метод измерения расстояний) и, как правило, обозначается буквой L. Она может быть измерена по прямой линии (например, длина волны, расстояние между полом и потолком), по кривой (например, длина пути, пройденного объектом).
Базовая единица измерения длины (согласно системе СИ) — это метр. Точное определение метра было принято на 17-ой Генеральной конференции мер и весов в 1983 году. 1 м — это расстояние, которое свет проходит в вакууме за время 1/299 792 458 с.
Длина никогда не может принимать отрицательные значения.
Для измерения длины используются такие устройства, как:
Для преобразования в разные системы используют конвертер длины
Как правильно обозначать масштаб на чертеже?
При оформлении чертежей следуйте установленным правилам и нормам. Масштаб указывается в числах, записывается дробью в отведенной для него графе штампа.
Иногда возникают ситуации, когда на одном листе необходимо разместить изображения разных масштабов. Например, план кровли 1:200 и узел сопряжения ее элементов 1:25. Тогда масштаб плана 1:200 указываем в штампе, а масштаб узла 1:25 вместе с его номером непосредственно над изображением сопряжения.
Меры длины. Несколько фактов из истории
Самыми древними единицами измерения длины, которые люди использовали чаще всего, были части тела (локоть, палец, ступня, шаг и т.д.).
В Древнем Египте это были локти, руки или пальцы.
Древние римляне измеряли расстояния ступнями (foot- фут). Более короткие участки меряли шириной большого пальца. Для определения длины больших размеров использовали шаги.
Тысяча шагов римского солдата была милей
Торговцы текстилем установили единицу измерения, известную как ярд — это длина от подбородка до кончиков пальцев вытянутой руки. Придерживая материал подбородком, они вытягивали руку, таким образом измеряя длину отреза.
Еще есть версия что ярд ввел в обиход король Англии Эдгар и он равнялся расстоянию от кончика его носа до среднего пальца вытянутой руки. Поскольку короли менялись и их телосложение соответственно тоже, то это вносило немалую путаницу в системе измерений.
Размер и Масштаб
Остроумный государственный деятель сказал: «Используя числа, вы можете доказать всё, что угодно».
Модели кораблей бывают разных размеров, от микроскопических до огромных. Вам, возможно, понадобится увеличительное стекло, чтобы увидеть некоторые из них; На другие вы можете подняться на борт. Точные копии Golden Hind и Mayflower II — тоже модели. Фактор, определяющий размер модели корабля — масштаб. В каком масштабе строить и как его выбирать – это является предметом рассмотрения этой части. Масштаб — отношение одного размера к другому, выраженное в сравнительных единицах. Размеры должны принадлежать одной системе измерения. Вы не можете оперировать одновременно и футами и метрами. Сначала вы должны преобразовать один размер в другой. Для примера остановимся на самом популярном масштабе, используемом железнодорожными моделистами. Итак, масштаб 1/4 дюйма = 1 фут. Что это означает? Это означает, что 1 дюйм будет равняться 4 футам. Каждый фут моделируемого предмета должен быть представлен на рисунке как 1/4 дюйма. Как мы получили это число? Если мы делим 1 дюйм на четверти, то получаем 48 единиц в 1 футе (12 дюймов x 4 части = 48). Если выразить это как масштаб, мы можем сказать, что 1 единица равна 48 единицам. Мы могли бы просто сказать, что это — 1:48. Если хотите, можете написать это дробью: 1/48. Это означает то же самое. В десятичном эквиваленте это становится 0,25. Спросите железнодорожного моделиста и он скажет без колебания, что это – типоразмер 0. Наша модель корабля, основываясь на пропорции 1/4 дюйма к футу, будет как 1/48 реального корабля. Это — модель «масштаба одной четвертой» (quarter-scale). «Масштаб одной четвертой» — это термин, не путайте его с размером. Модель — не 1/4 размера оригинала, а 1/48 его размера. Надеюсь, это было не очень трудно. Хотите пробовать еще? На этот раз давайте использовать масштаб одной восьмой. Разделив 1 дюйм на 8 частей и умножив на 12 дюймов, вы получите 96 единиц в 1 футе. Это дает нам отношение 1:96. Теперь разделите 12 на 96, и у нас получится десятичный эквивалент 0,125. Это – «масштаб одной восьмой». Наш друг, железнодорожный моделист назвал бы это типоразмером HO. Вы не должны быть умственным гигантом, чтобы уметь вычислять масштаб. Все, что вам надо — острый карандаш, немного бумаги, образование начальной школы и, если необходимо, современная математическая соска — калькулятор. Становится просто нелепо, если вы не можете понять несколько основных идей (ТАБЛИЦА 5-1).
Сравнение масштабов и эквивалентов
| Дробный дюйм | Десятичный эквивалент | Масштаб | Отношение дюйма к футу |
| 1/16 | 0,0625 | 1/192 | 1″ = 16′ |
| 3/32 | 0,0936 | 1/128 | 1″ = 10,5 |
| 1/8 | 0,1250 | 1/96 | 1″ = 8′ |
| 11/64 | 0,1666 | 1/72 | 1″ = 6′ |
| 3/16 | 0,1875 | 1/64 | 1″ = 5,2′ |
| 1/4 | 0,250 | 1/48 | 1″ = 4,0′ |
| 19/64 | 0,300 | 1/40 | 1″ = 3,3′ |
| 11/32 | 0,343 | 1/35 | 1″ = 3,9′ |
| 3/8 | 0,375 | 1/32 | 1″ = 2,6′ |
| 1/2 | 0,500 | 1/24 | 1″ = 2,0′ |
Очевидно, что масштаб означает отношение одного размера к другому. Для иллюстрации, давайте рассматривать объект, который мы можем легко представить: 6-футовый человек. С помощью математики, мы собираемся уменьшать его в размере, используя масштаб. Представьте нашего джентльмена в масштабе 1:32. Мы теперь имеем точную копию наших шести футов длиной только в 2 1/4 дюймах. Уменьшите до масштаба 1:35, и он стал 2-дюймовой моделью. В масштабе 1:40, он равен 1 3/4 дюйма. Используя популярный масштаб одной четвертой (quarter-scale), или 1:48, он уменьшился до 1 1/2 дюйма; 0.996 дюймов в масштабе 1:72. Обратите внимание, чем число в основании дроби становится больше, тем не менее наш объект становится меньше. Поскольку мы приближаемся к масштабу 1:200, давайте остановимся, прежде чем потеряем его в пыли на рабочем месте (Рис. 5-1).
Рис. 5-1. Сравнение масштабов и размеров
Что означают все эти дроби? Давайте попробуем разобраться. Популярный масштаб, 1/4 дюйм = 1 фут. Мы установили, что 1 дюйм, равный четырем футам размера оригинального объекта, выражен в единицах. Единица измерения — та же самая единица, в частях которой мы имеем размеры оригинала. Давайте заменим дюймы и футы метрами. Большинство наборов, которые изготовлены в других странах, сделаны в метрическом масштабе. Число в числителе нашей дроби обозначает одну полную единицу измерения. Число в знаменателе — количество единиц, которые заменяет в масштабе одна полноразмерная единица измерения. В этом случае единица измерения — 1 метр. Слова предупреждения: размеры в метрической системе обозначаются в десятых частях метра. Так, например, миллиметр означает 1/1000 метра. Один сантиметр, от латинской сотни, означает 1/100 метра. Наиболее популярные — 1:50, 1:70, и 1:98 масштабы. Цифра в основании дроби показывает, сколько частей единицы требуется, чтобы представить одну единицу этой специфической системы исчисления. Если вам неудобны метрические размеры, вы можете их легко преобразовать в дюймы. Для этого умножьте миллиметры на 0.039370. Чтобы преобразовывать дюймы в миллиметры, умножите дюймы на 25.4. Чтобы преобразовывать сантиметры, переместите десятичную точку на одну позицию влево (0.39370 и 2.54). Для лучшего понимания того, как выбор масштаба может повлиять на конечный результат, давайте сравнивать два корабля в одном масштабе. Первый — эсминец реальной длиной 376 футов (115 метров). Другой — шхуна длиной 136 футов (41 метр). Масштаб 1:48, (1/4 дюйма к футу или «масштаб одной четвертой»). Модель эсминца будет 76 1/2 дюймов (195 см) в длину, в то время как модель шхуны будет 34 дюйма (86 см). Если вы всё же будете делать их в этом масштабе, вы должны сначала подумать, где вы собираетесь показывать или хранить эсминец. Далее несколько примеров использования масштаба, определение размера, и т.д., который мог бы повлиять на ваш выбор масштаба для постройки модели судна. Мой друг, который теперь проживает в Европе, прислал мне набор для изготовления рыбацкой лодки, которая является весьма популярной в его регионе. Масштаб не был обозначен ни на чертежах, ни на коробке. Небольшое исследование о лодках этого региона быстро установило, что они были обычно 36-38 футов длиной. Размеры чертежей показали, что модель будет 12 1/2 дюйма длиной и 3,875 дюймов шириной. Так как, согласно тексту, размеры лодок несколько различались, я выбрал оптимальный размер: 36 фута и 3 дюйма в длину и 10 футов и 10 дюймов в ширину. Длина была преобразована в дробь 36,25. Длина модели была разделена на длину реальной лодки: 12,5/36.25 = 0.0344. Если мы разделим 12 (в футе 12 дюймов) на 0.0344, мы получаем отношение 1:35. Это, как вы видите, очень близко к известному масштабу. Я полагаю, что вы не возражаете против небольшой разницы. Так как 1:34 — близко к 1:35, я буду использовать табличный масштаб. Фактические вычисления указывают, что законченная модель будет 12,4999 дюймов. Это достаточно приемлемо для меня. Важным понятием является десятичный эквивалент. Чтобы находить десятичный эквивалент, разделите масштаб на 12. Для 1:32, 12:32 = 0.375. Для 1:40, 12 разделить на 40 равняется 0.300. Для преобразования размера модели в размер оригинала, умножьте размер модели на единицы масштаба. Например, (модель длиной 34 дюйма, масштаб 1:48) 34 дюйма умножаем на 48, получаем 1632 дюйма. Чтобы преобразовать в футы разделите на 12. Ответ – 136 футов. Есть несколько способов определения размеров. Если у вас под рукой чертеж, выполненный в масштабе, то самый простой путь: прямое измерение на чертеже циркулем или другим измеряющим устройством. Есть также несколько способов изменить масштаб, если вы имеете все факты в наличии и все чертежи под рукой. Используя масштаб, берут размер на чертеже. Переводят размер в нужный масштаб. Изменяя «масштаб одной четвертой» до «масштаба одной восьмой», возьмите размер в «масштабе одной четвертой», и преобразуйте размер в «масштаб одной восьмой». Удвоив масштаб, вы проделали бы ту же процедуру. Это справедливо и для метрических масштабов. Вы также можете использовать пропорциональный циркуль, чтобы изменить масштаб. Пропорциональный циркуль — пара ног равной длины, в которых просверлили отверстия на расстояниях, показанных на Рис. 5-2. Убедитесь, что отверстия просверлены точно. На концах вставлены гвоздики или иглы для более точного измерения. Вы можете использовать сложные математические вычисления, и извести кучу бумаги. Я предпочитаю эмпирический метод для изменения масштаба. Этот метод изменять масштаб, который я назвал щелчком (flip-flopping), является весьма удобным для “lifting and lofting”, будет объясняться в Части 7.
Рис. 5-2. Как сделать пропорциональный циркуль.
Другие единицы длины
Помимо вышеперечисленных, существуют другие единицы для измерения длины. Их использование зависит от вида и места замеров.
Ангстрем (Å) — предназначен для численного выражения очень малых значений длины, сравнимых с размером атомов. Он равняется 10−10 м или одна десятимиллионная миллиметра. Ангстрем назван в честь Андерса Йонаса Ангстрема, шведского физика и астронома, одного из основоположников астрофизики и пионера спектроскопии. Впервые его представили в 1868 году. Ангстрем часто используется в химии и физике для описания объектов и явлений, происходящих в атомном масштабе. Например, атом водорода имеет радиус 0,37 Å, а длина связи H — H в молекулах H2 немного больше 1 Å. В ангстермах измеряют длину волн излучения, например, видимого, ультрафиолетового, рентгеновского и т.д. Микрометр (мкм или µm) — кратный метру (одна миллионная часть), является единицей длины в системе СИ. 1 мкм = 10−6 м, 1000 мкм равняется 1 мм.
В прошлом эта единица называлась микрон от греческого слова μικρός (мелочь). Название микрона и символ были официальными в 1879-1967 годах.
Морские
Кабельтов — единица расстояния, используемая в навигации. 1 кабельтов = 0,1 морской мили = 608 футов = 185,2 метра.
Морская миля — это единица расстояния, используемая в морской навигации и авиации. Это длина дуги земного меридиана, соответствующая одной угловой минуте большого круга. Фактически, из-за формы земного шара (геоида) длина дуги в 1 угловую минуту изменяется в зависимости от широты, поэтому по соглашению принималась средняя длина 1852 м..
Лье (фр. lieue) старинная французская мера длины. Различали два вида лье: сухопутное 1л=4,444 км, что соответствует 1/25 градуса меридиана.Земли; морское 1л=5,556 км, а это 1/20 градуса меридиана.Земли
Есть версия, что сухопутное лье — это расстояние, которое проходит пешеход за час, а морское — расстояние, которое проходят за час на весельной шлюпке
Астрономические
Астрономическая единица — внесистемная единица расстояния, которая используется в астрономии, составляет ровно 149 597 870 700 м. Это расстояние приблизительно соответствует среднему расстоянию от Земли до Солнца.
Определение и обозначение были приняты во время заседания Международного астрономического союза в Пекине в 2012 году.
Астрономическая единица удобна для определения расстояния между объектами Солнечной системы. Она используется при описании других планетных систем и везде, где есть расстояния сопоставимого порядка, например, в двойных звездных системах.
(
pc
), русское обозначение (пк) — по научному определению это расстояние до определенной точки, у которой годичный тригонометрический параллакс равняется одной угловой секунде. Отсюда и название — «
пар
аллакс» и «
сек
унда».
Простыми словами — парсек это длина катета прямоугольного треугольника, где второй катет равняется одной астрономической единице, а прилежащий угол одной угловой секунде.
Парсек является официальной единицей системы СИ и его точное значение значение 3.08567758 × 1016 метров.
Несколько интересных фактов:
Световой год — единица расстояния, используемая в астрономии. Он равен расстоянию, которое свет преодолевает в вакууме за один юлианский год (365,25 дня, 31,557,600 секунд). В пересчете на другие единицы: 1 световой год = 0,3066 пк = 63241 I = 9,4607 × 1015 м. Оценки обычно предполагают приблизительное значение ≈ 9,5 трлн км. Конвертер длины поможет в сложных вычислениях.