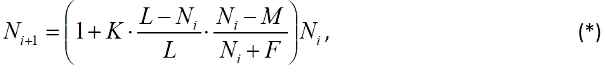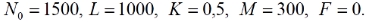Биологи выяснили что для каждого вида животных существует некоторая минимальная численность
Практическая работа № 11
«Саморегуляция»
Файлы-заготовки для выполнения этой практической работы
Файлы-заготовки для выполнения этой практической работы Для выполнения работы откройте файл-заготовку Саморегуляция.xls.
Биологи выяснили, что для каждого вида животных существует некоторая минимальная численность популяции, которая необходима для выживания этой колонии. Это может быть одна пара животных (например, для ондатр) или даже тысячи особей (для американских почтовых голубей). Если количество животных становится меньше этого минимального значения, популяция вымирает. Для этого случая предложена следующая модель изменения численности:
Эта модель отличатся от модели ограниченного роста только дополнительным множителем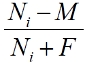 
, где M и F – некоторые числа (параметры), смысл которых вам предстоит выяснить.
1. Выполните моделирование для 30 периодов при следующих значениях параметров модели:
Сравните результаты, которые дают модель классическая модель ограниченного роста и модель (*). Сделайте выводы и опишите, в чём проявляется саморегуляция для этих моделей.
2. Постепенно увеличивая коэффициент F от 0 до 500, выясните с помощью моделирования, как влияет этот коэффициент на саморегуляцию.
3. Через 10 периодов в результате изменения природных условия число животных уменьшилось до 400 (то есть, N10 = 400). Выполните моделирование при этих условиях и опишите, как работает саморегуляция и чем отличается поведение двух сравниваемых моделей.
4. Повторите моделирование п. 3 при N10 = 250 и сделайте аналогичные выводы:
5. Экспериментируя с моделями, найдите минимальную численность популяции Nmin, при которой она выживает в соответствии с моделью (*).
6. Сделайте выводы о смысле коэффициента M в модели (*).
7. Сравните свойства саморегуляции для модели ограниченного роста и модели (*).
Данные Анализ «чтоесли» Подбор параметра
Моделирование
Практические работы
Моделирование популяции животных
Функция «Подбор параметра» в Excel применяется тогда, когда известен результат формулы, но начальный параметр для получения результата неизвестен. Чтобы не подбирать входные значения, используется встроенная команда.
В поле «Установить в ячейке» задаем ссылку на ячейку с расчетной формулой.
Поле «Значение» предназначено для введения желаемого результата формулы.
После нажатия ОК на экране появится окно результата.
Чтобы сохранить, нажимаем ОК или ВВОД.
Ответ:
определите количество животных в состоянии равновесия по результатам моделирования; зависит ли оно от начальной численности?
Ответ:
Моделирование эпидемии
Для выполнения работы откройте файл-заготовку Эпидемия.xls.
При эпидемии гриппа число больных 
изменяется по формуле
,
где 
– количество заболевших в 
-й день, а 
– количество выздоровевших в тот же день. Число заболевших рассчитывается согласно модели ограниченного роста:
,
где 
– общая численность жителей, 
– коэффициент роста и 
– число переболевших (тех, кто уже переболел и выздоровел, и поэтому больше не заболеет):
.
Считается, что в начале эпидемии заболел 1 человек, все заболевшие выздоравливают через 7 дней и больше не болеют.
Выполните моделирование развития эпидемии при 
и 
до того момента, когда количество больных станет равно нулю. Постройте график изменения количества больных.
Ответьте на следующие вопросы:
Сколько человек переболеет, а сколько вообще не заболеет гриппом?
Ответ:
Анализируя результаты моделирования, докажите, что эта модель неадекватна. Какие допущения, на ваш взгляд, были сделаны неверно при разработке этой модели?
Сравните поведение двух моделей при 
, 
и 
. Сделайте выводы.
Модель «хищник-жертва»
Для выполнения работы откройте файл-заготовку ХищникЖертва.xls.
Выполните моделирование биологической системы «щуки-караси»
где 
– численность карасей
– численность щук
при следующих значениях параметров:
– коэффициент прироста карасей;
– предельная численность карасей;
– начальная численность карасей;
– начальная численность щук;
– коэффициент смертности щук без пищи;
и 
– коэффициенты модели.
Постройте на одном поле графики изменения численности карасей и щук в течение 30 периодов моделирования.
Ответьте на следующие вопросы:
Сколько карасей и щук живут в водоеме в состоянии равновесия?
Ответ:
Что влияет на количество рыб в состоянии равновесия: начальная численность хищников и жертв или значения коэффициентов модели?
Ответ:
Практическая работа № 10а.
Модель «две популяции»
Для выполнения работы откройте файл-заготовку ДвеПопуляции.xls.
Белки и бурундуки живут в одном лесу и едят примерно одно и то же (конкурируют за пищу). Модель, описывающая изменение численности двух популяций, имеет вид:
Здесь и 
– численность белок и бурундуков; 
и 
– их максимальные численности; 
и 
– коэффициенты прироста; 
и 
– коэффициенты взаимного влияния.
Объясните, на основании каких предположений была построена эта модель.
Выполните моделирование изменения численности двух популяций в течение 15 периодов при 
, 
, 
, 
, 
и 
. Постройте графики изменения численности обеих популяций на одном поле.
Ответьте на следующие вопросы:
Является ли эта модель системной? Почему?
Ответ:
Какова численность белок и бурундуков в состоянии равновесия?
Ответ:
Саморегуляция
Для выполнения работы откройте файл-заготовку Саморегуляция.xls.
Биологи выяснили, что для каждого вида животных существует некоторая минимальная численность популяции, которая необходима для выживания этой колонии. Это может быть одна пара животных (например, для ондатр) или даже тысячи особей (для американских почтовых голубей). Если количество животных становится меньше этого минимального значения, популяция вымирает. Для этого случая предложена следующая модель изменения численности:
, (*)
Сравните результаты, которые дают модель классическая модель ограниченного роста и модель (*). Сделайте выводы и опишите, в чём проявляется саморегуляция для этих моделей.
Моделирование работы банка
, 
, 
, 
.
крутой. Практика Моделирование. Кредит xls. Уровень A
Моделирование
Математическое моделирование
где S – сумма кредита, i – годовая процентная ставка кредита, делённая на 12; n – число месяцев, в течение которых нужно выплатить кредит.
Используя электронную таблицу или программу на языке программирования, определите, сколько всего денег выплатит дядя Ваня банку по процентам (сверх 100 тыс. рублей).
Какова в этом случае будет величина ежемесячной выплаты:
Какова в этом случае будет общая сумма выплат:
p1 = 100000 : 12 = 8333,33 р.
Вторая часть, p2, зависит от номера месяца k, поэтому будем обозначать её как p2k. Она вычисляется как оставшаяся сумма основного долга, умноженная на годовую процентную ставку кредита, делённую на 12:
Например, в первый месяц выплат 
(выплат ещё не было), поэтому
Во второй месяц оставшаяся сумма долга равна
S1 = 100000 – 8333,33 = 91666,67 р.
При этом получается другая выплата по процентам:
Постройте график выплат дяди Вани при дифференцированных платежах. Сколько всего денег он переплатит по процентам?
Ответ:
Какой способ выплат выгоднее для дяди Вани:
Какова в этом случае будет общая сумма выплат:
Моделирование развития популяции
Моделирование эпидемии
Для выполнения работы откройте файл-заготовку Эпидемия.xls.
При эпидемии гриппа число больных 
изменяется по формуле
,
где 
– количество заболевших в 
-й день, а 
– количество выздоровевших в тот же день. Число заболевших рассчитывается согласно модели ограниченного роста:
,
где 
– общая численность жителей, 
– коэффициент роста и 
– число переболевших (тех, кто уже переболел и выздоровел, и поэтому больше не заболеет):
.
Считается, что в начале эпидемии заболел 1 человек, все заболевшие выздоравливают через 7 дней и больше не болеют.
Выполните моделирование развития эпидемии при 
и 
до того момента, когда количество больных станет равно нулю. Постройте график изменения количества больных.
Ответьте на следующие вопросы:
Сколько человек переболеет, а сколько вообще не заболеет гриппом?
Ответ:
Анализируя результаты моделирования, докажите, что эта модель неадекватна. Какие допущения, на ваш взгляд, были сделаны неверно при разработке этой модели?
Сравните поведение двух моделей при 
, 
и 
. Сделайте выводы.
Модель «хищник-жертва»
Для выполнения работы откройте файл-заготовку ХищникЖертва.xls.
Выполните моделирование биологической системы «щуки-караси»
где 
– численность карасей
– численность щук
при следующих значениях параметров:
– коэффициент прироста карасей;
– предельная численность карасей;
– начальная численность карасей;
– начальная численность щук;
– коэффициент смертности щук без пищи;
и 
– коэффициенты модели.
Постройте на одном поле графики изменения численности карасей и щук в течение 30 периодов моделирования.
Ответьте на следующие вопросы:
Сколько карасей и щук живут в водоеме в состоянии равновесия?
Ответ:
Что влияет на количество рыб в состоянии равновесия: начальная численность хищников и жертв или значения коэффициентов модели?
Ответ:
Саморегуляция
Для выполнения работы откройте файл-заготовку Саморегуляция.xls.
Биологи выяснили, что для каждого вида животных существует некоторая минимальная численность популяции, которая необходима для выживания этой колонии. Это может быть одна пара животных (например, для ондатр) или даже тысячи особей (для американских почтовых голубей). Если количество животных становится меньше этого минимального значения, популяция вымирает. Для этого случая предложена следующая модель изменения численности:
, (*)
Сравните результаты, которые дают модель классическая модель ограниченного роста и модель (*). Сделайте выводы и опишите, в чём проявляется саморегуляция для этих моделей.
Моделирование Практические работы Моделирование популяции животных
Моделирование
Практические работы
Моделирование популяции животных
Функция «Подбор параметра» в Excel применяется тогда, когда известен результат формулы, но начальный параметр для получения результата неизвестен. Чтобы не подбирать входные значения, используется встроенная команда.
В поле «Установить в ячейке» задаем ссылку на ячейку с расчетной формулой.
Поле «Значение» предназначено для введения желаемого результата формулы.
После нажатия ОК на экране появится окно результата.
Чтобы сохранить, нажимаем ОК или ВВОД.
Ответ:
определите количество животных в состоянии равновесия по результатам моделирования; зависит ли оно от начальной численности?
Ответ:
Моделирование эпидемии
Для выполнения работы откройте файл-заготовку Эпидемия.xls.
При эпидемии гриппа число больных 
изменяется по формуле
,
где 
– количество заболевших в 
-й день, а 
– количество выздоровевших в тот же день. Число заболевших рассчитывается согласно модели ограниченного роста:
,
где 
– общая численность жителей, 
– коэффициент роста и 
– число переболевших (тех, кто уже переболел и выздоровел, и поэтому больше не заболеет):
.
Считается, что в начале эпидемии заболел 1 человек, все заболевшие выздоравливают через 7 дней и больше не болеют.
Выполните моделирование развития эпидемии при 
и 
до того момента, когда количество больных станет равно нулю. Постройте график изменения количества больных.
Ответьте на следующие вопросы:
Сколько человек переболеет, а сколько вообще не заболеет гриппом?
Ответ:
Анализируя результаты моделирования, докажите, что эта модель неадекватна. Какие допущения, на ваш взгляд, были сделаны неверно при разработке этой модели?
Сравните поведение двух моделей при 
, 
и 
. Сделайте выводы.
Модель «хищник-жертва»
Для выполнения работы откройте файл-заготовку ХищникЖертва.xls.
Выполните моделирование биологической системы «щуки-караси»
где 
– численность карасей
– численность щук
при следующих значениях параметров:
– коэффициент прироста карасей;
– предельная численность карасей;
– начальная численность карасей;
– начальная численность щук;
– коэффициент смертности щук без пищи;
и 
– коэффициенты модели.
Постройте на одном поле графики изменения численности карасей и щук в течение 30 периодов моделирования.
Ответьте на следующие вопросы:
Сколько карасей и щук живут в водоеме в состоянии равновесия?
Ответ:
Что влияет на количество рыб в состоянии равновесия: начальная численность хищников и жертв или значения коэффициентов модели?
Ответ:
Практическая работа № 10а.
Модель «две популяции»
Для выполнения работы откройте файл-заготовку ДвеПопуляции.xls.
Белки и бурундуки живут в одном лесу и едят примерно одно и то же (конкурируют за пищу). Модель, описывающая изменение численности двух популяций, имеет вид:
Здесь и 
– численность белок и бурундуков; 
и 
– их максимальные численности; 
и 
– коэффициенты прироста; 
и 
– коэффициенты взаимного влияния.
Объясните, на основании каких предположений была построена эта модель.
Выполните моделирование изменения численности двух популяций в течение 15 периодов при 
, 
, 
, 
, 
и 
. Постройте графики изменения численности обеих популяций на одном поле.
Ответьте на следующие вопросы:
Является ли эта модель системной? Почему?
Ответ:
Какова численность белок и бурундуков в состоянии равновесия?
Ответ:
Саморегуляция
Для выполнения работы откройте файл-заготовку Саморегуляция.xls.
Биологи выяснили, что для каждого вида животных существует некоторая минимальная численность популяции, которая необходима для выживания этой колонии. Это может быть одна пара животных (например, для ондатр) или даже тысячи особей (для американских почтовых голубей). Если количество животных становится меньше этого минимального значения, популяция вымирает. Для этого случая предложена следующая модель изменения численности:
, (*)
Сравните результаты, которые дают модель классическая модель ограниченного роста и модель (*). Сделайте выводы и опишите, в чём проявляется саморегуляция для этих моделей.
Моделирование работы банка
, 
, 
, 
.