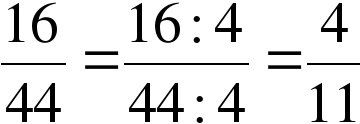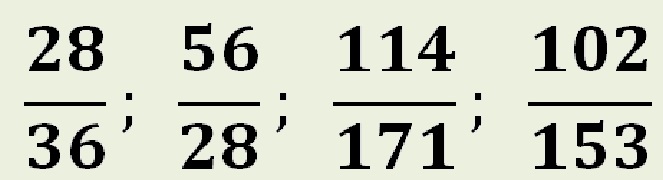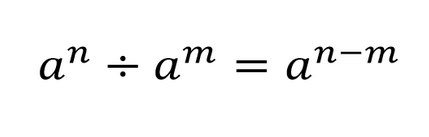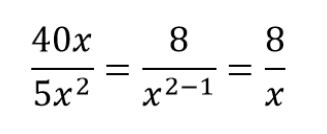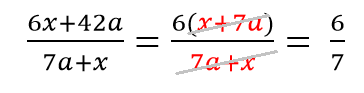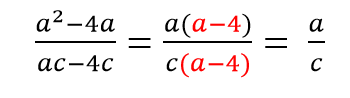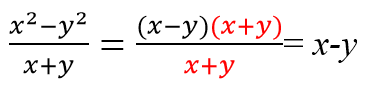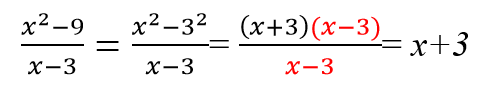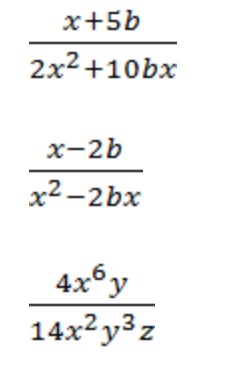Как упростить десятичную дробь
Как упростить десятичную дробь до наименьшей возможной дроби?
5 ответов
Я хочу упростить дробь в своем приложении. Дробь похожа на x/y, где x и y-целые числа. Я хочу упростить дробь до ее простейшей формы. Может ли кто-нибудь дать мне советы, как это сделать? Заранее спасибо.
Я попытался написать алгоритм, чтобы упростить десятичную дробь до дроби, и понял, что это не слишком просто. Удивительно, но я посмотрел в интернете и все коды, которые я нашел, были либо слишком длинными, либо не работали в некоторых случаях. Еще больше раздражало то, что они не работали для.
Алгоритм непрерывной дроби производит только уменьшенные дроби (номинатор и знаменатель относительно просты), и дроби в некотором смысле являются «best rational approximations» к заданному действительному числу.
Я не являюсь человеком JavaScript (обычно программирую в C), но я попытался реализовать алгоритм со следующей функцией JavaScript. Пожалуйста, простите меня, если есть глупые ошибки. Но я проверил функцию, и она, кажется, работает правильно.
Примеры (с числом итераций while-loop):
Вот пример различных уточнений:
Попробуйте вместо этого эту программу:
Тогда вы можете использовать его следующим образом:
Вы можете посмотреть демо-версию здесь: http://jsfiddle.net/MZaK9/1/
Каков наилучший способ получить десятичную дробь в позиции n из поплавка (вырезав из числа все, кроме этой десятичной дроби)? Это должно работать так: getDecimal(3.654987, 4) => returns 0.0009 getDecimal(3.654987, 2) => returns 0.05
Я пытаюсь создать довольно простое приложение для калькулятора. У меня возникла проблема с десятичными дробями. Я довольно новичок в C#,, так что на самом деле не знаю, что здесь делать. Когда я нажимаю на кнопку десятичной дроби в своем калькуляторе, я хочу, чтобы он проверил число в textbox и.
с одной стороны, но
(точно, т. е. это целое число) с другой стороны.
Теперь вы можете использовать алгоритм Евклида, чтобы получить gcd и разделить его, чтобы получить уменьшенную долю.
Я просто возился с кодом и сам получил ответ:
На случай, если кому-то это понадобится.
P.S: Я не пытаюсь показать свой опыт или диапазон знаний. На самом деле я провел много времени в JSFiddle, пытаясь понять это (ну, во всяком случае, не очень долго).
Похожие вопросы:
Как часть приложения калькулятора, я пытаюсь реализовать использование с помощью Сигма-нотации. Однако результат, который он выводит, всегда является десятичным, и rest не имеет значения. Я просто.
В C# округление числа легко: Math.Round(1.23456, 4); // returns 1.2346 Однако я хочу округлить число таким образом, чтобы дробная часть числа округлилась до ближайшей дробной части предопределенной.
В моей базе данных odds хранится в виде дробей (varchar), но мне нужно преобразовать их в десятичные дроби, чтобы позже я мог использовать следующее утверждение select Date, Horse, Racetime.
Я хочу упростить дробь в своем приложении. Дробь похожа на x/y, где x и y-целые числа. Я хочу упростить дробь до ее простейшей формы. Может ли кто-нибудь дать мне советы, как это сделать? Заранее.
Я попытался написать алгоритм, чтобы упростить десятичную дробь до дроби, и понял, что это не слишком просто. Удивительно, но я посмотрел в интернете и все коды, которые я нашел, были либо слишком.
Каков наилучший способ получить десятичную дробь в позиции n из поплавка (вырезав из числа все, кроме этой десятичной дроби)? Это должно работать так: getDecimal(3.654987, 4) => returns 0.0009.
Я пытаюсь создать довольно простое приложение для калькулятора. У меня возникла проблема с десятичными дробями. Я довольно новичок в C#,, так что на самом деле не знаю, что здесь делать. Когда я.
Как преобразовать десятичную дробь в 2 дроби. пример я хочу преобразовать 10.5234 в 10.52 и если дробь равна 0, то дробь и 4.3014 преобразуются в 4.3
Из таблицы T я хочу удалить десятичную дробь из поля varchar ICD10 (буквенно-цифровые коды ICD10), а также сохранить те коды, которые не имеют десятичной дроби. Так что в основном все коды без.
Сокращение дроби.
Мы уже познакомились с основным свойством дроби (см. статью здесь). И знаем, как получить дробь, равную данной. Но сегодня мы поговорим о ДЕЛЕНИИ дроби на одно и то же число.
Деление числителя и знаменателя на одно и то же натуральное число называется СОКРАЩЕНИЕМ ДРОБИ. Но при этом – дроби остаются РАВНЫМИ.
Как сокращать дроби? Будем разбираться.
Итак, сокращение дроби – это действие перехода к новой дроби, равной заданной, но с меньшими числителем и знаменателем. Сокращение дроби выполняют для того, чтобы ее упростить.
Чтобы сократить дробь, нужно разделить числитель и знаменатель дроби на одно и то же натуральное число, которое будет называться общим делителем.
Например, дана дробь 2/6.
На какие числа можно разделить 2? 2 делится на 1, 2. На какие числа можно разделить 6? 6 делится на 1, 2, 3, 6.
Но, мы знаем, что если дробь разделить на 1, то будет та же самая дробь. Поэтому на 1 не сокращают!
Теперь посмотрим на делители чисел 2 и 6. Сравним их:
Найдем одинаковые делители – это только число 2. Значит, мы можем разделить числитель и знаменатель нашей дроби только на 2.
Дробь 1/3 сократить нельзя.
Посмотрим на дробь 16/44. 16 делится на 2, 4, 8, 16. 44 делится на 2, 4, 11, 44. Одинаковые делители – 2, 4.
Разделим дробь на 2 — 16:2/44:2 = 8/22. Эту дробь можно еще сократить на 2. 8/22 = 8:2/22:2 = 4/11. Это очень долго, поэтому будем сокращать сразу на 4.
Дробь 4/11 сократить нельзя.
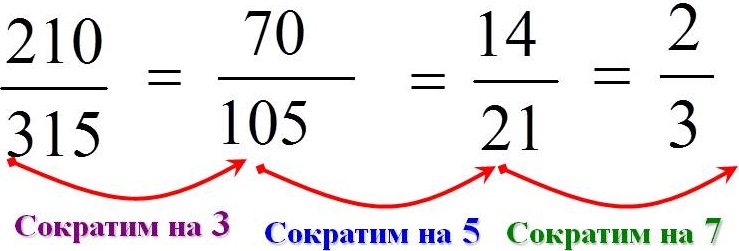
Рассмотрим дробь с большими числами: 210/315.
210 делится на 2, 3, 5, 7, 10, 30, 70, 105, 210.
315 делится на 3, 5, 7, 9, 15, 21, 63, 105, 315.
Общие делители: 3, 5, 7, 105. Будем сокращать дробь постепенно:
Мы видим, что если сокращать поочереди на все общие числители, начиная с меньшего, очень долго. Поэтому для удобства принято сокращать дробь сразу на больший числитель. Т.е. 210/315 = 210:105 / 315:105 = 2/3 Полученную дробь 2/3 сократить нельзя.
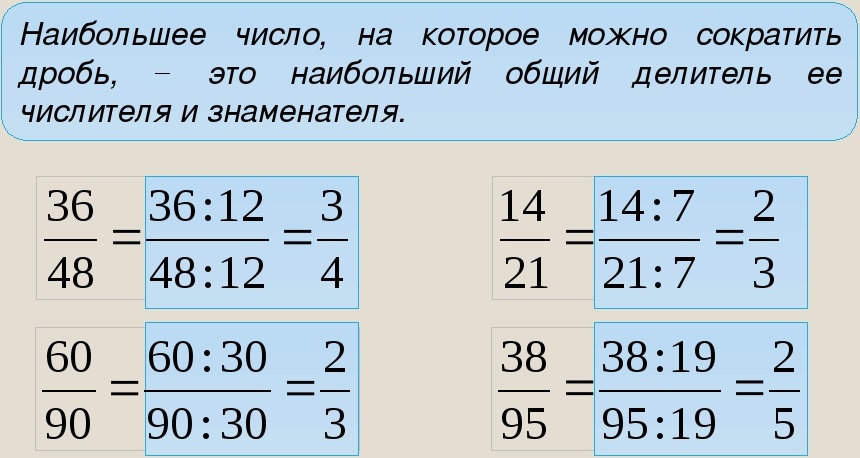
Наибольший общий делитель называют сокращенно — НОД.
Бывают случаи, когда общего делителя нет. Например, у дробей 3/59, 6/31, 11/23 и т.д. Тогда говорят о том, что эти дроби не подлежат сокращению.
Дроби, которые сократить НЕЛЬЗЯ называются НЕСОКРАТИМЫМИ, а числитель и знаменатель называют ВЗАИМНО-ПРОСТЫМИ.
Т.е. наша задача превратить любую дробь в несократимую. Итак, мы познакомились в двумя способами сокращения дробей:
Проверка: 28/36 – наибольший общий делитель (НОД) = 4, значит 28:4/36:4 = 7/9;
56/28 – НОД = 28, значит, 56:28/28:28 = 2/1 = 2;
114/171 – НОД = 57, значит, 114:57/171:57 = 2/3;
102/153 – НОД = 51, значит, 102:51/153:51 = 2/3.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 5 / 5. Количество оценок: 75
Как сокращать алгебраические дроби?
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение
Алгебраическая дробь — это дробь, в числителе и/или знаменателе которой стоят алгебраические выражения (буквенные множители). Вот так:
Алгебраическая дробь содержит буквенные множители и степени.
Необыкновенной алгебраическую дробь делают буквы. Если заменить их на цифры, то карета превратится в тыкву — алгебраическая дробь тут же станет обыкновенной.
Если вы засомневались, что должно быть сверху — числитель или знаменатель — переходите по ссылке и освежите знания по теме обыкновенных дробей.
Сокращение алгебраических дробей
Сократить алгебраическую дробь — значит разделить ее числитель и знаменатель на общий множитель. Общий множитель числителя и знаменателя в алгебраической дроби — многочлен и одночлен.
Если в 7 классе только и разговоров, что об обыкновенных дробях, то 8 класс сокращает исключительно алгебраические дроби.
Сокращение дробей с буквами и степенями проходит в три этапа:
Для сокращения степеней в дробях применяем правило деления степеней с одинаковыми основаниями:
Пример сокращения дроби со степенями и буквами:
Получаем сокращенную дробь.
Запоминаем: сокращать можно только одинаковые буквенные множители. Иными словами, сокращать можно только дроби с одинаковыми буквами.
| ❌ Так нельзя | ✅ Так можно |
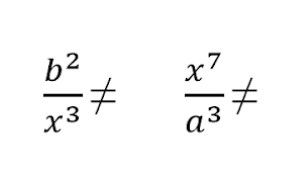 |  |
Примеры сокращения алгебраических дробей с одночленами:
Пример сокращения №1.
Получаем сокращенную алгебраическую дробь.
Пример сокращения №2.
Получаем сокращенную дробь.
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Сокращение алгебраических дробей с многочленами
Чтобы верно сократить алгебраическую дробь с многочленами, придерживайтесь двух главных правил:
Запомните: многочлены в алгебраической дроби находятся в скобках. Между этими скобками вклиниться может только знак умножения. Всем остальным знакам там делать нечего.
Примеры сокращения алгебраических дробей с многочленами:
Последовательно сокращаем: сначала x, затем (x+c), далее сокращаем дробь на 6 (общий множитель).
Сокращаем многочлены a+b (в дроби их 3). Многочлен в числителе стоит в квадрате, поэтому мысленно оставляем его при сокращении.
Вынесение общего множителя при сокращении дробей
При сокращении алгебраических дробей иногда не хватает одинаковых многочленов. Для того, чтобы они появились, вынесите общий множитель за скобки.
Чтобы легко и непринужденно выносить множитель за скобки, пошагово выполняйте 4 правила:
Алгебра не терпит неточность. Всегда проверяйте, верно ли вынесен множитель за скобки — сделать это можно по правилу умножения многочлена на одночлен.
| Для умножения одночлена на многочлен нужно умножить поочередно все члены многочлена на этот одночлен. |
Пример 1.
Пример 2.
Как решаем: выносим общий множитель a за скобки и сокращаем оставшиеся в скобках многочлены.
Сокращение дробей. Формулы сокращенного умножения
Перед формулами сокращенного умножения не устоит ни одна дробь — даже алгебраическая.
Чтобы легко ориентироваться в формулах сокращенного умножения, сохраняйте и заучивайте таблицу. Формулы подскажут вам, как решать алгебраические дроби.
Примеры сокращения дробей с помощью формул сокращенного умножения:
Чтобы раскрыть тему сокращения алгебраических дробей и полностью погрузиться в мир числителей и знаменателей, решите следующие примеры для самопроверки.
Примеры сокращения дробей за 7 и 8 классы
Тема сокращения алгебраических дробей достаточно обширна, и требует к себе особого внимания. Чтобы знания задержалась в голове хотя бы до ЕГЭ, сохраните себе памятку по сокращению дробей. Этот алгоритм поможет не растеряться при встрече с алгебраическими дробями лицом к лицу.
Повторение курса
1. Десятичная дробь – это форма записи обыкновенной дроби, у которой знаменатель равен 10, 100, 1000 и т.д.
Например, 1/100 = 0,01; 7/10 = 0,7 ; 19/1000 = 0,019
2. Запятая в десятичной дроби отделяет:
— целую часть от дробной;
— столько знаков, сколько нулей в знаменателе обыкновенной дроби.
3. Как перевести десятичную дробь в обыкновенную?
Запишите в числитель все число без запятой, а в знаменатель – единицу и столько нулей, столько цифр было отделено запятой в десятичной дроби.
4. Как обыкновенную дробь перевести в десятичную?
1 способ (хорошо работает, когда в знаменателе дроби: 2, 5, 20, 25… и т. д., то есть когда сразу понятно, на что надо умножать): домножить числитель и знаменатель дроби на такое число, чтобы в знаменателе получилось 10, 100, 1000 и т.д., а потом записать результат в десятичном виде.
2 способ: поделить числитель обыкновенной дроби на ее знаменатель (см. раздел сайта: 5 класс/десятичные дроби).
5. Сложение и вычитание десятичных дробей:
Сложение (вычитание) десятичных дробей выполняется так же, как сложение (вычитание) натуральных чисел, в столбик: главное, чтобы запятая во втором числе стояла под запятой в первом. Например:
6. Умножение десятичных дробей (см. раздел сайта: 5 класс/десятичные дроби/умножение десятичных дробей):
Чтобы перемножить две десятичные дроби, нужно умножить их как обычные числа, не обращая внимания на запятые. Потом сложить количество знаков после запятой в первом множителе и во втором множителе, а затем отделить полученное количество знаков в произведении, считая справа налево. Например:
7. Деление десятичных дробей (см. раздел сайта: 5 класс/десятичные дроби/деление десятичных дробей):
Чтобы разделить десятичную дробь на десятичную дробь, надо перенести запятую в делителе вправо на столько позиций, пока он не станет целым. Потом на столько же позиций перенести запятую в делимом. Затем разделить получившиеся числа как обычно, в столбик. При этом в ответе нужно будет не забыть поставить запятую сразу же, как мы «перейдем за запятую» в делимом. Например:
1. Вычислите:
2. Найдите значение выражения:
3. В летнем лагере за смену в 28 дней израсходовали 1 т картофеля. В первые 12 дней расход картофеля составил 38 кг в день. Каким будет расход картофеля в оставшиеся дни, если каждый день он будет одинаковым?
4. Найдите истинные высказывания. Расположите соответствующие им ответы в порядке возрастания, сопоставив их соответствующим буквам, и расшифруйте астрономический термин. Примеры, в которых допущена ошибка, решите правильно и запишите их в тетрадь.
Н 0,25 + 0,5 = 0,3 Б 0,5 * 3 = 0,15 Т 3,6 : 9 = 0,4
О 3,28 + 1,3 = 4,58 И 4 * 1,7 = 6,8 Я 12,3 : 5 = 24,6
Е=40,4 ; Д=36 ; С=8 ; Н=567 ; У=684,18 ; Л=636 ; Б=728 ; И=872.
7. Соком этого растения был отравлен король датский, отец Гамлета. Сейчас оно входит в состав мазей для лечения простуды, бронхита, плеврита, т. к. вещества, входящие в его состав, оказывают спазмолитическое действие. Что это за растение? (Результат каждого действия даёт букву.)
А=842,4 ; К=844,2 ; Е=23,2; С=93,5 ; Е=9,8 ; О=84,24 ; Н=82,124 ; Б=83,244 ; Л=39,244 ; Я=83,2.
8. Этого симпатичного зверька на латыни именовали «королём зелени». Назовите его:
Б=26 ; О=2,06 ; В=2,6 ; И=66,284 ; А=681,38 ; Л=9,08 ; А=9,8 ; Ц=98 ; Н=229,5 ; Е=0,3203 ; Р=22,95 ; К=32,03 ; К=30.
9. Выполните действия и округлите полученный результат с точностью:
Упрощения алгебраических выражений
Что значит упростить алгебраическое выражение
Алгебраическое выражение — одна или несколько алгебраических величин (чисел и переменных), которые объединены с помощью знаков арифметических действий в виде сложения, вычитания, умножения, деления, извлечения корня, возведения в степень (при целых значениях показателей корня и степени), знаков последовательности, определяющих порядок применения данных операций (скобки разного вида).
Обязательным условием для алгебраического выражения является конечное число величин, которые его составляют. Данный принцип пригодиться математикам для решения задач в средних классах школы.
Упростить выражение — это значит уменьшить число арифметических действий, необходимых для вычисления значения данного выражения с учетом определенных значений переменных.
Правила упрощения алгебраических выражений
Существуют основные методы в алгебре для того, чтобы упростить алгебраическое выражение:
В процессе приведения выражения в более простую форму следует использовать полезные советы:
Приведение подобных
Приведение подобных слагаемых в теории заключается в сложении их коэффициентов и приписывании буквенной части.
Подобными являются слагаемые (одночлены), которые обладают буквенной частью.
В выражении 2ab+3ab+b одночлены 2ab и 3ab являются подобными слагаемыми.
Привести подобные — значит, выполнить сложение нескольких подобных слагаемых для получения в результате одного слагаемого.
К примеру, приведем слагаемые:
Заметим, что числа в таких слагаемых умножают на буквы. Данные числа носят названия коэффициентов.
Рассмотрим выражение с квадратной степенью:
Здесь число 3 является коэффициентом.
Разложение на множители
Разложить выражение на множители можно, если вынести общий множитель за скобки, применить формулы сокращенного умножения и другие.
a b 2 + a 2 c = a b 2 + a c
В распространенных случаях разложение на множители следует за приведением подобных при упрощении выражений. В итоге получаются произведения. Чтобы это понять, отдельно нужно упомянуть правила действия с дробями, а именно, при сокращении дроби числитель и знаменатель требуется записать, как произведения.
Сокращение дроби
В процессе сокращения дроби допустимо выполнять умножение или деление числителя и знаменателя дроби на одинаковое число, отличное от нуля, в результате чего величина дроби остается прежней.
Объяснение алгоритм действий при сокращении дробей:
a a + b a 2 = a a + b a · a = a + b a
Важно заметить, что сокращению подлежат исключительно множители.
Озвученное правило является следствием ключевого свойства дроби. Оно состоит в допустимости умножения или деления числителя и знаменателя дроби на одно и то же число, которое не равно нулю. В результате значение дроби останется без изменений.
Существует простой способ, руководствуясь которым можно определить, разложено ли выражение на множители. Арифметическое действие, выполняемое в последнюю очередь при вычислении значения выражения, считается «главным».
Данное правило состоит в том, что, когда при подстановке каких-либо чисел на замену буквам и вычислении значения выражения последнее действие представляет собой умножение, можно заключить, что перед нами произведение, то есть выражение разложено на множители. В том случае, когда на последнем шаге в процессе расчетов выполняется сложение или вычитание, разложение выражения на множители не выполнено, то есть сокращение не допускается.
Сложение и вычитание дробей
При сложении и вычитании обыкновенных дробей требуется найти общий знаменатель, умножить каждую из дробей на недостающий множитель и сложить или вычесть числители:
a b + c d = a · d + c · b b · d ;
Разберем правило на конкретных примерах. Вычислим:
Заметим, что знаменатели являются взаимно простыми, то есть не имеют общих множителей. Таким образом, наименьший общий множитель данных чисел соответствует их произведению. В результате:
В данном случае общим множителем является число 24. Выполним преобразования и упростим выражение:
В данном примере следует смешанные дроби записать в виде неправильных. Далее можно упростить выражение по стандартному алгоритму:
Разберем самостоятельный случай, когда знаменатели не содержат буквы. При этом алгоритм действий такой же, как и при действиях с обыкновенными дробями:
Здесь общий множитель равен 12. Тогда:
a 2 b · 3 4 + a · 2 6 = 3 a 2 b + 2 a 12
Далее можно привести подобные в числители, и разложить на множители при их наличии:
a 2 b 4 + a 6 = 3 a 2 b + 2 a 12 = a 3 a b + 2 12
Когда знаменатели содержат буквы, схема действий существенно не меняется:
Рассмотрим пример, когда требуется упростить выражение:
Разложим знаменатели на множители:
a b 2 = a · b · b a 2 b = a · a · b
Вычислим единые множители:
a b 2 = a ¯ · b ¯ ¯ · b a 2 b = a ¯ · a · b ¯ ¯
Затем можно записать общие множители и выполнить умножение:
a ¯ · b ¯ ¯ · a · b = a 2 b 2
1 a b 2 · a + 1 a 2 b · b = a + b a 2 b 2
Умножение и деление дробей
Умножение и деление дробей выполняют таким образом:
a b · c d = a · c b · d ;
a b : c d = a · d b · c
Арифметические действия выполняют в следующем порядке:
Важно заметить, что при наличии скобок, операции, которые в них заключены, необходимо выполнить в первую очередь. Далее можно приступать к раскрытию скобок. Когда имеется несколько скобок с арифметическими действиями, которые нужно умножить или разделить, в начале проводят вычисления в каждой из скобок, а затем умножение или деление полученных результатов. При наличии внутренних скобок, заключенных в скобки, действия в них выполняют в первую очередь.
Используя правило умножения и деления дробей, получим:
Во многих примерах имеются не только цифры, но и буквы. В этом случае выполняются алгебраические действия, в том числе, приведение подобных, сложение, сокращение дробей и другие операции. Отличия можно заметить при разложении многочленов на множители. Для этого следует пользоваться формулами сокращенного умножения или вынесением единого множителя за скобки.
Ключевой задачей при работе с такими выражениями является запись выражений в виде произведения или частного.
Попробуем упростить выражение:
Так как имеются скобки, следует начать преобразования именно с них. Упростим разность дробей, которая в них записана, чтобы получить вместо нее произведение или частное. Приведем дроби к единому знаменателю и определим сумму:
Заметим, что дальнейшие преобразования не приведут к упрощению данного выражения. Причина этого заключается в том, что каждый из множителей является элементарным. В результате:
Пояснения на примерах
Требуется упростить выражения:
Приведем подобные и упростим выражения:
Заметим, что ab и 2ba являются подобными по той причине, что:
В результате можно сделать вывод, что данные слагаемые обладают одинаковой буквенной частью.
Требуется упростить выражения:
Путем разложения на множители упростим данные выражения:
a b 2 + a 2 c = a b 2 + a c
72 30 = 2 · 2 · 2 · 3 · 3 2 · 3 · 5 = 2 · 2 · 2 · 3 · 3 2 · 3 · 5 = 2 · 2 · 3 5 = 12 5
a a + b a 2 = a a + b a · a = a + b a
В первую очередь выполним разложение на множители:
Дано выражение, которое требуется упростить:
В данном случае требуется разложить знаменатели на множители. Первый знаменатель записан так, что можно вынести за скобки х. Второй знаменатель содержит разность квадратов. Выполним преобразования:
Рассмотрим выражение на наличие общих множителей:
Заметим, что при переносе слагаемых, заключенных в скобках, изменился знак перед дробью. Приведем выражения к единому знаменателю:
Воспользуемся формулой сокращенного умножения, а именно, разностью кубов:
Заметим, что в знаменателе дроби расположено выражение, которое называют неполным квадратом суммы:
x 2 + 2 x + 4 = x 2 + 2 · x + 2 2
Второе по счету слагаемое в неполном квадрате суммы является произведением первого и последнего. Неполный квадрат суммы представляет собой множитель, который входит в состав разложения разности кубов:
Требуется упростить выражения:
Дано выражение, которое требуется упростить:
При наличии в знаменателях одного и того же множителя, возведенного в разные степени, то в общем знаменателе данный множитель будет обладать самой большой из имеющихся степеней. Применительно к этой задаче, общий знаменатель будет состоять из следующих выражений:
a во второй степени;
x в третьей степени;
b в третьей степени;
y в четвертой степени.
В результате получим:
Нужно упростить выражение:
Исключить ошибки можно, если расписать заранее порядок операций. В первую очередь целесообразно суммировать дроби, расположенные в скобках. В результате будет получена только одна дробь. Далее можно приступить к делению дробей. Полученный итог следует прибавить к последней дроби.
Выглядит этот алгоритм таким образом: